一道最值问题的多种解法探究

广东省仁化中学　(512300)

尹杰杰



一道最值问题的多种解法探究

广东省仁化中学(512300)

尹杰杰

A.0B.5C.-10D.10

纵观近年来全国各地的高考试题和模拟试题，我们总可以在试题中找到课本例题和习题的影子．一些高考试题和模拟题来源于课本中例题或者习题的改编，一些高考试题的结论和解题方法也都来源于我们的课本．这是因为课本的例题和习题蕴含着丰富的数学思想和精妙的解题方法，所以课本在我们的高考复习当中占有着举足轻重的地位．这也要求我们教师要引导学生吃透课本中的例题和习题，并能在此基础之上举一反三，灵活变题、解题，进而能让学生达到一题多变和一题多解的能力．下面笔者就从多个视角来思考分析这道模拟试题，揭示这一类试题所考查的知识点.

视角1利用数形结合法求解

图1

评注：解法1是利用线性规划来求解，能让学生更好的理解方程的几何意义，形象生动，直观.学生们大多是运用此方法解答.思路清晰，且过程简单.该方法也是解此类题的一种通法.

双重身份是高等学校在教育资源共享中的一个重要特征，它不仅是共享资源的提供者，也是共享资源的使用者。高校自身是最懂得学校未来的发展状态的，没有哪一个部门比高校自身的管理部门更了解学校的境遇和学校的基础设施以及教育的条件。在对未来高校的发展规划的问题上，高校是最具有话语权的一方。所以学校要跟随时代的脚步，努力争取，充分利用自身的办学自主权，有效规划本校的发展目标以及本校的内部管理活动，特别是在对于教育教学相关活动的决定权上。只有这样，高校才可以在教育资源共享中决定选取学校内部发展何种教育资源作为自身的共享对象，也才有资格自主选择符合自身需要的资源。

图2

评注:解法2首先利用换元法使圆的方程变成我们熟悉的圆心是原点的圆，然后利用线性规划求解，与解法1方法相似，但计算更简单.

解法3：方程x2+y2-2x+4y=0，化简得(x-

图3

设B点的坐标为 (xB,yB)，所以有

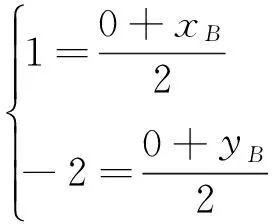
评注:解法3首先求出直线的斜率，发现两直线斜率之积刚好等于-1，故可知在交点处可以求得最值，然后利用圆的对称性求出另一个最值.

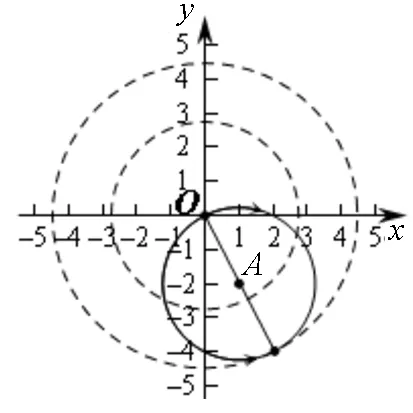
图4

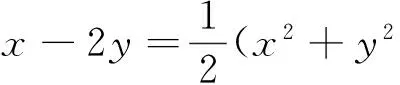
评注：解法4是在观察了方程的特点之后，发现方程的两个一次项系数之比，与所求的问题对应的变量的系数之比相同，然后利用线性规划求解.该解法对学生的能力要求较高，需要仔细发现已知与未知问题在结构上的特点，进而求出问题的结果.

视角2利用代数法求解

解法5令z=x-2y，移项得x=2y+z，代入方程x2+y2-2x+4y=0，化简得5y2+4yz+z2-2z=0.由题意可知该方程一定存在解，所以Δ=-4z2+40z≥0，解得0≤z≤10，故x-2y的最大值是10.

评注:视角2是利用代数法求解，大多数学生都懂得利用此方法作答的.该方法虽然计算量较大，但应用范围广，因此学生一定要熟练掌握.

视角3利用三角函数法求解

评注:视角3是利用三角函数法求解，首先把方程化为圆的参数方程，然后利用三角函数自身的范围来求解问题的最值，该方法过程简洁，计算量小，构思巧妙，是一种很好的解题工具.故学生一定要熟练掌握，这样也可以大大节省做题的时间.

视角4利用柯西不等式求解

解法7：方程化简为(x-1)2+(y+2)2=5，由柯西不等式得：[12+(-2)2][(x-1)2+(y+2)2]≥[1·(x-1)+(-2)·(y+2)]2.所以25≥(x-2y-5)2，两边开平方得5≥x-2y-5≥-5，故10≥x-2y≥0.所以x-2y的最大值为10.

评注:视角4是利用选修中的柯西不等式求解.首先看到所求式子的系数有1和-2，然后想到柯西不等式的结构特点，就知道构造12和(-2)2就可以构造出柯西不等式.大多数学生都没有很好的掌握柯西不等式的应用，故而无法构造出柯西不等式.但是，柯西不等式的解法精妙，往往在高考最后两道大题证明不等式的问题中，利用柯西不等式求解，将会使得问题达到“拨开云雾见天日”的效果，因此对于基础较好的学生，势必要熟练掌握柯西不等式的应用.

视角5利用向量法求解

评注:视角5是利用向量法求解，首先构造了两个向量，使得所求问题的式子等于这两个向量的数量积，然后利用数量积的定义进行求解.该方法较为抽象，学生不容易想到.但是此方法的解题思路简单，也容易掌握，所以学生很有必要掌握此解法.

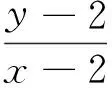
总结：本文通过多视角探讨一道最值问题，如数形结合法，代数法，三角函数法，不等式法等等.不仅能帮助学生巩固基础知识和形成系统的知识网络，而且能帮助学生发散思维，拓宽解题的思路，提高解题的灵活性，进而能很好的培养学生的数学洞察力和解决问题的能力.