坐标变换，一招制胜

江西省临川一中　(344100)

陆继承



坐标变换，一招制胜

江西省临川一中(344100)

陆继承

圆锥曲线作为高考必考内容之一，内容的重要性自然不用多说，其主要培养学生的运算能力，坐标变换及方程思想等.许多圆锥曲线问题，直接处理起来过程繁琐，让许多学生，甚至老师望而却步.本文笔者将通过坐标变换的方式，将一类椭圆问题与圆建立联系，让椭圆问题变得“简单”，达到一招制胜的效果.

先介绍一下平面直角坐标系中的伸缩变换，在人民教育出版社2015年出版的《普通高中课程标准试验教科书数学选修4-4》中对伸缩变换有如下定义：

其应用在三角函数中较多，本文笔者将其在椭圆中的应用作如下阐述.

例1证明：椭圆如下性质：若点M,N是椭圆C上关于原点对称的两点，点P是椭圆上的任意一点，当直线PM,PN的斜率都存在并记为kPM,kPN时，则kPM·kPN是与点P位置无关的定值.

上述过程直接证明，这里笔者想从坐标变换的角度再做分析：

相比之下，坐标变换法证明过程简洁而清楚.又如：

图1

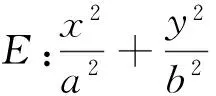
(1)求a,b的值；(2)求证：直线MN的斜率为定值.

通过坐标变换后，复杂的椭圆问题变成了一个简单的圆的问题，处理起来容易多了，可见一招制胜的效果，再如：

(1)求椭圆Γ的标准方程；

①求S1关于k的表达式；

综上，在平时的教学中，特别在第一轮复习时，把“坐标变换”引进圆锥曲线的相关内容中，将极大地提高学生解答这类问题的效率.