由一道高考题引发的思考及探究

山东省聊城大学数学科学学院　(252000)

姜晓洁*　 于兴江



由一道高考题引发的思考及探究

山东省聊城大学数学科学学院(252000)

姜晓洁*于兴江

高考题是经过出卷人反复思考研究而成，凝聚了出卷人的智慧.对高考题进行分析是每一位教师和未来教师必须要做的工作，笔者对2015年高考理科数学全国卷II第20题进行了深刻的分析思考.

1　原题呈现

已知椭圆C:9x2+y2=m2(m>0)，直线l不过原点O且不平行于坐标轴，l与C有两个交点A,B，线段AB的中点为M.

(Ⅰ)证明:直线OM的斜率与l的斜率的乘积为定值；

2　思考探究

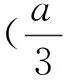
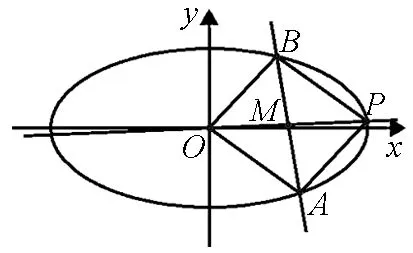
图1

证明法1易知，当直线l的斜率k=0，即l与x轴平行时，或当l与y轴平行时，l过原点等情况下都不能形成平行四边形OAPB.所以可设l:y=kx+b(k≠0,b≠0)，A(x1,y1),B(x2,y2)，M(xM,yM).联立

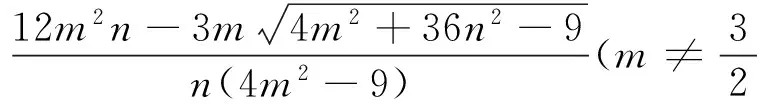
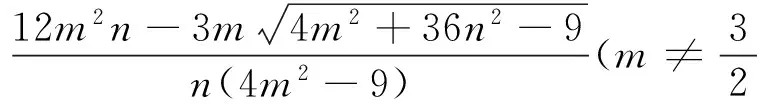
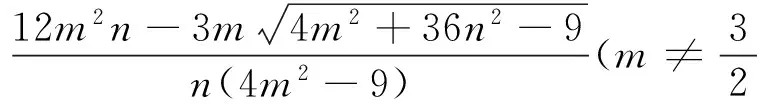
图2

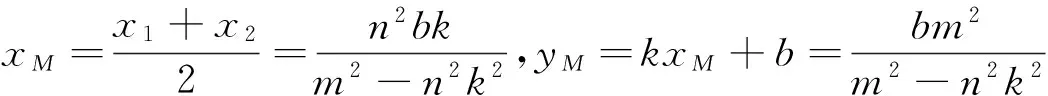
3　反思总结

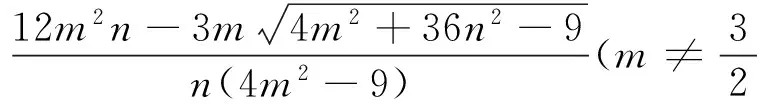
[1]柳俊婷，于兴江，“圆锥曲线的一个性质”再探究[J].中学数学研究(江西)，2015，11.

[2]柳俊婷，于兴江， 2015年山东理科第20题的多解分析及探究[J].中学数学研究(江西)，2015，8.

[3]李静，于兴江.一道高考题的多解及推广[J].中学数学研究(江西)，2013，12.

[4]孙玉英，于兴江.探究 引申 剖析 启示— 一道高考题的赏析[J].中学数学研究(江西)，2013，10.

*作者现为2015级硕士研究生.