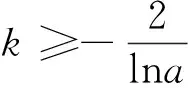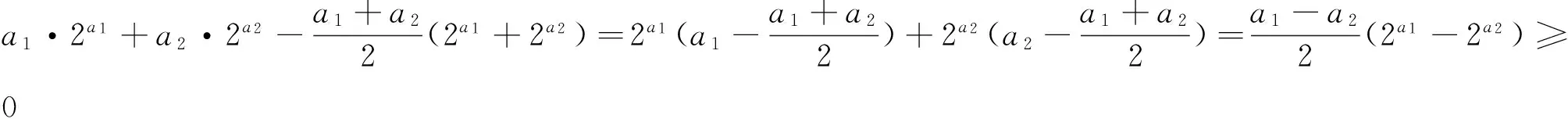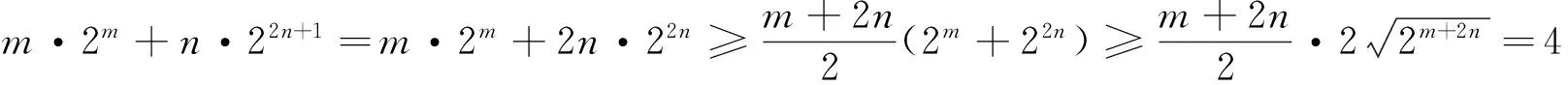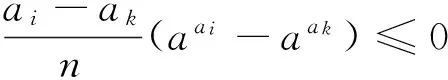一道最值问题的推广、完善与另解
2016-08-26江苏省丹阳高级中学212300
江苏省丹阳高级中学 (212300)
史建军
一道最值问题的推广、完善与另解
江苏省丹阳高级中学(212300)
史建军
1.问题的提出
引例已知m,n∈R,m+2n=2,则m·2m+n·22n+1的最小值为:.
本题是2011年苏、锡、常、镇四市高三第二次模拟考试的填空压轴题,难度较大.但如果仔细观察题中式子的结构特征,发现若令p=2n,则条件式化为m+p=2,目标式化为m·2m+p·2p,由于变量m,p在条件式和目标式中的地位相同,可知当m=p时通常取得某个最值.由m=p=1得m·2m+n·22n+1=4,故最小值为4.
上述解法只是基于代数式特征的“特殊值”法,对于一般情形如何求解?
2.问题的解法及推广、完善
2.1问题的解法及推广
参考答案给出了如下解法:
令g(x)=x·2x+(2-x)22-x(x∈R),∵g(x)=g(2-x),∴g(x)的图像关于直线x=1对称,故求g(x)的最小值只需考虑x∈[1,+∞)的情形.∵g′(x)=2x+x·2xln2-(2-x)22-xln2-22-x=(2x-22-x)+[x·2x-(2-x)22-x]ln2,当x≥1时,x≥2-x,∴2x≥22-x.
(1)若x>2,则(2-x)22-x<0,x·2x-(2-x)22-x>0,∴ln2[x·2x-(2-x)22-x]>0,∴g′(x)>0;
(2)若1≤x≤2,由x≥2-x≥0,∴2x≥22-x,∴x·2x-(2-x)22-x≥0,∴g′(x)≥0;由(1)(2)可得:当x≥1时,g′(x)≥0恒成立,故g(x)在[1,+∞)单调递增,由g(x)图像关于直线x=1对称,g(x)在(-∞,1)单调递减,∴gmin(x)=g(1)=4.因此m·2m+n·22n+1的最小值为4.
上述解法的关键及核心在于构造函数:
g(x)=x·2x+(2-x)22-x,通过研究图像的对称性及函数的单调性进而求得最小值.g(x)结构对称,形式优美,尤其是其图像的对称性及函数单调性让人赏心悦目,解题思路巧妙,结论简明,令人意犹未尽.课后,有学生深入思考后提出了以下结论:
结论1函数g(x)=x·2x+(2k-x)22k-x(k∈R)的图像关于直线x=k对称;
结论2函数g(x)=x·ax+(2k-x)a2k-x(k∈R,a>0且a≠1)的图像关于直线x=k对称;
结论3函数g(x)=x·ax+(2k-x)a2k-x(k∈R,a>0且a≠1).则
当a>1且k>0时,g(x)在(-∞,k)上单调递减,在(k,+∞)上单调递增,故gmin(x)=g(k)=2k·2k.
当0 2.2对推广结论的证明 结论1及结论2的证明很简单,对于结论3,学生给出了如下证明: 证明:当a>1且k>0时,∵g(x)的图像关于直线x=k对称,故求g(x)的最小值只需考虑x∈[k,+∞)的情形.∵g′(x)=(ax-a2k-x)+[xax-(2k-x)a2k-x]lna,当x≥k时,x≥2k-x,又a>1,∴ax≥a2k-x. (1)若x>2k,则(2k-x)a2k-x<0,∴x·ax-(2k-x)a2k-x>0,∴[x·ax-(2k-x)a2k-x]lna>0,∴g′(x)>0; (2)若k≤x≤2k,由x≥2k-x>0,∴ax≥a2k-x,∴x·ax-(2k-x)a2k-x≥0,∴g′(x)≥0;由(1)(2)可得:当x≥k时,g′(x)≥0恒成立,故g(x)在[k,+∞)递增,由g(x)图像关于直线x=k对称,g(x)在(-∞,k)递减,∴gmin(x)=g(k)=2k·ak.当0 当x≤k时,x≤2k-x,又0 上述证明过程及结论无疑是正确的,但学生同时提出:当a>1且k<0以及0 结构如此对称的函数,理应有与结论3完全相同的“完美”结论,但仔细研究结论3的证明过程却发现,上述方法对于a>1且k<0以及0 2.3对结论3的完善 当a>1时, 图1 图2 ㉓T.Austin Lacy,David A.Tandberg,“Rethinking policy diffusion:the interstate spread of‘Finance Innovations’”,Research High Education,2014,55,pp.627 ~649. 图3 当a>1时, 上述结论表明,函数g(x)=x·ax+(2k-x)a2k-x 对于k∈R,当a>1及0 其中“=”当且仅当a1=a2时成立. 观察引例的结构发现,其不过是定理1的特例而已: 其中“=”当且仅当m=2n=1时成立. 上述“=”当且仅当a1=a2=…=an时成立.


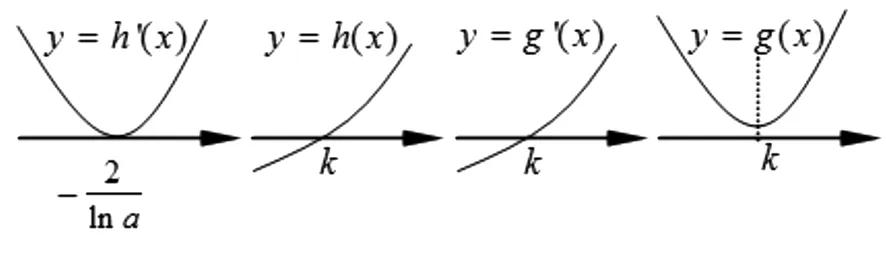




3.对本题解法的进一步研究