“函数与方程思想”在课标卷三角函数中的应用探析

福建省漳州第一中学　(363000)　高国祥福建省漳州第一中学　(363000)

林新建



“函数与方程思想”在课标卷三角函数中的应用探析

福建省漳州第一中学(363000)高国祥福建省漳州第一中学(363000)

林新建

“函数思想”是指运用运动和变化的观点、集合与对应的思想，去分析和研究现实问题或数学问题中的数量关系，建立函数关系，再利用函数的相应性质(定义域、值域、最值、奇偶性、单调性、周期性等)去分析问题、转化问题，从而使问题获得解决.

“方程思想”是指分析数学问题中变量间的等量关系，从而建立方程或方程组，通过解方程或方程组，或者运用方程的性质去分析问题、转化问题，从而使问题获得解决，它是解决各类计算问题的基本思想.

在高考课标卷三角函数试题中，尤其注重对“函数与方程思想”的考查，以此考查学生运用这一思想求解三角函数“最值问题”与“求值问题”的策略和意识.

以下就“函数与方程思想”在课标卷三角函数试题中的应用举例探析，以飨读者.

例1(2011年高考新课标卷Ⅰ理科16题)

分析：本题是三角形问题，已知一边及其对角，无法直接求解，怎么办？

注意到本题是最值问题，若能巧妙引入变量，则可运用正余弦定理建立起待求目标函数关于这个变量的函数，则问题不难获解.

评析：由于“函数思想”的引领，我们引进了变量，从而构造出了待求最值函数关于这个变量的函数，使得问题轻松获解，体现了“函数思想” 在解决最值问题中的重要指导作用.

例2(2015年高考新课标卷Ⅰ理科16题)

在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是.

分析：本题同样无法直接求解，因是取值范围问题，若能引入变量，建立起目标函数关于这个变量的函数，则问题不难获解.

评析：同样是由于“函数思想”的引领，我们引进了变量，从而构造出了待求函数关于这个变量的函数，使得问题轻松获解，体现了“函数思想” 在解决取值范围问题中的重要指导作用.

例3(2010年高考新课标卷Ⅰ理科第11题)

分析：本题也是个最值问题，同样需引入变量，建立起目标函数关于这个变量的函数，问题方能得到解决.

评析：还是由于“函数思想”的引领，我们引进了变量，从而构造出了待求最值函数关于这个变量的函数，使得问题轻松获解，体现了“函数思想” 在解决最值问题中的重要指导作用.

例4(2010年高考新课标卷Ⅰ文科16题)

分析：本题也是三角形问题，无论在哪个三角形中，都是因为条件不够无法直接求解三角形，怎么办？

注意到本题是求值问题，若能将待求变量视为已知，则可运用余弦定理建立起关于这个变量的方程，问题可不难获得解决.

评析：由于“方程思想”的引领，我们得到关于待求变量BD的方程，使得问题轻松获得解决，凸显了“方程思想” 在解决变量求解问题中的重要作用.

例5(2010年高考新课标卷Ⅰ理科16题)

分析：本题也是三角形问题，也因条件不够无法直接求解三角形，怎么办？

同样，因为是求值问题，若能引入变量，建立起关于这个变量的方程，则问题不难获得解决.

评析：在条件不足的情况下，是“方程思想” 引领变量的引入，从而构建出关于待求变量的方程，是问题获得解决的关键之所在，凸显了“方程思想” 在引领变量求解问题中的重要作用.

例6(2013年高考新课标卷Ⅰ理科17题)

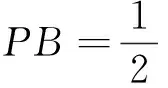
(2)若∠APB=150°，求tan∠PBA.

分析：本题难在第(2)问，同样已知一边及其所对角，无法直接运用正、余弦定理求解，故需引入变量，建立起关于这个变量的方程，问题方能获解.

评析：同样是运用了“方程思想”，我们得到了关于待求变量的方程，从而使问题轻松获解，“方程思想”在求解变量问题中的重要作用不言而喻.