三角形内外角平分线定理在数学解题中的妙用

江西省萍乡市上栗中学　(337009)

肖　锋



三角形内外角平分线定理在数学解题中的妙用

江西省萍乡市上栗中学(337009)

肖锋

三角形内外角平分线性质定理：

三角形的内外角平分线内、外分对边与其延长线所得的两条线段与夹这个角的两边对应成比例.

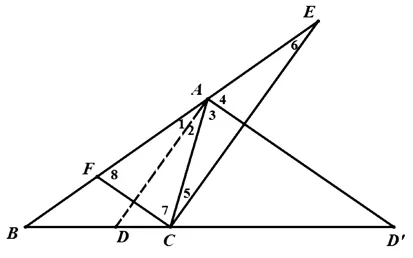
图1

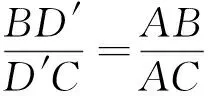
从上述推证过程，我们不难发现，这个定理的逆定理也是成立的，而且AD⊥AD′，不知出于何种原因，这一十分有趣的定理在现行教材中已踪影全无，然而本定理所产生的重要结论，对于目前高中数学解题实践，有着十分重要的作用.

(1)求椭圆的标准方程；

(2)点P是椭圆C上除长轴端点外的任一点，连接PF1,PF2，设∠F1PF2的角平分线PM交C的长轴于点M(m，0)，求m的取值范围.

(3)略.

(2)命题组提供的标准答案，计算十分复杂，现引录如下：

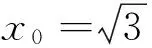
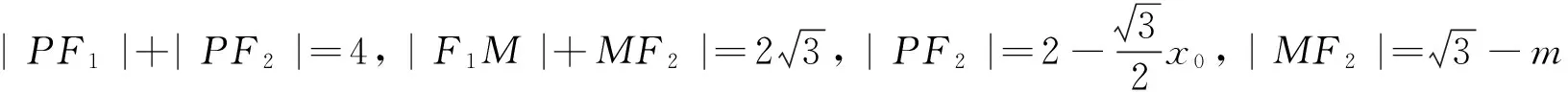
下面我们将其推广到一般情形.

图3

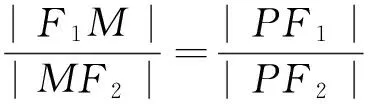
e|PF2|⟹e(a-ex0)=c-m⟹m=e2x0，由x0∈(-a，a)，知m∈(-ae2，ae2)，这里的e表示椭圆的离心率.

循着这个思路，我们来探讨一下双曲线的类似情形.

图4

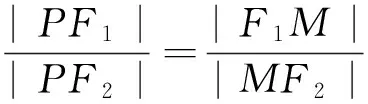
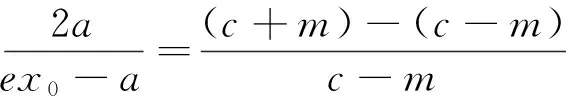
图5

(1) 求实数a的值，并证明PQ与OQ连线的斜率之积是定值；

对于本题的第2问，我们先欣赏一下原创题的标准解法：

由①×③，②×④得

从上述解法可以看到，构思之精巧，运算之难对于一个过分依赖于计算器的当代高中生来说，只能是望而兴叹.下面笔者介绍一种解法，运用三角形内外角平分线性质定理及逆定理，将此题轻松拿下.

上述结论还可以推广到双曲线的一般情形.

值得我们注意的是此类问题对于其它圆锥曲线同样适用.

图6

图7

三角形内外角平分线性质定理，虽然现在初高中教材都不将其列于其中，但由于此定理形式美观，可广泛应用于“折直”比例置换，显然在高中数学解题中有着重要作用，望读者切勿轻视.