引导学生进行反思整理的实践与思考

2016-08-26江苏省苏州实验中学215011

中学数学研究(江西) 2016年8期

关键词：整理解题思维

江苏省苏州实验中学　(215011)

丁益民

引导学生进行反思整理的实践与思考

江苏省苏州实验中学(215011)

丁益民

现代学习观指出：学生的学习是一种选择性学习，是一种实践性学习，是一种创新性学习.从本质上看，学生的数学学习过程是一个自主构建自我理解数学知识的过程，即在自己原有的知识背景、活动经验和理解的基础上进行学习活动，并通过自己的主动活动，包括独立思考、与他人交流和自我反思等，主动地去进行数学的建构与理解.在这样的过程中，获得经验、对经验的分析与理解、对获得过程以及活动方式的反思至关重要，但实际教学中学生的“反思”不够，“整理”不多，原因出在我们教师不敢或不愿给学生“反思”的机会，反而用大量重复的“题海”训练耗尽了学生自主反思整理的时间，殊不知，没有反思的学习过程必定是低效甚或无效的.

在近一年的教学实践中，笔者在任教班级(我校为江苏省四星级高中，学生为我校高一年级最好生源，学生基础扎实，数学水平较高)进行“优秀生”的反思整理的指导实践，根据学生自身的学习情况进行适当的反思整理，整理学习过程中的学习心得，反思学习过程中的经验体会，一年的尝试与探索，得到了一些收获与启示，本文试借一些案例谈谈具体的做法与思考.[注：部分作业的文字表述和篇幅笔者作了适当的调整与完善]

一、反思整理认知误区，弄清错误的前因后果

在某一知识点学习过程中，学生的认知进程并非一帆风顺，有时会出现认知错误，特别是知识建构的初始阶段，如不及时引导学生进行反思，将影响学生对知识的准确理解，并且这样的认知隐患还可能影响与之相关问题的处理.通过反思整理，可让学生认识到原有认知错误的根源，同时整理出正确的理解方式，为今后的“再学习”提供有理有据的学习材料.

案例1高一潘智康同学在学习不等式内容进行了如下整理：

问题已知实数-1≤m-n≤1，1≤m+n≤3，求m+2n的范围.

错解：因为-1≤m-n≤1，1≤m+n≤3，所以0≤m≤2，0≤n≤2，即0≤2n≤4，故0≤m+2n≤6.

分析：错解在于单纯地把m，n进行分离重组，没有意识到他们的内在联系，它们是互相牵制的.

图1

图2

在学习过线性规划知识后，可以作出平面区域解释这样做“范围扩大”了，以图2为证：

从图中明显可见，四边形DEFG区域的是它原本表示的区域，而四边形OABC区域则是运算后的区域，显然“扩大”了，值得警惕!

正解：1°、待定系数法

设m+2n=x(m-n)+y(m+n)，可得

2°、换元法

3°、线性规划法

记S=m+2n，变形为m=S-2n，可知目标函数的两个最优解为(0，1)，(2，1)，即Smax=1，Smax=5，即1≤m+2n≤5.

图3

总结：以上几种方法有一个共同点，就是整体化，这样就不产生多余的运算以致扩大范围.

相比来看，待定系数法与换元法可行性更高，而线性规划法要画图，比较复杂，一旦画不准还会影响结果.

这是一份对自己认知错误进行完整的反思整理作业，既有错解暴露，又有错因分析，既有正解展示，又有方法比较，将原有认知错误的前因后果总结得清清楚楚，学生对相关知识理解的深度必然不是局限在方法层面了，而是将认知的触角上升至理性分析的高度，这正是学习数学的本真之道.

二、反思整理认知视角，逐步建立起完备的认知观念

学生的认知过程是一个循序渐进、螺旋上升的过程，而认知观念的建立则更是长期的系统建构过程，在不断的渗透与长期的训练中，经常引导学生进行相关问题认知视角的反思整理，有可能让学生建立起完备的认知系统．

案例2 高一周明浩同学在解决以下“平面几何”问题后，历时近半个月，多次和笔者、同学探讨，经过多次的反思后整理而成：

问题在△ABC中，已知AB=AC=6，AD=4，且△ABC的外心在BD上，求BC的长度.

这是一道平面几何问题，之前在课上学到：几何问题可从多个角度研究.

回忆：在学习“正(余)弦定理”时，老师让我们从多个角度研究解三角形问题，主要有：正余弦定理知识、坐标法(解析法)、向量法、纯几何方法.下面也从这四个角度来解决该问题：

整理1：正(余)弦定理知识(老师课堂讲的方法)

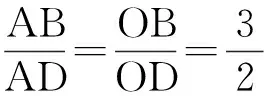
在△ABD与△ABC中分别由余弦定理得

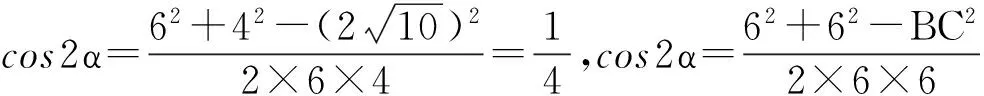
点评：本法是课本中的基本模型(苏教版必修5第10页例2，第16页例6)，其中蕴含的“算二次”数学思想体现得淋漓尽致，值得拥有！关注课本，重视数学思想方法是今后学习的重中之重！

整理2：坐标法(自己课后的思考方法)

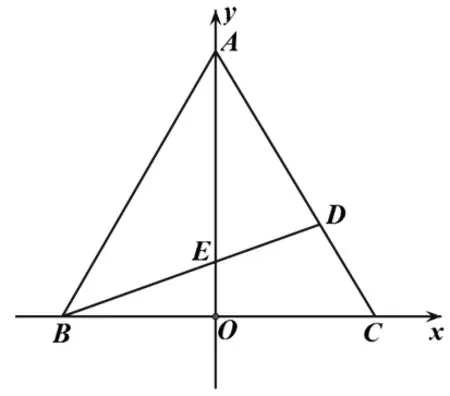
图4

在Rt△ABO中，由勾股定理得m2+n2=36(2)

点评：显而易见，坐标法处理本题的优势是不涉及“角”，容易想到，运算不难，关键是要大胆去“设点”，另外，其中又一次运用了“算两次”的数学思想也值得关注.

整理3：向量法(与老师交流后的想法)

图5

点评：向量法的精髓在于“向量关系数量化”，其中两组三点共线又看到了“算两次”数学思想的影子，此法相对于其他方法似乎运算量较大，相对而言，有点笨重.

整理4：纯几何方法(与同学相互研讨后而得)

图6

点评：几何法难想，尤其是辅助线不容易想到，对我们的要求比较高，但在和几位同学的讨论后，还是能够接受这样的“挑战”，可作为上述方法的“锦上添花”之作.

这样的反思整理，真心为学生的毅力和钻研精神点赞，也越发说明只要我们给学生充分的反思时间，给予他们适当的点拨与指导，他们是可以将课堂中的“研究”延续到课后的“反思”中去.他们在反思整理中有对课堂听课内容的“整理”，有自己与同学、老师交流后的“反思”，加上教师的点评，学生对问题的认识可上升为知识框架下的系统认识.这样的反思整理实为一份学习成果汇报，与老师互动，与同学合作，学习的过程是真实的、互动的，更重要的是学生在此过程中建立了良好的认知观念(几何问题可从哪些角度去研究)，感受到核心数学思想的价值(“算两次”思想的多次体会)，而这些都将有利于学生建立起完备的认知观念.

三、反思整理思维过程，“二次”反思优化思维结构

学习的过程也是学生逐步调整和优化的过程，他们在解决一些问题时，最初的思维线路并非清晰简洁，甚或是繁杂无章.通过老师的讲评与指导，思维线路有了明显的改进或改变.若在此基础上再与同学探究讨论，与老师交流(包括书面交流)，查阅相关资料等，再对已有的思维线路进行改进与调整，直至形成较为清晰顺畅的思维结构，这对学生的思维训练的个体性是很有效的.

案例3高一俞婷同学对一道试题的思维方式的反思整理

题目设α∈R，若x>0时，均有[(a-1)x-1](x2-ax-1)≥0(①)，则实数a=_________.

图7

最初想法：对于①式，如果用因式分解会得到

笔者在批阅该作业时评注：本例可否从其他角度入手？比如函数的图像.

几日后，学生进行了“二次”整理：

换一种思路：用函数图像来研究

图8

老师，本题是否还有其他比较好的解法？盼告知.

笔者思考后慎重地给学生再次做了引导性的交流批注：

这个不等式的主变量是哪个？具有任意性的变量可否从特殊值上思考？试试看.

次日，学生再次整理道：这是一道关于变量x的不等式恒成立的问题，而且最后结果是一个确定的值，可选用特殊值来逼出a的值：

当x=1时，有(a-2)(0-a)≥0，可得0≤a≤2.

感受：尽管没有求出a的值，但缩小了范围，离目标近了.

感受：意料之外的结果，但又是情理之中，特殊值发挥了很多的作用.

学生在反思整理作业中完全真实地暴露了研究问题的思维过程：从一开始的茫然(思维受阻)到教师点拨后的切换角度研究问题(思维转换)，再主动与老师交流后的反思整理，最后根据问题的特点巧妙迅速解决了问题(思维变通).整个反思整理的过程中学生经历的何止是思维过程的优化呢？这恰是历练了做学问的“三重”境界，由此获得的情感、态度和价值观层面的深刻体悟是难以磨灭的.

四、反思整理解题经验，个性总结印象深刻

学习需要总结反思，尤其是解题活动中，解题失败或错误是普遍现象，关键是要引导学生学会总结反思，提取出相关解题经验作为后续学习的基础.在总结时，有时抽象晦涩的文字语言无法表达出对解题经验的学习体会，我们可以给学生充分的自由度，指导学生自己根据自身情况选用符合他们认知理解的方式进行总结，让其自由发挥，进行自我表征，印象自然深刻.

案例4高一李康同学擅长打油诗，在其整理作业中常见打油诗式的总结性反思.

案例4.1在订正不等式恒成立习题后，他用如下“打油诗”加以总结：