用对立统一观点探索圆锥曲线的发展——谈圆锥曲线焦点弦的又一个优美性质

江苏省盱眙中学　(211700)

严曼丽



用对立统一观点探索圆锥曲线的发展
——谈圆锥曲线焦点弦的又一个优美性质

江苏省盱眙中学(211700)

严曼丽

我国现代诗人艾青有下面一首赞美光的诗篇：我们从千万次的蒙蔽中觉醒,我们从千万种愚弄中学会了聪明.统一中有矛盾,前进中有逆转,动力中有助力，革命中有背叛.甚至光中也有暗,暗中也有光,不少丑恶与自私隐藏在光的下面.此首诗核心讲了一个对立统一的观点.唯物辩证法认为任何事物都是对立统一的矛盾的统一体,对立中有统一,统一中有对立,矛盾着的对立统一相互协调，相互促进,促成事物的发展.

三大圆锥曲线,从唯物辩证法的角度看是相互对立的,但又是相互统一的.他们有一个统一定义,这是统一性.同时又有各自的特殊性,这又是对立的.根据唯物辩证法,三大圆锥曲线的性质很多情况下是同时出现的,同时李成波[1], 陈广权[2],邹书生[3]也都给出很多统一的性质,证明了这一事实.本文中，笔者对圆锥曲线焦点弦的性质作了一些研究,得到圆锥曲线焦点弦的又一个性质,现写成下文,以供大家参考.

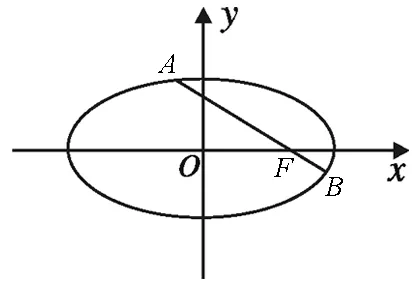
图1

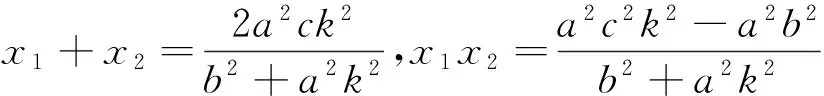
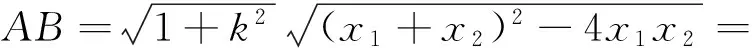
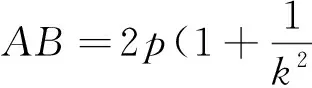
证明:同引理1.当k不存在时AB=2p.

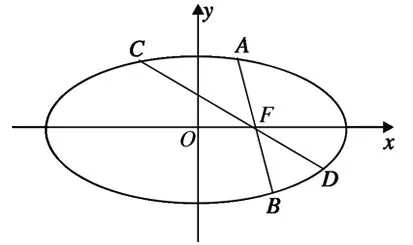
图2

证明：如图2，∵AB，CD是椭圆C1的焦点弦,由引理1得

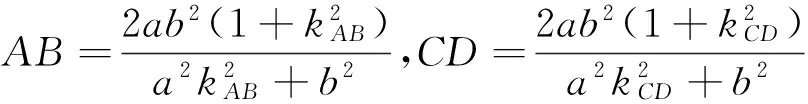
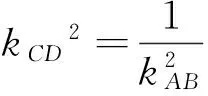
图3

注:定理1中,如果AB，CD分别是过左焦点和右焦点的弦，即如图3所示,也有同样的结论.

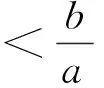
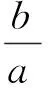
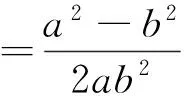
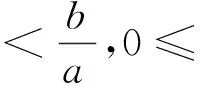
根据引理3，类似定理1，把椭圆改为抛物线也有类似的性质,证明留给读者自行解决,此处不再赘述.

圆锥曲线向前发展的步伐还将继续,我们坚信三大圆锥曲线还有很多类似的性质,笔者也将在这条道路上继续摸索.

[1]李成波.求离心率的一组美妙结论[J].中学数学杂志,2010,7,32-33.

[2]陈广权.圆锥曲线又一有趣性质[J].数学通讯,2011，1，23-24.

[3]邹书生.圆锥曲线与定比有关的一个性质[J].数学通讯,2009,6,32-33.