一道三角不等式引发的思考

江苏省扬州市甘泉小学　(225000)

赵元翔*



一道三角不等式引发的思考

江苏省扬州市甘泉小学(225000)

赵元翔*

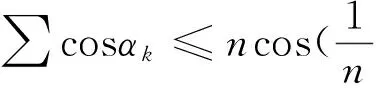
基于上述不等式的研究，笔者发现以下三个定理：

(第1次放缩后还有2n-1项，并且每项

(第2次放缩后还有2n-2项)≤…≤

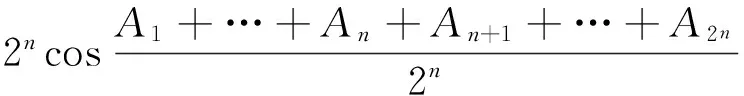
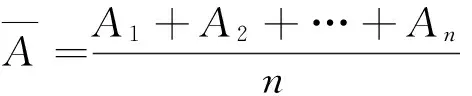
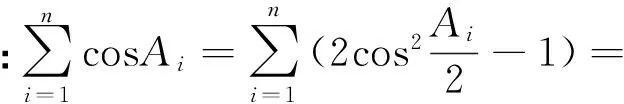
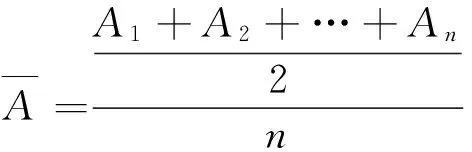
注：定理2和定理3的上界没有直接的大小关系.

例1在凸六边形中A1A2A3A4A5A6中，cosA1+cosA2+…+cosA6≤0.

笔者在拜读《控制不等式基础》一书时发现，控制不等式和三角函数不等式有着精妙的联系，并从中得到了几个有意义的结论，能很容易地证明并推广一些三角不等式.

控制不等式[3]对于x=(x1，…，xn)∈Rn，把x的分量排成递减的次序后记作x↓=(x[1]，…，x[n])，即x[1]≥…≥x[n]；把x的分量排成递增的次序后记作x↑=(x(1)，…，x(n))，即x(1)≤…≤x(n).

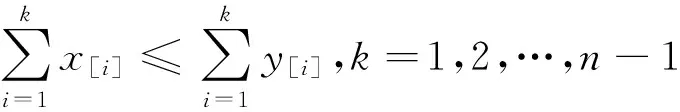
定理4[3]设x，y∈In，则

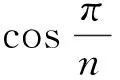
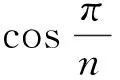
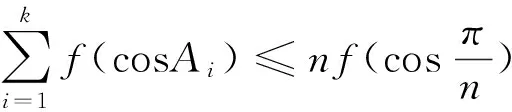
仿照上面的证明，结合定理2容易知道：

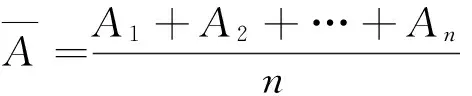
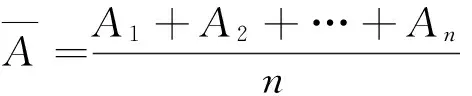
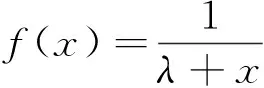
[1]匡继昌.常用不等式[M].山东科学技术出版社(第四版), 2010.

[2]杨学枝.数学奥林匹克不等式研究[M].哈尔滨工业大学出版社, 2009.

[3]王伯英.控制不等式基础[M].北京师范大学出版社, 1990.

[4]严心悦.一个猜想不等式的姊妹形式[J].中学数学研究(江西),2015,10:25-26.

* 作者为扬州市首批免费师范生.