千淘万漉虽辛苦，吹尽狂沙始到金——由一道高考压轴题所引发的探究

安徽省凤阳县临淮中学　(233100)

张琳　刘祖权



千淘万漉虽辛苦，吹尽狂沙始到金
——由一道高考压轴题所引发的探究

安徽省凤阳县临淮中学(233100)

张琳刘祖权

下课铃刚响，笔者走下讲台步履疲惫地进入办公室，一位爱钻牛角尖的男生带着数学问题紧随其后跟进了我的办公室，期望得到我的帮助.

一、问题的出现

题目已知函数f(x)=2x3-3x.

(1)求f(x)在区间[-2,1]上的最大值；

(2)若过点P(1，t)存在3条直线与曲线y=f(x)相切，求t的取值范围；

(3)问过点A(-1,2),B(2,10),C(0，2)分别存在几条直线与曲线y=f(x)相切？(只需写出结论)

这是2014年高考数学北京文科卷中第20题，也是最后一道压轴题，综合性较强，考查知识面广，计算量也较大，相对于文科生来说，确实有一定的难度.笔者边书写计算边画图，最终给出了正确答案，对于如此的解答这位学生并不满意，提出更高要求：“过一点如何判定一元三次函数切线存在的条数，并要求推导一般性的判定方法，给出明确的判断结论”.这着实给我出了难题，对于一般形式的推导而言，不是不能完成，而是心中没底.笔者所顾虑的是由于参数较多，计算量可能较大，判定结论是否简洁适当.就本道压轴题的题干可以觉察出，过一点作三次函数的切线，对切线数存在的判定可能存在着必然的规律.题中第(3)问给出A,B,C三点的具体坐标判断切线数只是问题的一种表象，其背后到底隐藏了什么？带着这个疑问和学生“强加”给的使命，为揭开谜底，笔者决定尝试一下.

二、问题的探究

现在把上述问题一般化：曲线C是一元三次函数f(x)=ax3+bx2+cx+d(a≠0)的图像，过定点P(m，n)作曲线C的切线，推出存在的切线数的判定方法.

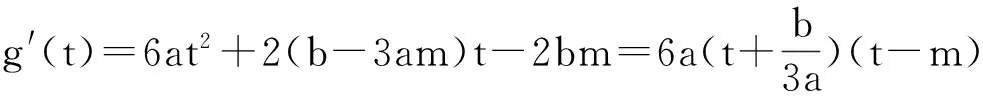
下面分两种情形加以讨论：

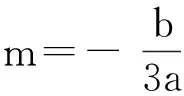
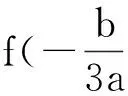
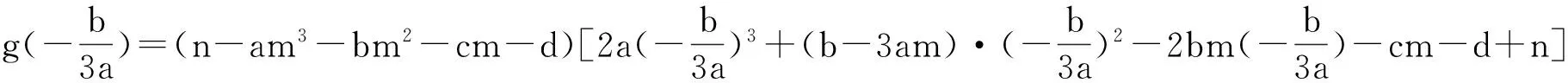
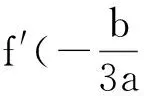
三、探究后的结论

命题曲线C是一元三次函数f(x)=ax3+bx2+cx+d(a≠0)的图像，过定点P(m，n)作曲线C的切线，则曲线C上存在的切线数的判定方法：

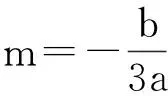
(1)若n<μ或n>λ时，曲线C过点P(m，n)的切线仅有一条；

(2)若n=μ或n=λ时，曲线C过点P(m，n)的切线仅有两条；

(3)若μ

四、回归问题的解答

让我们再来看一道高考压轴题，此题出自于2007年高考数学(理)全国卷Ⅱ第22题：

题目已知函数f(x)=x3-x.

(Ⅰ)求曲线y=f(x)在点M(t，f(t))处的切线方程；

(Ⅱ)设a>0，如果过点(a，b)可以作曲线y=f(x)的三条切线.证明：-a

解析：(Ⅰ)略；(Ⅱ)易知拐点为原点(0，0)，因a>0，所以点(a，b)不是拐点.下面求出拐点函数h(x)=-x，从而有f(a)=a3-a，h(a)=-a，由于a>0，显然f(a)=a3-a>-a，又过点(a，b)可以作曲线y=f(x)的三条切线，所以-a