组合导向浮阀塔板的CFD模拟及反向流分析

刘江琳，张杰旭，纪利俊，陈　葵，武　斌，吴艳阳，朱家文

（华东理工大学化工学院，上海 200237）



组合导向浮阀塔板的CFD模拟及反向流分析

刘江琳，张杰旭，纪利俊，陈葵，武斌，吴艳阳，朱家文

（华东理工大学化工学院，上海 200237）

精馏塔板上的气液两相流动对传质效率有重要影响。根据实验数据拟合得到平均气含率关联式，将其加入动量源项，采用Fluent软件对1.2 m直径的组合导向浮阀塔板上的气液两相流动进行CFD模拟，考察了塔板上的气液两相流动状况。清液层高度的模拟结果与实验数据关联式相吻合，验证了模拟的正确性。对塔板上液相的非理想流动进行了分析，通过对反向流进行量化和统计计算出反向流体积分数（即反向流体积占塔板总体积的百分比）。3块不同浮阀排布塔板的反向流体积分数时均值的计算结果表明，梯形浮阀和矩形浮阀的排布方式对反向流影响很大，通过合理排布能够使工业塔板的反向流体积分数时均值从22.0%下降到19.4%，降幅达到11.8%。本研究结果可望对塔板的设计和优化提供指导。

气液两相流；计算流体力学；组合导向浮阀；反向流；优化

DOI：10.11949/j.issn.0438-1157.20151376

引　言

精馏塔是重要的分离液体混合物的设备，广泛应用于炼油、化工、制药、环保等行业。为提高板式精馏塔的处理量和板效率，研究人员几十年来一直致力于开发大通量和高传质效率的新型塔板。在正常的操作负荷下，增大处理量往往需要更大的塔径。然而，随着塔径的增大，塔板两侧弓形区及降液管附近的滞留区和回流区增大，板上的非理想流动增多，使传质效率下降［1-2］。塔径的增大还会增加塔板液相的流程长度，导致塔板上液面落差增大，使得塔板上气液接触和流动的非均匀程度增加，对传质效率产生不利影响。为降低液面落差，减缓常规大直径塔板上由于滞流和回流等引起的返混问题，新型塔板如林德筛板［3］、ADV微分浮阀塔板［4］、导向浮阀塔板［5］等具有优良流体力学性能的塔板相继被开发并投入实际应用。

导向浮阀塔板由Lu等［5］开发，其特点是在矩形浮阀上设有适当大小的导向孔，开口方向与液流方向一致，可降低甚至消除液面梯度，并减少液体的返混程度。组合导向浮阀塔板［6-7］是在矩形导向浮阀塔板基础上的改进，相比矩形导向浮阀，梯形导向浮阀具有更强的导向作用，通过梯形浮阀和矩形浮阀的适当排列，组合导向浮阀的流体力学性能比单一矩形导向浮阀更优，对减少塔板上液体滞留区和回流区而降低板上液位差更为有效。两种浮阀结构如图1所示。

图1　矩形浮阀和梯形浮阀结构Fig.1　Structure diagram of rectangular directed valve and trapezoidal directed valve

正常操作条件下，板上液相的反向流和滞流等非理想流动是造成液相返混的主要原因。现有研究表明塔板上的液相返混对板效率影响很大。虽然回流区的反向流使该位置点效率上升，但由于回流区流量小、所占面积大，回流液相沿着传质推动力的“逆方向”流动，总体上使板效率明显下降［8］。塔板上气液接触产生相界面的过程也是造成液相返混的重要因素，气液湍动程度增大，一方面加快了传质速率，另一方面使塔板上的返混程度增加。气液湍动程度与塔内气液负荷大小、气液接触方式、塔板结构和体系性质等密切相关［9-10］，其对板效率的影响还未有一致的结论。板上液相的非理想流动可以通过实验进行考察，如采用示踪剂测定停留时间分布（RTD）和速度分布［2，11］以及热膜流速仪测定流场［10］等。

与传统的通过实验测定压降、RTD、流场等方法相比，计算流体力学（CFD）的应用使分析塔内两相流动的能力大幅提升，已经成功地用于筛板塔［12-13］、浮阀塔［14-15］等塔板的气液两相流动特性的研究。然而现有文献中的CFD模拟多通过气液相分数图和速度矢量图等从表观上解释和说明两相的流动行为，对于塔板结构变化、操作条件变化对板上非理想流动影响的研究较少，特别是缺乏对模拟结果的数据进行统计和分析。本文将拟合得到的平均气含率关联式加入动量源项MG，L中，通过自定义函数（UDF）加载到Fluent 6.3中，模拟并分析1.2 m塔径的工业组合导向浮阀塔板上的气液两相流动特性，根据模拟结果对反向流进行了量化和统计，分析了矩形浮阀和梯形浮阀的排布方式对反向流体积分数的影响，研究结果可望对今后的工业塔板设计和优化提供指导。

1　数学模型与参数设定

1.1数学模型

塔板为气液两相进行传质的场所，板上的液体受到气体搅动，形成极其复杂的两相流动。大直径塔板上还存在滞留区和回流区，增加了研究板上流体力学的难度。双欧拉模型假设两种湍流流体在时间上共存，可视为互相穿透的连续介质，其运动规律遵从各自的控制微分方程，并且两种流体间存在动量、能量以及质量的相互作用，亦即相间耦合。相比拟单相模型和混合模型，双欧拉模型对两相间作用的描述更为全面具体，更加符合精馏塔板上气液两相的实际流动状况［12，15］。本研究的模拟基于双欧拉模型，湍流模型采用标准k-ε模型。文献［13，15-16］已对标准k-ε模型应用于精馏塔板的CFD模拟进行了详细描述，此处不再叙述。模拟所用的主要方程组见表1。

1.2网格划分及参数设定

本文模拟的组合导向浮阀塔板的结构和尺寸取自实际的工业塔板，塔径1.2 m，板间距0.45 m，堰高0.054 m，升气孔面积与塔总截面之比为10.3%，降液管底隙高度为0.015 m，浮阀最大开度为0.015 m，导向孔高度为0.005 m。根据塔板的对称性，只取一半塔板进行模拟，以节省计算量。网格的划分对计算结果的正确性和计算成本的大小有重要影响，在靠近塔板壁面处，考虑到浮阀结构较为复杂，进行了加密处理。以清液层高度［16-17］为判别标准验证了网格独立性。随着网格数目的增多，模拟值与实验值越接近，当划分网格数目超过639383时计算值与实验值相当接近，此时再增加网格数变化趋势平缓。考虑到网格数越多计算成本越高，最终塔板底部采用8 mm非结构四面体网格划分，在上方区域采用12 mm结构六面体网格，共计网格639383个。塔板边界条件及网格划分如图2所示。

表1　R模型方程Table 1　Model equations

采用空气-水系统模拟了浮阀全开条件下板上气液两相流场，模拟工况参数：液流强度Lw=10～40 m3·m-1·h-1，阀孔动能因子F0=7.57（m·s-1）·（kg·m-3）0.5，堰高hw=0.044～0.074 m。时间项采用隐格式，对流项采用一阶迎风格式，压力-速度耦合方程选用相间耦合的Simple方法，计算精度为10-3。液相体积分数初值设为0.5，时间步长为0.002 s。

图2　模拟的边界条件及网格划分Fig.2　Boundary conditions and grid map of simulation

2　结果与讨论

2.1清液层高度

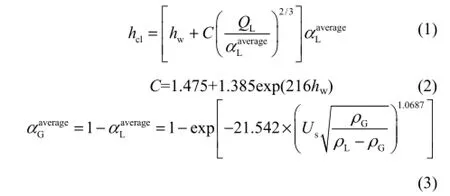
将式（3）代入表1中动量源相MG，L公式中，通过UDF加载到Fluent中进行模拟。计算过程中监测清液层高度的变化，当清液层高度在6 s时间内保持不变即认为计算收敛。

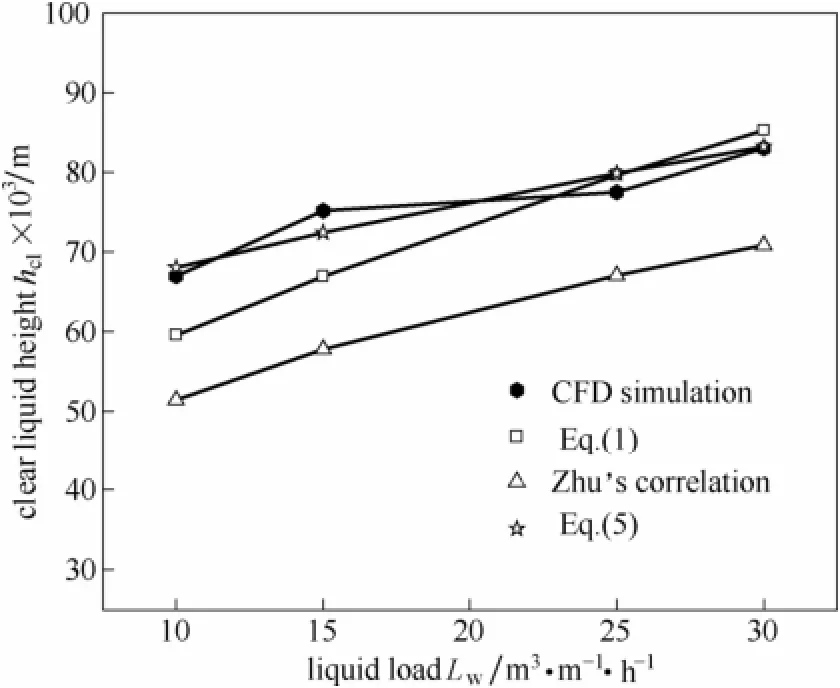
图3　清液层高度随液流强度的变化Fig.3　Clear liquid height as a function of liquid loadF0=7.57 （m·s-1）·（kg·m-3）0.5，hw=0.054 m

图4　清液层高度随堰高的变化Fig.4　Clear liquid height as a function of weir height［F0=7.57 （m·s-1）·（kg·m-3）0.5，Lw=20 m3·m-1·h-1］

由图3和图4可以看出，在阀孔动能因子和堰高不变的条件下，清液层高度随液流强度增大而增加，本研究关联式［式（1）］、朱艳等［21］的关联式以及关联式式（5）［22］与CFD模拟值的平均相对误差分别为6.9%、18.6%、2.2%；在阀孔动能因子和液流强度不变的条件下，清液层高度随堰高增高而增加，关联式式（1）、朱艳等［21］的关联式以及关联式式（5）［22］与CFD模拟值的平均相对误差分别为10.2%、 10.1%，9.1%。对比其他文献中清液层高度模拟值与实验值的误差，文献［14］的平均相对误差为4.4%，文献［13］的平均相对误差为10.0%，文献［15］的平均相对误差为23.8%，文献［12］的平均相对误差为43.6%。本研究的清液层高度的模拟结果随液流强度及堰高的变化趋势与实验结果一致，模拟结果的误差范围适中，因此本研究的模拟结果是可信的。

2.2流场分析

图5给出了清液层高度在x方向（即液相主体流动方向）的模拟结果，可以看出液层高度沿主体流动方向总体为下降趋势并呈现一定波动，液位差的存在加之气相传递的动量使液体克服阻力向前流动。同一位置不同时刻的清液层高度有微小的变化，但总体上的变化趋势一致。Getye等［16］在塔径1.22 m筛板塔的CFD模拟中发现，板上气相速度和液相速度沿x方向发生周期性变化，造成清液层高度呈现周期性波动，波谷出现在开孔处。在图5中可以看出类似的现象，出现波谷之处是浮阀导向孔所在的位置，此时大量气体从导向孔喷出，具有很大的动量，推动液相向x方向流动，从而导致导向孔处液层急剧下降，液相在板上流动过程中途经多个导向浮阀，使得清液层高度呈现周期性波动。

图5　清液层高度沿x方向的变化Fig.5　Clear liquid height profiles along x direction［F0=7.57 （m·s-1）·（kg·m-3）0.5， hw=0.054 m，Lw=20 m3·m-1·h-1］

不同时刻气相分数前视图和不同液层高度俯视图的模拟结果分别见图6和图7。由图可知塔板上气液两相流动是从非稳态到稳态的瞬态变化过程，在t =6 s后塔板上气含率基本不变，计算达到了动态平衡。塔板上的两相空间可以分为液相连续区、中间过渡区、气相连续区。在近塔板处，液相是连续相，气相是分散相，随着塔板高度的增加液相体积分数逐渐减小。在中间过渡区，气液两相之间没有明显的分界面。在气相连续区，液相迅速减少，气相占据了主导地位。

图6　不同时刻y =0 mm截面的瞬态模拟结果Fig. 6　Snapshots of front view at y =0 mm ［F0=7.57 （m·s-1）·（kg·m-3）0.5， hw=0.054 m， Lw=20 m3·m-1·h-1］

图7　不同高度相含率分布Fig.7　Gas hold-up profile at different elevations［F0=7.57 （m·s-1）·（kg·m-3）0.5， hw=0.054 m， Lw=20 m3·m-1·h-1］

图8为z =0.01 m液相速度矢量图及梯形浮阀和矩形浮阀的局部流场放大图。可以发现在塔板的弓形区和溢流堰附近存在明显的反向流，在浮阀四周也存在少量的反向流。从图8的局部流场对比中可以发现，矩形浮阀两侧喷出气体的方向较混乱，大部分气体的流动方向与液相主体流动方向（x方向）近似垂直，少量气体逆液流或顺液流方向喷射，总体上对液相在主体流动方向上的推动作用是微弱的，因此矩形浮阀的导向作用主要依靠导向孔。而梯形浮阀气体多从沿浮阀两侧梯形形状的斜边法向方向喷出，喷出气体的速度与x方向存在8°～62°的夹角，气体速度在x方向上的分量对液体有推动作用。模拟结果验证了梯形浮阀具有比矩形浮阀更强的导向作用。

2.3浮阀排布对液相反向流的影响

前文已述塔板结构对板上气液两相流动影响很大。相比气相，板上液相的非理想流动对板效率的影响更为显著［23］。目前，在组合导向浮阀塔的设计上，矩形和梯形两种浮阀的数量及排布位置多凭经验。为了优化浮阀的排布，本研究通过反向流的体积分数表征液相返混程度。根据工业塔板的结构设计了3块不同浮阀排布方式的塔板：a、b、c。其中a塔板是前文模拟所用的工业塔板。这3块塔板上的浮阀数量和浮阀中心在塔板上的位置相同，区别在于其第3排两个梯形浮阀的排布位置不同。各塔板上两种浮阀的具体排布如图9所示。

Liu等［10］通过计算筛板塔的回流区面积分数量化液相返混的程度，结果表明气液相负荷及堰高对反向流面积分数有显著影响。文献［10］给出的只是二维平面上反向流的统计结果，不能全面反映液相在三维空间流动的总体返混情况。此外，该文献模拟的是稳态下的流场，无法描述气液两相剧烈动量交换引起的波动对反向流的影响。本研究根据CFD的模拟结果统计了液相回流体积分数T，以考察液相在三维流动空间上的总体返混情况。

T的计算公式如下

式中，Vxn为x方向液相速度为负的网格体积，αL为液相体积分数，Vtotal为网格总体积。

图8　z =0.01 m截面的液相速度矢量图及梯形浮阀和矩形浮阀的局部放大图Fig.8　Liquid phase velocity vector at plane of z =0.01 m and partial enlarge view of trapezoidal directed valve and rectangular directed valve ［F0=7.57 （m·s-1）·（kg·m-3）0.5，hw=0.054 m， Lw=20 m3·m-1·h-1］

图9　3块不同浮阀排布的塔板结构（实心为梯形浮阀，其余为矩形浮阀）Fig.9　Structure diagram of 3 tray patterns with different valve arrangement （solid patterns represent trapezoidal directed valves， and rest are rectangular directed valves）

本文模拟的是浮阀全开状态下的动态流场，速度矢量随时间变化。对清液层中约22万个网格的液相速度进行统计，根据式（6）计算得到T。为考察动态流场下的反向流体积分数随时间的变化，取模拟达到动态平衡后6 s时间内时间间隔为0.2 s的30个数据点的T，取它们的算术平均值Tav表征液相返混程度。

弓形区、矩形区和整块塔板的T随时间变化的一个计算结果如图10所示。由图可知，板上各区和整块板的T围绕时均值Tav（图中实线）上下波动，符合湍流的随机波动特征。与矩形区相比，弓形区的波动更剧烈，波动范围在时均值的±75.5%，而矩形区的波动范围为时均值的±21.0%。

图10　a塔板的T随时间的变化Fig.10　T of tray a at various time ［F0=7.57（m·s-1）·（kg·m-3）0.5， hw=0.054 m， Lw=20 m3·m-1·h-1］

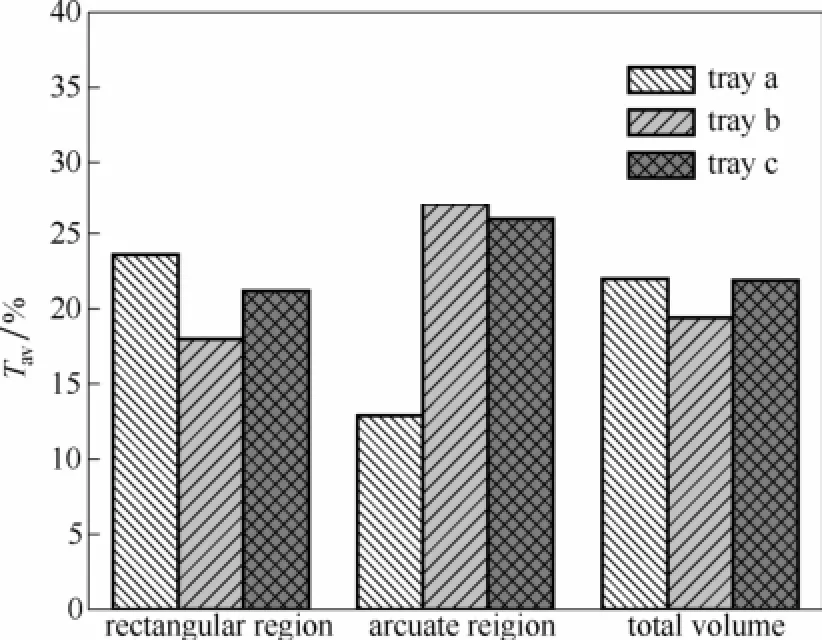
图11　a、b、c塔板的TavFig.11　Tavof trays of a，b and c ［F0=7.57 （m·s-1）·（kg·m-3）0.5，hw=0.054 m， Lw=20 m3·m-1·h-1］

a、b、c塔板的反向流体积分数的时均值Tav的计算结果如图11所示。可以发现第3列浮阀中两个梯形浮阀的排布位置对矩形区和弓形区的Tav都有较大影响，对弓形区的Tav影响更为显著，但弓形区面积只占板上总面积的约1/6，从而使得这3种排布的总体反向流分数差别不如弓形区大。a塔板的排布中两个梯形浮阀都靠近弓形区，使得弓形区的Tav在3种排布中最小，由此可见在弓形区排布梯形浮阀对减少弓形区反向流是非常有效的。a与c的总体的Tav相当。b塔板上总体的Tav值为19.4%，是3种排布中最小的，比实际工业塔板a的22.0%的Tav值低11.8%。这是因为b塔板的浮阀排列方式能够较明显地降低矩形区的Tav，而矩形区面积远大于弓形区面积，使得b塔板上总体的Tav最小。从总体液相返混程度上看，b塔板在这3种排布中最优。

图12　z = 0.02 m截面上典型的x方向液相速度等值线图Fig.12　Liquid velocity contour map in x direction in plane of z = 0.02 m ［F0=7.57（m·s-1）·（kg·m-3）0.5， Lw=20 m3·m-1·h-1，hw=0.054 m］

图13　z = 0.02 m截面上典型的液相速度矢量图Fig.13　Liquid phase velocity vector at plane of z = 0.02 m ［F0=7.57（m·s-1）·（kg·m-3）0.5， Lw=20 m3·m-1·h-1， hw=0.054 m］

图12和图13对比了a和b塔板的x方向液相速度等值线和速度矢量图。由图可知，b塔板在矩形区的反向流少于a塔板，图中圈出的区域中b塔板的反向流很少，而a塔板在该区域的反向流较多。在弓形区中，b塔板的反向流比a塔板多，这与统计结果一致。

以上分析结果表明，不同的浮阀排布方式会产生不同的流场，对反向流影响较大，通过两种浮阀的合理排布可以减少板上液相的返混。本研究结果可望对今后的塔板设计和优化提供指导。

3　结　论

（1）根据实验数据拟合得到平均气含率关联式并加入动量源项MG，L中，模拟了1.2 m工业组合导向浮阀塔板上的气液两相流场，通过清液层高度验证模拟的正确性，结果表明本研究的模拟结果是可信的。

（2）根据模拟结果分析了塔板上气液两相流动特性，并对液相反向流的体积进行了量化统计，以考察液相返混程度。3块不同浮阀排布的塔板的计算结果表明，梯形浮阀和矩形浮阀的不同排布方式对流场及反向流体积有重要影响。通过合理排布，可使工业塔板的反向流体积分数时均值从22.0%下降到19.4%，下降幅度达到11.8%。

符号说明

Ahole——孔面积，m2

C——堰常数

CD——曳力系数

dG——气泡直径，m

E ——液流收缩系数

F0——阀孔动能因子，（m·s-1）·（kg·m-3）0.5

g ——重力加速度，9.81 m·s-2

hap——降液管底隙高度，m

hcl——清液层高度，m

hw——溢流堰高，m

hσ——气泡克服表面张力的压降，m

k ——湍动能，m2·s-2

Lw——液流强度，m3·m-1·h-1

lw——溢流堰长，m

MG，L——动量源相，N·m-3

Nh——孔个数

p ——压力，Pa

Q ——流量，m3·s-1

T ——回流体积分数，%

Tav——回流体积分数的时均值，%

t ——时间，s

Us——空塔气速，m·s-1

u， u ——分别为速度矢量、速度标量，m·s-1

Vslip——气液两相间滑移速度，m·s-1

Vtotal——网格总体积，m3

Vxn——x方向液相速度为负的网格体积，m3

x，y，z ——x、y、z坐标轴，m

α ——相体积分数

αaverage——相平均体积分数

ε ——湍流耗散率，m2·s-3

μeff——有效动力黏度，Pa·s

ρ ——相密度，kg·m-3

σ ——表面张力，N·m-1

下角标

G ——气相

i ——第i个量

L ——液相

q ——气相或液相

References

［1］ PORTER K E， LOCKER M J， LIM C T. The effect of liquid channelling on distillation plate efficiency ［J］. Trans. Inst. Chem. Eng.， 1972， 50（2）： 91-101.

［2］ 余国琮， 黄洁. 大型塔板的模拟与板效率的研究（Ⅰ）： 不均匀速度场的涡流扩散模型 ［J］. 化工学报， 1981， 32（1）： 11-19. YU K T， HUANG J. Simulation and efficiency of large tray（Ⅰ）：Eddy diffusion model with non-uniform liquid velocity field ［J］. Journal of Chemical Industry and Engineering（China）， 1981， 32（1）：11-19.

［3］ 付有成， 王崇智. 板式塔精馏技术进展 ［J］. 石化技术及应用，2000， 18（4）： 231-236. FU Y C， WANG C Z. Progress in rectification technology of tray column ［J］. Petrochemical Technology & Application， 2000， 18（4）：231-236.

［4］ 刘吉， 吕家卓， 谢润兴， 等. 微分浮阀塔板的研究和应用 ［J］. 化学工程， 2000， 28（5）： 10-14. LIU J， LÜ J Z， XIE R X， et al. Study and application on the advanced micro-dispersion valve （ADV） trays ［J］. Chemical Engineering（China）， 2000， 28（5）： 10-14．

［5］ LU X L， LIU X Y， ZHAO P. Directed floating valve trays：CN91215110.2［P］. 1991-11-20.

［6］ 赵培， 李玉安， 张杰旭， 等. 导向浮阀塔板的实验研究 ［J］. 石油炼制与化工， 1998， 29（6）： 14-17. ZHAO P， LI Y A， ZHANG J X， et al. Study on the directed floating valve tray ［J］. Petroleum Process and Petrochemicals， 1998， 29（6）：14-17.

［7］ 李玉安， 赵培， 刘吉， 等. 梯形导向浮阀塔板 ［J］. 高校化学工程学报， 1997， 11（3）： 261-267. LI Y A， ZHAO P， LIU J， et al. Trapezoidal directed valve trays ［J］. Journal of Chemical Engineering of Chinese Universities， 1997，11（3）： 261-267.

［8］ NORILER D， BARROS A A C， MACIEL M R W， et al. Simultaneous momentum， mass， and energy transfer analysis of a distillation sieve tray using CFD techniques： prediction of efficiencies［J］. Ind. Eng. Chem. Res.， 2010， 49（14）： 6599-6611.

［9］ WANG X L， LIU C J， YUAN X G， et al. Computational fluid dynamics simulation of three·dimensional liquid flow and mass transfer on distillation column trays ［J］. Ind. Eng. Chem. Res.， 2004，43（10）： 2556-2567.

［10］ LIU C J， Yuan X G， Yu K T， et al.A fluid-dynamics model for flow pattern on a distillation tray ［J］. Chemical Engineering Science， 2000，55（12）： 2287-2294.

［11］ SOLARI R B， BELL R L. Fluid flow patterns and velocity distribution on commerical-scale sieve trays ［J］. AIChE J.， 1986，32（4）： 640-649.

［12］ KRISHNA R， VAN BATEN J M. CFD simulations of sieve tray hydrodynamics ［J］.Transactions of the Institution of Chemical Engineers. Part A. Chemical Engineering Research & Design， 1999，77（7）： 639-646.

［13］ KRISHNA R， VAN BATEN J M. Modeling sieve tray hydraulics using computational fluid dynamics ［J］. Chemical Engineering Research and Design， 2003， 81（1）： 27-38.

［14］ JIANG S， GAO H， SUN J， et al. Modeling fixed triangular valve tray hydraulics using computational fluid dynamics ［J］. Chemical Engineering & Processing Process Intensification， 2012， 52（2）：74-84.

［15］ LI X G， LIU D X， XU S M， et al. CFD simulation of hydrodynamics of valve tray ［J］. Chemical Engineering & Processing Process Intensification， 2009， 48（1）：145-151.

［16］ GETYE G， NANDAKUMAR K， CHUANG K T. CFD modeling of flow patterns and hydraulics of commercial-scale sieve tray ［J］. AIChE J.， 2003， 49（4）： 910-925.

［17］ 张朦， 张海涛， 张杰旭， 等. 组合导向浮阀塔板多相流的数值模拟［J］. 化学反应工程与工艺， 2015， 31（2）： 106-114. ZHANG M， ZHANG H T， ZHANG J X， et al. Numerical simulation of multiphase flow in combined guided valve tray of distillation column ［J］.Chemical Reaction Engineering and Technology， 2015，31（2）： 106-114.

［18］ BENNETT D L， AGRAWAL R， COOK P J. New pressure dropcorrelation for sieve tray distillation columns ［J］. AIChE J.， 1983，29（3）： 434-442.

［19］ COLWELL C J. Clear liquid height and froth density on sieve trays［J］. Ind. Eng. Chem. Proc. Des.Dev.， 1979， 20： 298-307.

［20］ 张杰旭， 赵培， 李玉安， 等. 组合导向浮阀塔板的开发研究 ［J］.化工进展， 2005， 24（S1）： 69-72. ZHANG J X， ZHAO P， LI Y A， et al. Development and study of combination directed valve trays ［J］. Chemical Industry and Engineering Progress， 2005， 24（S1）： 69-72.

［21］ 朱燕， 熊丹柳， 张秋香. 组合波纹导向浮阀塔板压降的研究 ［J］.化工进展， 2007， 26（S1）： 43-48. ZHU Y， XIONG D L， ZHANG Q X. Research on pressure drop of the combined wave guided valve trays ［J］. Chemical Industry and Engineering Progress， 2007， 26（S1）： 43-48.

［22］ 兰州石油机械所. 现代塔器技术［M］. 2版. 北京： 中国石化出版社，2005： 249. Lanzhou Petroleum Machinery Research Institute. Modern Tower Technology［M］. 2nd ed. Beijing： China Petrochemical Press， 2005：249.

［23］ 邓修， 吴俊生. 化工分离工程［M］. 北京： 科学出版社， 2000： 84-86. DENG X， WU J S. Separation Engineering in Chemical Engineering［M］. Beijing： Science Press， 2000： 84-86.

CFD simulation and backflow analysis of combined directed valve tray

LIU Jianglin， ZHANG Jiexu， JI Lijun， CHEN Kui， WU Bin， WU Yanyang， ZHU Jiawen
（College of Chemical Engineering， East China University of Science and Technology， Shanghai 200237， China）

The flow patterns and hydraulics of gas-liquid flow on a commercial scale distillation tray is of great importance in determining the tray efficiency. Based on experimental data， a new correlation of average gas hold-up was fitted and built in the inter-phase momentum transfer source for CFD simulations. The simulations of combined directed valve trays of 1.2 m air-water system were carried out by Fluent， a commercial CFD software，and the flow pattern characteristics was investigated. The clear liquid height determined from CFD simulations was in good agreement with the predicted results calculated from the correlation in this work， which proved the validity of simulations. Non-ideal flow of liquid phase on the trays was quantified by the backflow volume ratio T，the ratio of backflow volume to total grid volume. The time-averaged values of the backflow volume ratio （Tav） of 3 tray patterns with different arrangements of trapezoidal and rectangular directed valves were calculated respectively. The results showed that the different arrangements of two kinds of valves had remarkable influence on volume fraction of backflow. By reasonable arrangement， Tavcould reduce from 22.0% to 19.4% with the decreased backflow volume by 11.8% compared to the industrial tray. This study was expected to provide a guidance for the tray design and optimization.

gas-liquid flow； CFD； combined directed valve tray； backflow； optimization

date： 2015-10-13.

JI Lijun， jilijun@ecust.edu.cn

TQ 021.1

A

0438—1157（2016）05—1701—09

2015-08-31收到初稿，2015-10-13收到修改稿。

联系人：纪利俊。第一作者：刘江琳（1991—），女，硕士研究生。