再谈数学知识在生物学解题中的应用
2016-08-21祝远超
祝远超
(湖北省天门市岳口高级中学 431702)
生物学是一门基础学科。它与很多学科都有着直接或间接的联系。因此,在解答生物学试题的过程中有时必须应用相关学科的知识,特别是数学。
1 排列组合在生物学解题中的应用
例1 (用排列组合求杂交后代基因型和表型的种类数及某种个体占的比例):已知A与a、B与b、C与c 3对等位基因自由组合,基因型分别为AaBbCc、AabbCc的两个个体进行杂交。下列关于杂交后代的推测,正确的是( )。
A.基因型有18种,AaBbCc个体占的比例为1/16
B.基因型有12种,aaBbcc个体占的比例为1/16
C.表现型有6种,Aabbcc个体占的比例为1/8
D.表现型有8种,aaBbCc个体占的比例为1/16
解析:解答此类试题的方法较多,如棋盘法、分枝法等,但最简单的方法莫过于分解组合法,即先求每对基因杂交的结果,然后将其自由组合,如下:
Aa×Aa→1/4AA、1/2Aa、1/4aa,即3种基因型,2种表型;Bb×bb→1/2Bb、1/2bb,即2种基因型,2种表型;Cc×Cc→1/4CC、1/2Cc、1/4cc,即3种基因型,2种表型。据排列组合的知识可得,杂交后代基因型的种类数为3×2×3=18种,表型的种类数为2×2×2=8种,故B、C均错。杂交后代中AaBbCc占的比例为1/2×1/2×1/2=1/8,aaBbCc占的比例为1/4×1/2×1/2=1/16,参考答案:D。
针对性训练1:基因型分别为ddEeFf和DdEeff的两个个体进行杂交,在3对等位基因各自独立遗传的条件下,下列关于杂交后代的推测,正确的是( )。
A.基因型有8种,ddEeFf个体占的比例为1/8
B.基因型有12种,DdEeff个体占的比例为1/8
C.表现型有6种,DdEeFf个体占的比例为1/16
D.表现型有8种,ddEeff个体占的比例为1/16
参考答案:B。
例2 (用排列组合计算食物链的条数):图示某生态系统中食物网的图解,其中食物链的条数是( )。

A.6 B.7 C.8 D.9
解析:由图可知,蜘蛛有2种食物(甲虫和叶状虫),蜥蜴只有一种天敌(蛇)。由排列组合的知识可知,同时含有蜘蛛和蜥蜴的食物链条数为2×1=2条,同理可得:同时含有蜘蛛和知更鸟的食物链条数为2×2=4条,同时含有叶状虫和蜜雀的食物链条数为1×2=2条,故下图中食物链的条数为2+4+2=8。参考答案:C。
点拨:①上述方法不仅用到了排列组合知识,还用到了一种重要的方法——“捆绑法”,即分别将蜘蛛和蜥蜴、蜘蛛和知更鸟、叶状虫和蜜雀“捆绑”在一起;②此法与常规方法——逐条计数法(一条一条地数)相比,不仅简单、快捷,而且准确率较高(稍微仔细一点,一般不会出错)。
思维警示:用“捆绑法”计算食物链的条数时,不同“捆绑”对象之间均不能有捕食关系,如上述蜥蜴、知更鸟、蜜雀两两之间均无捕食关系。
针对性训练2:图示一个草原生态系统的营养结构,则该食物网包含了( )条食物链。

A. 10 B. 11 C. 12 D. 13
解析:由图可知,放养的牲畜有两种食物和一种天敌,由排列组合的知识可知,含有放养的牲畜的食物链有2×1=2条,同理可得,含有兔的食物链有2×2=4条,含有鼠的食物链有2×2=4条,含有食草昆虫的食物链分别有2×1=2条,故图中共有2+4+4+2=12条食物链,参考答案:C。
例3 (用排列组合计算DNA分子中碱基的排列顺序数):由50个脱氧核苷酸构成的双链DNA分子,按其碱基对的排列顺序不同,可分为多少种( )。
A.504B.450C.425D.254
解析:由题意可知,该DNA分子含有25个碱基对(或脱氧核苷酸对),其中每个碱基对都有A-T或T-A或C-G或G-C 4种可能。由排列组合的知识可知,其碱基对的排列顺序数为4×4×……4(共25个4相乘)=425。参考答案:C。
点拨:①若一个DNA分子中含有n个碱基对(或脱氧核苷酸对),则其碱基对的排列顺序数最多有4n种;②若是单链DNA分子,则n代表单链中的碱基(或脱氧核苷酸)的数目。
思维警示:①4n是理论上的最大值;②若题中告诉了(或能求出)DNA分子中各种碱基(或碱基对)的具体数目,则结果不能用4n表示。
针对性训练3:含有2000个碱基的双链DNA分子,其每条链上的碱基排列方式最多有( )种。
A.42000B.41000C.22000D.21000
参考答案:B。
例4 (用排列组合归纳探究性实验预期结果的种类):现有一种植物种子,已知其萌发受水分、温度和氧气的影响,但不知其萌发是否与光有关。现欲探究光对该种子萌发的影响,请依据实验的方法步骤,预测可能的实验结果,并分析得出相应的结论。
材料和用品:数量充足的铺有滤纸的培养皿、无菌水、表面消毒过的种子等。
方法步骤:①向培养皿中倒入适量的水,将等量的种子分别放入A、B两组培养皿中;②将A组置于有光照的环境中,B组置于黑暗环境中,在培养过程中,使两组所处温度、水分、空气状况等相同,且适宜。
请写出可能的实验结果及相应的结论:
解析:A组种子可能萌发(A1),也可能不萌发(A2),B组种子可能萌发(B1),也可能不萌发(B2)。将其自由组合,结果为:①若A组萌发,B组也萌发(A1、B1),则光对该种植物种子的萌发无影响;②若A组萌发,B组不萌发(A1、B2),则光是该种植物种子萌发的必要条件之一;③若A组不萌发,B组萌发(A2、B1),则光抑制该种植物种子的萌发。
理论上还有第4种可能:若A组不萌发,B组也不萌发(A2、B2),但它不符合生物学原理,应舍弃,故应只写上述3种情况。
2 函数知识在生物学解题中的应用
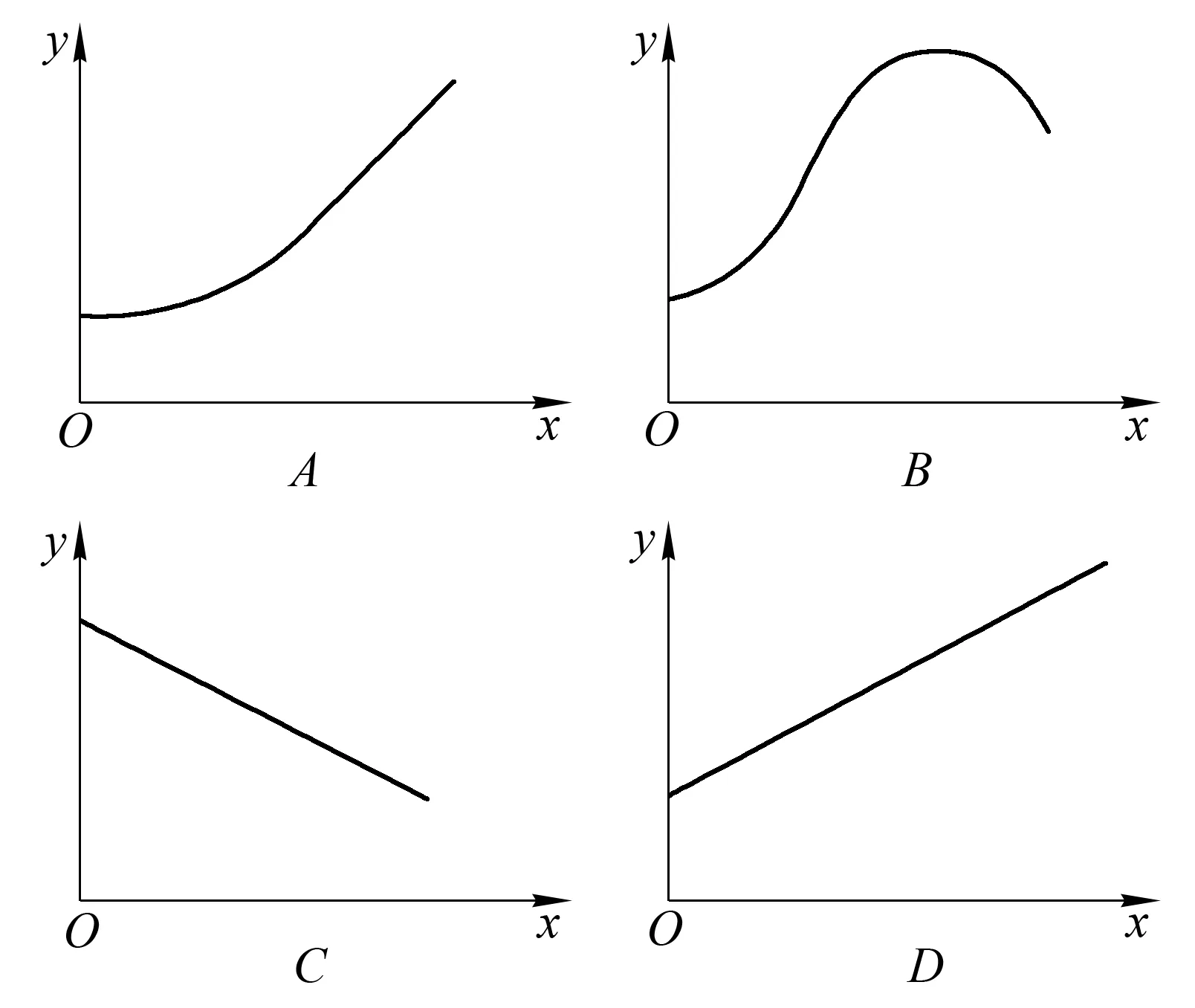
例5 (一次函数):在“植物→昆虫→鸟”营养结构中,若能量传递效率为10%,以鸟类同化的总能量中从昆虫获得的总能量为x轴,植物供能总量为y轴,绘制的相关曲线是( )。
解析:设鸟类同化的总能量为k,则鸟类通过“植物→昆虫→鸟”获得总能量x需消耗植物的量为x÷10%÷10%=100x,通过“植物→鸟”获得总能量(k-x)需消耗植物的量为(k-x)÷10%=10(k-x),故y=100x+10(k-x),化简得y=90x+10k(x>0,k>0)。由函数知识可知,它是y关于x的一次函数,其图象的特点是:①是一条直线;②在y轴上的截距为10k(k>0);③y随x的增大而增大(因斜率为90>0)。符合这些特点的曲线只有D,参考答案为D。
针对性训练4:在“草→昆虫→鸟”营养结构中,假设动物性食物所占比例为m,若以鸟体重增加的重量为x轴,至少消耗草的量为y轴,绘制的相关曲线是( )。
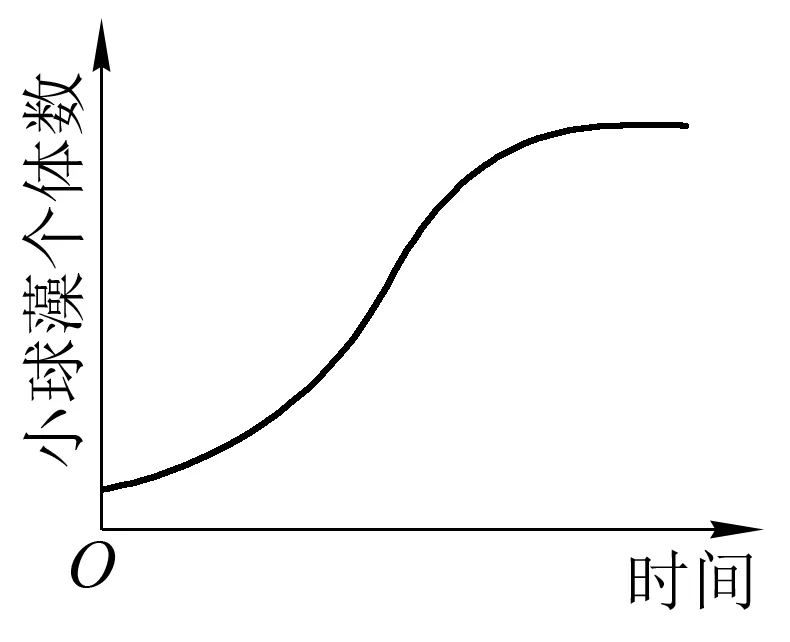
解析:当能量传递效率为20%时,消耗草的量最少。鸟通过“草→虫→鸟”增重mx时至少消耗草的量为mx÷20%÷20%=25mx,通过“草→鸟” 增重(1-m)x时至少消耗草的量为(1-m)x÷20%=5(1-m)x,故y=25mx+5(1-m)x,化简得y=(20m+5)x(x>0,0 例函数,其图象的特点是:①是一条直线;②经过原点;③y随x的增大而增大(因斜率20m+5>0)。符合这3个特点的曲线只有C,参考答案为C。 例6 (二次函数):在一个玻璃容器内,装入一定量的符合小球藻生活的营养液,接种少量的小球藻,每隔一段时间测定小球藻的个体数量,绘制成的曲线如图所示。图A、B、C、D中能正确表示小球藻种群增长速率随时间变化趋势的曲线是( )。 解析:由上图可知,小球藻种群数量呈“S”型增长。“S”型增长曲线是根据方程Nt= K/(1+ea-rt)构建的数学模型(t为时间,Nt为种群大小,K是环境容纳量,e为常数,a表示曲线对原点的相对位置,r是物种的潜在增殖能力,特定种群的r和K都为定值)。将该方程求导得dN/dt=rN(1-N/K)[1](逻辑斯谛方程,dN/dt为种群增长速率,N为种群数量,其余各参数的含义同上),将其变形得dN/dt=-r/K[(N-K/2)2- K2/4],由函数知识可知,此方程是dN/dt(因变量)关于N(自变量)的二次函数,坐标曲线为抛物线,其特征如下:①开口方向向下(因二次项系数为-r/K<0); ②对称轴为N=K/2(由上述方程可知); ③存在最大值rK/4(当N=K/2时,-r/ K[(N-K/2)2- K2/4]=rK/4); ④与横坐标的交点为N=0和N=K[当N=0或K时,rN(K-N)/K =0]。 由所述4个特征可知,参考答案为D。 例7 (非初等函数):科学家在研究基因的图距时,若某测交观察到两个基因座之间重组值为27.5%,则实际图距应为多少? 解析:根据泊松分布的概率密度函数f(x)=mxe-m/x!(其中x=0,1,2,…,m=分布的平均数)可知,某两个基因间不发生交换(零次交换)的概率f(0)=m0e-m/0!=e-m。其次,还要考虑至少发生一次交换的减数分裂的比例为1与0次交换类型比例的差。因为在许多细胞中,同一染色体上某两个基因之间发生交换的平均数必然很小,所以交换数的分布可以用泊松分布的各项表示,故作图函数可表示为RF=1/2(1-e-m)(RF为重组率)。将题中数据代入作图函数式可得0.275=1/2(1-e-m),化简得到e-m=0.45,解得m=0.8。说明在这两个基因座之间每个减数分裂中平均有0.8次交换。因为每次交换只包括4条染色单体中的两条非姐妹染色单体,故由m再转换成真实图距时应乘以1/2,即真实的图距为0.8×1/2=40 cM(cM为图距单位“厘摩”,1 cM=1%重组值去掉%的数值)。 例8 已知氨基酸的平均相对分子质量为128,测得某蛋白质的相对分子质量为5646,则组成该蛋白质的氨基酸数和肽链数分别为( )。 A.51、1 B.51、2 C.52、1 D.52、2 解析:设组成该蛋白质的氨基酸数为n,肽链数为m,根据氨基酸的质量之和=蛋白质的质量+脱去水的质量及脱去的水分子数=氨基酸数-肽链数可得,128n=5646+18(n-m),化简得18m+110n=5646,若m=1,则n=2814/55≈51.16,舍弃(因n为正整数);若m=2,则n=51,故答案为B。 例9 有一多肽链,分子式为C55H70O19N10,其彻底水解后,只得到下列4种氨基酸(R基均不含N):谷氨酸(C5H9O4N),苯丙氨酸(C9H11O2N),甘氨酸(C2H5O2N),丙氨酸(C3H7O2N)。则该多肽链彻底水解可产生多少个甘氨酸?( ) A. 1 B. 2 C. 3 D. 4 解析:设此多肽链彻底水解可产生谷氨酸a个、苯丙氨酸b个、甘氨酸c个、丙氨酸d个,则根据C、H、O、N原子守恒可分别得①、②、③、④式: 解得c=1,参考答案为A。 思维警示:用原子守恒法解题时,脱水缩合所脱去的水中H和O的个数很容易被忽略。即H、O守恒的方程式很容易出错。 针对性训练5:一条多肽链的分子式为C22H34O13N6,其彻底水解后,只得到下列3种氨基酸:谷氨酸(C5H9O4N),甘氨酸(C2H5O2N),丙氨酸(C3H7O2N)。那么该多肽链彻底水解之后可产生多少个丙氨酸?( ) A. 1 B. 2 C. 3 D. 4 参考答案:A。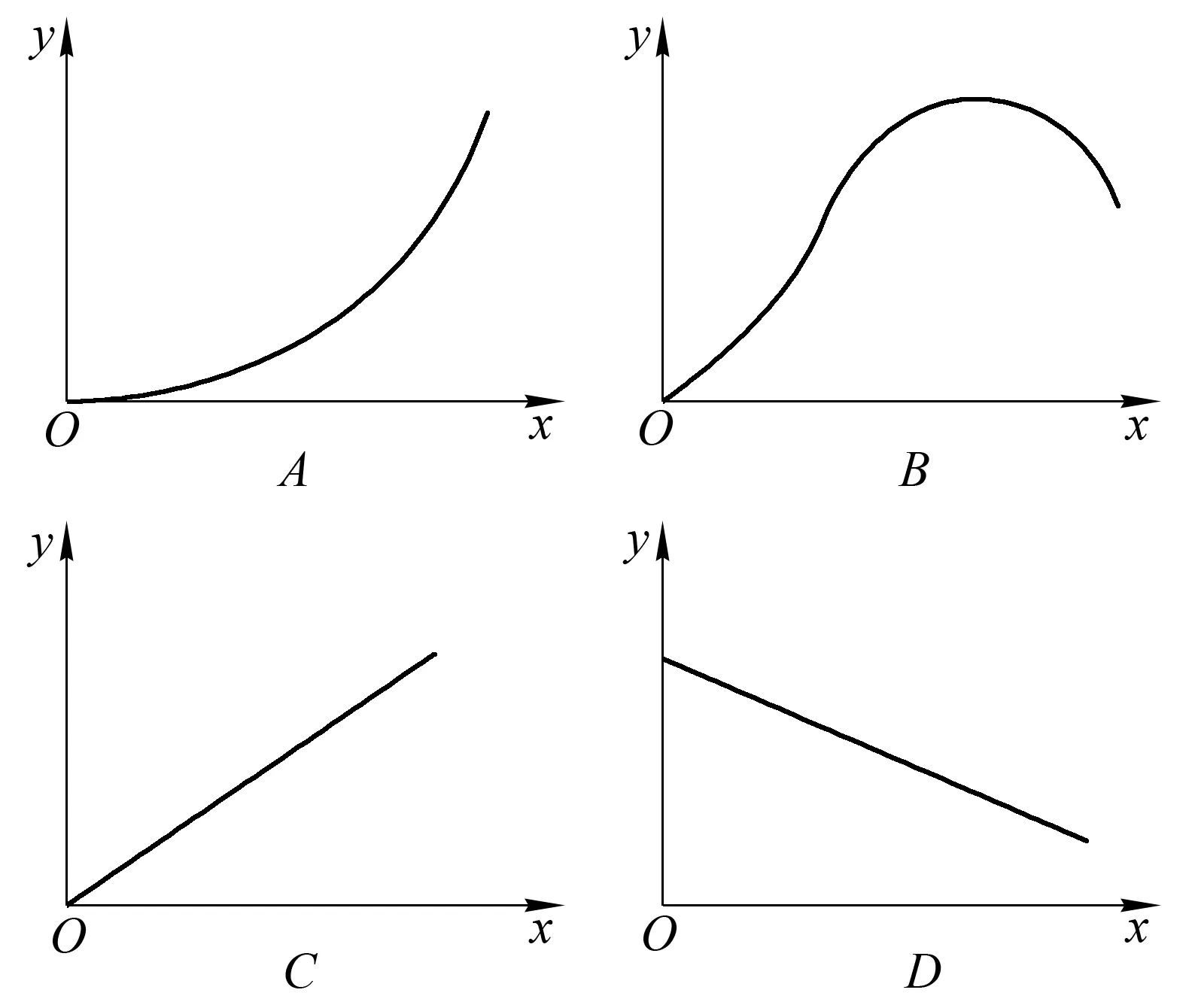

3 方程在生物学解题中的应用

