“圆”来如此简单——2015年江苏无锡中考卷第26题思路解析

邵艳



“圆”来如此简单
——2015年江苏无锡中考卷第26题思路解析

邵艳

研习2015年全国各地中考数学卷，常常为有些试题的精巧构思、苦心经营而感动.比如2015年江苏无锡卷第26题没有图形，但是求解时却对几何图形中的线段、线段中点、角平分线、平行四边形（包括菱形）、圆、直角三角形、轴对称等知识全面覆盖，是一道不可多得的好题，下面为同学们讲解该题，希望同学们有所收获.

（2015·无锡，10分）已知：平面直角坐标系中，四边形OABC的顶点分别为O（0，0）、A（5，0）、B（m，2）、C（m-5，2）.

（1）是否存在这样的m，使得在边BC上总存在点P，使∠OPA=90°？若存在，求出m的取值范围；若不存在，请说明理由.

（2）当∠AOC与∠OAB的平分线的交点Q在边BC上时，求m的值.

【思路讲解】

（1）由B、C坐标特征知道B、C两点均在直线y=2上；问题又明确指出∠OPA= 90°，则可以确认点P应该在以OA为直径的圆上.如图1，以OA为直径的圆（圆心为点M）交直线y=2于点P、P′（想一想，为什么会有两个交点？因为⊙M的半径为2.5，而直线y=2到x轴的距离为2），选取其中一个交点P研究，连接PM，作PH⊥OM于H点，在Rt△PHM中，由勾股定理可得HM=1.5，所以P（1，2），点P、P′关于直线x=2.5对称，根据对称性得P′（4，2）.

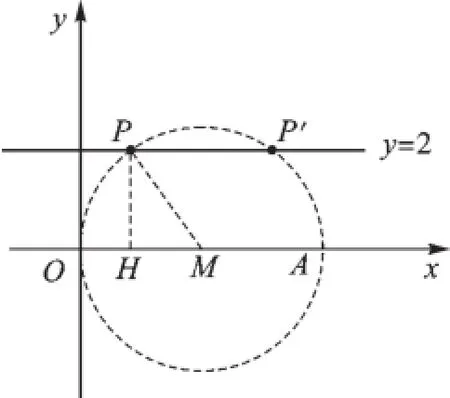
图1

接着来分析边BC的运动范围，如图2，设线段BC在直线y=2上从左侧平移而来，当端点B接触到点P时，此时点P有可能出现在边BC上，此时点B对应的横坐标m=1；

随着BC不断右移，当点C到达P′时，点P′还可能出现在边BC上，此时点C对应的横坐标m-5=4，即m=9.

离开P′时，点P、P′就都不可能出现在边BC上了.就是说当1≤m≤9时，边BC上总存在点P，使∠OPA=90°.

（2）首先解读强化条件“当∠AOC与∠OAB的平分线的交点Q在边BC上”，这说明OQ⊥AQ（理由是两直线平行，同旁内角的平分线互相垂直）.也就是说上一问中的点P、P′就可能是第（2）问中的Q点.于是构造图3分析：

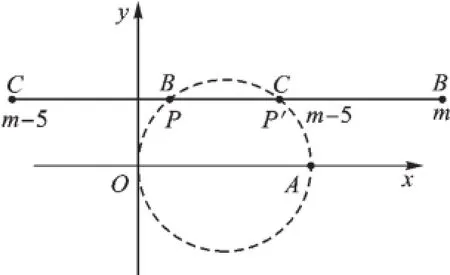
图图22

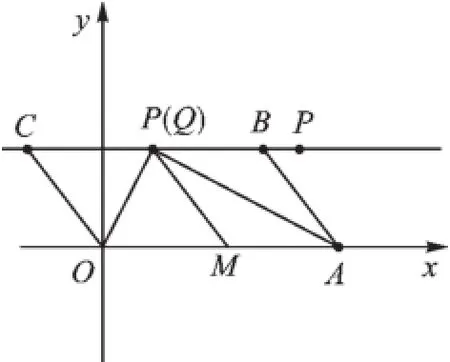
图3

当点Q落在点P（1，2）上时，此时容易得出Q为BC中点，于是点B坐标为（3.5，2），即m=3.5；

如图4，当点Q′落在点P′（4，2）上时，同样可求出点B坐标为（6.5，2），即m=6.5.

综上，m=3.5或6.5.

图4

【点评】一般情况下，存在性问题如果涉及90°的角时，常常要和直角三角形的外接圆联系到一起.这是由于在圆的学习中，有多个概念或定理涉及90°.比如：圆周角定理推论中直径所对的圆周角为直角；在圆中，90°的圆周角所对的弦是直径；直角三角形的外接圆是以斜边为直径的圆等等.（作者单位：江苏省南通市通州区西亭初中）