最小值问题的解题思考

陈云龙



最小值问题的解题思考

陈云龙

我们会经常遇见一些求最小值的考题，如求线段长度之和的最小值、三角形周长的最小值或利用最小值求点的坐标问题.解决这类问题主要是利用几何结论，如两点之间线段最短、三角形任意两边之和大于第三边、任意两边之差小于第三边、垂线段最短等.下面和同学们一起分享2015年中考数学试题中部分求最小值问题的解决方法.

例1（2015·武汉）如图1，∠AOB=30°，点M、N分别在边OA、OB上，且OM=1，ON=3，点P、Q分别在边OB、OA上，则MP+PQ+QN的最小值是_______.

图1

【分析】此题是通过作图找出M，N关于直线OB，OA的对称点，利用“两点之间，线的图像上，若△PAB为直角三角形，则满段最短”的线段公理解决问题，具有代表性.

图2

解：作点M关于OB的对称点M′，作点N关于OA的对称点N′，连接M′N′，即为MP+ PQ+QN的最小值.根据轴对称的定义可知：

∠N′OQ=∠M′OB=30°，∠ONN′=60°，

∴△ONN′为等边三角形，

△OMM′为等边三角形，

∴OM′=OM=1，N′O=NO=3，

∠N′OM′=30°+60°=90°，

∵在Rt△M′ON′中，M′O=1，N′O=3，

M′N′2=M′O2+N′O2，

【点评】本题关键是利用公理“两点之间线段最短”来求解，分别作出点M，N关于直线OB，OA的对称点M′，N′.因此必须掌握轴对称有关概念、线段公理、等边三角形相关性质、勾股定理等知识点.同学们必须具备解题思路清晰、勇于实践、敢于探索的数学思维品质.

例2（2015·南宁）如图3，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，点N是弧MB的中点，点P是直径AB上的一动点.若 MN=1，则△PMN周长的最小值为（）. A.4B.5C.6D.7

图3

【分析】作点N关于AB的对称点N′，连接MN′、NN′、ON′、ON，由两点之间线段最短可知MN′与AB的交点P′即为△PMN周长值最小时的所求点.根据点N是弧MB的中点可知∠A=∠NOB=∠MON=20°，故可得出∠MON′=60°，故△MON′为等边三角形，由此可得出结论.

图4

解：作点N关于AB的对称点N′，

连接MN′，NN′，ON′，ON.

∵N、N′关于AB对称，

∴MN′与AB的交点P′即为△PMN周长最小时的所求点，

∵N是弧MB的中点，

∴∠A=∠NOB=∠MON=20°，

∴∠MON′=60°，

∴△MON′为等边三角形，

∴MN′=OM=4，

∴△PMN周长的最小值为4+1=5.

故选：B.

【点评】本题要我们求三角形周长的最小值，而M，N为定点，因此MN=1为定值，所以要求△PMN周长的最小值就是要求出PM+PN的最小值.我们不难想到用线段公理来解决问题.解题的关键是作出点N关于直径AB的对称点N′，连接MN′交AB于点P′，利用轴对称的性质，此时P′M+P′N最小.本题把求三角形周长最小值问题转化为求线段和最小值问题，解答此题思路要清晰，涉及知识点较多，综合性较强.

（1）求k的值；

（2）求点C的坐标；

（3）在y轴上确定一点M，使点M到C、D两点距离之和d=MC+MD最小，求点M的坐标.

图5

【分析】（1）根据点A坐标，以及AB=3BD求出点D坐标，代入反比例函数解析式求出k的值；

（2）直线y=3x与反比例函数解析式联立方程组即可求出点C坐标；

解：（1）∵A（1，3），∴AB=3，OB=1，

∵AB=3BD，∴BD=1，∴D（1，1），

将点D坐标代入反比例函数解析式得：k=1.

（2）由（1）知，k=1，

（3）如图6，作点C关于y轴的对称点C′，连接C′D交y轴于M，则d=MC+MD最小，

图6

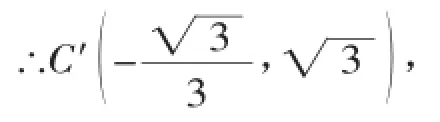
设直线C′D的解析式为：y=mx+n，

【点评】此题考查了反比例函数与一次函数的交点问题，涉及的知识点有：坐标与图形性质，待定系数法确定函数表达式，用解方程组的思想方法解决问题，直线与反比例函数图像的交点求法等.熟练掌握待定系数法，作已知点关于y轴对称点并利用线段公理求最小值问题是解决本题的关键.此题可进行变式训练，如在x轴上确定一点N，使△NCD周长最小等.

同学们在学习数学时，要开动脑筋、潜心钻研、善于积累，不断提高综合运用知识解决问题的能力，为数学学习的可持续发展奠定坚实的基础.

（作者单位：江苏省盐城市明达中学）