巧用面积法解决问题
2016-08-20刘国成
刘国成
巧用面积法解决问题
刘国成
面积法解决几何问题是一种常用的重要方法,巧用面积法解题有时显得特别简捷,有出奇制胜、事半功倍之效.现就几种类型举例说明,供同学们参考.
一、巧用面积法求线段长
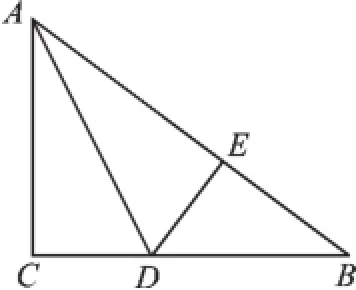
图1
例1 如图1,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为().
A.4B.3C.2D.1
【分析】由折叠的性质和勾股定理列式求出AB,从而求出BE,设CD=DE=x,表示出BD,然后在Rt△DEB中,利用勾股定理列式计算即可得解.但我们发现用面积法来求CD较为简便.
解:∵直角边AC沿直线AD折叠,与AE重合,
∴CD=DE.
由S△ABC=S△ACD+S△ABD,
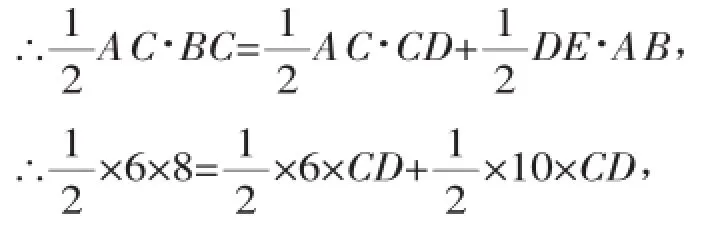
解得CD=3.故选B.
【点评】本题考查了翻折变换的性质,由角平分线性质得CD=DE,再利用勾股定理的应用,求出斜边AB,然后由AD把Rt△ABC分成△ACD和△ADB,利用面积法建立方程求出CD=3.
二、巧用面积法证明线段相等
例2 如图2,已知△ABC≌△A′B′C′,AD、A′D′分别是BC、B′C′边上的高,AD和A′D′相等吗?请说明理由.

图2
【分析】同学们常常用证全等的方法来说明两条线段相等.我们也可根据三角形的高,联想到用三角形的面积来说明线段相等.
解:AD=A′D′.理由如下:
∵△ABC≌△A′B′C′,
∴S△ABC=S△A′B′C′,CB=C′B′,
∵AD、A′D′分别是BC、B′C′边上的高,
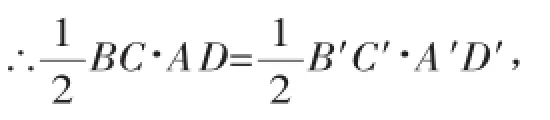
∴AD=A′D′.
【点评】这种方法简洁明了.如果出现了高,要联想三角形的面积,有时会出现事半功倍的效果.
三、巧用面积法证明线段比相等

图3
例3如图3,AD是△ABC的角平分线.求证:AB∶AC=BD∶DC.
【分析】本题我们可采用过C作AD的平行线,用平行线分线段成比例来证明,但由于AD是△ABC的角平分线,我们想到AD上的点到角两边距离相等,再想到三角形的面积,思路更为简洁.
证明:过D点作DE⊥AB,DF⊥AC,垂足分别为E、F.
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,则有S△ABD∶S△ACD=AB∶AC.
过A点作AH⊥BC,垂足为H,
则有S△ABD∶S△ACD=BD∶DC.
∴AB∶AC=BD∶DC.
【点评】本题要证明线段的比相等,正常的思路是用相似来解决问题,但我们用面积法来证明则更加简单明了.
四、巧用面积法证明线段和差
例4(2014·盐城,有删减)【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图4,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.

图4
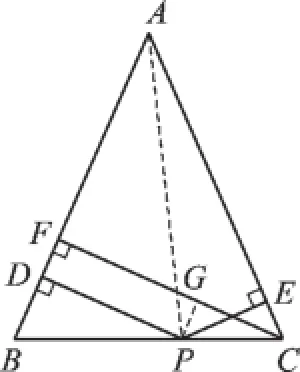
图5
小军的证明思路是:如图5,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图5,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE= CG,则PD+PE=CF.
请完成小军和小俊的证明过程.
【变式探究】如图6,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF.
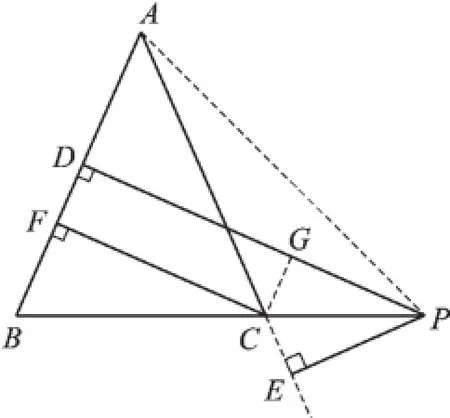
图6
【分析】【问题情境】如图5,按照小军、小俊的证明思路即可解决问题.
【变式探究】如图6,借鉴小军、小俊的证明思路即可解决问题.但细细阅读可知小军的解答思路简洁,用面积法出奇制胜,节约时间.
证明:【问题情境】(小军)连接AP,如图5,
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP+S△ACP,
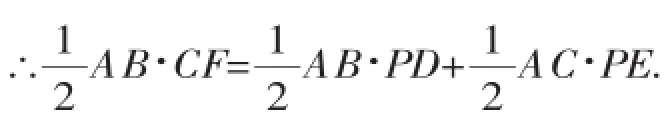
∵AB=AC,∴CF=PD+PE.
(小俊)过点P作PG⊥CF,垂足为G,如图5.
先证明:△PGC≌△CEP(AAS),
∴CG=PE,
∴CF=CG+FG=PE+PD.
【变式探究】
(小军)连接AP,如图6.
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP-S△ACP,
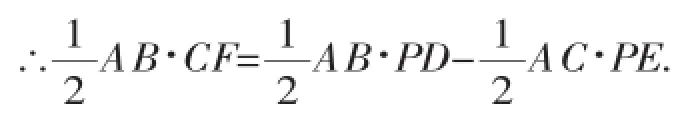
∵AB=AC,∴CF=PD-PE.
(小俊)过点C作CG⊥DP,垂足为G,如图6.
易证:△CGP≌△CEP(AAS),
∴PG=PE,
∴CF=DG=DP-PG=DP-PE.
【点评】本题考查了矩形的性质与判定、等腰三角形的性质与判定、全等三角形的性质与判定.考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力.在解题中,如遇有多条垂线就可联想到用三角形的面积,巧妙地将三角形的面积分解成几个三角形面积的和或差解题较为简便.
面积法不仅可以巧妙地求出线段的长、证明线段相等、证明线段比相等、求线段和差,而且可以从一点到一个角的两边的距离相等,证明这个点在角平分线上,希望同学们加以体会,细心研究,灵活应用面积法解题.
(作者单位:江苏省盐城市明达中学)
