整式乘法与因式分解易错题问诊

鲍文碐



整式乘法与因式分解易错题问诊

鲍文碐

整式乘法运算和因式分解是基本而重要的代数知识，是进一步学习分式和根式运算、函数等知识的基础，在后续的学习中具有重要意义.同时，这些知识还是学习物理、化学等学科不可缺少的数学基础知识.但同学们在进行整式乘法与因式分解时，常常会出现这样或那样的错误.为了帮助同学们尽可能地避免错误，及时走出误区，现就常见错题展示问诊.

例1计算：（2x3y）2（-3x2y3z）.

【错解一】原式=2x6y2（-3x2y3z）=-6x8y5z.

【错解二】原式=4x6y2（-3x2y3z）=-12x8y5.

【错因问诊】错解一的病因：积的乘方法则未理解，应将每个因式分别乘方，尤其是数字因数.

错解二的病因：计算结果丢掉了字母z.

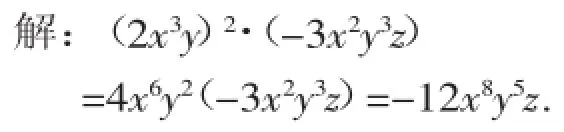
【点评】单项式乘单项式，若运算中含有乘方运算，应先算乘方，再进行单项式的乘法运算.

例2计算：-3x（x2-xy+1）.

【错解一】原式=-3x3-3x2y+3x.

【错解二】原式=-3x3+3x2y.

【错因问诊】错解一的病因：忽略了单项式“-3x”的符号.

错解二的病因：单项式乘多项式的法则没有掌握，要用-3x乘多项式的每一项，-3x与常数项1漏乘了.

解：-3x（x2-xy+1）=-3x3+3x2y-3x.

【点评】单项式与多项式相乘，一要注意符号的确定，二要注意用单项式分别乘多项式的每一项，尤其不要漏乘常数项.

例3计算：（3a-2b）（5a+3b）.

【错解】原式=15a2+6b2.

【错因问诊】多项式的乘法法则未掌握，第一个多项式中的每一项要分别乘第二个多项式的每一项.本题两项的多项式乘两项的多项式时，应得四项，然后再进行合并同类项.

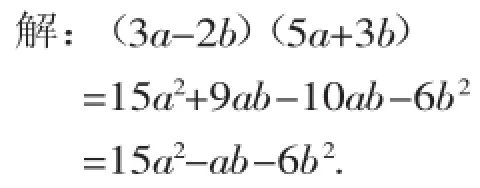
【点评】多项式乘多项式要注意以下几点：

1.不重不漏.

2.注意符号.

3.结果中有同类项，要注意合并同类项.

例4运用公式计算（-2x-3y）（3y-2x）.

【错解】原式=（3y）2-（2x）2=9y2-4x2.

【错因问诊】未理解公式（a+b）（a-b）= a2-b2中a和b的本质.这里的-2x相当于公式中的a，而3y则相当于公式中的b.错解把a、b的位置颠倒了.

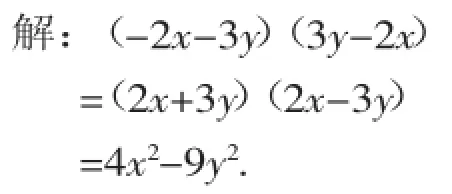
例5计算：（-2x-3y）2.

【错解一】原式=（2x+3y）2=4x2+9y2.

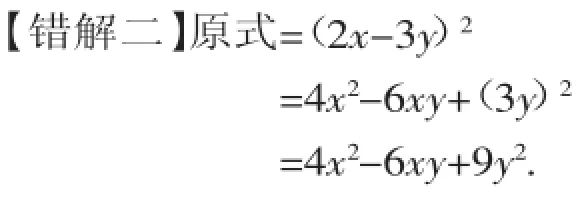
【错因问诊】错解一的病因：完全平方公式混淆未理解，要注意（a+b）2≠a2+b2（a≠0，b≠0）；

错解二的病因：1.误认为-2x-3y是两数之差，选择了差的平方公式，实际上-2x -3y与2x+3y互为相反数，应选用和的平方公式.2.“2倍乘积项”未理解，这些都是同学们常会出现的错误.

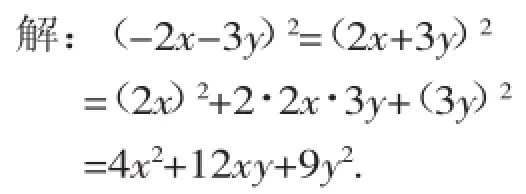
例6计算：（x-2y+3z）（x+2y-3z）.

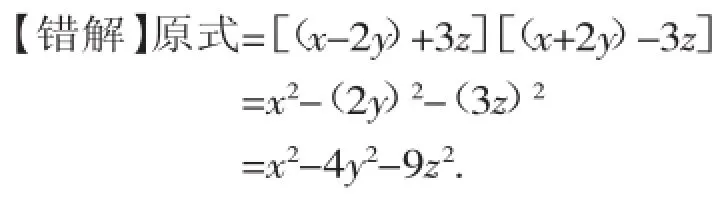
【错因问诊】误认为可以利用公式（a+ b）（a-b）=a2-b2，而实际上2x+y与2x-y并不满足公式中的a.

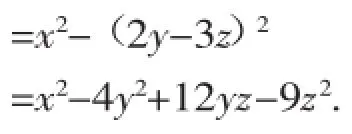
【点评】应用平方差和完全平方公式，首先必须牢记完全平方公式、平方差公式，其次分析多项式的特点是否符合公式的条件，最后运用时要分清公式中的两数是指哪两个，尤其是经过适当变形后才能应用公式的更应注意，这样才能正确灵活地解题.

例7因式分解：3x2-6xy+x.

【错解一】原式=x（3x-6y）+x.

【错解二】原式=x（3x-6y）.

【错因问诊】错解一的病因：因式分解的定义没有掌握，因式分解要求的最终结果是写成整式的乘积形式，上题中的结果是和的形式，只顾前不顾后.

错解二的病因：“1”作为单独一项时，在因式分解中不可漏掉.

解：3x2-6xy+x=x（3x-6y+1）. 例8因式分解：4x4-8x2+4.

【错因问诊】错解一的病因：因式分解的基本步骤未掌握.应首先考虑提公因式法，然后考虑用公式法.正是因为未将公因式提出，而导致分解不彻底.

错解二的病因：分解不彻底.最后要再检查所得结果是否分解彻底，否则就前功尽弃..

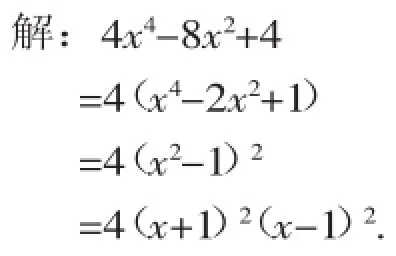
（作者单位：江苏省太仓市实验中学）