自旋-1/2算符对易关系和中心库仑场定态粒子概率密度的讨论

林　炯，陈　军，高伟康

（华南师范大学 物理与电信工程学院，广东　广州　510006）

自旋-1/2算符对易关系和中心库仑场定态粒子概率密度的讨论

林炯，陈军，高伟康

（华南师范大学 物理与电信工程学院，广东广州510006）

从Stern-Gerlach实验及其两个拓广实验出发，结合量子力学假设，给出了自旋-1/2算符对易关系的一种导出方法。每个方向的自旋本征态均构成Hilbert空间完备基，可用完全性关系将x、y、z三个方向自旋-1/2算符用相应本征态表示出来。接着通过两个拓广实验可初步确定x、y方向自旋本征态与z方向自旋本征态的关系。进一步各算符可表示成只含有z方向自旋本征态。通过Hilbert空间态矢间的运算法则，最终可得到三个方向间自旋-1/2算符对易关系。另外一个问题，对于中心库仑场含时定态波函数对应的概率密度出现空间不对称情况，通过对比库仑场经典解，发现经典系统粒子初速度已经破坏了系统空间对称性。对应到量子系统，发现初态概率密度空间不对称是其原因。

自旋-1/2；对易关系；中心库仑场；概率密度；空间不对称

0　引言

讨论自旋-1/2时，一般将对易关系和实验结果作为出发点［4］。实验与对易关系的联系很少被讨论。从实验出发，结合量子力学假设，可给出自旋-1/2算符对易关系。另一方面，对于中心库仑场定态波函数对应概率密度出现空间不对称，给出一种解释。

1　自旋-1　/2　算符对易关系一种导出方法

1.1量子力学测量理论

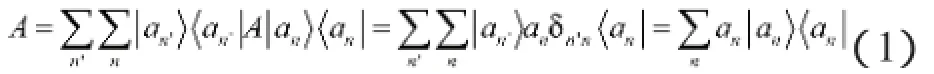
1.2自旋-1/2算符对易关系的导出

1.2.1Stern-Gerlach实验［4］

从K极射出的s态氢原子进入不均匀磁场，在照片上出现两条强度相等的分立线。s态氢原子角量子数为0不可能引起线分立。为解释此类现象，引入自旋角动量。

1.2.2对易关系的导出

δ1是任意相因子。对于，考虑到与应正交，则：

δ2为任意相因子。

由（1）式，x、y方向自旋-1/2算符：

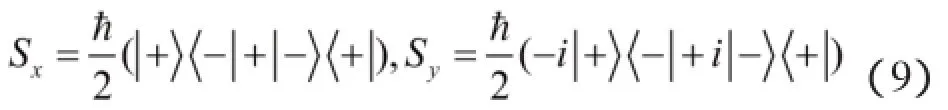
（4）由（2）（9）式，可得自旋-1/2算符对易关系：

2　中心库仑场定态波函数解对应概率密度的空间不对称问题

2.1中心库仑场含时定态波函数解

单粒子处于中心库仑场（场源电荷量）相应定态Schrödinger方程为：

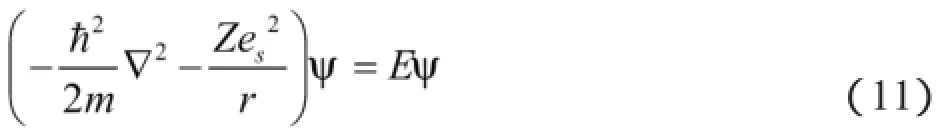
则含时定态波函数为：

2.2定态概率密度角分布现象

t时刻定态粒子概率密度即时刻t测量到粒子出现在某空间点单位体积内的概率为。可以证明，当粒子角量子数l≥1，，即定态粒子概率密度

出现角分布现象。

2.3空间对称性

若对系统进行X操作，系统状态不变，则系统在X操作下具有对称性。中心库仑场对绕过原点任意轴旋转操作保持不变，则具有球对称性，数学上由SO3群描述。

2.4概率密度角分布解释

若系统是空间对称的，粒子出现的可能概率应空间对称，不出现角分布。因此系统必存在不对称条件。

考虑中心库仑场的经典力学解。由比耐轨道微分方程［5］：

其中e为常数。由（12）式可得轨道离心率为：

自旋角动量，结果有：e＜0，轨道为椭圆；当E=0时，e=0，轨道为抛物线。

经典力学解的轨道对称性没有达到SO3。出现对称性最高的为圆周运动，轴对称可由SO2群描述。寻找经典力学系统的不对称性是比较直观的。一旦体系粒子初速度被事先确定下来，空间对称性便被破坏了。

3　结束语

结合Stern-Gerlach实验及其拓广实验和量子力学假设导出自旋-1/2对易关系。但过程中引入的两个相因子选取还有待进一步讨论。在讨论量子力学问题时，与经典力学相比照是一种常用方法。对于中心库仑场含时定态波函数对应概率密度出现空间不对称，通过对比经典解指出初态空间不对称是其原因。当然本问题还可以有其他分析方法。

［1］ 董向成，郭中华.电子自旋概念及其实验验证［J］.甘肃科技纵横，2008（02）：37+21.

［2］ 张亚新.关于电子自旋的实验验证和理论思考［J］.大学物理实验，1996（02）：9-10+14.

［3］ J.J Sakurai and Jim Napolitano.MODERN QUANTUM MECHANICS［M］.2nd，Beijing：BEIJING WORLD PUBLISHING CORPORATION.2011.

［4］ 周世勋.量子力学教程（第二版）［M］.北京：高等教育出版社，2009：172-174.

［5］ 周衍柏.理论力学教程（第三版）［M］.北京：高等教育出版社，2009：50-51.

［6］ 李远德.电子在库仑场中的运动［J］.重庆交通学院学报，1987（02）：135-138.

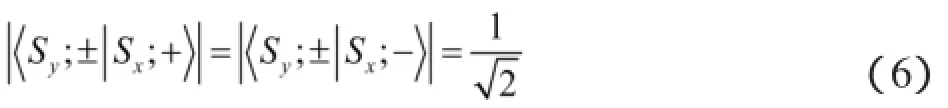
O413

A

10.3969/j.issn.1672-6375.2016.07.029

2016-4-8

林炯（1993-），男，汉族，广东汕头人，大学本科在读，主要的研究方向：物理学。