几种情况下弹性球与平板碰撞分析

◇ 江苏 甘 泉

几种情况下弹性球与平板碰撞分析

◇ 江苏 甘 泉

空心球与平板弹性运动力学的问题,一直受到国内外科学家和工程师们的重视,并基于此发表过许多相关的论著,时至今日,由于普遍受到各种客观因素的影响和限制,再加上考虑到惯性项问题,在研究的过程中,无论是对于空心球与平板之间的弹性动力还是对于球与球之间的碰撞关系,其计算难度无形之中都在增大.因此,有关这些新型材料的力学性能及其产生的相关动力学问题也在进一步研究之中,同时也给人们提出了许多极具挑战趣味的研究课题.本文就基于径向应变情形的空心球与平板弹性运行力学情景,利用碰撞知识来深度解决这一物理问题.

将一个具备高弹性的超级球扔进2块平板之间,扔掷的时候尽可能保证该超级球能够弹跳起来;在反复实验过程中,超级球运动轨迹变化多端,甚至有的时候会弹回来砸到实验人员.本文基于这个实验装置,进一步分析在此次实验过程中可能会对超级球的弹跳和运动轨迹产生影响的相关参数,探讨在径向应变情形下,球与平板之间所发生的弹性碰撞及其关系,包括理想情况下的弹性碰撞和非弹性碰撞.

1 超级球问题的延伸

关于超级球弹跳运动的问题,在这里以小球反跳实验来推导出它的表达公式,即弹跳高度公式.在问题探究之前,先介绍一下其中一个重要物理概念“恢复系数”(coefficientofrestitution).

如图1所示,其中包括一个大球和一个小球,假设图中大球的质量是m0,小球的质量为m,将小球置于大球正上方,笔者在该问题所进行的实验中,从高度为h的地方使2球一起进行自由落体运动,小球和大球均是以的速度落到地面上.在这一过程中,大球到达地面时将会与地面发生较为激烈的碰撞,在这里设大球与地面发生激烈碰撞时的恢复系数为e1,大球在到达地面后的向上反弹速度设为v1,则有v1＝e1v0.由于大球与地面发生碰撞时间极短,所以在这里暂且不考虑大球与地面碰撞的时间.那么,大球在到达地面开始向上反弹的时刻,大球上方的小球仍然是以速度v0正在向下(向地面)做自由落体运动,这时大球以速度v1与速度为v0的小球发生碰撞.再次假设大球小球没碰撞的恢复系数为e2.大球与小球在发生碰撞的过程中满足动量守恒表达公式

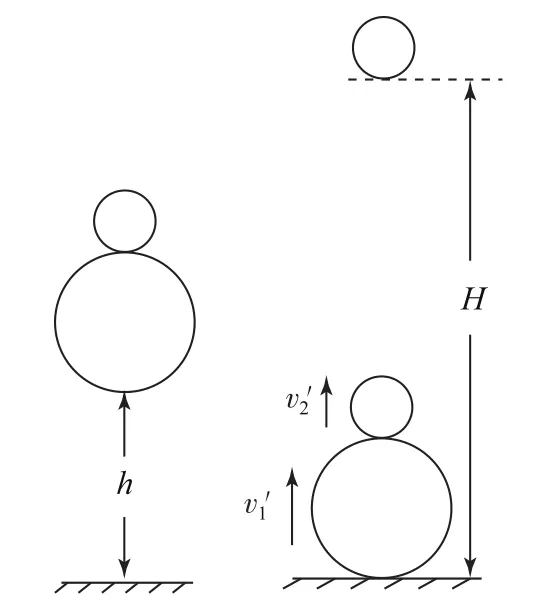
图1 超级球反跳实验

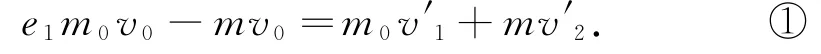
由动量守恒公式进一步得出e2的表达式

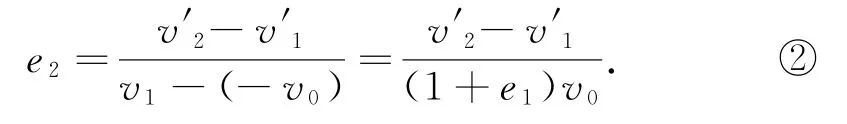
由式①、②可计算解出

因此,最后得出小球所能够上升的高度

2 空心球与墙面碰撞情况

2.1 问题的提出

物体之间的碰撞是现实生活中一种相当复杂的物理现象,其复杂性在于物体之间碰撞持续时间较短,并且两物体之间接触点间存在较大的接触力等方面.关于空心球与平板之间的弹性碰撞关系验证,无论是在弹性运动力学的研究中,还是在现实工程应用中,其所提供的参数信息一般只适用于特殊情况,即最理想化的弹性碰撞状态.

下面我们以径向应变情形的空心球与平板弹性运动问题为例进行分析.首先我们做一个简单实验.如图2所示.

图2 空心球与墙面(非)弹性碰撞

图2表示的是空心球体与两相互垂直平板之间接触的截面图,a和b分别表示的是墙体和地面,而圆形表示的是一个质量为m、半径为R的足球,它在地面b上做无滑滚动,其球心的滚动速度为v0,将足球向墙壁与地面组成的垂直角方向滚动.墙壁a为一面粗糙的墙面,其摩擦因数设定为μ,假设球与墙面之间的碰撞为完全非弹性碰撞,那么问题出现了,发生碰撞之后的足球究竟会怎样运动下去呢?是否会向上滚(弹跳起来)?如果跳起其高度会有多高?这个问题在不少物理弹性力学辅导资料中几乎给出了较为一致性的答案,即球的上升高度为.其答案似乎在告诉我们,该运动进行时,只要摩擦因数μ不等于0,无论它数值多大或多小,足球都会弹跳起来.这个问题我们可以参考超级球的处理理念,不过上述这个答案显然是不够准确的,它将摩擦因数当成对球体运动唯一起到影响效果的因素,同时也不适用于表述现实生活中的一些基本情形.

上述情形中所描述的弹性运动中存在摩擦力Ff,因为足球从开始运动算起,一直到与墙面a碰撞之前,在这一过程中,足球一直不停转动.当足球与墙面a发生碰撞后,此时摩擦力Ff的方向将会发生转变,因为此时足球的运动从水平运动转变为竖直向上运动(理想情况下是这样的),此时的球面受到墙面一个向上的力.因此,要想确保该足球能够继续向上滚动,就必须满足以下条件,即

后者表示的是足球与墙面间的平均作用力,而T则表示的是它们之间的碰撞时间,因而在0＜μ＜1的情况下,存在.在弹性运动力学的研究中,很多情况下由于缺乏相应的实践活动作为理论基础,所以经常会看到,许多物理力学问题被过多演变成为数学问题,就如同上述提到的这一问题,只要满足mg,μ不等于0,无论μ的数值多小,足球都会跳起来.但从纯物理的角度来看,如果摩擦因数μ值太小的话,质量为m的足球是不足以被弹起的,因此在探讨和研究空心球与平板弹性运动时,关于摩擦因数的大小的谈论是非常有必要的.总之,足球(碰撞弹起)上升高度是一个不合理的答案,该公式只有在一种情况下才可能适用,即墙壁a对足球的摩擦力远大于足球重力的情况下.

2.2 定性分析

如图2所示,足球在以初速度v0和初始角速度ω0与墙壁a发生碰撞,该碰撞为非弹性碰撞.足球与墙壁在碰撞过程中,由于受到墙壁a的弹力,以及自身所拥有的初始角速度等外在力的影响,导致了墙壁对足球有了一个向上的摩擦力Ff,一旦摩擦力Ff大于足球的重力时,该足球在第一时间并不会向反方向弹回去,而是在结束碰撞运动之后的瞬间,其内外力将会发生质的转变:水平方向从原来的水平速度v0减至为0,与此同时,相应产生一个竖直向上的速度vc.实验人员在将足球滚向墙体的过程中,足球始终都是在水平方向运动的,而足球的水平动能在碰撞发生之后就完全损失消耗掉了,其中的部分动能是由摩擦耗散掉的,而另一部分则迅速转化为质心向上的平动能.当足球(弹起)上升到最高点时,向上的质心平动能在此刻将会全部转变为重力势能.在这个过程中,涉及摩擦力、支持力,同时还有来自于墙壁对足球的碰撞力但由于在实验过程中,碰撞力远大于其他外力(包括摩擦力、支持力等),所以在运用动量定理的时候,我们可以忽略其他外力.最终依据动量定理,可以得出足球在水平方向上满足依据质心运动定理,可以得出足球在受到重力mg和墙壁a对它产生摩擦力时的动力学方程

3 球与竖直平行平板之间的碰撞

3.1 理想情况下弹性球与竖直平行平板间的弹性碰撞

设置实验装置,如图3所示,将一个高弹性球以抛物线的运动轨迹扔向2个平行平板组成的空间内(平板M和平板N).首先我们假设N平板不存在,如图4所示.

图3

图4

设当某人将这个高弹性小球面向平板M以初速度v0水平抛出去的时候,抛出点与地面的距离为h,同时抛出点到平板M的水平距离为s,球与平板M碰撞后反弹落地点到平板M的距离为2s.在理想情况下,由于球与平板M碰撞的时间极短,其在碰撞发生时球的动能没有发生改变,而是在反弹后会朝着相反的方向做水平下抛运动,由此可计算出球的初速度

球与平板M碰撞后,动能没有损失,此时球水平分速度反向、竖直分速度大小和方向都没有发生变化,因此,基本可以看作是该球从抛出点到落地点沿着竖直方向进行的自由落体运动,因而计算出

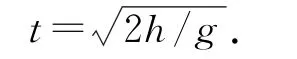
再来分析图3,当球在两平行平面内进行连续的反弹碰撞运动时,此时球的动能会随着第2次、第3次……第n次碰撞出现变化,但总量是保持不变的(理想情况下).与此同时,球在空间内的运动轨迹本身就是一个变相的平抛运动(如图5所示),当小球与地面发生碰撞的时候,同样该球也没有能量损失.

图5

在整个弹性碰撞运动的全过程中,球水平速度v0不变,已知球运动时间从而得

在不考虑空气阻力的理想情况下(空气阻力极小,所以无论考虑还是不考虑空气阻力等相关影响因素,高弹性球在正常情况下基本可以回到原先的高度位置),小球要想回到之前所处的高度,就必须补偿整个碰撞运动过程中损失的机械能.所以,本次暂且忽略掉球在与地面发生反弹碰撞之后上升回原来的高度过程中所需要克服的空气阻力,只需要考虑球回到原先高度所需要克服的重力做的功.

3.2 理想情况下弹性球与竖直平行平板间的非弹性碰撞

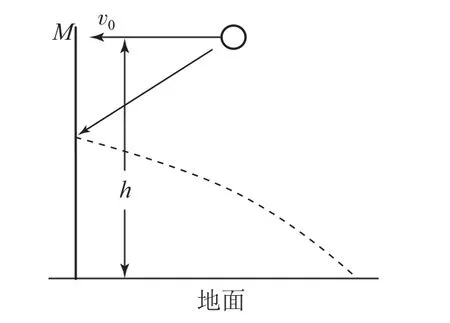
图6

关于这一情况,我们可以联想一些实例,如乒乓球运动.如图6所表示的是球与平板M的弹性碰撞运动,关于非弹性碰撞,假设图中的球是一个“乒乓球”, M是球拍.当然,在碰撞的过程中,球拍也是运动着的,如图7所示.

图7

图7表现的是球与拍面之间的碰撞模型.2个物体在同时运动的过程中,其机械能必然会出现不同程度的损失,并且2个物体在发生碰撞之后,彼此之间又迅速分离,这种碰撞运动现象就是非弹性碰撞运动.

如图8,球和平板之间的碰撞运动是非完全弹性碰撞关系,当球与平板接触时,球的机械能发生损失,而平板M实际上阻挡了球的运动轨迹.球在与平板M碰撞之后,又迅速分离,弹性球的机械能减小,显然弹性球与平板碰撞后分开的速度与碰撞之前速度成正比关系,根据前面讨论的关系模型可得出其中恢复系数e在0～1之间.

图8

4 球与水平平行板之间的碰撞

4.1 理想情况下弹性球与水平平行平板间的弹性碰撞

如图9所示,将弹性球抛向设定空间内,球在此空间内的运动轨迹如图10所示.

图9

图10

在第1次碰撞之后,因球质量不会发生变化,系统内只有重力和弹力做功,机械能守恒.可以理解为球与平板碰撞前的动能等于碰撞后的动能,所以可以认为球在离开平板N之后瞬间的速度应该和球与平板N碰撞之前速度一致.也就是说,将球抛下后,实际上球一直在进行一个上下的往复运动,能量一直恒定.

4.2 非理想情况下弹性球与水平平行平板间的非弹性碰撞

假设该弹性球是一个小型的高弹性皮球,如图11所示.

图11

那么,球在与平板N发生碰撞的那一刻,肯定会产生一定量的能量损失,在碰撞之后,球的一部分动能会转化为热力学能,也就是说,无论是垂直下抛、还是如图11所示的斜抛,球在与平板N碰撞反弹之后,一般回不到原先下落时的高度位置.也就是说,皮球在上下弹跳数次之后,能量会逐渐消退,最终变成缓慢地在平面上滚动,直至停止.

弹性球与平板碰撞现象是生活中常见的物理现象,由于碰撞时间极短,影响因素复杂(球的大小、形状、质量、空气阻力、接触面情况等),所以在具体研究过程中通常会做理想化处理,这也是物理研究的一种基本方法.另外,碰撞问题通常会涉及能量与动量关系,这也是我们解决此类问题的切入点.

(作者单位:中国人民解放军理工大学军事气象专业(理学院六营))