基于区间分隔的卡车车架轻量化设计

胡朝辉　张　健　李光耀　袁智军

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.上汽通用五菱汽车股份有限公司，柳州，545007



基于区间分隔的卡车车架轻量化设计

胡朝辉1张健1李光耀1袁智军2

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.上汽通用五菱汽车股份有限公司，柳州，545007

采用拓扑优化方法进行轻量化设计时，若模型较大，则直接拓扑计算的结果会比较混乱，针对此问题，提出一种基于区间分隔的车架轻量化设计方法。先根据使用要求把拓扑区间分隔成几个小的区域以使计算结果更加清晰；然后采用基于拓扑计算的高强度螺栓优化布置方法以bar单元模拟螺栓并计算其相对密度；最后，根据计算结果准确地确定零件中高强度螺栓的位置。在对某型卡车车架结构进行轻量化设计的过程中，始终以保证其刚度和强度等性能满足典型工况的使用要求为前提，同时根据设计目标的不同不断调整、细化设计变量与约束条件，再综合使用拓扑优化和尺寸优化法求解。结果显示，该车架优化设计后总质量减小了60.4 kg，减重率超过10%。

轻量化；概念设计；拓扑优化；螺栓优化

0　引言

节能、环保和运载能力往往被作为评价卡车产品性能优劣的宏观指标，而它们实际上都与卡车的质量密切相关，当卡车质量减轻之后这些性能都会得到显著提升，最终将提高产品在市场上的生命力。车架是卡车整体结构中连接和承载车身各零部件的关键总成，同时在整车质量中所占的比重很大，所以如果能在保证卡车使用性能不受影响的前提下对车架实施轻量化设计，就能在降低油耗和生产成本的同时提高卡车的有效运载能力。

车架结构的轻量化设计是多学科优化问题，设计中会涉及一系列如零件几何特征、材料性能等参数和零件的变形量、应力等约束条件[1-3]，而且最终必须统一到整车系统中。对于这样的复杂系统,很多工程师和学者已从实践出发提出了针对汽车刚度、强度、碰撞甚至疲劳等方面的优化措施[4-6]，并且最终取得了成功，为人们提供了有效的轻量化设计手段，但在正向开发设计时却没有完整的步骤可循，这在一定程度上影响了轻量化设计方法的应用。

在对某卡车车架进行轻量化设计时采用了基于区间分隔的拓扑优化设计和基于拓扑计算的高强度螺栓优化布置。前者要求在概念设计时根据车架的使用要求先把拓扑空间分成若干小区域，然后再加载计算以缩短解读模型的时间；后者则使用拓扑算法确定结构中高强度螺栓的位置，使高强度螺栓位置的确定简单、准确。模型设计结束后又以实车试验结合典型工况下模拟分析的方式对轻量化结果进行验证，最终得到了切实可行的优化方案。

1　车架的优化设计流程

根据分析目标的不同，车架的轻量化设计可分为结构设计和尺寸设计两个阶段，实质就是把设计过程的多学科问题逐步简化为单学科问题以利用现有的方法解决当前设计问题[7]。其设计流程如图1所示。

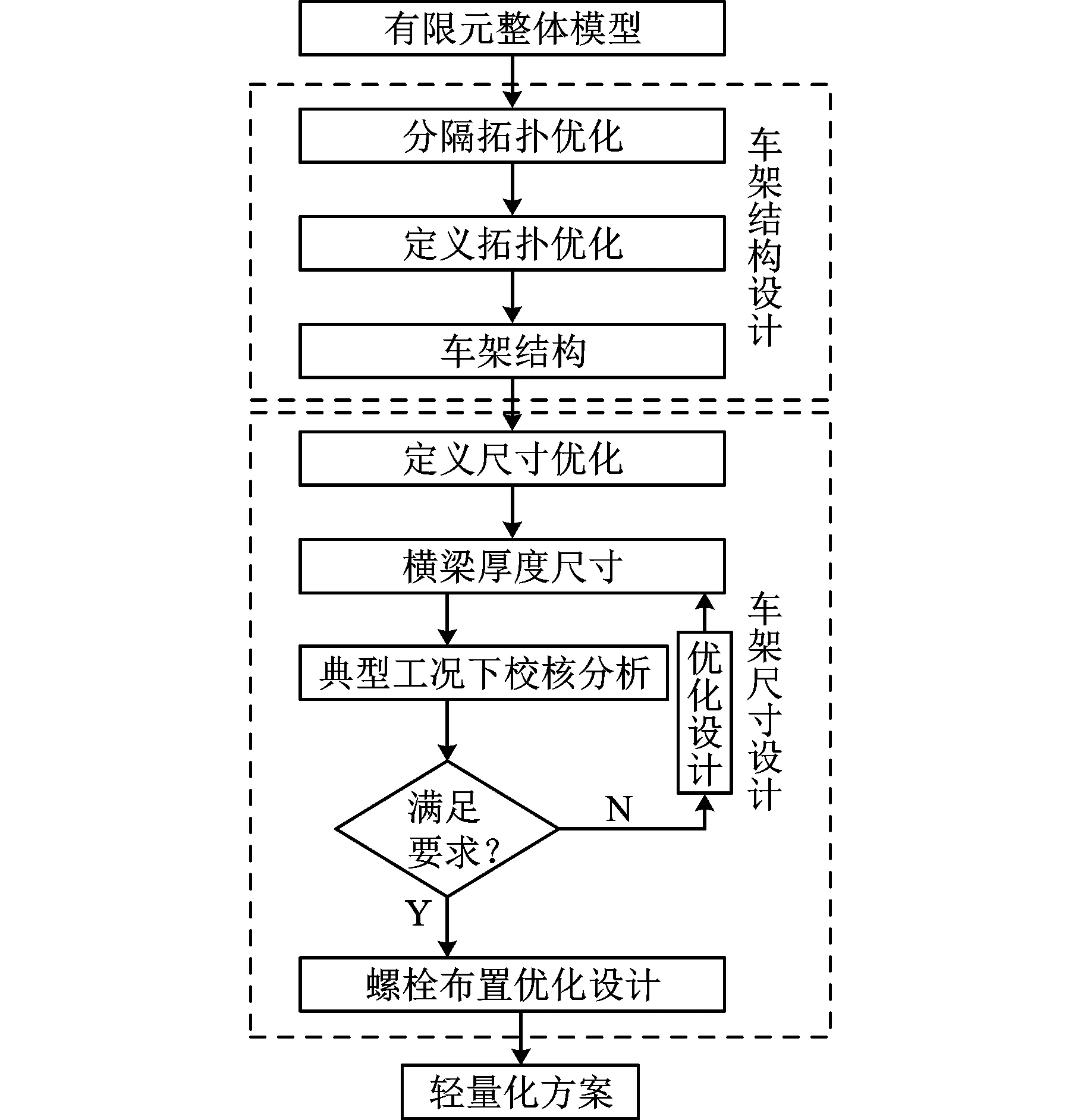
图1　车架轻量化流程

2　车架的优化设计方法

2.1基于区间分隔的拓扑优化

以连续体结构柔度最小为目标，同时以全局体积为约束条件时，变密度法的数学模型为

Findρ=(ρ1,ρ2,…,ρn)T∈R

minC=FTU

s.t.V*≤fV

F=KU

0<ρmin≤ρi≤1i=1,2,…，n

式中，ρi为材料单元的相对密度；C为结构整体的柔度值；K为整体结构刚度矩阵；U为整体位移列向量；F为外载荷向量；V为整体结构体积；V*为优化后的结构体积 ；f为保留的体积分数。

一般情况下，如果按上式定义直接对模型进行拓扑求解，其计算结果会形成混乱的整体。图2为一前端受扭转力矩、末端约束的平板结构模型，以设计区的材料密度为设计变量的拓扑结果如图3所示。

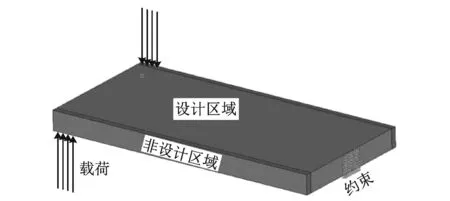
图2　直接拓扑计算模型

图3　直接拓扑计算结果

卡车车架是连接其他总成的主体，所以车架的横梁必须对应其他零件的安装位置分布在纵梁之间，但图3的计算结果显然不满足这个要求，这将给之后的模型诠释工作带来巨大的困难。采用SIMP材料插值模型计算时为使每个单元的密度值尽量趋向0或1，有：

令

φ(ρi)=0ρi∈M,N,Q

其中，p为惩罚因子，p=3;M、N、Q为特定集合。

在保证其他条件不变的情况下去除板中M、N、Q三个位置的材料(图4)，重新计算后其拓扑结果如图5所示。

M、N、Q——拓扑区域中被去除材料的空间图4　分隔区间后的拓扑计算模型

图5　分隔区间后的拓扑计算结果

可见尽管加载条件一致，拓扑结果图3与图5却有明显的区别，这是由于当设计空间被分为几个小区域之后载荷在材料中的传递路径发生了改变。由Kuhn-Tucker优化准则有

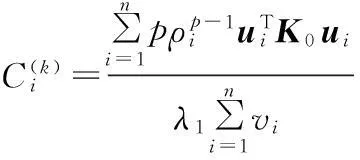
即材料被去掉一部分之后单元的ui发生了改变，这导致同一个单元的密度在迭代计算时趋向不同的结果。而计算前先按照使用要求把拓扑区域分成若干区间则保证了拓扑结果的可辨认性，提高了模型诠释过程的效率。

2.2基于拓扑计算的高强度螺栓优化布置

汽车结构中各总成之间一般采用螺栓连接，而且在受力复杂处应使用高强度螺栓代替普通螺栓以使车架受力均衡。但如果单独分析每个螺栓的受力将会耗费大量的时间，所以高强度螺栓的安装位置通常是工程师根据设计经验确定的，具有局限性。而基于拓扑计算的高强度螺栓位置确定方法将使这一过程快捷准确。图6为一示例分析模型。图6中先用四个位置约束了下层固定板6个方向的自由度，然后用bar单元模拟螺栓连接受力板，受力板在力的作用下会有沿着力方向运动的趋势，而此时各个螺栓的受力不完全相同。优化计算采用变密度法，设计变量为bar单元的材料密度，计算结果将把单元在[0,1]内的相对密度分为10个梯度并以不同的颜色标示出来(图中未能显示)。图中圆圈内的单元表示相对密度处于[0.9,1]之间的bar单元，也就是说该工况下这些螺栓的受力更大，那么在螺栓安装位置和直径不变的情况下，上述单元位置上的普通螺栓就应该换成高强度螺栓。

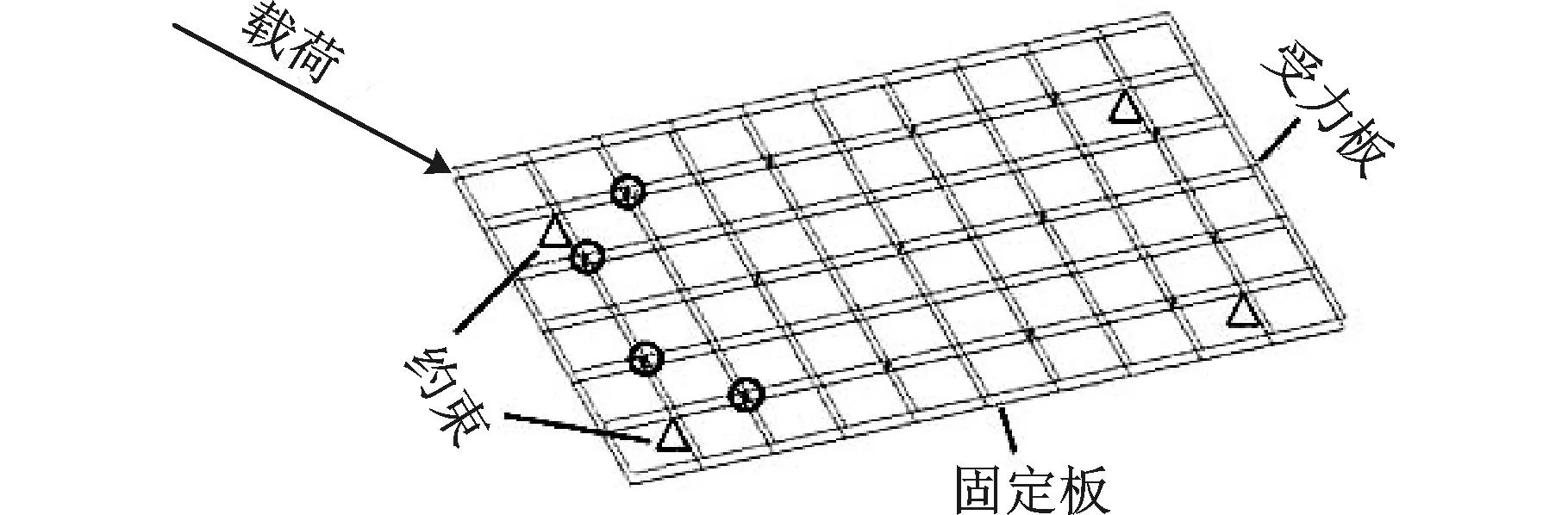
图6　示例分析模型及其优化计算结果

3　车架的轻量化设计

3.1模型概述

该轻量化设计使用的车架已应用于某型卡车上，但其初始设计质量过大，因此在其他结构不变的前提下对车架部分进行优化设计。图7为车架的原设计模型。模型主要包含a、b两根纵梁和5组横梁,每个横梁通过上下连接板与纵梁相连。此外，车架纵梁的尺寸规格已选定，因此优化设计只针对横梁区域。

1.一梁　2.二梁　3.三梁　4.四梁　5.五梁a-左纵梁　b-右纵梁图7　原车架模型

3.2车架结构设计

车架的刚度和强度是影响卡车运载能力的两大因素，而其模态的影响较小，因此从模型概念设计到尺寸定型的过程中主要考虑车架的刚度和强度性能。横梁的概念设计采用静态分析法，即在拓扑区间的受载位置施加车架所受载荷并在静载工况下进行计算。由优化方程的定义可确定设计变量、约束条件和设计目标，如表1所示。

表1　拓扑优化设置

车架轻量化设计后还将用于原车上，所以先在两纵梁间欲安装横梁的区域内设定拓扑区间填充网格单元，然后根据其他总成在车架上安装的大致位置把拓扑区间划分为五个小的部分，而为了尽量减少人为分割对拓扑结果产生的影响，各区间只隔开一个网格单元尺寸(10 mm)的距离即可，以保证计算后横梁间彼此位置的相对独立性，纵梁以及车架上其他部件保持不变，如图8所示。

A、B、C——三组车架轮心位置图8　车架拓扑区间划分

把设计区域和其他零件都划分为网格后(可忽略一些不重要的结构特征)，在车架上驾驶室、发动机变速箱、油箱和电瓶等位置处施加载荷。拓扑计算在车架的弯曲和扭转工况下进行，这是卡车车架在前期设计和后期校核中无论刚度还是强度都必须满足的静载荷工况。载荷方向均竖直向下，然后根据两工况的不同要求分别约束三组轮心A、B、C的自由度，拓扑计算的结果如图9所示。

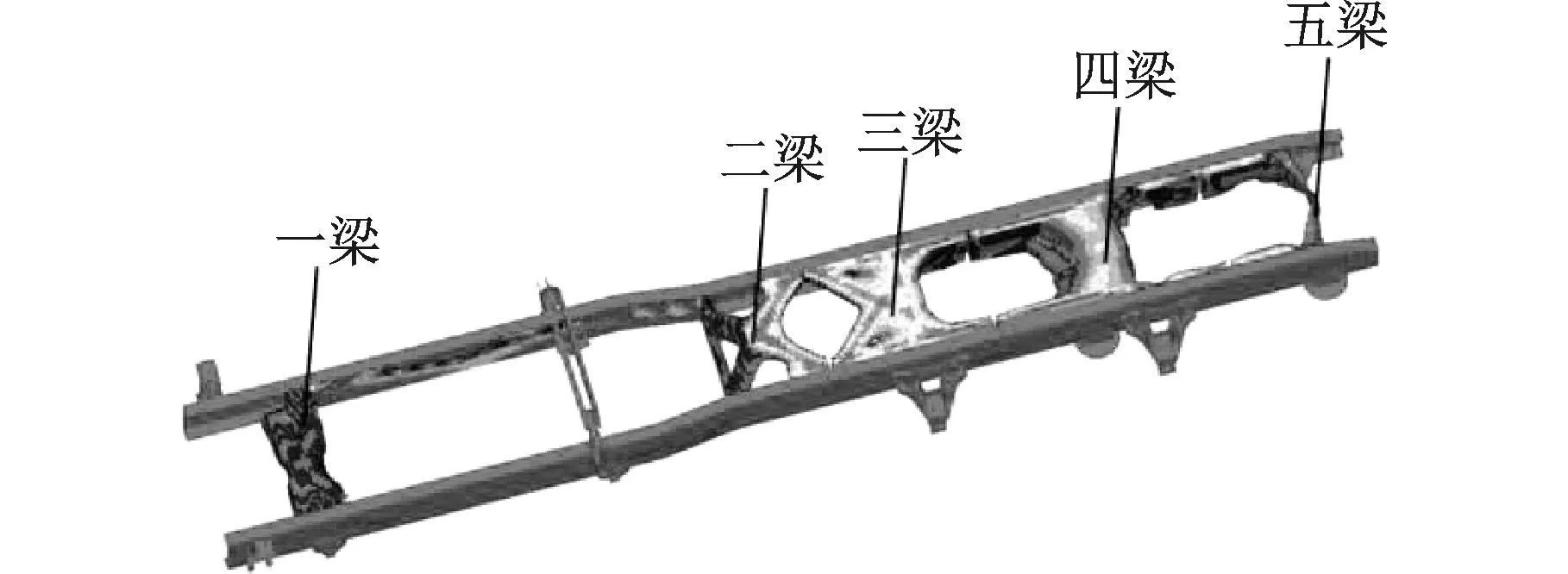
图9　车架拓扑计算结果

这一结果是计算车架中载荷的传递路径之后以材料密度的分布形式显示出来的，但它还不是车架的具体结构。根据计算结果可以直观确定横梁的长度及其在车架上的相对位置，而为了减少生产成本的重复投入以及保证新车架的性能变化不大，应参考现有的横梁模型确定其具体结构，然后在CAD软件中建立车架的三维模型(图10)。

1.一梁　2.二梁　3.三梁　4.四梁　5.五梁a-左纵梁　b-右纵梁图10　车架结构模型

3.3车架的尺寸设计

原车架在设计时为了拥有足够的刚度和强度，横梁截面的厚度尺寸相对较大，从而造成车架总质量过大。所以在保证其性能满足使用要求的同时，确定各个横梁的最小厚度是该车架轻量化设计的主要任务。在有限元计算中单元厚度等属性通常是以参数定义的，所以通过尺寸优化计算可以确定横梁截面的最佳厚度。

尺寸优化计算仍然在弯曲和扭转工况下进行。因为新车架各梁的变形和应力都应满足使用要求，所以约束条件分为刚度和强度两种情况，然后选取能同时满足两者的最佳厚度。尺寸优化的分析设置如表2。

表2　尺寸优化分析设置

横梁厚度值在优化减小后，车架的刚度和强度性能会相应变差，因此需在车架的实际工况条件下计算以保证优化结果的可用性。计算在optistruct中进行，新旧车架从前端到后端五组横梁和连接板的厚度对比结果如表3所示(数值作了圆整)。经轻量化指数式[8]计算可知：轻量化设计后车架的质量共减轻了10.16%，优化效果明显。

表3　尺寸优化结果

4　车架的校核分析

4.1刚度校核

车架横梁厚度值变小后能否满足原车的使用要求决定了优化设计的意义，因此，新旧车架刚度和强度的对比分析必不可少。刚度校核主要在车架的弯曲、扭转工况下进行，而且新旧车架的最大变形不能相差太大。两工况均约束三组轮心A、B、C的自由度，但具体要求不同，而且模型在同一工况下的处理方式应尽量一致以保证结果的可比性。新车架的载荷为其他总成所受到的重力，方向竖直向下，如图11所示。

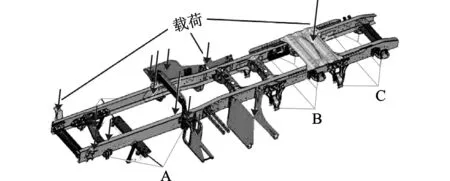
A、B、C——三组车架轮心位置图11　刚度校核加载

经Nastran计算可得表4中新旧车架在弯曲和扭转工况下刚度性能的对比结果。数据表明，两车架在这两个工况下的最大变形相差不大，新车架满足使用要求，优化结果可以接受。

表4　两车架Z向最大位移的对比数据

4.2强度校核

车架的强度校核将计算车架各梁所承受的最大应力并判断其危险位置。计算以von Mises应力为评价准则。车架各梁的材料参数如表5所示。

表5　车架各梁使用的材料参数　MPa

分析之后对于不允许出现变形失效的位置应参考材料的屈服强度，而不允许发生断裂的位置则参考材料的抗拉强度值来评价校核结果。强度校核时车架受到x、y、z三个方向的力，其加载情况如图12所示。计算工况以及相应工况下新旧车架最大应力的对比结果如表6所示。轻量化设计后车架在各工况下的最大应力普遍大于原车架的最大应力，尤其在扭转工况下，新车架纵梁的受力最大，但仍远小于材料的屈服极限，满足使用要求，其受力云图如图13所示。数据还说明了原车架设计时过大的强度裕度是车架过重的主要原因。

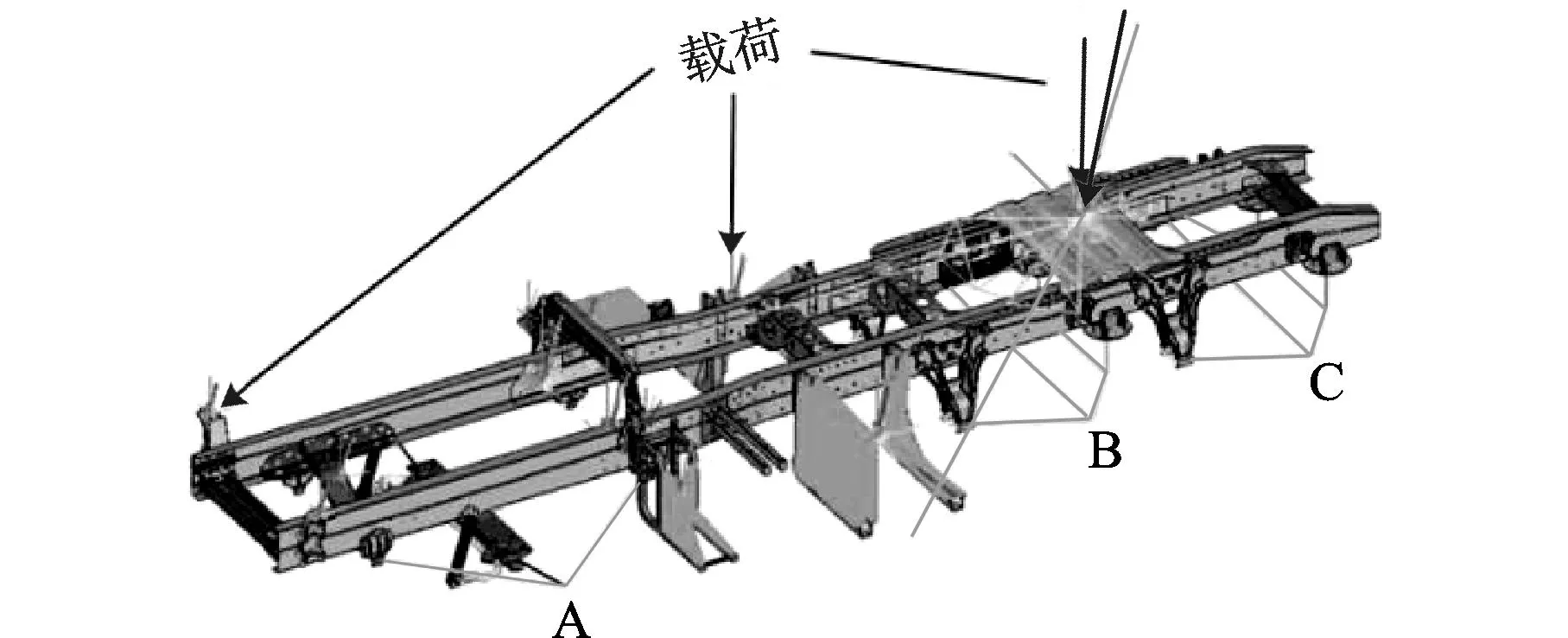
A、B、C——三组车架轮心位置图12　强度校核的加载工况

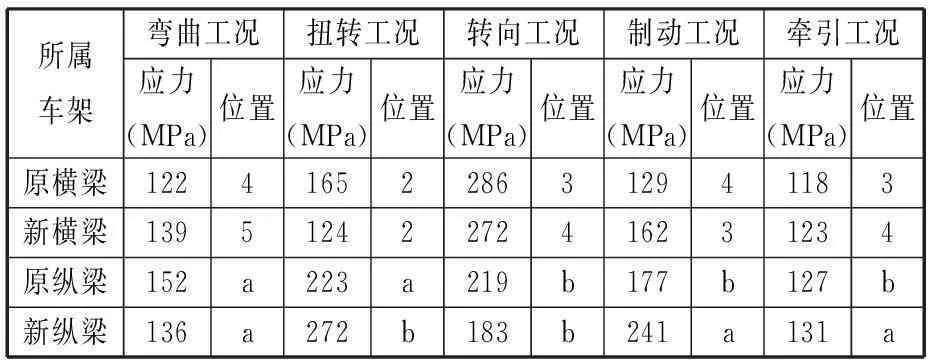
所属车架弯曲工况扭转工况转向工况制动工况牵引工况应力(MPa)位置应力(MPa)位置应力(MPa)位置应力(MPa)位置应力(MPa)位置原横梁12241652286312941183新横梁13951242272416231234原纵梁152a223a219b177b127b新纵梁136a272b183b241a131a

1.一梁　2.二梁　3.三梁　4.四梁　5五梁a-左纵梁　b-右纵梁图13　扭转工况的应力云图

5　高强度螺栓的优化布置

车架上不同位置螺栓的受力情况不完全相同，而一旦某个螺栓发生断裂失效，其周围的螺栓也将很快失效，因此必须把受力情况恶劣的普通螺栓更换为高强度螺栓。工厂中由于车间的模具要求、产品间通用性以及参考对标车等因素的限制，车架在设计之初就已经确定了螺孔位置和直径，所以令bar单元的属性与普通螺栓的参数相同并且在螺孔处连接各梁，螺孔处单元相对密度的拓扑计算在车架强度校核的各个工况下进行。拓扑优化的设置情况如表7，其中扭转工况下bar单元的拓扑计算结果如图14所示。图中圈出的bar单元表示扭转工况下这些螺孔处的螺栓受力较大，为使车架受力均衡应更换为高强度螺栓。综合所有工况后高强度螺栓的安装位置如图15中的圆点所示，共28处。

表7　bar单元的拓扑计算设置

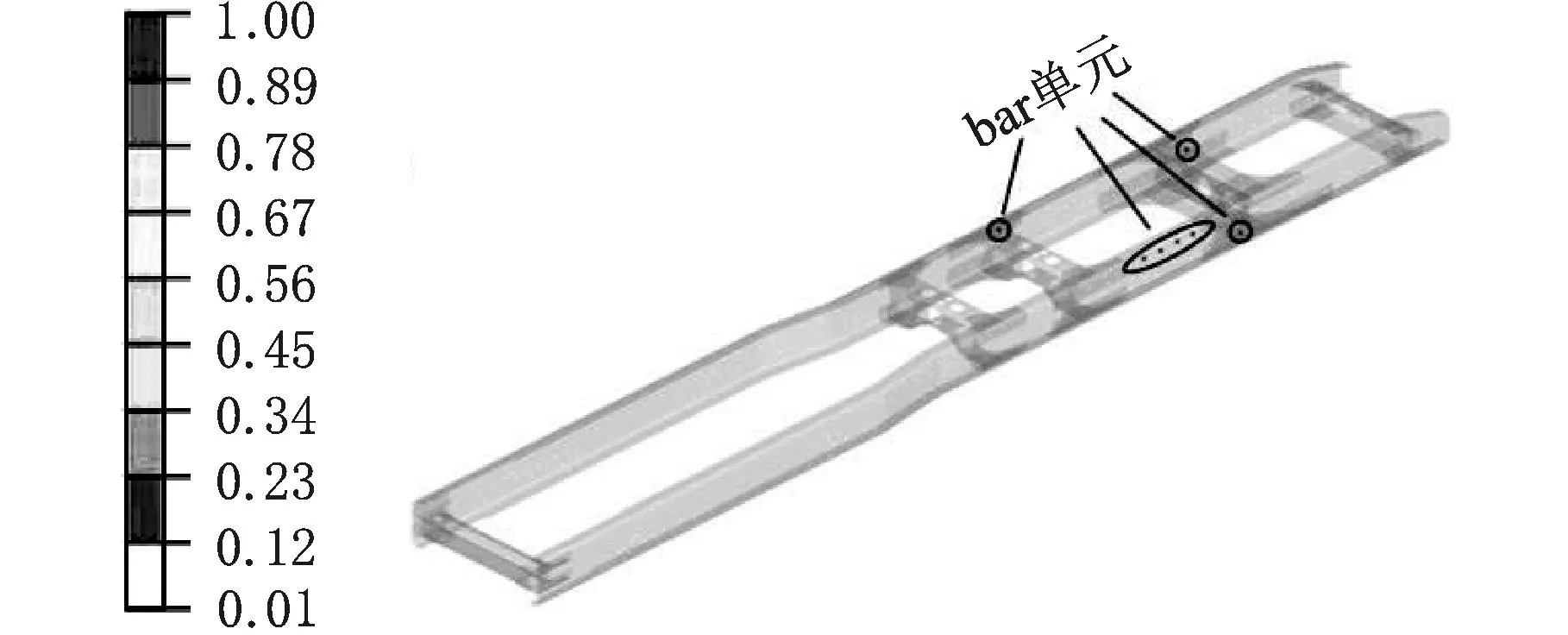
图14　扭转工况车架的单元拓扑结果

图15　高强度螺栓位置

6　实车试验验证

车架优化设计后的校核结果虽然满足要求但生产的实车能否满足使用要求还需要实车试验来验证。试验将直接使用据该轻量化方案生产的卡车样车。先在车架的测点位置上贴好应变片；再按要求进行试验并采集车架上的应变数据；最后把应变数据换算成应力数据并与仿真分析的结果进行对比。图16为应变片布置图，图17、图18是静态试验中测试值与仿真值的对比图。

图16　应变片粘贴位置

图17　静态弯曲试验的测试值与仿真值

图18　静载扭转试验的测试值与仿真值

动态应变测试的准备工作要求同上，驾驶卡车以相同的速度分别驶入不同类型的道路，如石块路、鹅卵石路等。试验结果说明，静态弯曲和扭转试验中测试值与仿真值匹配较好；动态试验中在未考虑附件自重的前提下，横梁及连接板的应力值较小,纵梁的最大应力值为263MPa，不超过材料的屈服极限，因此在测试路面条件下车架整体强度满足要求。此外试验更验证了模型分析的正确性与准确性，以及轻量化方案的可行性。

7　结论

(1)提出了基于区间分隔的拓扑优化法，使拓扑计算结果容易区分，有效地缩短了模型诠释过程的时间。

(2)在高强度螺栓位置确定问题上引入了拓扑优化方法，使螺栓的使用更加高效合理。

(3)轻量化方案包含了完整的前期模型概念设计与典型工况下的校核分析以及后期实车验证的对比分析，在保证其使用性能满足要求的前提下总质量降低10%以上，减重效果明显。

[1]韩旭，朱平，余海东,等. 基于刚度和模态性能的轿车车身轻量化研究 [J].汽车工程，2007，29(7)：545-549.

HanXu,ZhuPing,YuHaidong，etal.AStudyontheWeight-reductionofCar-bodywithRequiredStiffnessandModalPerformances[J].AutomotiveEngineering,2007,29(7): 545-549．

[2]ZhuP，ZhangY，ChenGL.Metamodel-basedLightweightDesignofanAutomotiveFront-bodyStructureUsingRobustOptimization[J].Proc.IMechE，PartD：J.AutomobileEngineering，2009，223：1-14.

[3]KodiyalamS，YangRJ，GuL,eta1.MultidisciplinaryDesignOptimizationofaVehicleSysteminaScalable.HighPerformanceComputingEnvironme-nt[J].StructuralandMultidisciplinaryOptimization,2004,26(3/4):256-263.

[4]施颐，朱平，张宇,等. 基于刚度与耐撞性要求的车身结构轻量化研究[J]. 汽车工程，2010,32(9):757-762.

ShiYi,ZhuPing,ZhangYu,etal.AStudyontheLightweightingofCarBodyStructureBasedonStiffnessandCrashworthinessRequirements[J].AutomobileEngineering，2010,32(9):757-762.

[5]刘为，薛克敏，李萍,等.汽车驱动桥壳的有限元分析和优化[J].汽车工程，2012,34(6)：523-527.

LiuWei，XueKemin，LiPing，etal.FEAnalysisandOptimizationofVehicleDriveAxleHousing[J].AutomotiveEngineering,2012,34(6): 523-527．

[6]张代胜，张林涛，谭继锦，等.基于刚度灵敏度分析的客车车身轻量化研究[J].汽车工程，2008,30(8)：718-720.

ZhangDaisheng,ZhangLintao,TanJijin,etal.AResearchontheLightweightingofBusBodyBasedonStiffnessSensitivityAnalysis[J].AutomotiveEngineering, 2008,30(8):718-720

[7]顾纪超，李光耀，干年妃,等.分步优化方法在后车架轻量化中的应用[J].汽车工程，2011，33(7)：641-644.

GuJichao，LiGuangyao，GanNianfei.ApplicationofStepwiseOptimizationtotheLightweightingofVehicleRearFrame[J].AutomotiveEngineering, 2011，33(7):641-644.

[8]马鸣图，路洪洲，李志刚.论轿车白车身轻量化的表征参量和评价方法[J].汽车工程，2009,31(5):403-406.

MaMingtu,LuHongzhou,LiZhigang.OntheDescriptionParametersandEvaluationMethodforLightweightingofCarBody-in-white[J].AutomotiveEngineering, 2009,31(5): 403-406.

(编辑卢湘帆)

Lightweight Design of a Truck Frame Based on Intervals

Hu Zhaohui1Zhang Jian1Li Guangyao1Yuan Zhijun2

1.State Key Laboratory of Advanced Desing and Manufacture for Vehicle Body,Hunan University,Changsha， 410082 2.SAIC GM Wuling Automobile Limited Ltd., Liuzhou, Guangxi, 545007

Topology optimization was the main method for the model conceptual design of a lightweight design. But the calculation results of the direct topology was usually chaotic for large models. So the topology space should be divided into several small areas in accordance with the operating requirements to make the results more clear. Based on topology calculation, the optimal placement method of the high strength bolts used bar elements to simulate bolts to calculate their relative densities. Then according to results, the position of high strength bolts in parts could be accurately determined. It is conducive for the rational use of high strength bolts. In the lightweight design process of a certain truck frame, the premise was to ensure the stiffness and strength performance to meet the demands of the typical working conditions from beginning to end. At the same time according to different design goals the design variables and constraints should be constantly adjusted and refined for the comprehensive applictions of topology optimization and size optimization. The final results show that after the optimization design the total mass reduces 60.4 kg. The effectiveness of weight loss is more than 10%.

lightweight; conceptual design; topological optimization; bolt optimization

胡朝辉，男，1981年生。湖南大学汽车车身先进设计制造国家重点实验室助理研究员。主要研究方向为汽车车身结构优化及其轻量化分析。张健，男，1987年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。李光耀，男，1963年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。袁智军，男，1966年生。上汽通用五菱汽车股份有限公司教授级高级工程师。

2015-03-31修回日期：2016-03-16

湖南省自然科学基金资助项目(13JJB003)

U270.32

10.3969/j.issn.1004-132X.2016.08.024