基于临界倾角约束的树形支撑结构生成算法

沈振宏　戴　宁　李大伟　吴长友

南京航空航天大学，南京，210016



基于临界倾角约束的树形支撑结构生成算法

沈振宏戴宁李大伟吴长友

南京航空航天大学，南京，210016

为节省三维打印的材料和时间，针对支撑结构体积优化的问题，提出了一种基于临界倾角约束的树形支撑结构生成算法。首先识别待支撑区域，并基于面积自适应采样获得待支撑点；再利用临界倾角约束进行树形结构节点的计算，并存储同一棵树上各节点的连接关系；采用扫掠和泊松曲面重建方法，生成树形支撑实体，最后通过实例进行了验证。实验结果表明，所提出的方法在保证打印稳定性的前提下，有效减少了支撑材料，缩短了打印时间。

三维打印；临界倾角约束；树形支撑；泊松曲面重建

0　引言

三维打印工艺过程中普遍存在着零件变形、翘曲、坍塌等问题。例如在SLM(selective laser melting)工艺过程中，热应力超过材料强度时发生的塑性变形以及逐层铺粉时的横向扰动等因素都会导致成形质量下降，因此需要设计支撑结构进行部分热量传导和零件固定。FDM(fused deposition modeling)工艺中，每个层面都是在上一层上堆积而成，上一层对当前层起到定位和支撑的作用。当前层的形状发生较大变化，如出现悬臂结构或较大倾斜面时，上层轮廓就不能给当前层提供充分的定位和支撑，这时就需要设计一些辅助结构用于支撑。因此，支撑结构的生成，是三维打印成形工艺中的一项关键技术。

支撑生成算法首先需要寻找模型中的待支撑部位。一类方法是先获得模型的分层轮廓数据，再利用分层数据进行识别。Chalasani等[1]对各层多边形进行合并，得到模型截面的最小包络矩形，进而得到模型的包围盒，该方法以SLC文件为输入，可以很快得到截面包络矩形的信息，但采用包围盒的方法，需要人工删除一些不需要添加支撑的区域。Huang等[2]自顶而下地对相邻两层实体切片进行求差、并的多边形布尔运算，算法有效利用了材料的自支撑能力，但是由于涉及到任意多边形的布尔运算和任意多边形的双向偏置，具有一定的复杂度，随着多边形和节点的增多，算法的耗时会显著增加。另一类方法是直接在三维模型上进行识别。Lan等[3]先对模型中待支撑的边进行处理，然后查找待支撑面片，该方法针对的模型相对简单，其适用范围具有一定局限性。Alexander等[4]将模型表面质量、加工时间、支撑体数量作为目标函数，通过求多目标问题的最优解集确定模型的分层方向。该算法采用参数肩高进行表面精度计算，并对肩高求值进行了优化，但是算法的时间复杂度较高。

对于支撑体的结构设计，最简单的方法是包围盒法，即求出模型的最小包络长方体。为了方便加工后支撑体的去除，Strano等[5]采用较稀疏的内部结构进行填充，Kritchman等[6]使用了可溶材料打印支撑体。但包围盒法没有考虑零件原型的形态特征，因此它也是一种最耗费支撑材料和成形时间的方法。为了减小包围盒法中支撑体的体积，陈岩等[7]采用直臂支撑结构，该算法能自动添加支撑点和支撑杆，但算法中的支撑传递参数无法自动选取，仅能通过实验估算。Huang等[8]提出了一种斜壁结构，该支撑结构分为三种类型，通过计算待支撑区域多边形的稳定系数，进而确定添加的支撑类型，但该算法减小的支撑体积有限，支撑与模型的接触面积较大。Dumas等[9]采用了一种桥梁支撑结构，该结构由一系列水平桥梁和竖直支柱构成，材料的耗费较少，但是该方法总体路线较为复杂，水平桥梁中锚线段的选取不明确。

本文提出一种基于临界倾角约束的树形支撑结构生成算法，该算法对于待支撑的点集，利用下层支撑点的临界倾角约束获得下层支撑点位置，构建节点结构体，生成树形结构，最后通过扫掠和泊松曲面重建生成树实体。

1　技术流程

基于临界倾角约束的树形支撑结构生成算法的技术流程如图1所示。首先识别模型中的待支撑区域，根据面片方向与加工方向(z轴正方向)的夹角保存模型中的待支撑面片，对待支撑面片集合进行相邻面片的合并，获得若干独立的待支撑区域。然后基于面积自适应采样获得待支撑点。之后，进入算法的核心部分，即利用临界倾角约束条件自上而下逐层生成树形支撑结构。以待支撑点为输入，利用下层支撑点的位置约束条件进行树形结构节点的计算，构建节点结构体，生成若干独立的树结构。最后，通过截面单元扫掠和泊松曲面重建生成支撑实体。

图1　基于临界倾角约束的树形支撑结构算法流程图

2　基于临界倾角约束的树形支撑结构生成

2.1待支撑区域识别

零件待支撑区域的自动识别，首先要读入零件的模型数据。三维打印系统多用STL格式文件表示零件的数据，即用大量的三角面片近似整个零件的表面。根据零件模型中面片方向与加工方向的夹角α与临界倾角β的大小关系，识别需要添加支撑的面片。α≤β时，由于材料自身的粘力作用，无需添加辅助支撑结构；α>β时，需要对面片添加支撑(图2粗实线区域)。同时对向下倾斜且不需要支撑区域的局部最低的点和边进行识别。

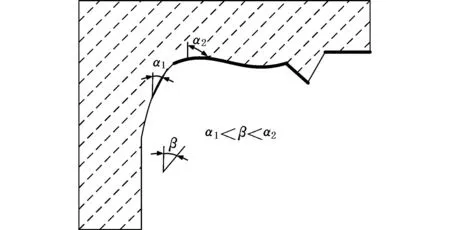
图2　待支撑区域识别

对于识别的待支撑面片集合Tsup，需要将集合中共边的面片进行合并，得到若干独立的待支撑区域A0，A1，…，An，面片合并结果为

(1)

Ai∩Aj=∅i，j=1，2，…，n且i≠j

算法采用区域增长法进行相邻面片的合并。首先任取集合中的一个面片作为种子，判断该种子的共边三角面片是否在集合Tsup中。若共边面片在集合中且未存为种子面片，则将其存到种子集中。继续寻找与其他种子共边的三角面片，直到种子集中的所有种子都查找过为止。重复上述步骤，完成各个区域的面片合并，流程如图3所示。

图3　相邻面片合并算法流程图

2.2基于面积自适应采样的待支撑点选择

获得待支撑区域后，需要在区域内采样一系列的待支撑点。算法首先获得区域投影的凸包，再对凸包进行栅格划分，根据栅格中面片的大小选取待支撑的点。

获得模型投影的凸包有两种方法。一种方法是先提取区域边界，再求边界点的凸包。边界提取，即先保存面域中的非公用边，得到组成边界的各条线段，再利用种子扩散法将相邻线段连接起来。另一种方法是直接将面域中的各顶点往某一平面投影，得到这些顶点投影的凸包。

得到投影的凸包后，采用一定的栅格间距d对凸包进行网格划分。栅格间距d的选取与材料的临界打印长度(材料在没有支撑的情况下保持不变形的极限打印长度)L有关。为了保证支撑的稳定性，同时避免选择的支撑点过于密集，选取经验值d=L/2。然后从栅格的左下顶点开始，逐行往上判断每个栅格中的顶点个数。当栅格中的点个数为0时，插入相应的点并保存；当栅格中的点个数大于1时，计算这些点的中心点并保存。最后通过射线求交，求得这些点在模型上的交点，得到一系列的待支撑点。

2.3基于临界倾角约束的支撑结构生成

获得待支撑点后，算法基于自上而下的生长策略，利用下层支撑点的临界倾角约束条件，生成树形支撑结构。对于待支撑点集P中的点p，假设通过下方的点s进行支撑，则向量sp与加工方向的夹角不大于临界倾角β。因此s可落于以点p为顶点、锥角为2β的圆锥体上或体内的任意位置。图4中，点p1、p2为零件原型上待支撑的点，c1为点p1对应的圆锥体，c2为点p2对应的圆锥体，则同时支撑p1和p2的下层节点可取圆锥体c1和c2相交区域中的任意点。本文选取该区域的最高点s，因为此时线段p1s、p2s的长度之和是最小的，即打印的支撑材料最少。

图4　锥约束求下层支撑点示意图

通过待支撑点的配对求交，并将交点插入到点集P中，直到点集P中所有点都计算过为止。该算法的输入为待支撑的点集P(按z从大到小存储)和以点集P中各点为顶点生成的对应的圆锥集C。整体支撑结构的生成通过遍历点p∈P和其对应的圆锥c∈C执行以下操作：

(1)查找圆锥c和模型m的最近交点sm，圆锥c与其他圆锥{ci|ci∈C且ci≠c}的最近交点；

(2)在圆锥c与其他圆锥{ci|ci∈C且ci≠c}的交点集合中，选择交点到相应两圆锥顶点p、pi距离之和L1最小的交点smin。如果线段psmin的长度大于线段psm的长度，删除点p和相应的圆锥c，保存线段psm，对下个点重复执行步骤1；

(3)将交点smin插入到点集P中，保存线段psmin、pismin；

(4)生成点smin对应的圆锥，删除点p、圆锥c和ci；

(5)当P非空时，对下一个点重复上述步骤。

通过配对求交获得树形结构中上下节点的连接关系，建立node结构体来存储树形结构中的各个节点，其定义如下：

Struct node

{intelement；

intlevel；

boolbvisit；

node*parent， lchild， rchild；

}

其中，成员变量element、level、bvisit分别为节点的索引值、节点在树结构中的层数、节点的访问标志，同时，每个节点还包含指向父节点和左右子节点的指针。通过node结构体将同一棵树上的节点关联起来，同时按照树结构层数从小到大的顺序逐层地把节点存在列表中。

2.4基于泊松曲面重建的支撑实体生成

2.4.1扫掠获得初始曲面顶点

得到树形支撑结构后，需要把它转化为实体，然后将带有支撑结构的原型零件转化为STL文件，经后续分层处理得到零件和支撑的截面轮廓，再对其进行路径规划，从而得到零件及支撑体的加工路径[10-11]。

算法通过分层保存的节点信息，使用水平截面单元逐层扫掠各层各节点到其子节点的路径，获得初始曲面顶点。然后对这些顶点进行编号和存储，生成网格曲面。此时生成的曲面在相交的区域没有进行相应的处理(图5三角形区域)，如果直接打印的话，将产生振动，影响打印的稳定性。

图5　扫掠示意图

2.4.2泊松曲面重建

由于扫掠生成的曲面是相互独立的，并且存在相交区域，因此需要对扫掠曲面进行曲面重建，使每棵树成为一个独立的整体。本文采用的泊松曲面重建方法[12]首先计算三维指标函数χ(点在模型内部时，χ=1；点在模型外部时，χ=0)，然后采用Marching Cubes算法提取一个适当的等值面来获得重建曲面。

重建算法首先计算模型的指标函数。指标函数的梯度是一个在表面附近非零，在其他任意位置都为零的向量场。因此，带法矢的表面点样本可以看作是指标函数梯度的样本。计算指标函数的问题因此可简化为梯度算子的反算，即找到标量函数χ，使其梯度最佳逼近由采样点定义的向量场V，即求minχ‖χ-V‖。如果采用散度算子，该问题就可以转化为一个标准的泊松问题，即计算拉普拉斯算子等于向量场V的散度的标量函数χ:

Δχ=·χ=·V

(2)

泊松曲面重建的重要步骤如下(重建结果如图6所示)：

(1)根据采样点的位置信息定义一个八叉树ϑ，然后给八叉树的每一个节点o∈ϑ，定义一个节点函数F0，之后定义函数空间fϑ,F≡Span{F0}，其结构类似于传统的小波表示；

(2)选择基函数F；

(3)定义向量场V；

(4)求解minχ‖χ-V‖的最小值；

(5)抽取等值面。

图6　泊松曲面重建示意图

另外，在进行泊松曲面重建之前，算法对树形支撑结构进行了局部优化：①在支撑结构与模型的接触区域，采用小圆接触。小圆的半径r=0.3 mm，圆平面法矢方向与待支撑点的法向量同向。采用小圆接触可以减小支撑体与模型表面的接触面积，方便后处理中支撑结构的剥离。②在支撑结构与底板的接触处采用较大的底面圆，底面圆半径为4.0 mm，从而更好地黏住底板，增加支撑结构稳定性。

3　实验结果与分析

3.1实验条件

提出的算法在MicrosoftVisualStudio2008软件开发平台上实现，并通过OpenGL进行模型显示。建模后的模型在美国MakerBot公司的MakerBotReplicator2打印机上完成打印，打印材料为ABS塑料丝，打印速度为40mm/s，移动速度为60mm/s，层高为0.2mm。

3.2临界倾角β标定实验

由于临界倾角β并不是一个定值，不同的打印机和打印材料对应的临界倾斜角可能不同。为此设计了不同倾角的树枝并进行实验，如图7所示。得到结果如表1所示，表1中的编号与图7的编号相对应。

图7　临界倾角标定试验

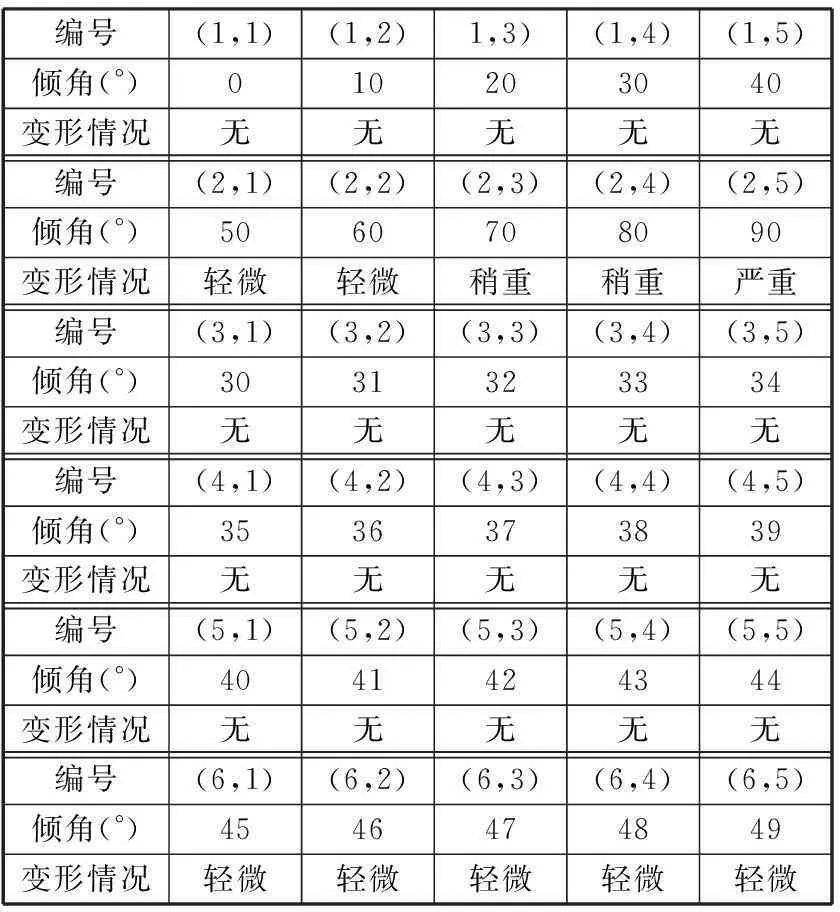
编号(1,1)(1,2)1,3)(1,4)(1,5)倾角(°)010203040变形情况无无无无无编号(2,1)(2,2)(2,3)(2,4)(2,5)倾角(°)5060708090变形情况轻微轻微稍重稍重严重编号(3,1)(3,2)(3,3)(3,4)(3,5)倾角(°)3031323334变形情况无无无无无编号(4,1)(4,2)(4,3)(4,4)(4,5)倾角(°)3536373839变形情况无无无无无编号(5,1)(5,2)(5,3)(5,4)(5,5)倾角(°)4041424344变形情况无无无无无编号(6,1)(6,2)(6,3)(6,4)(6,5)倾角(°)4546474849变形情况轻微轻微轻微轻微轻微

由表1可以看出，当倾角大于45°的时候，树枝开始发生变形，为了保证打印过程中的稳定性，保留一定的余量，取临界倾角β为40°。

3.3支撑建模及实验

获得了打印机对应的临界倾斜角β后，基于临界倾角约束逐层生成树形支撑结构的过程如图8所示，首先识别待支撑区域，然后基于面积自适应采样获得待支撑点，再根据下层支撑点的临界倾角约束计算树形结构中节点的位置，基于自上而下的生长策略生成树形支撑结构，最后通过泊松重建获得树形结构实体。

(a)识别待支撑区域　　　(b)计算待支撑点

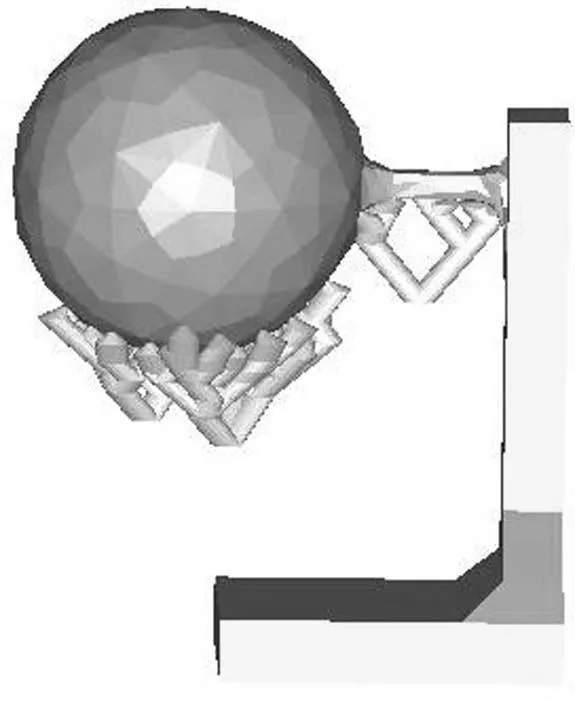
(c)生成支撑结构(状态1)　(d)生成支撑结构(状态2)

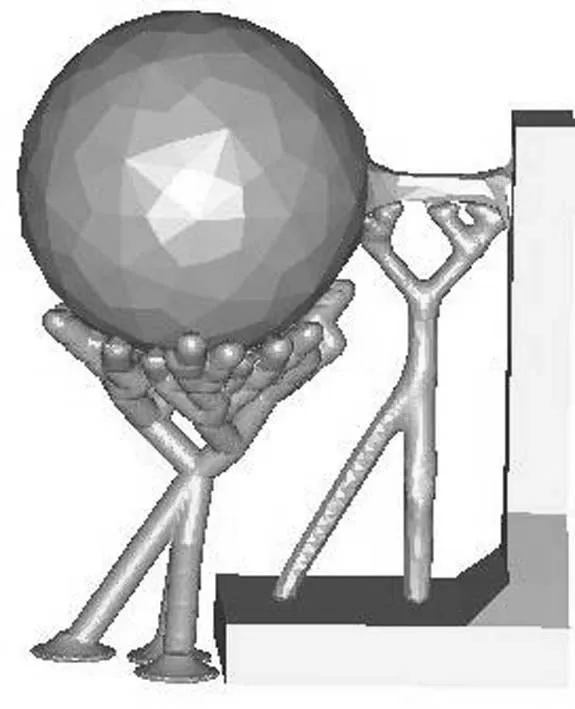
(e)生成支撑结构(状态3)　　(f)泊松重建生成实体

由于打印过程中存在扰动，影响树形结构整体的打印稳定性，因此算法对于图8e中的支撑结构底层进行了辅助支撑，再进行泊松曲面重建，得到图8f所示的结果。

为了客观评价提出的算法，将算法生成的支撑模型与打印机内置软件MakerWare和Magics RP v16.03(比利时Materialise公司)生成的支撑模型作对比，图9所示为悬吊球模型在不同方法支撑下的打印结果。图10所示为添加了树形支撑结构的牙颌托盘模型和人体骨头模型。3个模型的打印结果对比如表2所示。

(a)MakerWare　　　　　　　(b)Magics RP

(c)本文算法　　　　　(d)去除支撑后的模型图9　模型打印结果对比

图10　添加支撑后的牙颌托盘和骨头模型

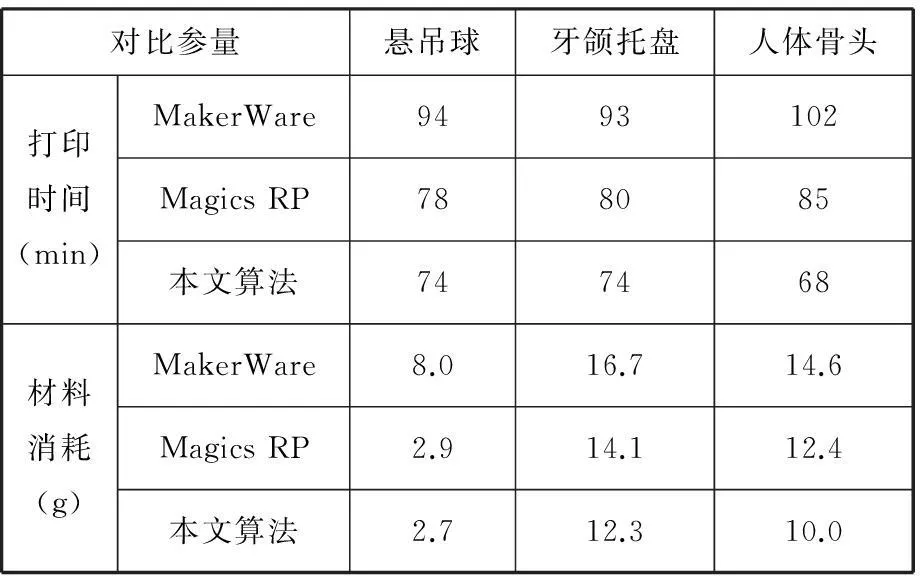
对比参量悬吊球牙颌托盘人体骨头打印时间(min)MakerWare9493102MagicsRP788085本文算法747468材料消耗(g)MakerWare8.016.714.6MagicsRP2.914.112.4本文算法2.712.310.0

由表2可以得出，相比MakerWare，本文算法降低了20%左右的时间消耗和近40%的材料消耗；相比Magics RP，本文算法在时间和材料耗费上也均占有优势。在模型表面成形质量方面，由于算法生成的支撑与物体模型的接触面积很小，所以生成的支撑对模型表面损害较小，同时降低了剥除支撑体的难度。

4　结论

(1)针对包围盒法和直臂支撑法生成的支撑结构体积大、打印时间较长的问题，提出一种基于临界倾角约束的树形支撑结构自动生成算法。算法利用下层支撑点的临界倾角约束条件，计算树形支撑结构节点的位置。

(2)针对支撑体生成、去除和支撑体稳定性的问题，本文通过扫掠获得初始支撑结构曲面，采用泊松曲面重建生成树形支撑实体。在支撑结构与模型的接触位置采用小圆接触的方式进行优化，同时对结构中承载较重的底部树干进行了辅助支撑。实验结果表明，该方法在保证模型原型正常打印的前提下，有效地减小了支撑体的体积和数量，同时缩减了打印时间。

(3)本文方法仍有不足之处，对于需要添加支撑的区域仍不能实现最小化，可能生成了一些额外的支撑。因此后续的研究重点是对区域的优化分析。

[1]Chalasani K，Jones L，Roscoe L. Support Generation for Fused Deposition Modeling[C]//Proceedings of Solid Freeform Fabrication Symposium. Austin：Texas，USA， 1995：229-241.

[2]Huang Xiaomao，Ye Chunsheng，Mo Jianhua，et al. Slice Data Based Support Generation Algorithm for Fused Deposition Modeling[J]. Tsinghua Science and Technology，2009，14(S1)：223-228.

[3]Lan Po-Ting，Chou Shuo-Yan，Chen Lin-lin，et al. Determining Fabrication Orientation for Rapid Prototyping with Stereolithography Apparatus[J]. Computer-Aided Design，1997，29(1)：53-62.

[4]Alexander P，Allen S，Dutta D. Part Orientation and Build Cost Determination in Layered Manufacturing[J]. Computer-Aided Design，1998，30(5)：343-356.

[5]Strano G，Hao L，Everson R，et al. A New Approach to the Design and Optimization of Support Structures in Additive Manufacturing[J]. Advanced Manufacturing Technology，2013，66(9/12)：1247-1254.

[6]Kritchman E，Gothait H，Miller G. System and Method for Printing and Supporting Three Dimensional Objects：US，7364686[P]. 2008-04-29.

[7]陈岩，王士玮，杨周旺，等. FDM三维打印的支撑结构的设计算法[J]. 中国科学，2015，45(2)：259-269.

Chen Yan，Wang Shiwei，Yang Zhouwang，et al. Construction of Support Structure for FDM 3D Printers[J]. Scientia Sinica，2015，45(2)：259-269.

[8]Huang Xiaomao，Ye Chunsheng，Wu Siyu，et al. Sloping Wall Structure Support Generation for Fused Deposition Modeling[J]. Advanced Manufacturing Technology，2009，42(11/12)：1074-1081.

[9]Dumas J，Hergel J，Lefebvre S. Bridging the Gap：Automated Steady Scaffolding for 3d Printing[J]. ACM Transactions on Graphics，2014，33(4)：1-10.

[10]卞宏友，刘伟军，王天然. 基于STL模型支撑算法的研究[J]. 机械设计与制造，2005(7)：49-52.

Bian Hongyou，Liu Weijun，Wang Tianran. Study on Algorithm for Generate Support Based on STL File[J]. Machinery Design & Manufacture，2005(7):49-52.

[11]洪军，王崴，张宇红. 光固化快速成形自动支撑技术研究[J]. 机械工程学报，2004，40(11)：134-138.

Hong Jun，Wang Wei，Zhang Yuhong，et al. Research on Auto-support in Stereolithography[J]. Journal of Mechanical Engineering，2004，40(11):134-138.

[12]Kazhdan M，Bolitho M，Hoppe H. Poisson Surface Reconstruction[C]//Proceedings of the fourth Eurographics Symposium on Geometry Processing. Aire-la-Ville，Switzerland：Eurographics Association，2006：61-70.

(编辑张洋)

Generation of Branching Support Structures Based on Critical Angle Constraint

Shen ZhenhongDai NingLi DaweiWu Changyou

Nanjing University of Aeronautics & Astronautics，Nanjing，210016

In order to optimize support structures’ volume, and save the material and printing time, an automatic generation algorithm was proposed based on critical angle constraint. Firstly, the algorithm detected areas that required support, and the support points were obtained by adaptive sampling based on the area. Secondly, through critical angle constraint, the nodes in branching support structures were calculated, and all nodes information in a tree were saved. Finally, the resulting structure was obtained by the sweep surface after Poisson reconstruction. The algorithm was evaluated by experiments, and the experimental results demonstrate that the algorithm provides a reliable method to ensure the printing stability as well as reducing the printing material and time.

3D printing; critical angle constraint；branching support；Poisson surface reconstruction

沈振宏，男，1990年生。南京航空航天大学机电学院硕士研究生。主要研究方向数字化设计与制造、三维打印技术。戴宁(通信作者)，男，1978年生。南京航空航天大学机电学院副教授。李大伟，男，1989年生。南京航空航天大学机电学院硕士研究生。吴长友 ，男，1989年生。南京航空航天大学机电学院硕士研究生。

2015-06-15

国家高技术研究发展计划(863计划)资助项目(SS2013AA040802)；江苏省科技支撑项目(BE2014009-3)；航空科学基金资助项目(20151652024)；江苏省三维打印装备与制造重点实验室开放课题资助项目(BM2013006)

TH164

10.3969/j.issn.1004-132X.2016.08.020