小型异构件抛光机运动系统分析

刘建春　陈雄风　廖妮兰

1.厦门理工学院，厦门，361024　　2.厦门万久科技有限公司，厦门，361015



小型异构件抛光机运动系统分析

刘建春1陈雄风1廖妮兰2

1.厦门理工学院，厦门，3610242.厦门万久科技有限公司，厦门，361015

为解决小型异构件全自动抛光机在抛光复杂曲面零件时夹具体相对于布轮位姿的精确控制难题，基于抛光机结构，分析其三直线轴和三旋转轴的运动系统，建立机台的D-H坐标系。通过运动学正反向运算推导出其位姿方程并求得逆解，确定夹具体位姿与各个关节变量的对应关系。以水龙头为例，提取三维模型表面关键点坐标，借助MATLAB和ADAMS逆解出各关节变量数值，实现各关节的运动学仿真。抛光实验获得的表面粗糙度Rz=0.36 μm，满足抛光要求。

机器人；抛光机；运动学仿真；小型异构件

0　引言

长期以来，国内解决复杂曲面抛光问题的方法主要是手工抛光。近年来，企业逐渐采用抛光机器人或抛光数控机床来加工门把手、水龙头等异型工件。准确抛光各类异型曲面零件，需要五轴及以上联动控制。多轴联动加工中，离线编程成为制约加工效率提高的主要环节，而多轴联动机床的运动学研究为解决离线编程核心算法提供重要理论依据。Yang等[1]根据螺旋理论提出了一种能避免产生奇异点的刀具路径轨迹生成算法，但他们并未对如何根据刀具路径轨迹生成机床各轴运动轨迹的方法进行研究。Gallardo等[2]针对不同结构形式的机器人提出了一种模块化的空间超冗余度运动学模型(包括位置速度和加速度分析)，但研究对象只局限于串联机械手。王朋等[3]运用齐次坐标变换理论和Preston方程，建立了机械手抛光的材料去除数学模型，并运用所建立的数学模型进行确定性抛光试验，但其研究主要针对材料去除特性，对抛光轨迹与机械手各轴间的运动关系研究较少。宋孟军等[4]通过建立冗余坐标系的方法，简化了运动学建模及求解的过程，但其同样未对机械手运动轨迹与位姿间的关系进行研究。

上述研究主要针对串并联机械手抛光，对专用抛光机的研究也局限于自由度较少的机床，针对多轴联动布轮抛光机的研究则鲜有报道。在大量的布轮抛光设备中，由于无法准确建立工件与布轮间的运动学关系，故而不得不采用示教方法编写抛光程序，这严重制约着抛光效率的提高。

本文以六轴小型异构件布轮抛光机运动系统为研究对象，建立了抛光机的运动学模型；提取工件三维模型表面关键点坐标，利用多项式拟合成样条曲线；结合运动学逆解求出抛光轨迹上各点所对应的机床各关节变量值；利用虚拟样机技术进行运动学仿真，并结合抛光试验验证运动学模型的准确性。

1　小型异构件抛光机机构分析

1.1抛光机床的技术要求

针对异型复杂曲面零件的加工需求，小型异构件抛光机工作台具备X、Y、Z方向的3个直线自由度，以确保布轮能够接触到工件表面的任意位置。加工过程中，为保证工件表面法线方向与布轮半径方向相重合，在抛光机工作台上安装了由3个旋转关节构成的机械手，以调整布轮与工件表面的姿态。

1.2抛光机机械结构介绍

如图1所示，抛光布轮安装在机台Z轴上，由变频电机带动旋转。三轴机械手安装在工作台上，夹持工件贴靠在Z轴布轮上进行抛光加工。小型异构件抛光机械手的运动由中臂、小臂和夹具体的回转组成。机械手的结构决定了抛光加工的运动模式，3个关节的旋转角度决定了工件相对于抛光布轮的姿态。中臂、小臂和夹具体的旋转运动均由伺服电机带动的谐波减速器来实现，其中，夹具体的转动是通过同步带将减速器的转动传动到夹具体心轴上来实现的。通过X、Y和A、B、C五轴联动可实现小型异构件复杂表面的抛光。

1.抛光布轮　2.工件　3.小臂　4.X轴移动平台　5.Y轴移动平台　6.大臂　7.中臂　8. Z轴平台图1　抛光机台运动系统结构

2　抛光机台运动学方程的推导

根据D-H法[5-6]，对图1所示的抛光机结构建立坐标系，如图2所示，其中，OWXWYWZW是工件坐标系，OTXTYTZT是布轮坐标系，O1X1Y1Z1、O2X2Y2Z2、O3X3Y3Z3、O4X4Y4Z4、O5X5Y5Z5、O6X6Y6Z6分别为床身坐标系、Y轴坐标系、X轴坐标系、大臂坐标系、中臂坐标系、小臂坐标系，其中，小臂坐标系O6X6Y6Z6与工件坐标系OWXWYWZW重合。相应D-H参数如表1所示。

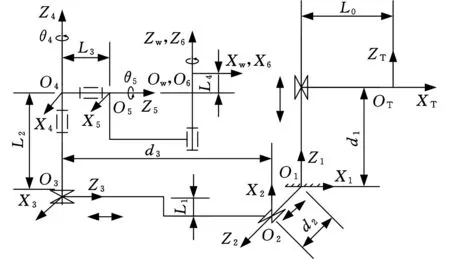
图2　抛光机各关节坐标系

关节i连杆夹角αi-1连杆长度ai-1连杆距离di连杆扭角θi10°L0-d10°290°0d290°390°L1d390°490°0L2θ45-90°0L3θ5690°0L4θ6

按照齐次坐标变换的方法建立相邻两个坐标系之间的变换矩阵[7-8]。TT1代表O1X1Y1Z1坐标系在OTXTYTZT坐标系中的位姿描述，以此类推，其中，ci=cosθi，si=sinθi。

(1)

(2)

(3)

(4)

(5)

(6)

则从工件坐标系到布轮坐标系总的变换矩阵为

TTW=TT11T22T33T44T55TW

(7)

变换矩阵TTW是所有关节变量的函数，已知各关节变量的数值便可求出工件坐标系相对于布轮坐标系的位姿。

离线编程过程中，可通过工件表面若干关键点坐标拟合出局部曲面方程，根据曲面方程确定工件坐标系与布轮坐标系的位姿关系，进而通过机器人运动学逆解求出各关节变量的对应值，以驱动各关节电机按照一定的角速度与角加速度旋转。小型异构件空间曲面方程可表示为

F(x，y，z)=0

(8)

抛光加工过程中，在布轮与工件接触点处建立布轮坐标系OTXTYTZT，被加工点P在工件坐标系OWXWYWZW下的坐标为(xP，yP，zP)，在P点建立坐标系OPXPYPZP，其中，ZP方向为该点法线方向，YP方向为该点沿抛光轨迹的切线方向，如图3所示。

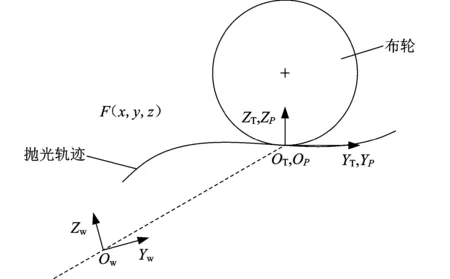
图3　抛光位姿图

当抛光到P点时，P点法线通过布轮中心，即布轮坐标系OTXTYTZT与该点坐标系OPXPYPZP重合，此时在工件坐标系中对曲面方程求各变量关于P点的偏导数即可得到P点的法向量n：

n=(fx，fy，fz)

(9)

以y为变参数，通过求x、y、z三个参数对y的导数即可得到P点沿抛光轨迹方向的切向量(YP的方向向量)τ的表达式：

τ=(0，1，-fy/fz)

(10)

结合式(9)、式(10)，根据向量间的乘法，即可确定XP的方向向量o：

(11)

坐标系OPXPYPZP在工件坐标系OWXWYWZW中的位姿描述可用齐次矩阵表示为

(12)

其中，WxP为XP轴分别与XW、YW、ZW轴夹角的余弦值组成的三维向量，同理可得WyP、WzP的含义，WlP为OP相对于OW的位置向量。

以求XP轴与XW轴的夹角余弦值为例进行说明：

(13)

式中，a为XW的方向向量，a=(1,0,0)。

为了简化位姿表达式，令

同理可得其余坐标轴夹角余弦值，进而确定WTT的表达式：

(14)

xP、yP、zP分别为P点在工件坐标系OWXWYWZW中的坐标。而TTW=(WTT)-1，根据机器人运动学逆解将式(7)两边同乘以(TT1)-1，得

(TT1)-1TTW=1T22T33T44T55TW

(15)

使式(15)两边元素分别相等，可求出关节变量d1的表达式，以此类推，有

(1T2)-1(TT1)-1TTW=2T33T44T55TW

(2T3)-1(1T2)-1(TT1)-1TTW=3T44T55TW

⋮

从而可解得各关节变量表达式。

3　基于MATLAB和ADAMS的运动学联合仿真

在建立抛光机机构运动学模型后，利用MATLAB和虚拟样机软件ADAMS进行运动学仿真。

本次运动学仿真主要模拟抛光工件以特定位姿和轨迹相对于布轮运动时，各关节的运动情况。以抛光水龙头曲面为例，首先在CAD软件中提取三维模型曲面上的部分关键点，再将这些关键点拟合为多项式样条曲线，曲线模型如图4所示。

图4　水龙头表面拟合曲线

根据各关键点坐标，利用式(10)、式(11)所示的运动学逆解方法在MATLAB中求出各关节变量位移。逆解过程中，利用反正切值求3个旋转关节的角度会遇到多解的情况，因此限制3个回转轴的活动范围为-π～π，并且指定各轴沿位移变化较小的方向旋转到计算位置[9]。在ADAMS软件中，将逆解求得的各关节位移值拟合成样条曲线，驱动各关节运动，设置仿真时间为5 s，步数为1000。仿真结束后，得到夹具体末端在布轮坐标系下的运动轨迹，与水龙头三维模型表面提取的曲线形状一致，证明了运动学模型的准确性。X、Y、Z轴位移变化曲线如图5所示，A、B、C轴角度变化曲线如图6所示。

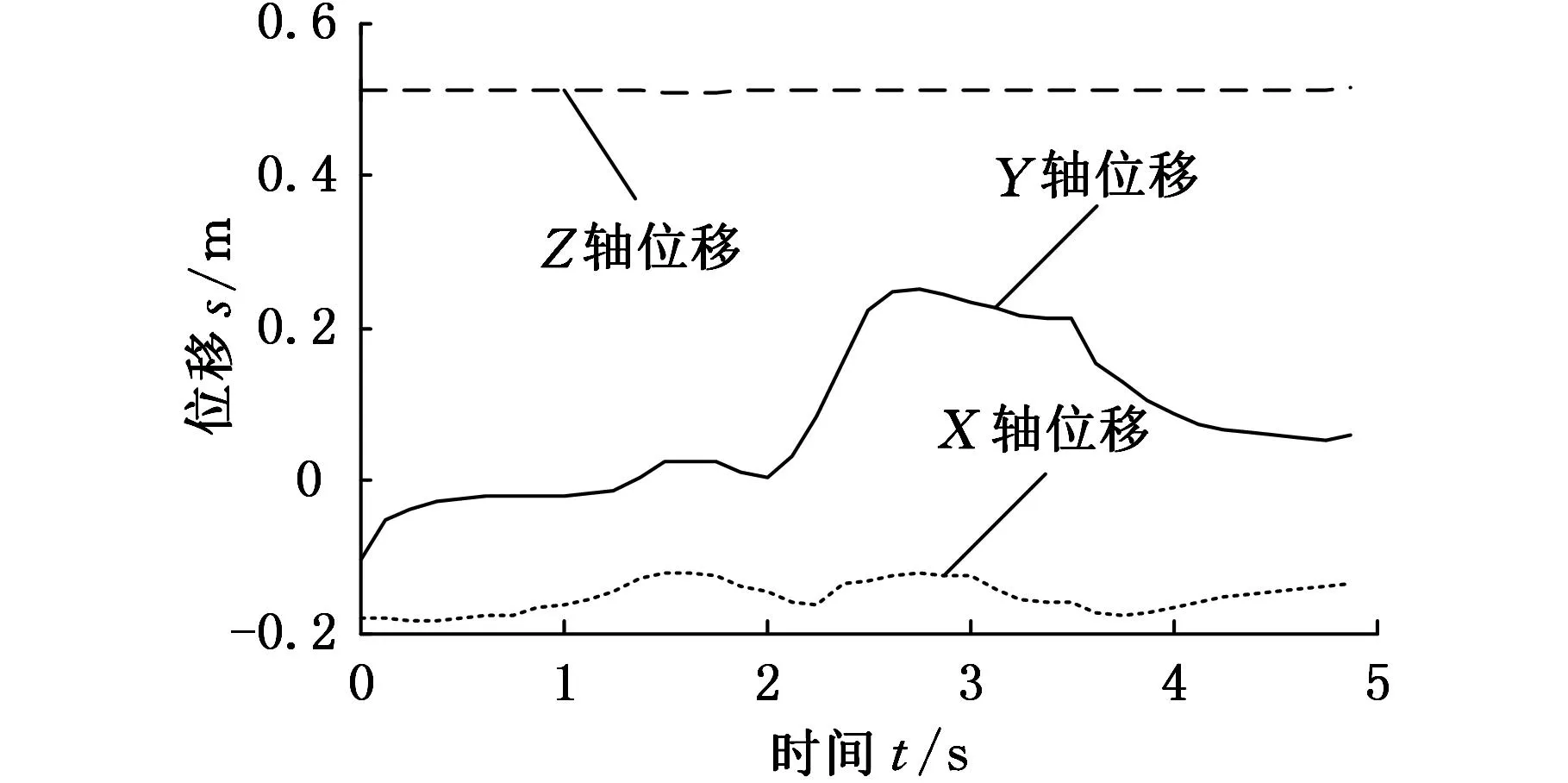
图5　直线关节位移曲线图

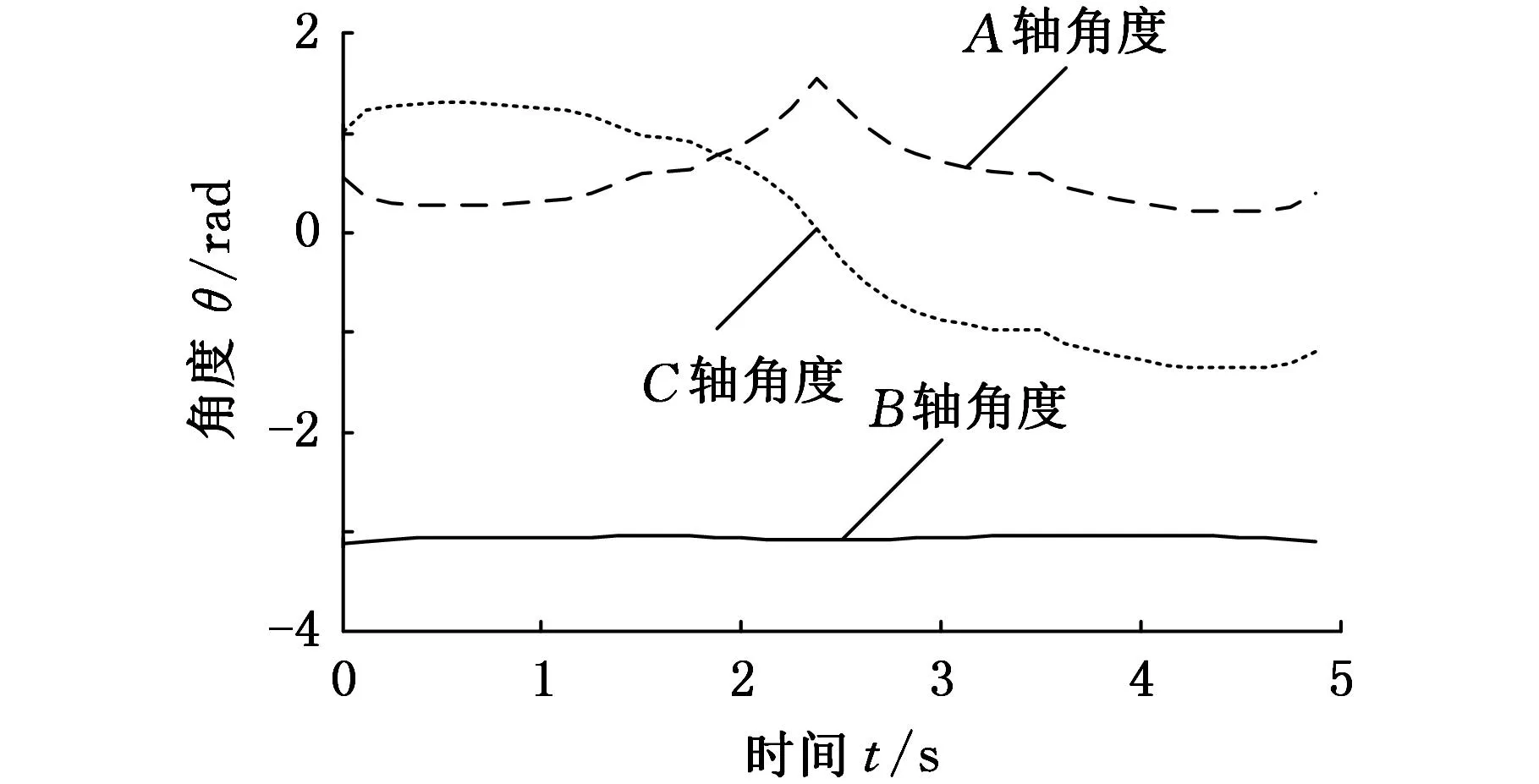
图6　旋转关节转角曲线图

由图5、图6可以看出，抛光机在X、Y轴方向上位移变化幅度较大，这与提取的水龙头表面曲线相符。抛光过程中，主要通过A轴和C轴控制曲线法线方向，B轴转动量相对较小。各轴的位移、角度变化均匀、连续，符合设计要求。

4　水龙头试件抛光试验

为了验证上述运动学分析的准确性，将各轴逆解得到的位移值转换为NC代码，对水龙头进行抛光。然后采用泰勒霍普森表面粗糙度轮廓仪检测抛光后的水龙头表面粗糙度，获得轮廓偏距R与取样长度L的关系，如图7所示，在长度L为30 mm的曲线轮廓上，轮廓最大高度Rz=0.36 μm，轮廓算术平均偏差Ra=0.04 μm，满足抛光加工效果要求。

图7　水龙头抛光后表面粗糙度曲线

5　结语

本文分析了抛光机运动结构，建立了运动学模型，根据各关节位移量推导出工件坐标系相对于布轮坐标系的位姿。在工件坐标系与布轮坐标系相对位姿确定的情况下，可求得各关节的位移，实现抛光轨迹的控制。在此基础上设计出的六轴五联动抛光机床达到小型复杂曲面零件的抛光加工要求。

[1]YangJixiang,AltintasY.GeneralizedKinematicsofFive-axisSerialMachineswithNonsingularToolPathGeneration[J].InternationalJournalofMachineTools&Manufacture, 2013, 75(12):119-132.

[2]GallardoJ,LessoR,RicoJM,etal.TheKinematicsofModularSpatialHyperredundantManipulatorsFormedfromRPS-typeLimbs[J].Robotics&AutonomousSystems, 2011, 59(1):12-21.

[3]王朋，陈亚，宣斌，等.大口径光学元件的机械手抛光[J].光学精密工程，2010，18(5)：1077-1085.

WangPeng,ChenYa,XuanBin,etal.PolishingLargeApertureMirrorsbyManipulator[J].OpticsandPrecisionEngineering, 2010, 18(5)：1077-1085.

[4]宋孟军，张明路，张建华.一种新型移动机器人运动学坐标系快速构建方法研究[J].中国机械工程，2011，22(17)：2017-2021.

Song Mengjun, Zhang Minglu, Zhang Jianhua. Research on Rapid Construction Method of Kinematics Coordinate System from a New Kind of Mobile Robot[J]. China Mechanical Engineering, 2011, 22(17):2017-2021.

[5]杨玉维，赵新华，孙启湲，等.基于多体动力学特性的机械手时间最优轨迹规划[J].机械工程学报，2014，50(7)：8-13.

Yang Yuwei, Zhao Xinhua, Sun Qiyuan, et al. Trajectory Optimization of Manipulator for Minimum Working Time Based on Multi-body Dynamic Characters[J]. Journal of Mechanical Engineering, 2014, 50(7):8-13.

[6]张智，邹盛涛，李佳桐，等.六自由度机械手三维可视化仿真研究[J].计算机仿真，2015，32(2)：374-377.

Zhang Zhi, Zou Shengtao, Li Jiatong, et al. Three-Dimensional Visual Simulation Research on Six Degrees of Freedom Manipulator[J]. Computer Simulation, 2015, 32(2):374-377.

[7]刘极峰，丁继斌.机器人技术基础[M].北京：高等教育出版社，2012.

[8]闫继宏，郭鑫，刘玉斌，等.一种模块化机械臂的设计与运动学分析[J].哈尔滨工业大学学报，2015，47(1)：20-25.

Yan Jihong, Guo Xin, Liu Yubin, et al. The Design and Kinematic Analysis of a Modular Manipulator[J]. Journal of Harbin Institute of Technology, 2015,47(1):20-25.

[9]Xi Weitao, Remy C D. Optimal Gaits and Motions for Legged Robots[C]//International Conference on Intelligent Robots and Systems. Chicago, 2014: 3259-3265.

(编辑张洋)

Motion System Analysis of Small Heterogeneous Parts Polishing Machine

Liu Jianchun1Chen Xiongfeng1Liao Nilan2

1.Xiamen University of Technology，Xiamen，Fujian，361024 2.Xiamen Winjoin Technology Ltd., Xiamen，Fujian，361015

In a small heterogeneous parts automatic polishing machine(SHPAPM), it was significant to precisely control the relative motion between a clamp and a cloth wheel, especially for polishing of complex surface parts. Based on the structure of SHPAPM, the motion system with 3 linear axes and 3 rotational axes was analyzed, and the DH machines coordinate system was established. In the coordinate system, pose’s equations were deduced from kinematics forward and reverse operations, then their inverse solutions were obtained. Those solutions determined mapping relationship between clamp poses and robot’s joints. For verification, a faucet 3D surface model was applied to justify the new method in a MATLAB/ADAMS based simulator. In the simulation, the new method successfully solves unknown variables for joints. Besides simulation, field polishing experiments were also conducted, which results in low roughness(Rz=0.36 μm) and high accuracy.

robot; polishing machine; kinematics simulation; small heterogeneous parts

刘建春，男，1972年生。厦门理工学院机械与汽车工程学院教授。主要研究方向为机器人、数控系统的控制与应用。发表论文30余篇。陈雄风，男，1990年生。厦门理工学院机械与汽车工程学院硕士研究生。廖妮兰，女，1975年生。厦门万久科技有限公司高级工程师。

2015-06-09

福建省科技计划资助重点项目(2012H0042)；厦门市科技计划资助项目(3502Z20131156)

TG659

10.3969/j.issn.1004-132X.2016.08.008