多质量特性产品参数设计灰靶模型
2016-08-16李亚平刘思峰方志耕陈洪转
李亚平 刘思峰 方志耕 陈洪转 徐 兰
1.南京林业大学,南京,210037 2.南京航空航天大学,南京,2100163.英国De Montfort大学,莱斯特,LE1 9BH 4. 江苏科技大学,镇江,212003
李亚平1刘思峰2,3方志耕2陈洪转2徐兰4
1.南京林业大学,南京,2100372.南京航空航天大学,南京,2100163.英国De Montfort大学,莱斯特,LE1 9BH4. 江苏科技大学,镇江,212003
提出一种多质量特性的产品参数选择灰靶模型来辅助工程设计者进行决策。结合正交试验设计,针对多质量特性产品参数选择的具体问题,研究了灰靶模型的要素及相互间关系;提出一组改进型田口质量损失函数,并将其损失值作为灰靶模型效果的基本测度。该模型能兼顾设计过程中的内外影响因素,判断出可取和不可取的参数组合,从而确定方案的满意区域;根据效果测度值可以确定多质量特性产品的最优参数水平组合。
多质量特性;参数选择;灰靶;田口质量损失函数;正交试验
0 引言
工程设计中,为解决多质量特性产品参数选择问题,人们研究了稳健设计、不确定优化设计、结构优化设计等设计方法[1-9]。这些设计方法的核心思想是在现有技术水平、资源约束以及设计目标和要求等的基础上,探求一个相对满意的方案,这与灰靶模型的基本思想一致。灰靶模型[10]本着灰色系统理论中非唯一性原则,在优化意义下的满意区域寻求一个相对最优的方案。考虑灰靶模型中各要素的性质和相互间关系,利用灰靶模型进行多质量特性产品参数选择,能够兼顾设计过程中的内外影响因素,并发现可取和不可取参数组合,可辅助工程设计者确定方案的满意区域。因此,运用灰靶模型进行多质量特性产品参数选择是值得研究和探索的。
利用灰靶模型进行多质量特性产品参数选择的一个重要内容就是如何测度效果值。田口质量损失[11-12]是一种较好的衡量产品质量好坏的指标,但其存在以下不足:①没有考虑特性的量纲;②总是将不可能实现的望大特性无穷大值和望小特性无穷小值作为理想值是有失偏颇的;③望目特性的函数忽略了质量损失不对称的事实。因此,本文提出一组改进型田口质量损失函数,并以此作为灰靶决策效果测度的基本工具。另外,考虑到正交试验设计[12]是考虑设计过程中内外影响因素的一种重要方法,以此为基础,针对多质量特性产品参数选择的具体问题,设计了灰靶模型的各要素及其之间的关系,并以改进型质量损失函数为效果测度值,判断出设计过程中的可取和不可取参数组合,并通过比较测度值的大小,确定相对最优参数水平组合,解决了多质量特性产品参数选择问题。该方法简洁明了,易于操作,能够辅助工程设计者进行决策。
1 问题描述
1.1田口质量损失函数
田口博士认为,产品上市后的质量波动性会给企业带来一定的损失,由产品质量问题导致的损失被称为质量损失,并将田口质量损失函数作为度量质量损失的工具[2]。质量损失函数的通用模型为
L(y)=K(y-y0)2
(1)
式中,K为质量损失系数,是不依赖于y的常数;y为质量特性值,y0是其目标值。
y离y0越近,L(y)值越小,表明设计的质量损失小,功能质量好。
1.2正交试验设计
正交试验是安排多因素试验、寻求最优水平组合的一种经济、高效、快速的试验方法[13]。试验过程如下:确定试验的可控因素和噪声因素及其水平表;选择合适的正交表(内表和外表),设计内表和外表试验方案;根据试验目的,确定试验指标;进行试验并分析试验结果,确定最佳因素水平组合。
1.3灰靶模型
灰靶模型决策的四要素是事件、对策、目标和效果。
(1)事件集与对策集。某一决策问题研究范围内事件的全体称为该问题的事件集,记为A={a1,a2,…,an},其中,ai(i=1,2,…,n)表示第i个事件。相应的所有可能的对策全体称为对策集,记为B={b1,b2,…,bm},其中,bj(j=1,2,…,m)表示第j种对策。
(2)局势集。事件集A与对策集B的笛卡儿积A×B={(ai,bj)|ai∈A,bj∈B}称为局势集,记作S=A×B。若ai∈A,bj∈B,则(ai,bj)为局势,记为sij=(ai,bj)。
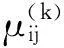
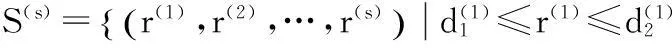
(2)
为s维决策灰靶。
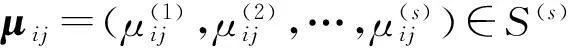
决策灰靶实质上是相对优化意义下满意效果所在的区域。在决策问题中,很多情境下要取得绝对的最优是不可能的,因而人们往往退而求其次,要求有个满意的结果就行,即要求局势sij的目标效果向量满足
那么,sij即为“中靶”局势。
2 改进型田口质量损失函数
不同质量特性的意义、量纲和性质可能各不相同,为在建模与计算时得到具有可比性的质量损失测度,设计一组改进型田口质量损失函数,即标准质量损失函数。根据质量指标的不同特性可以获得标准质量损失函数的设计对象,包括望大质量特性、望小质量特性和望目质量特性.
定义1标准质量损失是指质量特性值与其目标值的量纲一偏差程度。设质量特性值为y,L(y)为其标准质量损失,则有:
(1)设y为望大质量特性,其标准质量损失函数为
(3)
式中,y*为y的最小可接受值;y′为y的最大可达值;K为质量损失系数,K≤1。
(2)设y为望小质量特性,其标准质量损失函数为
(4)
式中,y**为y的最小可达值;y″为y的最大可接受值。
(3)设y为望目质量特性,其标准质量损失函数为
(5)
式中,yc为y的目标值;y-为y的最小可接受值;y+为y的最大可接受值;α为yc≤y 定义1中的质量损失系数可以通过专家定性给出,或者通过经典方法计算后,作变换处理,视具体情况而定。 与传统的田口质量损失函数相比,标准质量损失函数有如下优势:①归一化;②望大质量特性最大可达值、望小质量特性最小可达值的引入弥补了特性值无穷大和无穷小均不可实现的不足;③望目质量特性引入两种质量损失系数更符合质量损失不对称的实际情况;④标准质量损失函数比传统质量损失函数更经济可行。运用标准质量损失函数计算的结果能够初步去掉一部分不可取的方案,即损失值为1的方案均不可取,而传统质量损失函数需要根据具体情况设置阈值,推广性较弱。 定义2设A为事件集,B为对策集,S为局势集,则称 (6) 为局势集S在k目标下的一致效果测度矩阵。 定义4设A为事件集,B为对策集,则称 (7) Uj=(μ1,μ2,…,μm) (8) 为对策集B的综合效果测度向量。 推论3综合效果测度μj满足以下条件:①量纲一;②效果越理想,μj越小;③μj∈[0,1]。 目标1,2,…,s的s维决策灰靶为 对于局势sij中靶的情形,可以通过比较综合效果测度μj的大小判断对策bj的优劣。 4.1基本原理 利用定义1~定义6及推论1~推论3找出最小的综合效果测度所对应的对策bjo,即解决了参数选择问题。 4.2多质量特性产品参数选择灰靶模型设计算法步骤 在上述分析的基础上,基于正交试验的多质量特性产品参数选择灰靶模型的实现步骤如下: (1)确定正交试验指标,即确定质量特性集Y; (2)确定需要设计的参数{x1,x2,…,xp}、噪声因素{o1,o2,…,oq}及其水平表; (3)选择合适的正交表(内表和外表),设计内表试验方案m组、外表试验方案n组; (4)进行试验并记录试验结果。 (5)计算一致效果测度矩阵 某离合器系统是一个多功能整合系统,为使这个离合器系统正常工作,扭矩必须保持稳定,且体现离合器传递扭矩能力的后备系数必须大于1。要达到上述设计要求,必须考虑8个参数(表面光洁度、原料、润滑油、C.E.半径、指针半径、齿轮角度、齿轮高度和齿轮厚度)的选择问题。利用文中提出的方法进行参数选择。 (1)确定目标,即质量特性:扭矩(y1)、后备系数(y2)。 (2)确定需要设计的参数、噪声因素及其水平表。需要设计的参数:表面光洁度(x1)、原料(x2)、润滑油(x3)、C.E.半径(x4)、指针半径(x5)、齿轮角度(x6)、齿轮高度(x7)和齿轮厚度(x8),噪声因素:温度(n1)和老化程度(n2)。两者的水平安排如表1、表2所示。 表1 设计参数(可控因素)水平表 表2 设计参数(可控因素)水平表 (3)内表选择L18(21×37),共18组试验方案;外表选择L4(22),共4组试验方案。 (4)进行试验并记录结果,如表3所示。 表3 正交试验结果 (6)根据一致效果测度矩阵,剔除“脱靶”局势对应的对策。若y1和y2目标下存在一致效果测度值为1的局势,则该局势脱靶,对应的对策为不可取对策,剔除对策b3、b6、b7、b8、b10、b11、b13、b14。 0.1522,∞,∞,0.2406,∞,∞,0.2586,0.1925,0.1908,0.2417) ∞,0.1231,0.0625,0.0394,∞,∞,0.0112,∞, 0.0264,0.0548,0.0499,0.1288,0.0476) (8)计算对策集B的综合效果测度向量Uj。目标y1、y2的决策权均为0.5,对策集B的综合效果测度向量为 Uj=(0.0653,0.1293,∞,0.2338,0.1006,∞,∞,∞,0.0958, 多质量特性产品参数选择问题的解决思路与灰靶模型的基本思想一致,而且正交试验设计是兼顾设计过程中内外影响因素的一种重要工具,针对参数选择的具体问题,设计了灰靶模型的各要素及其之间的关系。将改进型田口质量损失函数作为灰靶模型效果的基本测度工具,与传统田口质量损失函数相比,改进型田口质量损失函数有三点优势:①量纲一化;②望大质量特性最大可达值、望小质量特性最小可达值的引入,分别弥补了特性值无穷大和无穷小均不可实现的不足;③望目质量特性引入两种质量损失系数更符合质量损失不对称的实际情况。该灰靶模型能够兼顾设计过程中的内外影响因素,判断出可取和不可取参数组合,可辅助工程设计者确定方案的满意区域,并可通过比较效果测度值大小确定相对最优参数水平组合,解决了多质量特性产品参数选择问题。该方法清晰明了,易于操作,能够辅助工程设计者进行设计决策。 [1]张根保,任显林,刘立堃,等. 面向制造过程的产品多关键质量特性优化模型[J].计算机集成制造系统,2010, 16(6): 1286-1291.ZhangGenbao,RenXianlin,LiuLikun,etal.MultipleKeyQualityCharacteristicsOptimizationModelforManufacturingProcess[J].ComputerIntegratedManufacturingSystems, 2010, 16(6):1286-1291. [2]耿金花,高齐圣,张嗣瀛. 多因素、多指标产品系统的建模与优化[J].系统工程学报, 2008, 23(4): 449-454. GengJinhua,GaoQisheng,ZhangSiying.ModelingandOptimizationofMulti-factorandMulti-indexProductSystem[J].JournalofSystemsEngineering, 2008, 23(4): 449-454. [3]KöksoyaO.ANonlinearProgrammingSolutiontoRobustMulti-responseQualityProblem[J].AppliedMathematicsandComputation, 2008, 196(2): 603-612. [4]SunGY,LiGY,GongZH,etal.MultiobjectiveRobustOptimizationMethodforDrawbeadDesigninSheetMetalForming[J].Materials&Design, 2010, 31(4): 1917-1929. [5]PickleSM,RobinsonTJ,BirchJB,etal.ASemiparametricApproachtoRobustParameterDesign[J].JournalofStatisticalPlanningandInference, 2008, 138(1): 114-131. [6]杨方,高齐圣,于增顺. 多响应问题的稳健性设计优化[J]. 工业工程, 2010, 13(3): 43-46. YangFang,GaoQisheng,YuZengshun.RobustDesignOptimizationofMulti-responseProblems[J].IndustrialEngineeringJournal, 2010, 13(3): 43-46. [7]何桢,马彦辉,赵有. 基于田口过程能力指数和熵权理论的多响应稳健优化设计[J]. 中国农机化, 2008(3): 33-36. HeZhen,MaYanhui,ZhaoYou.RobustDesignOptimizationofMulti-responseBasedonTaguchiProcessCapacityIndexandEntropyTheory[J].ChineseAgriculturalMechanization, 2008(3): 33-36. [8]乔红威,吕震宙,李洪双. 基于随机响应面法的响应灵敏度分析及稳健优化设计[J]. 中国机械工程, 2009, 20(3): 337-341. QiaoHongwei,LüZhenzhou,LiHongshuang.ResponseSensitivityAnalysisandRobustDesignBasedonStochasticResponseSurfaceMethod[J].ChinaMechanicalEngineering, 2009, 20(3): 337-341. [9]李亚平,刘思峰,方志耕,等. 基于质量特性与参数隐式函数关系的DEA混合稳健设计模型[J]. 中国机械工程, 2012, 23(9): 1079-1083. LiYaping,LiuSifeng,FangZhigeng,etal.AHybridRobustDesignModelbyDEAforImplicitFunctionofQualityCharacteristicsandItsParameters[J].ChinaMechanicalEngineering, 2012, 23(9): 1079-1083. [10]LiuY,JeffreyF,LiuSF.Multi-objectiveGreyTargetDecision-makingBasedonProspectTheory[J].Control&Decision, 2013, 28(3):345-350. [11]葛健全,贾天宝,赵志明,等. 基于田口方法的弹道修正弹参数优化[J]. 弹箭与制导学报,2008,28(6):211-214. GeJianquan,JiaTianbao,ZhaoZhiming,etal.OnParametersOptimizationofTrajectoryCorrectionSubmunitionUsingTaguchiMethod[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2008, 28(6):211-214. [12]李波.空间润滑谐波减速器传动性能正交试验分析[J]. 机械工程学报,2012,48(3):82-87. LiBo.OrthogonalExperimentAnalysisonTransmissionPerformanceofSpaceLubricatedHarmonicDrive[J].JournalofMechanicalEngineering, 2012,48(3):82-87. [13]陈建江,钟毅芳,肖人彬. 基于正交试验的稳健优化设计方法及其工程应用[J]. 中国机械工程, 2004, 15(4):283-286. ChenJianjiang,ZhongYifang,XiaoRenbin.DesignMethodofRobustOptimizationBasedonOrthogonalTestsandItsApplication[J].ChinaMechanicalEngineering, 2004,15(4):283-286. (编辑张洋) Grey Target Model for Parameter Design of Multi-quality-characteristic Products Li Yaping1Liu Sifeng2,3Fang Zhigeng2Chen Hongzhuan2Xu Lan4 1.Nanjing Forestry University, Nanjing, 210037 2.Nanjing University of Aeronautics and Astronautics, Nanjing, 210016 3.De Montfort University, Leicester, UK, LE1 9BH 4.Jiangsu University of Science and Technology, Zhenjiang, Jiangsu, 212003 A grey target model for parameter choice of multi-quality-characteristic products was proposed to aid engineering designers to make decisions. Based on orthogonal experimental design, elements and relationships among them of the grey target model were studied for the parameter choice of multi-quality-characteristic products. A group of improved Taguchi quality loss functions were developed, and their values were thought to be the basic measures for the effects in the grey model. The internal and external factors were considered simultaneously in the design process. According to the effect value, acceptable parameter combinations were distinguished from unacceptable ones to get a satisfactory domain for design. Moreover, based on the effect value, the optimal parameter combination for multi-quality-characteristic products can be obtained. multiple quality characteristics;parameter choice;grey target;Taguchi quality loss function;orthogonal experiment 李亚平,女,1985年生。南京林业大学经济管理学院讲师。主要研究方向为质量管理与工程。发表论文10余篇。刘思峰,男,1955年生。南京航空航天大学经济与管理学院教授、博士研究生导师,英国DeMontfort大学researchprofessor。方志耕,男,1962年生。南京航空航天大学经济与管理学院教授、博士研究生导师。陈洪转,女,1977年生。南京航空航天大学经济与管理学院教授、博士研究生导师。徐兰,女,1982年生。江苏科技大学经济管理学院讲师。 2015-6-18 欧盟第七研究框架计划玛丽·居里国际人才引进计划Fellow项目(FP7-PIIF-GA-2013-629051);国家社会科学基金资助重点项目(12AZD102);国家自然科学基金资助项目(61301108,71403109,71372080);国家级教学团队基金资助项目(10td128);教育部人文社科青年基金资助项目(14YJC630151);中央高校基本科研业务费专项资金资助项目(NP2014105,NP2015208);江苏省高等学校哲学社会科学重点研究基地资助项目(2014JDXM015) F273.2; N941.5 10.3969/j.issn.1004-132X.2016.08.015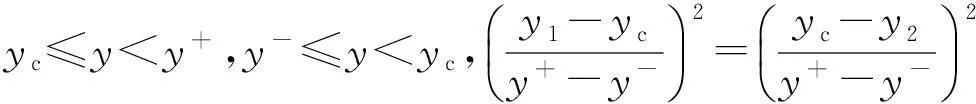
3 效果测度
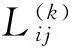
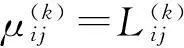

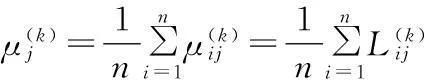
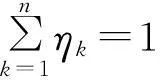

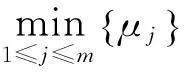
4 基于正交试验设计的多质量特性产品参数选择灰靶模型
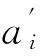

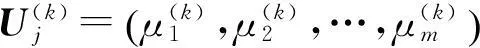
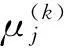
5 实际应用

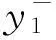
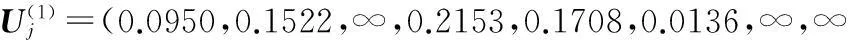
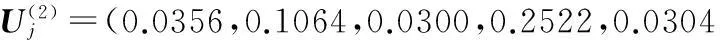

6 结语
