含磁滞补偿的电液伺服系统预设性能跟踪控制

董振乐　马大为　姚建勇　王晓锋

南京理工大学，南京，210094



含磁滞补偿的电液伺服系统预设性能跟踪控制

董振乐马大为姚建勇王晓锋

南京理工大学，南京，210094

针对电液伺服系统普遍存在的参数不确定性、不确定非线性(磁滞、摩擦、外干扰等)，提出一种基于自适应鲁棒控制的含磁滞补偿的预设性能跟踪控制策略。以阀控单出杆液压缸位置伺服系统为例，首先建立了含磁滞非线性的系统数学模型，然后通过定义预设性能函数，实现了对跟踪误差收敛速率、最大超调量和稳态精度的预先规划，基于规划后的转换误差设计了自适应鲁棒控制器，并提高了稳态和瞬态跟踪性能。仿真对比结果表明：该控制策略可以减小磁滞对系统跟踪精度的影响，提高跟踪误差的收敛速度，减小最大超调量，最终实现优良的跟踪性能。

电液伺服系统；磁滞；预设性能控制；建模不确定性；自适应鲁棒控制

0　引言

电液伺服系统具有功率密度大、响应快、输出力/力矩大等突出优点，在工业和国防领域得到了广泛的应用[1-2]。然而电液伺服系统存在的参数不确定性(如伺服阀的流量增益、液压油的体积模量、液压缸的泄漏系数等)和不确定非线性(如未建模外干扰、非线性摩擦、磁滞等)给控制器的设计带来了很大难度。

自适应控制是针对参数不确定的常用技术手段[3]，可以有效地估计系统未知参数和可参数化的系统不确定非线性并实现较好的模型补偿，但对不可参数化的不确定非线性无能为力。针对不确定非线性，可采用滑模控制[4]、鲁棒控制[5]、神经网络控制[6]等方法处理。

以上控制方法，常常只关注系统的稳态跟踪性能，对于跟踪误差超调量、收敛速度等瞬态指标，却很少涉及。实际系统运行时，一旦出现超调量过大、收敛过慢等不理想状况，系统性能必然受损，严重时甚至造成执行器失效。针对此类问题，Rovithakis等[7]提出了预设性能控制，即通过定义预设性能函数，对系统跟踪误差的超调量、收敛速度等瞬态性能指标以及跟踪精度等稳态指标施加约束，通过误差转换，将原始受限的跟踪误差转换为新的设计误差，并基于此进行了控制器的设计，保证了系统的稳态性能和瞬态性能。需要说明的是，文献[7]中预设性能函数的定义是独立于控制器设计的，这极大地方便了预设性能控制与其他高性能控制器的结合，从而在许多系统中得到了较好的应用[8]。

此外，某些液压元器件(电液伺服阀中的力矩马达、压电直驱伺服阀中的压电材料等)普遍存在磁滞特性，它极易导致系统在低频时的相位滞后[9]，影响控制器的最终性能。针对此类问题，文献[10]将磁滞特性建模为线性项和有界干扰项的组合，该模型简单，给磁滞补偿控制器的设计提供了便利，也在许多领域得到了应用[11]。文献[12]提出一种基于磁滞逆模型的磁滞补偿方法，然而相比于文献[10]所述方法，该方法稍显复杂。

本文以某阀控单出杆液压缸位置伺服系统为例，首先建立了包含磁滞非线性[11]的系统数学模型，在模型中同时考虑系统参数不确定性和不确定非线性。然后在自适应鲁棒控制的基础上，融合预设性能控制，不但获得了较好的稳态跟踪性能，而且保证了预先设定的瞬态性能指标。最后通过仿真验证了控制器的有效性。

1　含磁滞非线性的系统建模

1.1磁滞模型

由于传统间隙类磁滞模型的不连续特性对非线性系统的控制器设计十分不利，故本文根据文献[10]，给出如下磁滞模型：

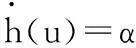
(1)

式中，u、h(u)分别为磁滞模型的输入(控制输入)和输出；α、c、B1为磁滞参数，均为常数，c>B1。

式(1)所描述磁滞特性曲线如图1所示，磁滞模型参数c=1.3，B1=0.9，α=10。

图1　磁滞特性曲线

求解式(1)可得[10]

h(u)=cu(t)+dh(u)

(2)

式中，h(u0)、u0分别为h(u)和u的初值。

分析式(2)易知，转换后的磁滞模型由斜率为c的线性项和非线性干扰项dh(u)组成。对于dh(u)项，由文献[10]可得如下结论：

进一步分析式(2)易知，干扰项dh(u)指数收敛至相应界值。在下一步液压系统的建模中，式(2)中的磁滞模型将会考虑在内，同时将基于该磁滞模型进行磁滞特性补偿。

1.2液压系统非线性数学模型

本文中的单出杆液压缸位置伺服系统原理如图2所示，伺服阀控制液压缸直接驱动惯性负载做直线运动。根据牛顿第二定律，惯性负载动力学方程为

(3)

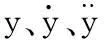
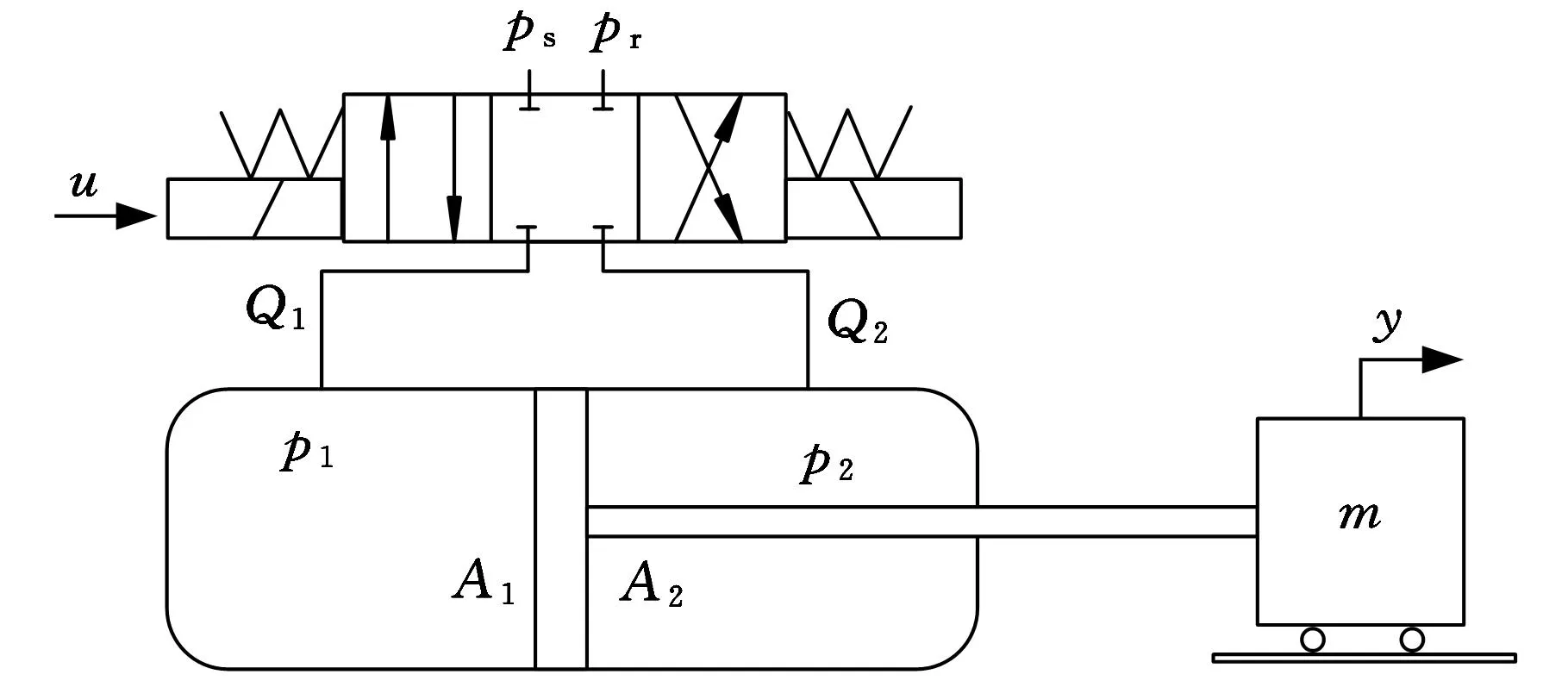
图2　阀控单出杆液压缸位置伺服系统原理示意图

执行器两腔压力的动态方程为[9]

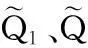
由文献[9]可知，负载流量QL和伺服阀阀芯位移xv的关系为

(5)

式中，Cd为伺服阀节流孔系数；w为伺服阀节流孔面积梯度；ρ为液压油密度；ps为系统供油压力；pr为系统回油压力，pr=0。

由于伺服阀的频宽远大于系统工作时的频宽，因此建模时我们忽略伺服阀的动态过程[13]，将阀的控制输入和阀芯位移视为比例环节，即xv=kih(u)，其中，ki为电压-阀芯位移的增益系数，则式(5)转化为

(6)

定义状态变量

同时结合式(3)～式(6)，并代入式(2)可得系统总数学模型：

(7)

θ1=B/mθ2=Af/mθ3=ckvK/m

g=A1R1/V1+A2R2/V2

f2=(A1/V1+A2/V2)pL

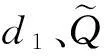
2　预设性能控制器设计

2.1预设性能函数

定义跟踪误差e=x1-x1d，假设其需满足以下性能指标：

-δlρ(t)0

(8)

其中，δu、δl为正的设计参数，用于辅助约束跟踪误差的上下限；ρ(t)为正的递增光滑函数[8]：

ρ(t)=(ρ0-ρ∞)e-kt+ρ∞

其中，ρ0、ρ∞和k均为正的可设计参数；-δlρ0、δuρ0分别约束了误差的最大下冲量和最大超调量。参数k可调节跟踪误差的收敛速度，ρ∞可调节跟踪误差的稳态界。显然，式(8)对跟踪误差的性能给出了具体的规划。为了便于后续控制器的设计，定义如下递增函数[9]：

(9)

分析易知，式(9)等价于e(t)=ρ(t)S(z1(t))，且z1(t)有界时，预设性能式(8)始终满足。

选取的递增函数S(z1)：

(10)

求取式(10)的反函数，可得

(11)

接下来针对转换误差z1进行控制器设计。

2.2控制器设计

对式(11)求导可得

(12)

进一步可得

(13)

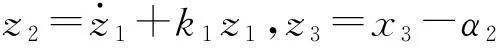
β(z3+α2-θ1x2-θ2Sf+d1)

(14)

设计虚拟控制量α2为

(15)

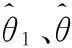
将式(15)代入式(14)，可得

(16)

φ1=β[x2Sf000]T

若设计α2s2满足如下镇定条件[3]：

(17)

式中，ε1为任意小的可设计参数，ε1>0。

则满足式(17)的α2s2设计如下：

(18)

式中，θM为参数的最大摄动量矩阵，θM=θmax-θmin；θmax、θmin分别表示各参数的估计上界矩阵和估计下界矩阵。

进一步有

(19)

(20)

进一步，最终控制器可设计为

(21)

us1=-k3z3

式中，k3为待设计的反馈增益，k3>0；ua为基于模型的补偿项；us1、us2为鲁棒项。

将式(21)代入式(19)，可得

(22)

若设计us2满足下式[3]：

(23)

式中，ε2为任意小的可设计参数，ε2>0。

则满足式(23)的us2为

(24)

h2≥‖θM‖‖φ2‖+|∂α2/∂x2|δ1+δ2

选取参数自适应律：

(25)

式中，Γ为可设计自适应增益矩阵，Γ=diag(Γ1，Γ2，…，Γ5)。

控制系统总体结构如图3所示。

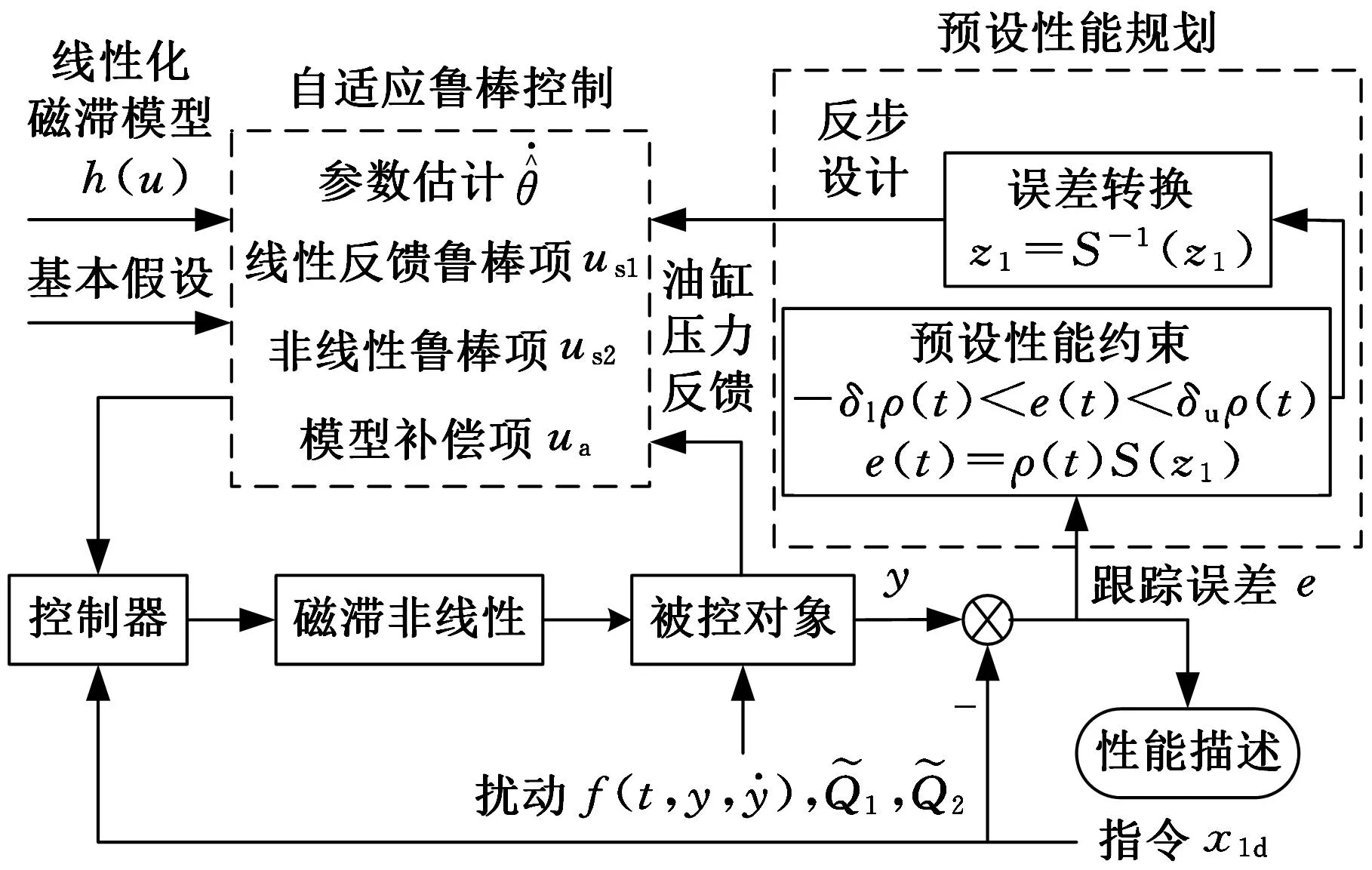
图3　控制系统总体框图

2.3稳定性证明

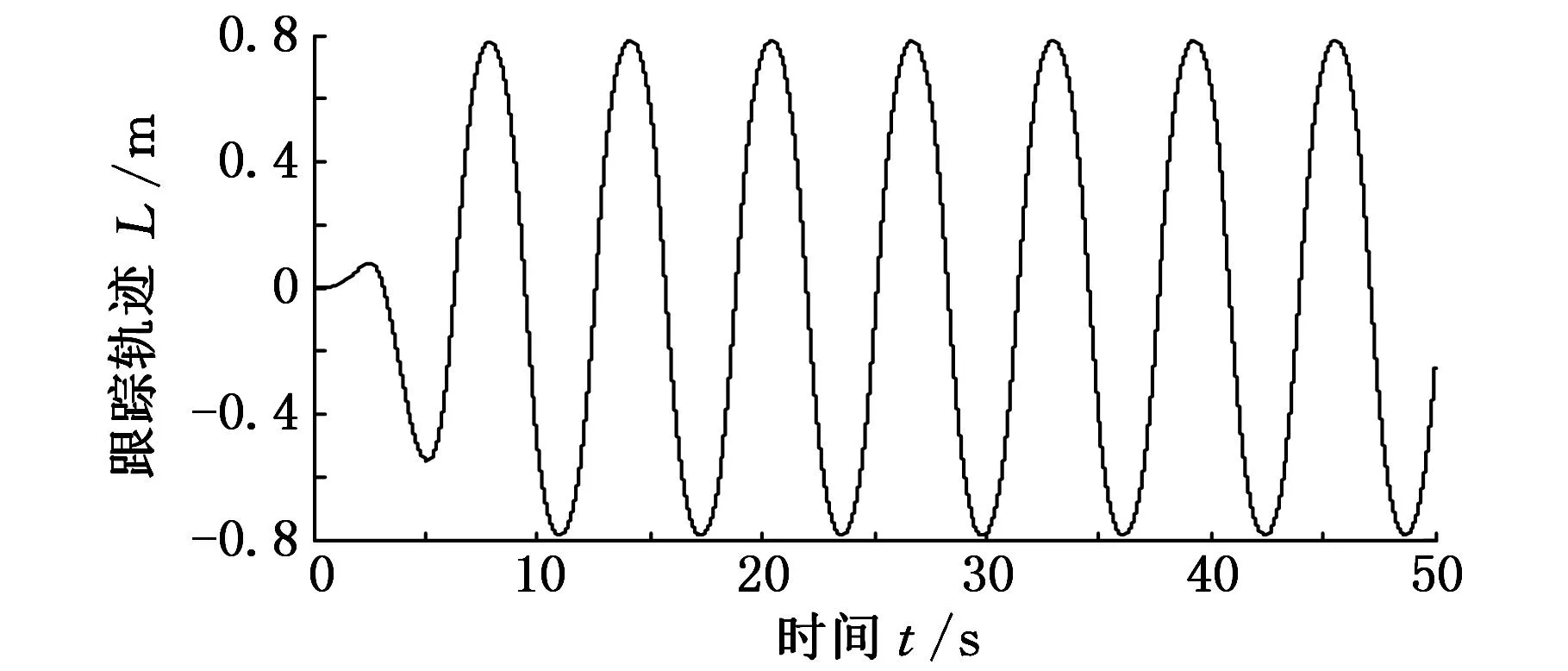
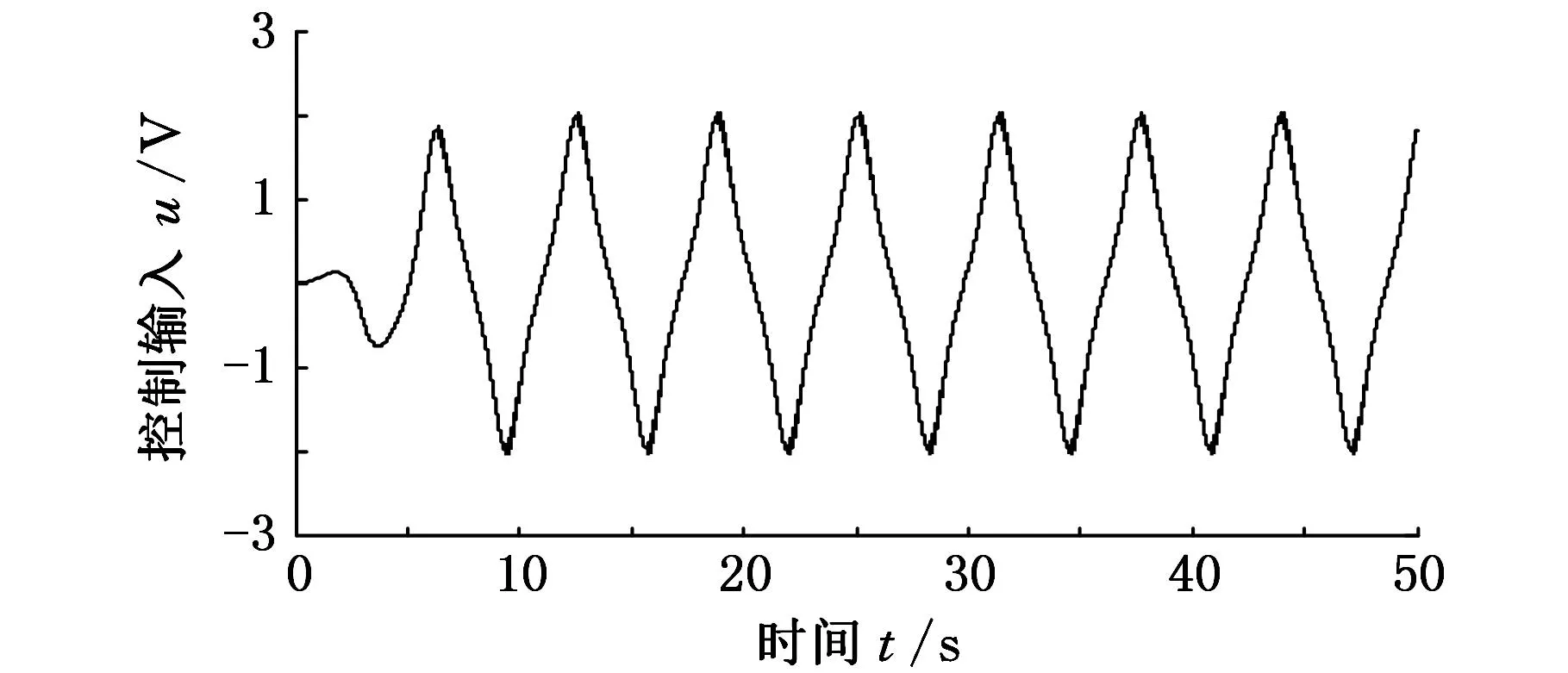
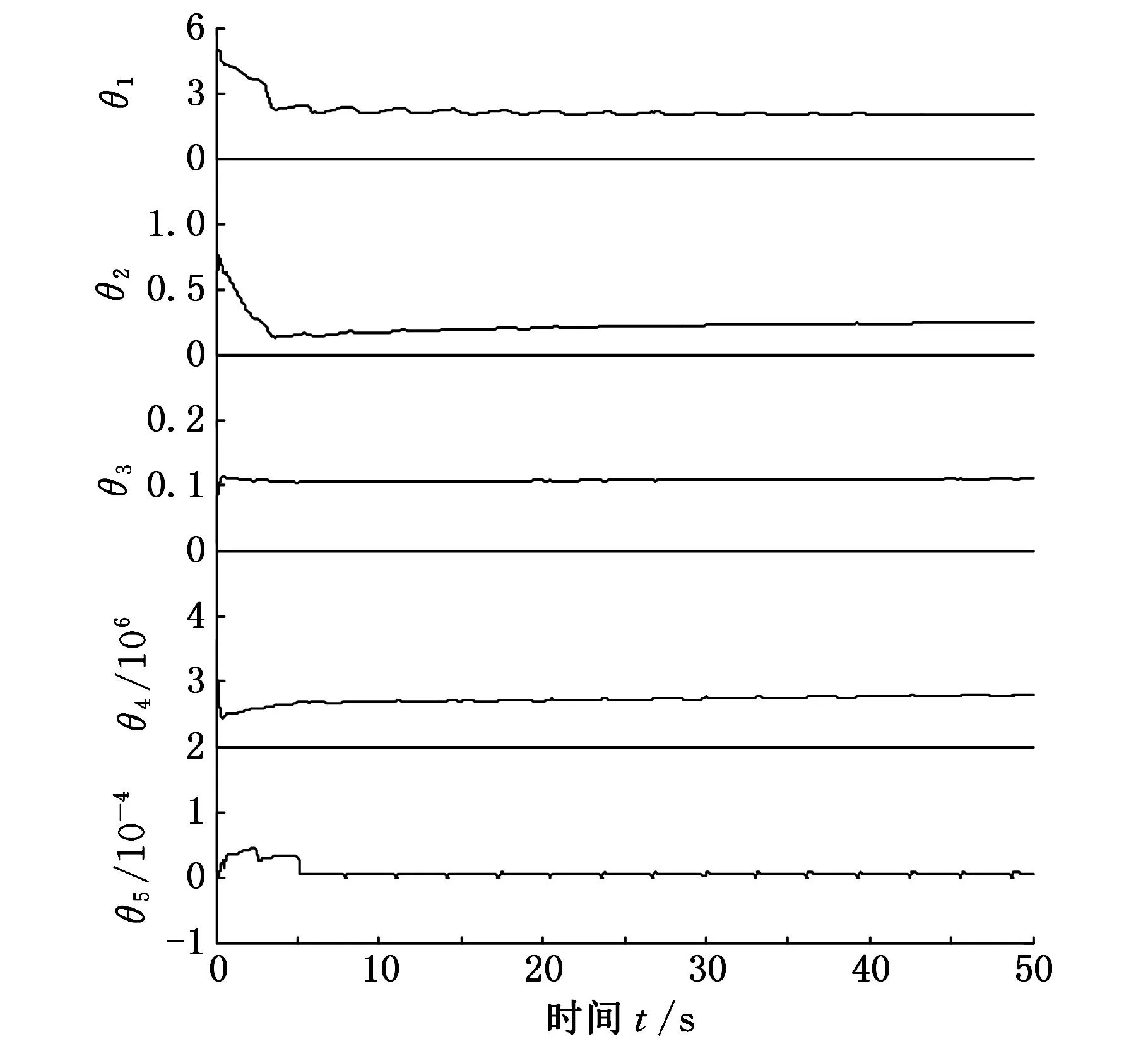
选取系统初始条件满足-δlρ(0)

选取Lyapunov函数：

(26)

对式(26)求导，并结合式(16)、式(22)，可得

(27)

Z=[z1z2]Tε=ε1+ε2

通过合理地选取参数k1、k2和k3，使得矩阵Λ为正定矩阵，若定义λmin(Λ)为矩阵Λ的最小特征值，则由式(27)可得：

(28)

由式(28)可知，通过合理地选取参数k1、k2和k3，控制器(式(21))可实现系统有界稳定，即转换跟踪误差z1有界；进一步由式(9)、式(10)可知，所设计控制器可保证跟踪误差e1有界，进一步通过调节ρ0、ρ∞、k、δl和δu等参数，可使得系统最终满足式(8)中所描述的预设性能。

3　仿真与分析

本文所研究阀控液压缸系统具体参数如表1所示。为了充分验证本文所设计控制器的有效性，在MATLAB/Simulink中搭建系统仿真模型，选取以下3个控制器进行对比仿真验证。

(1)自适应鲁棒控制(adaptiverobustcontrol，ARC)。该控制器使用广泛，其具体形式可参考文献[1]，参数k1=100，k2=150，k3=300。

(2)含磁滞补偿的预设性能自适应鲁棒控制(prescribedperformanceadaptiverobustcontrolwithhysteresiscompensation，PPARCH)，即为本文所设计控制方法，控制器各参数如下：k1=100，k2=50，k3=150，ρ0=0.3，ρ∞=0.001，k=0.5，δl=δu=10。自适应律(式(25))中的参数Γ=diag(40，2.5，0.02，1×1014，1×10-7)。

(3)不含磁滞补偿的预设性能自适应鲁棒控制(prescribed performance adaptive robust control，PPARC)，即在控制器设计过程中，忽略磁滞特性的模型补偿，而仿真时在系统模型中加入磁滞环节。各控制器参数选取同PPARCH。

表1　阀控单出杆液压缸位置伺服系统参数

系统参数估计的上下界矩阵分别为

θmin=[000.012×1060]T

θmax=[510.58×1060.0001]T

参数估计初值矩阵为

θ0=[000.012×1060.0001]T

系统外干扰d=0.5sin(2πt)，系统初始位置x1(0)=0.1 m，显然该初始位置满足初始条件要求-δlρ(0)

选取系统位置跟踪指令x1d=(1-exp(-0.01t2))arctan(sint)，如图4所示。

图4　位置跟踪指令

磁滞模型曲线见图1，系统仿真曲线如图5～图8所示。

图5　PPARCH作用下的控制输入

图6　初始段0～0.3 s跟踪误差对比

图7　稳态段20～50 s跟踪误差对比

图8　PPARCH参数估计

图5所示为PPARCH下的控制输入曲线，显然，受磁滞非线性的影响，控制输入在峰值处存在轻微的抖动，但控制输入整体光滑且始终有界。图6所示为初始段0～0.3s的跟踪误差。由于初始位置不匹配，因此在跟踪初始时刻，3个控制器的系统跟踪误差均较大，但都以较快速度收敛，其中，ARC出现了较大的超调，PPARC和PPARCH在预设性能函数的作用下，无明显超调，且跟踪误差收敛速度快于ARC。图7所示为稳态段(20～50s)的跟踪误差，ARC的跟踪误差较大，约为0.03mm，PPARC(约0.02mm)较ARC有了较大改善，PPARCH通过对磁滞的补偿作用，跟踪误差进一步减小，实现了最佳的跟踪精度(约0.01mm)。图8给出了系统各参数的估计曲线，由于初始位置不匹配，初始段各参数估计值出现了较大的突变，然而在自适应律的作用下，各曲线逐渐收敛并保持稳定。

4　结论

(1)将系统磁滞非线性模型简化为线性项和有界干扰项之和，可便于后续控制器的设计。

(2)通过设计预设性能函数，对系统跟踪误差的超调量、收敛速度、稳态精度等性能指标进行了合理了规划，并结合自适应鲁棒控制策略，设计了优良的预设性能控制器。

(3)通过与传统自适应鲁棒控制器的仿真对比，验证了预设性能函数对跟踪误差瞬态性能的改进作用；通过与不含磁滞补偿的预设性能控制器进行仿真对比，验证了所使用磁滞补偿策略的有效性。

[1]赵静一，程斐，郭锐，等. 自行式载重车悬架升降电液同步驱动控制研究[J]. 中国机械工程，2014，25(7)：972-978.

ZhaoJingyi,ChengFei,GuoRui,etal.ResearchonElectro-hydraulicSynchronizationDrivingControlforSelf-propelledTransporterSuspensionLifting[J].ChinaMechanicalEngineering, 2014, 25(7):972-978.

[2]YaoJianyong,JiaoZongxia,ShangYaoxing,etal.AdaptiveNonlinearOptimalCompensationControlforElectro-hydraulicLoadSimulator[J].ChineseJournalofAeronautics, 2010, 23(6): 720-733.

[3]YaoBin,BuFanping,ReedyJ,etal.AdaptiveRobustMotionControlofSingle-rodHydraulicActuators:TheoryandExperiments[J].IEEE/ASMETransactionsonMechatronics, 2000, 5(1): 79-91.

[4]唐锐，王少江，侯力，等. 并联机床伺服系统双自适应模糊滑膜控制[J]. 农业机械学报，2012，43(10)：229-234.

TangRui,WangShaojiang,HouLi,etal.DoubleAdaptiveFuzzySlidingModeControlforValveControlledAsymmetricCylinderSystem[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2012, 43(10):229-234.[5]ZhaoJiangbo,WangJunzheng,WangShoukun.FractionalOrderControltotheElectro-hydraulicSysteminInsulatorFatigueTestDevice[J].Mechatronics, 2013, 23(7): 828-839.[6]徐胜男，周祖德，艾青松，等. 基于粒子群优化的神经网络自适应控制算法[J]. 中国机械工程，2012，23(22)：2732-2738.

XuShengnan,ZhouZude,AiQingsong,etal.NeuralNetworkAdaptiveControlAlgorithmModifiedbyPSO[J].ChinaMechanicalEngineering, 2012, 23(22):2732-2738.

[7]RovithakisGA,BechlioulisCP.RobustAdaptiveControlofFeedbackLinearizableMIMONonlinearSystemswithPrescribedPerformance[J].IEEETransactiononAutomaticControl, 2008, 53(9): 2090-2099.

[8]BechlioulisCP,RovithakisGA.PrescribedPerformanceAdaptiveControlforMulti-inputMulti-outputAffineintheControlNonlinearSystems[J].IEEETransactiononAutomaticControl,2010, 55(5): 1120-1226.

[9]MerrittHE.HydraulicControlSystems[M].NewYork:Wiley, 1967.

[10]SuCY,StepanenkoY,SvovodaJ,etal.RobustAdaptiveControlofaClassofNonlinearSystemswithUnknownBacklash-likeHysteresis[J].IEEETransactiononAutomaticControl, 2000, 45(2): 2427-2432.

[11]ZhouJing,WenChangyun,ZhangYing.AdaptiveBacksteppingControlofaClassofUncertainNonlinearSystemswithUnknownBacklash-likeHysteresis[J].IEEETransactiononAutomaticControl, 2004, 49(10): 1751-1757.

[12]RudermanM,BertramT.ControlofMagneticShapeMemoryActuatorsUsingObserver-basedInverseHysteresisApproach[J].IEEETransactiononControlSystemsTechnology, 2014, 22(3): 1181-1189.

[13]YaoJianyong,JiaoZongxia,MaDawei.Extended-state-observer-basedOutputFeedbackNonlinearRobustControlofHydraulicSystemswithBackstepping[J].IEEETransactionsonIndustrialElectronics, 2014, 61(11): 6285-6293.

(编辑张洋)

Prescribed Performance Tracking Control of Electro-hydraulic Servo Systems with Hysteresis Compensation

Dong ZhenleMa DaweiYao JianyongWang Xiaofeng

Nanjing University of Science and Technology，Nanjing，210094

For the common parametric uncertainties and uncertain nonlinearities(hysteresis, nonlinear friction, external disturbances, et al) existing in electro-hydraulic servo systems, a novel method was proposed, which was based on adaptive robust control, and named prescribed performance tracking control with hysteresis compensation. First, taking valve controller single-rod hydraulic cylinder position servo system for instance, a mathematic model consisting of hysteresis nonlinearity was constructed. And then, a prescribed performance function was utilized to characterize the convergence rate, maximum over-shoot, and steady-state errors. At last, an adaptive robust controller was design based on the planned tracking errors to guarantee the excellent steady-state performance and transient performance. Extensive simulations show that the proposed controller can attenuate the hysteresis effects on the tracking accuracy, improve the convergence rate, reduce the over-shoot, and eventually achieve an excellent tracking.

electro-hydraulic servo system; hysteresis; prescribed performance control; modeling uncertainty; adaptive robust control

董振乐，男，1988年生。南京理工大学机械工程学院博士研究生。主要研究方向为机电液伺服系统非线性控制。发表论文3篇。马大为，男，1953年生。南京理工大学机械工程学院教授、博士研究生导师。姚建勇，男，1984年生。南京理工大学机械工程学院副研究员。王晓锋，男，1962年生。南京理工大学机械工程学院研究员、博士研究生导师。

2015-04-07

国家自然科学基金资助项目(51305203)；江苏省自然科学基金资助项目(BK20141402)

TP271.3

10.3969/j.issn.1004-132X.2016.08.001