2015年浙江省宁波卷第26题解法探究及反思

蔡卫兵（浙江省宁波市鄞州实验中学）

2015年浙江省宁波卷第26题解法探究及反思

蔡卫兵（浙江省宁波市鄞州实验中学）

2015年浙江省宁波市中考试题第26题由多个层次清晰、梯度分明的小题构成，侧重考查学生异中求同、由形悟质的能力，充分体现了知识与能力并重，思想与方法交融的命题特点.因此，在数学教学中，应开展一题多解、多解归一的训练，让学生在寻求不同途径和思维方式的过程中积淀出质的方法和思想，真正获得有价值的经历.

中考试题；相似模型；同而不同；积淀思想

让学生在实践中反思，在反思中体验，在体验中感悟，在感悟中提升，这应是数学教学的本真所在.细品2015年浙江省宁波市中考试题第26题，笔者深有感触.

一、试题呈现

题目如图1，在平面直角坐标系中，点M是第一象限内一点，过点M的直线分别交x轴，y轴的正半轴于A，B两点，且M是AB的中点．以OM为直径的⊙P分别交x轴，y轴于C，D两点，交直线AB于点E（位于点M右下方），连接DE交OM于点K．

图1

（1）若点M的坐标为M（3，4）.

①求A，B两点的坐标；

二、解法探究

1．基本套路是保证

从思维的角度分析，解题过程实际上是对思维活动的组织，最重要的是由题目的核心条件推断出哪些相关知识与结论，联想到哪些基本图形与途径，清楚地联系要求的最终结论.因此，解决数学问题，除了必须掌握有关数学内容的基础知识以外，还应多联想有用的解题思路和常用的解题方法.此题第（1）小题主要考查学生对已知条件的整合能力和观察识图能力.第①问由见直径找直角的基本思路连接DM，MC，由三角形中位线定理求得A，B两点的坐标.第②问要求ME的长，由ME=BE-BM可知，只要求出BE和BM的长即可，BM的长可由AB长的一半求得，而AB长可由勾股定理求得，求BE的长是解决此问的关键.从图形的直观角度，依靠寻找识别相似三角形基本图形的基本思路便可获得思维突破.

分解图形显相似解第（1）小题.

解：（1）①A（6，0），B（0，8）.

②（方法1）借助基本图形1（如图2）.

如图3，因为∠BOM=∠BED，且∠OBM=∠EBD，

所以△OBM∽△EBD.

由已知，得OB=8，BD=4，BM=5.

从而，得BE=6.4.

所以ME=1.4.

图2

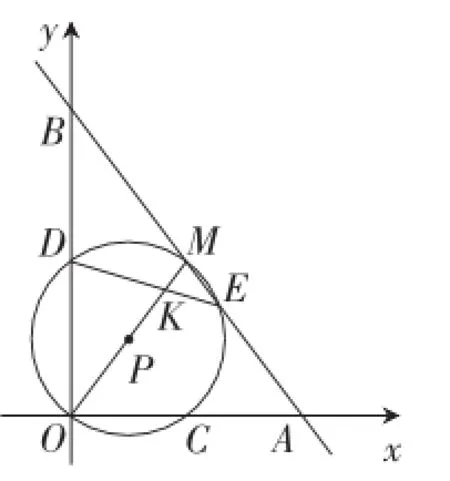
图3

（方法2）借助基本图形2（如图4）.

如图5，连接DM，OE.

因为OM为⊙P的直径，

所以∠ODM=∠OEM=90°.

所以∠BDM=∠OEB.

又因为∠DBM=∠EBO，

所以△DBM∽△EBO.

计算部分略.

图4

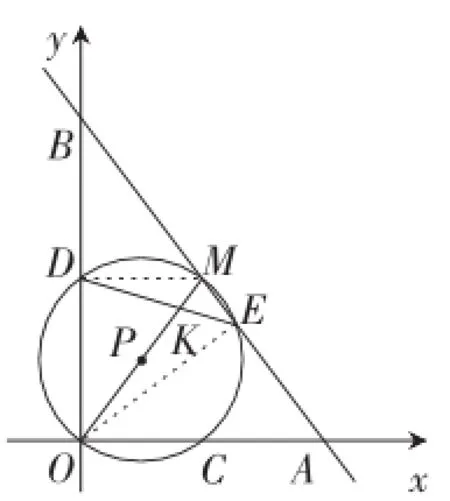
图5

（方法3）借助基本图形3（如图6）.

如图7，连接OE.

可得∠AOB=∠OEB=90°.

因为∠OBA=∠EBO，所以△OBA∽△EBO.计算部分略.

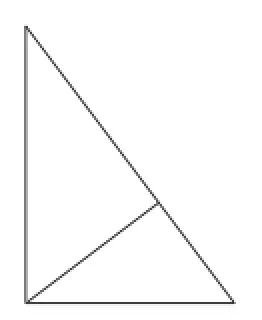
图6

图7

2．倍分关系寻相似

平行巧转化解第（2）小题.

（2）（方法1）如图8，连接DP.

由DP为△BOM的中位线，可知DP∥BM.

所以OM=4MK，PM=2MK，PK=MK.

因此可证得△DPK≌△EMK.

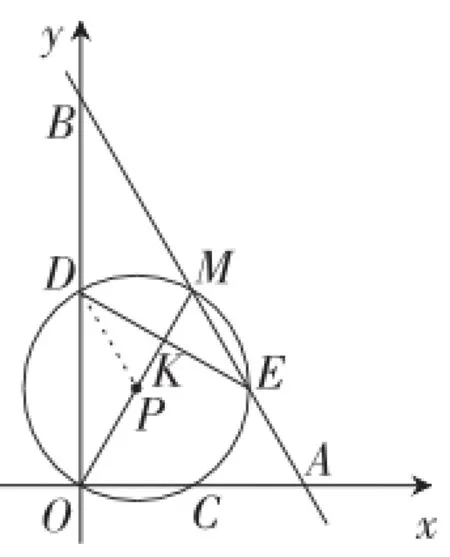
图8

所以DK=KE.

因为OM为直径，

所以OM⊥DE，

即∠DPK=60°.

（方法2）如图9，连接DM，OE，延长DE交x轴于点F.

图9

由于DM为△AOB的中位线，可知DM∥OA，且OA=2DM.

所以AF=DM.

因此可证△DME≌△FAE.

所以ME=AE.

因为OM为直径，所以∠OEM=90°.

所以OE垂直平分AM.所以OM=OA.

因为OM为Rt△AOB斜边上的中线，

所以OM=AM.

所以△AOM为等边三角形.

所以∠OAM=60°.

所以∠OBA=30°.

（方法3）如图10，过点O作OF∥AB，交ED的延长线于点F，连接OE.

由已知，得△BDE≌△O

图10

所以OF=BE.

由△OFK∽△MEK，

所以BE=3ME.

所以BM=2ME.

所以OM=2ME.

所以∠EMO=60°.

因为∠OBA+∠BOM=∠EMO，且∠OBA=∠BOM，

所以∠OBA=30°.

3．同而不同再类比

对比第（3）小题与第（2）小题，形式上互逆的关系和特殊到一般的关系，承接第（2）小题的思维过程的逆向方式，类比运用添平行寻相似实现线段倍分关系的转化思想方法.第（3）小题开放的是∠OBA的大小和点K的位置，用字母表示图中有关线段的长度或关系，体现出符号意识，通过代数式的运算进行数与式的变形是进行数学思考和表达的重要形式，类比迁移第（2）小题的解法可求出y关于x的函数解析式.

异中求同明思路解第（3）小题.

（3）（方法1）如图11，连接PD，DM，OE.

因为tan∠OBA=x，设BE=1，

则OE=BE·tan∠OBA=x.

设BM=OM=m，

所以ME=BE-BM=1-m.

所以在Rt△OEM中，

由ME2+OE2=OM2，得（1-m）2+x2=m2.

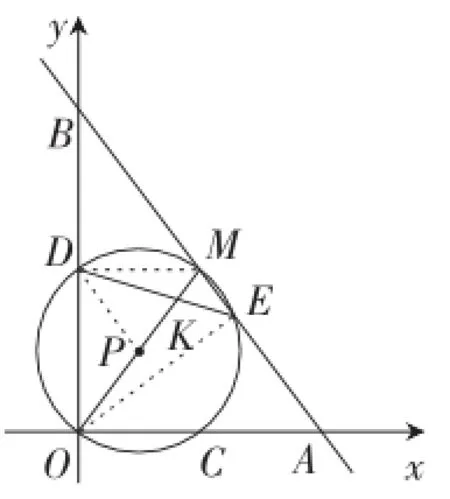
图11

因为△DPK∽△EMK，

（方法2）如图11，连接PD，DM，OE.

因为tan∠OBA=x，设BE=1，

由△BDM∽△BEO，

（方法4）如图12，连接DM，OE，延长DE交x轴于点F.

图12

因为tan∠OBA=x，设BD=1，

由△OAE∽△BAO，

由△DME∽△FAE，

由△FOK∽△DMK，

（方法5）如图13，过点O作OF∥AB，交ED的延长线于点F，连接OE.

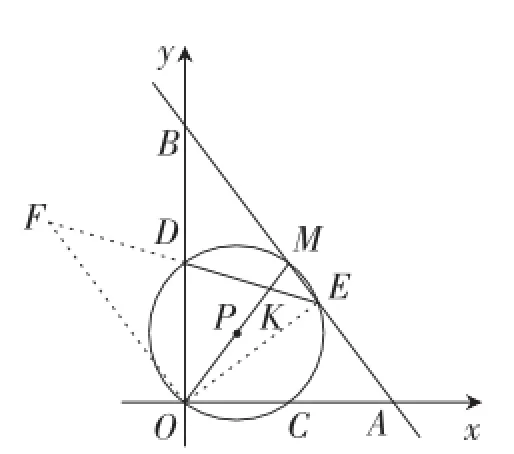
图13

三、解后反思

此题难度较大，巧妙地把圆放置于平面直角坐标系中，着重考查圆的基本性质、圆周角定理、平行线的性质、点的坐标、勾股定理、相似三角形的判定和性质、三角形中位线定理、全等三角形的判定和性质、锐角三角函数定义、特殊角的三角函数值、等腰三角形的性质，以及由实际问题列函数关系式和方程思想的应用，将重要的数学知识点和数学思维体现得淋漓尽致.第（1）小题第①问门槛低，有利于学生解决，第②问有效地设置台阶，为后续的探究做好铺垫.第（2）小题需要学生对所学知识融会贯通、灵活运用.第（3）小题类比运用前面所获得的思想方法，同时渗透了用代数方法解决几何问题的思维方式，更重视代数分析能力和计算能力，有一点初、高中衔接的味道.三道小题层次感强，既有直接要求计算、求解的问题，又有以尝试、猜测、探究形成设问的问题，体现了压轴题的选拔功能，这也将成为教师日常教学的导航，也是中考复习的一个风向标.

1.直击关键，建构方法体系

在解中考数学压轴题时，既要对已知的条件进行全面分析，还要善于将题目中的隐性条件挖掘出来，将数学中各知识点之间的联系巧妙地运用起来，用全面、全新的视角来解决问题.熟悉和掌握一系列基本图形及其相关结论，将一些重要的基本方法了然于胸，自然会在具体问题中通过对题目核心条件与结论的分析捕捉题目的特点，并能将其特点转化为有效的解题方法，这是探索方向的保证.上述各道小题的多种解法殊途同归，精彩纷呈，其关键是善于发现并提取基本模型，陌生问题熟悉化；善于联想并运用基本方法，复杂问题简洁化；善于比较并联系前后异同，异中求同类比化.在解决问题时，要注意从数量和图形两方面寻求突破，多归纳总结解题方法，多积累诸如此题中“倍分关系寻相似，添线平行成习惯，构造A型图或X型图实现线段代换少麻烦”的解题经验，建构解决问题的方法体系.

2.关注本质，积淀思想方法

试题先由点M（3，4）为定点起步，感知并辨认出基本图形，寻找与此题的关联点实现转化，然后变为线段OM上的定比分点k，需要添加辅助线构造出相似三角形，以及实现线段倍分关系的转化，最后开放的是∠OBA的大小随着动直线AB的变化而变化，在此过程中探究点K的位置的变化规律而寻找线段比值之间的函数关系，有数与式的转化，较好地体现了符号意识.问题逐步深入，遵循了由特殊到一般的思想，追求逻辑连贯，其解法始终有一条主线（相似基本模型助突破）贯穿其中，这就是问题积淀的质，在解法中融入典型的数学思想，即模型思想、转化思想、数形结合思想、类比思想.解题探究重在培养思维能力，读懂条件的每一个信息，联想基本图形，寻找到解题的多种策略以及方法的核心本质，在做的过程和思考的过程中积淀思想，久而久之，便形成可持续发展的数学解题技巧和数学解题能力.

［1］徐秀峰.数形巧突破转化妙解题［J］.中学数学教学参考（中旬），2015（5）：31-32.

［2］刘家良.由形到质异中求同积淀思想：2014年天津市中考第25题评析及教学导向［J］.中国数学教育（初中版），2015（4）：58-60.

蔡卫兵（1976—），男，中学高级教师，主要从事初中数学教育与解题教学研究．

2016—02—13