“切线长定理”教学设计
2016-08-13黄丽萍四川省宜宾市南溪一中外国语实验学校
黄丽萍(四川省宜宾市南溪一中外国语实验学校)
“切线长定理”教学设计
黄丽萍(四川省宜宾市南溪一中外国语实验学校)
对切线长定理的探究及证明过程设置为四个活动,通过“观察—猜想—验证—证明—应用”,总结出研究“切线长定理”这类数学问题的方法,在这个过程中激发学生思维,培养学生的合作精神,渗透从特殊到一般的数学思想,培养学生的形象思维和抽象思维能力.
自主探究;合作交流;应用拓展
教学内容解析
1.教材内容
“切线长定理”是华东师大版《义务教育教科书·数学》九年级下册第二十七章“圆”的第二节的内容,主要学习切线长定理及其简单应用,着重研究切线长定理的证明.
2.教学重点
切线长定理.
3.地位作用
本节课的内容是切线长定理,它是在学生学习了切线的定义、判定和性质的基础上,继续对切线的性质的研究,是直线与圆位置关系的重点内容,也是继垂径定理之后对圆的对称性再一次的认识.体现了图形的认识、图形的变换、图形的证明的有机结合,既是前面知识的延伸,又是后面学习的基础,更是今后证明线段相等、角相等、弧相等、线段成比例等的重要工具.
教学目标
(1)理解切线长定义,掌握切线长定理,并能初步运用;
(2)引导学生经历观察、猜想、验证、证明、应用活动,培养学生的合作交流意识和创新意识,提高数学建模能力,训练发散思维;
(3)通过对切线长定理的猜想和证明,培养学生严谨的思维能力和严密的演绎推理能力.
教学问题诊断分析
1.学生学情分析
(1)知识基础.
学生已具备轴对称、勾股定理、相似三角形、圆的对称性、切线的判定与性质等知识基础.
(2)活动经验.
学生具有一定的动手操作、自主探究、合作学习的经验.
(3)能力特点.
学生具有初步的演绎推理能力,但证明命题的能力尚未完全形成.
2.教学难点
切线长定理的探究并证明.
3.突破难点的策略
通过情境创设,激发兴趣.设置层层深入的问题,用巧妙的语言调动学生积极思考,采用不断追问的方式,逐步引向深入,培养学生严密的思维习惯.鼓励学生动手操作,合作交流,经历探索过程,得出结论.通过归纳小结和方法提炼环节,让学生内化本节课的知识和方法,从而突破难点.
教学策略分析
1.教材处理
(1)将本节内容细分为两课时.
教材把切线长定理及三角形内切圆合为一课时,探究内容和问题设计稍显单薄.为了丰富教学内容,体现深入探索切线长定理的重要性,在教学设计时将其分为两个课时,本节课是第一课时,只研究切线长定理的探索证明过程.
(2)保留教材探究,改编课后练习.
教学设计中保留了教材中“根据实例,由特殊到一般,运用动态的变换方法,通过合情推理,发现图形的性质,然后通过演绎推理证明这一性质”的探究内容,为了加深对切线长定理的理解,使学生学会发现、分析、解决问题,培养学生正确应用所学知识的能力,笔者还对教材课后练习进行了挖掘,将教材习题进行改编,放在切线长定理的证明之后,作为对新知识的简单应用.
(3)补充拓展延伸.
由于笔者所教班级的学生数学基础较扎实,接受新知的能力较强,因此补充了拓展延伸,提出开放性问题,对图形进一步剖析,从而让学生品尝发现结论所带来的快乐,满足学生的学习需求,培养学生思维的完整性和深刻性.
2.教学方法
根据本节课的教学目标、教材内容以及九年级学生已基本形成的逻辑推理的思维能力,若利用形象直观的教具和生动的几何画板软件,则可以辅助学生抽象思维的进一步形成,所以教学时采用直观演示实验以及猜想论证法,然后加以引导、启发学生,让学生经历观察、画图、猜想、论证,以及讨论、分析、演示相结合的教学过程,意在帮助学生通过自己动手试验、分析归纳,从自己的实践中获取知识,并通过讨论来加深对知识的理解.
3.学习方法
新课改的精神在于以学生的发展为本,把学习的主动权还给学生,倡导积极主动、勇于探索的学习方法.因此,本节课主要采取动手实践、自主探索与合作交流的学习方式,通过让学生猜想、论证、应用,建构起自己的知识结构,使学生成为学习的主人.
4.教具准备
教材、多媒体课件、实物投影仪、圆规、三角板等.充分利用现代信息技术,使学生通过形象直观的感觉,加深对知识的理性认识.
教学过程
1.创设情境,引入新课
欣赏生活中的图片,并提出问题.
问题1:在如图1所示的照片中有哪些几何图形?

图1
学生活动:学生欣赏图片,思考、反馈,体会生活中的几何图形,并大胆说出自己的看法.
【设计意图】从生活中的实例引入新课,激发学生的学习兴趣,唤起他们的好奇心与求知欲,同时对过圆外一点可以画圆的两条切线形成初步的感性认识.
2.合作学习,探究新知
活动1:画一画.
问题2:在如图2所示的圆外任找一点P,并画出⊙O的两条切线?
学生活动:学生借助三角板,应用切线的判定画出切线.

图2
师:在实际应用中,我们根据需要,经常求点P与切点间的距离,因此,需要给出一个定义.
学生活动:学生独立思考,感知概念,充分理解切线长定义,正确区分切线和切线长.
(1)切线长.
①定义:圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.
②切线与切线长的区别.
切线是一条与圆相切的直线,不能度量;切线长是线段的长,可以度量.
【设计意图】从生活中的实例引入新课,激发学生的学习兴趣,唤起他们的好奇心与求知欲,同时对过圆外一点可以画圆的两条切线形成初步的感性认识.
活动2:折一折.

图3
问题3:若将图3所示的图形沿直线OP翻折,你能发现什么结论?
猜想:PA______PB,
∠APO______∠BPO.
问题4:过圆外任意一点画圆的两条切线都有这样的结论吗?
教师活动:利用几何画板软件分别变动圆外点P的位置及圆的大小,让学生观察线段PA与PB,∠APO与∠BPO是否相等?验证发现的结论,并引导学生归纳结论.
学生活动:学生通过动手翻折,以及利用几何画板软件展示,观察PA与PB,∠APO与∠BPO的大小关系,对线段长度、角度大小等问题进行多角度观察思考,寻找不同的解决问题的方法.全班互动交流,展示探究成果.
【设计意图】学生通过翻折、观察PA与PB,∠APO与∠BPO之间的关系,进而发现、猜想切线长定理,并用自己的语言表达出来,发挥学生的主体作用.几何画板软件的使用让静止的图形运动起来,使问题变得更加生动形象.这样的设计渗透了从特殊到一般的数学思想,培养学生的形象思维和抽象思维能力.
问题5:试用文字语言叙述刚才的结论?
学生活动:通过观察、猜想,同桌相互交流,归纳出结论.
(2)切线长定理.
定义:过圆外一点所画的圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角.
学生活动:学生指出切线长定理的题设和结论.
剖析定理:①指出定理的题设和结论;②结合图形,用符号语言表示定理,即如图4,若PA,PB分别与⊙O相切于点A,B,则PA=PB,∠APO= ∠BPO.

图4
【设计意图】此环节让学生熟练掌握定理的三种数学语言(文字语言、符号语言、图形语言)的表示以及相互转化.
活动3:证一证.
问题6:试证明你所发现的结论.
教师活动:切线长定理证明的教学方式采用学生自主探索与合作交流相结合,首先采取多种方式进行探索,等学生猜想出结论后,再明确告知学生,仅凭照片观察、折叠展示、动态演示,并不足以说明结论的严谨性,还需通过演绎推理证明结论.因此,要启发学生寻找证明的方法.
问题7:证明命题的步骤有哪些?
学生活动:学生独立思考,写出证明过程,再投影其过程.
第一步:分清命题的题设、结论;第二步:画图;
第三步:结合图形,写出已知、求证.
已知:如图5,PA,PB是⊙O的两条切线,切点分别为点A,B.
求证:PA=PB,∠OPA= ∠OPB.

图5
第四步:写出证明过程.
【设计意图】让学生在探究的过程中体验数学活动充满着探索性和创造性,感受证明的必要性,证明过程的严谨性.《义务教育数学课程标准(2011年版)》(以下简称《标准(2011年版)》)中对学生的推理能力的要求既有合情推理,又有演绎推理.在直观感知、操作确认的基础上,努力提高学生的直觉能力和合情推理、数学说理能力.《标准(2011年版)》的意图是大力培养合情推理的基础上发展学生的演绎推理能力.对学生来说,不仅要掌握证明的基本方法,同时也要理解证明的必要性,即证明在数学中的重要意义.
3.应用拓展,体验成功
已知:如图6,AC是⊙O的直径,PA,PB是⊙O的两条切线,切点分别为点A,B.求:

图6
(1)若OP=10,⊙O的半径为6,则PA=_____,PB=______.
(2)若OA=4,OP=8,则∠APO=_________,∠APB=________,∠CAB=________.
学生活动:第(1)小题由学生独立思考,回答问题,第(2)小题由同桌交流,展示方法.
【设计意图】此题让学生学会运用切线长定理来解决线段、角的问题,加深对切线长定理的理解,使学生学会发现、分析、解决问题,培养学生正确应用所学知识的能力.
问题8:在图6中连接AB,不难发现∠APO= ∠CAB,这个结论是否具有一般性?
学生活动:学生在问题的引导下进行深入思考,探究拓展.
【设计意图】问题8通过看似巧合的两角相等,把研究的对象从特殊引向一般,引导学生把握其内在规律,激发学生的探究欲望.
活动4:探一探.
拓展延伸:如图7,P是圆外一点,PA,PB是圆的两条切线,A,B是切点,我们知道AP= BP,∠APO=∠BPO.

图7
学生活动:学生动手操作,小组合作交流,感知多种结论,相互补充完善结论,优化列举,最后展示其成果,并说明理由.
问题9:若添加辅助线,你还可以推出哪些结论?
(1)____________________________;
(2)____________________________;
(3)____________________________;
(4)____________________________;
(5)____________________________.
学生活动:学生通过添加辅助线,小组合作,共同探究发现OP垂直平分弦AB,进而得到弧相等、弦相等、角相等、三角形全等、三角形相似等结论.
【设计意图】此处教师提出开放性问题,不仅能有效地提高学生的学习热情,培养学生自主学习的能力,还有利于培养学生的合作能力和创新精神.为以后解决相关的几何问题提供了思路.
在本节教学中,笔者注意突出定理的探究过程,重视学生主体地位的落实,让学生通过自主学习,合作探究,经历观察、猜想、验证、证明、应用等基本数学活动,探索切线长定理,从而品尝了发现结论所带来的快乐,培养学生思维的完整性和深刻性.
4.梳理小结,盘点收获
课堂小结时,让学生畅所欲言,谈谈这节课的收获是什么.教师进行补充、总结,为下节课做好铺垫.
学生活动:学生从数学知识、思想方法等方面进行全面总结.
教师引导学生总结:
(1)知识价值:切线长定理.
(2)模型化思想:证明命题的基本步骤及数学建模能力(基本图形).
(3)数学思维及思想方法:从具体到抽象,从直观、合情推理到严密逻辑推理的思维过程,使学生体会数学发展的过程及数形结合的数学思想,从特殊到一般、分类与整合等.
【设计意图】通过小结为学生创造交流的空间,引导学生参与总结,调动学生的积极性,反思自己的学习过程,让学生形成知识网络,完善认知结构.培养学生归纳、概括的能力,使本节课的知识得到梳理,学生的潜能得到挖掘.
5.推荐作业,巩固拓展
(1)必做题:教材第55页的练习1,2,3题.(2)选做题:思考题.
如图8,PA,PB是⊙O的切线,切点为点A,B.求AC 与OC,CP有何数量关系?

图8
学生活动:学生课后完成必做题,选择完成选做题.
【设计意图】在作业布置上分两部分,即必做题及选做题,让不同层次的学生都能得到发展.
最后,教师带领学生再次欣赏如图1所示的照片.
【设计意图】首尾呼应,体现数学来源于生活,最后应用于生活.
设计说明
1.设计理念
(1)采用“观察—猜想—验证—证明—应用”五步教学法的形式研究这类有规律性的数学问题,达成教学目标,也充分体现新课程的教学理念.
(2)注重数学思想方法的渗透,探究过程中学生经历由特殊到一般,模型化思想,提高学生的建模能力,进而培养学生严密的演绎推理能力.
(3)小组评价表(略)的作用:激励学习兴趣,同时对教学过程进行一个客观、理性的反思.
2.教学反思
(1)目标达成(目标检测).
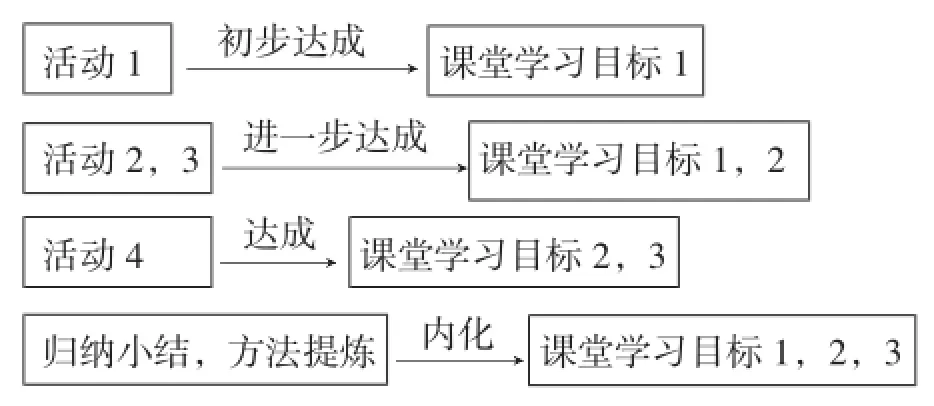
初步达成进一步达成达成活动1 课堂学习目标1活动2,3 课堂学习目标1,2活动4 课堂学习目标2,3归纳小结,方法提炼 课堂学习目标1,2,3内化
(2)课堂评价.
在教师评价时,关注学生的参与程度和思维水平,关注学生对基础知识的掌握情况和解决实际问题的意识和能力;其次,在教学过程中尊重学生的个体差异,对于学生的不同思维方式,只要合理都给予鼓励和肯定,帮助学生树立学习数学的自信心,充分发挥学生评价表,培养学生集体荣誉感.同时为学生提供生生评价的平台,让学生间学会质疑,学会相互欣赏、学习和借鉴.
(3)课后反思.
在整节课中,学生对教师创设的问题很感兴趣,他们积极思考、主动探究,踊跃回答问题.通过分组讨论、上台展示、师生交流、生生交流使思维碰撞出火花,生成了一些新的思路.学生的表现超出了笔者的预期,整节课在轻松愉悦的环境下达到学习目标.
在活动4中,笔者抛出开放性问题后,学生通过自主探究,小组交流,发现了很多有用的结论,全班同学积极发言,都迫切希望上台展示,但是由于时间关系以及本节课重点是探究、证明切线长定理,因此没能够让学生充分展示自己的结论.使得得出成比例线段、有关面积结论问题的学生较少,若能再给学生一些独立思考和交流的时间,相信效果会更好.
[1]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准(2011年版)》解读[M].北京:北京师范大学出版社,2012.
[3]朴昌虎,杜乙霞.有效教学的灵魂是以生为本:切线长定理教学案例与分析[J].延边教育学院学报,2011(2):52-55,58.
[4]刘金英,何志平,贯忠喜.2012年中考数学试题分类解析:空间与图形[J].中国数学教育(初中版),2013(1/2):54-69.
[5]章建跃.中学数学课改的十个论题[J].中学数学教学参考,2010(3):2-5.
黄丽萍(1989—),女,中学二级教师,主要从事中学数学教育教学研究.
2015—11—26
