比对新旧教材 体悟课程理念

韩新正（江苏省泰州市苏陈中学）

比对新旧教材体悟课程理念

韩新正（江苏省泰州市苏陈中学）

《义务教育数学课程标准（2011年版）》指出：在数学教学活动中，教师要把基本理念转化为自己的教学行为.新、旧教材在章节编排顺序、数学情境、具体内容等方面产生了不少变化.通过比对新、旧教材，管窥编者对课程的理解，并将这些变化体现在教学之中，让学生享受到教材调整带来的学习便利.

教学本质；情境创设；核心概念

苏科版《义务教育课程标准实验教科书·数学》（以下统称“苏科版《实验教科书》”）经过十多年的实验，在广泛听取专家、实验区师生的意见和建议的基础上，编写组对其进行了认真修订，经教育部2012年审定，从2013年起正式使用苏科版《义务教育教科书·数学》（以下统称“苏科版《教科书》”）.新、旧教材在章节编排顺序、数学情境、具体内容等方面都产生了变化.通过比对新、旧教材，我们从中管窥编者对课程的理解，并将这些变化体现在教学之中，不断提高教学效果.下面，笔者结合“一元一次不等式”一章中的“一元一次不等式组”一节内容予以说明，供参考.

一、新、旧教材的变化

1.在教材体系中位置的变化

“一元一次不等式组”是“一元一次不等式”一章的重要内容，苏科版《实验教科书》将其安排在八年级下册，是在代数式、整式的运算、一元一次方程、二元一次方程组、一次函数之后开始研究不等式；苏科版《教科书》将其安排在七年级下册的代数式、整式的运算、一元一次方程、二元一次方程组之后.这里主要出现了两点差异：第一是学习时间差异，两套教材安排的时间相差一年，后者比前者提前了整整一年；第二是苏科版《实验教科书》把其安排在一次函数之后，苏科版《教科书》把其安排在二元一次方程组之后.分析这一变化，可以感受到苏科版《实验教科书》把一次函数看成是二元一次方程的自然生长，比如二元一次方程x-y=2，只要移项就变成一次函数y=x-2，其间用一年的时间来体悟这种变化.其实，方程和函数是两种完全不同的思想，这样的安排顺序比较勉强.二元一次方程描述的是数量之间的等量关系，而一次函数是描述变化过程中两个变量之间的对应关系，两者是从不同的生活现实中抽象出来的数学模型，虽然方程和函数的解析式可以相互变形，并在坐标系中实现几何意义的理解，但其产生的背景不同.苏科版《教科书》把不等式安排在二元一次方程之后比较合理，在讲完列代数式、一元一次方程和二元一次方程组之后，学生的思维自然会提出这样的疑问：生活中存在数量之间的等量关系，是否存在不等关系呢？比如数字大小、速度快慢、人口多少等.另外，从学生知识建构的角度来看，当学生完成方程的知识建构后，他的知识网络中必然延伸出另一个分支——不等式，他的知识网络迫切需要补全不等式知识，知识体系方能全面，所以苏科版《教科书》的安排更加合理，是靠近学生最近发展区的安排，是符合学生认知规律的安排，也是学生自主建构的需要.

2.创设的情境不同

苏科版《实验教科书》创设的情境如下：某种杜鹃花适宜生长在平均气温为17～20°C的山区，已知这一地区海拔每上升100米，气温下降0.6°C，现测出山脚下的平均气温是23°C，估计适宜种植这种杜鹃花的山坡的高度.

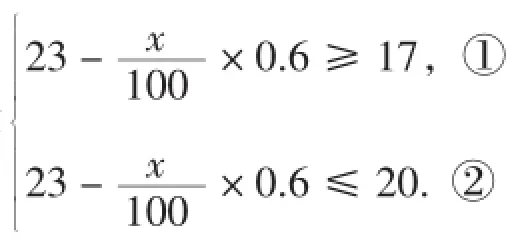
像这样，由几个含有同一个未知数的一次不等式组成的不等式组叫做一元一次不等式组.

苏科版《教科书》创设的情境如下：小丽早晨7时30分骑自行车上学，要在7时50分至7时55分之间到达离家3400 m的学校，小丽骑自行车的速度应在什么范围？

像这样，把几个含有同一个未知数的一次不等式联立在一起，就组成了一个一元一次不等式组.

苏科版《实验教科书》和苏科版《教科书》都是通过创设现实生活的情境列出两个不等式，然后得出不等式组的概念.但苏科版《实验教科书》创设的情境学生很难理解，为什么随着海拔的上升，气温会下降？（这是生活经验和地理知识造成的理解障碍）；另外，准确列出气温与海拔高度x的关系不是一件容易的事，如果没有教师的指导，很多学生是无法列出这样的不等式的.创设情境的目的旨在导入新课，让学生在非常愉悦的心境下进入新知识的学习和探究，相对于一节课的内容来讲，它是序曲、铺垫.如果学生在情境上花费太多的时间，甚至花了时间都列不出式子，教师还怎么导入新课？苏科版《教科书》创设的情境是大家都熟悉的生活现实，学生不存在理解上的障碍，容易列出不等式，且所列出的不等式简洁，为后面探求不等式组的解集提供了很大的方便.

3.教学的侧重点不同

苏科版《实验教科书》探求不等式组的解集过程如下.

（1）探求不等式组的解集.

先分别求出前面不等式组中两个不等式的解集：解不等式①，得x≤1000.解不等式②，得x≥500.显然同时满足不等式①②的未知数x应是这两个不等式解集的公共部分，在数轴上表示这两个不等式的解集，如图1所示.

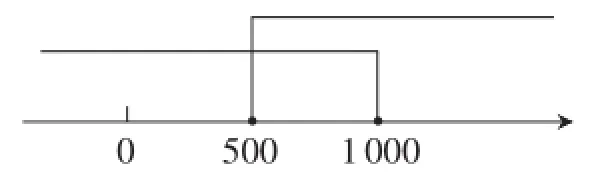
图1

这两个不等式的公共部分是500≤x≤1 000.然后给出不等式组的解集和解不等式组的定义.

（2）例题.

具体解法略.

（3）练习题.

解下列不等式组：

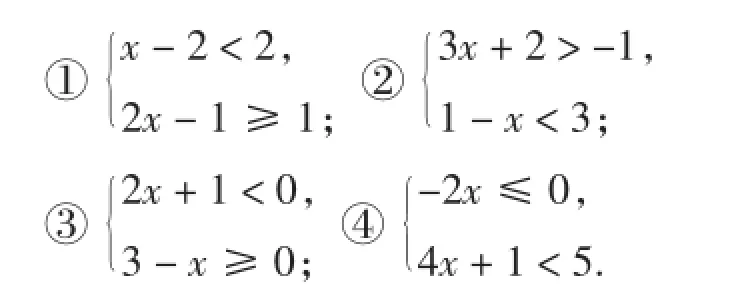
苏科版《教科书》探求不等式组的解集过程如下.

（1）探求不等式组的解集.

这一过程基本和苏科版《实验教科书》相同（略），但例题、练习题的设计不同.

（2）例题.

具体解法略.

（3）练习题.

①根据数轴上表示的不等式组中两个不等式的解集，写出不等式组的解集，如图2、图3所示.

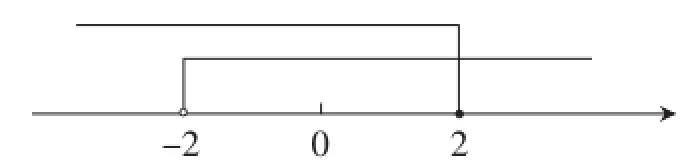
图2

图3

②利用数轴确定下列不等式组的解集.

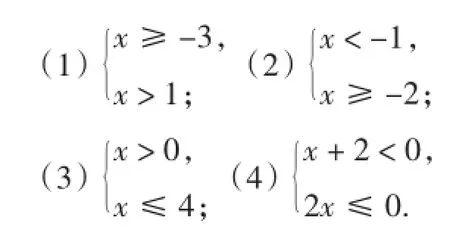
苏科版《实验教科书》和苏科版《教科书》在探求不等式组的解集中采用的方法相同，都是先求出两个不等式的解集，然后再把每个不等式的解集表示在数轴上，找出其公共部分，得出不等式组的解集.再用例题巩固求不等式组的解集的方法.这里出现了两点变化，首先，由于创设的情境不同，苏科版《实验教科书》中学生把很多时间花在解不等式上（因为不等式较繁），难以迅速进入教学的重点（求不等式组的解集）；后者情境简洁，所列不等式组简单，学生口算就能得出结果，比较轻松地求出不等式组的解集.其次，例题、练习题部分设计不同，苏科版《实验教科书》是相对复杂一点的不等式组，使用的是解不等式组，学生首先要解出不等式的解集，然后利用数轴求不等式组的解集；而苏科版《教科书》的例题、练习题是直接给出最简单的不等式组，使用的是利用数轴确定不等式组的解集，学生直接运用数轴求解即可，设计目的明确，就是突出对不等式组的解集这一重、难点的突破.因为前面已经学习了解不等式，后面还将继续学习解不等式组，所以本节课的重点不是解不等式（组）.设计突出重点，不拖泥带水.理解了这一点，就更有利于理解教学.

二、在新、旧教材比对中理解课程理念

只有深刻理解课程标准，并在课标精神引领下的课堂才能充满生机和活力.为此，教师要理解学生、理解教学、理解教材.教材是课程的体现，是教学的素材.通过比对新、旧教材，从教材的新、旧变化中，管窥编者对课程的理解，进而将这些理解落实到教学中，不断优化我们的课堂，让课堂教学更高效.

1.课堂教学从适切的情境开始

高效的课堂教学必须从适切的情境开始.《义务教育数学课程标准（2011年版）》（以下简称《标准（2011年版）》）在第四部分实施建议中指出，数学教学应根据具体的教学内容，注意使学生在获得间接经验的同时也能够有机会获得直接经验，即从学生实际出发，创设有助于学生自主学习的问题情境.《标准（2011年版）》同时在教材编写建议中指出，呈现内容的素材应贴近学生现实.只有贴近学生实际的现实（包括生活现实、数学现实、其他学科现实），才能激发学生的学习兴趣，自然导入新课，引领学生进入新知的探求过程中.课堂教学从适切的情境开始，学生在熟悉的氛围中发现问题、提出问题，并在最近发展区获得最大收获.苏科版《实验教科书》的情境对多数学生来说比较陌生，学生难以列出不等式（组），列出的不等式（组）比较烦琐，这对通过创设情境进入新知探求，是一个很大的障碍，必然会分散学生的精力，影响新知的学习.针对这一情况，苏科版《教科书》及时做了修改，所创设的情境对所有学生来说都很熟悉，且列出的不等式（组）简洁，学生口算也能解答，在熟悉的情境中自然进入不等式组的解集的探求之中，整个环节自然流畅，知识自然生长.所以，高效的课堂教学必须从适切的情境开始.

2.课堂教学要沿着“核心概念”这根主线展开

《标准（2011年版）》在教材编写建议部分指出，教材编写应当体现整体性，注重突出核心内容，注重内容之间的相互联系，注重体现学生学习的整体性.联系到课堂教学就要围绕核心概念展开.从情境创设到重、难点突破，从例题安排到练习训练，从师生活动到板书设计等，我们都要围绕“核心概念”展开，并始终将其作为教学的主线.本节课的重点是利用数轴探求不等式组的解集，在探求解集的过程中理解数形结合思想，掌握不等式组的解集的求法.但苏科版《实验教科书》从情境、例题、练习的设计中，更多关注的是不等式组的解法，其实不等式的解法前面已经学过，不等式组的解法下一节课会详细学习，从这一角度思考，苏科版《实验教科书》对本节课的设计需要改进.苏科版《教科书》认准本节课的核心概念是不等式组的解集，本节课从小丽骑车这一大家都熟悉的情境开始，先列出简单的不等式组，然后提出怎样求它的解集，接着引导学生在数轴上求两个不等式的公共部分，所设例题和练习题也是求不等式组的解集，而不是解不等式组，全篇围绕不等式组的解集这一核心概念展开教学，主线明确，故而高效.

3.在新、旧教材比对中理解课堂教学

《标准（2011年版）》指出，在数学教学活动中，教师要把基本理念转化为自己的教学行为.随着《标准（2011年版）》 的颁布，课堂教学的内容和要求发生了不少变化，在编排教材时，教材内容和编排顺序也就必然会随之发生变化，因此，我们在进行教学设计时，也应将这些变化体现在教学之中，让学生享受到教材调整带来的学习便利.我们应该站在教学的角度去认真解读教材，详细分析新、旧教材的点滴变化，并在新、旧教材的比对中发现教学的本质，探求高效教学的路径.通过上面的比对，我们发现本章内容从安排在一次函数之后调整到安排在二元一次方程之后，更有利于学生知识体系的建构；教材从山上温度随高度的变化到小丽骑车的速度变化，这一情境改进确实更接地气，更符合学生的认知水平；从“解不等式组”到“利用数轴探求不等式组的解集”这一设计的转变，体现出教材编排更能突出重点.

教材是课程标准得以落实的载体，是教师教与学生学的重要依据，因此，无论是教材编写者还是教材使用者，都应通过教材让课程转变为学生的认知目标，显然，通过比对新、旧教材来领悟课程标准的精神，不失为提高教学效率的一种有效方法.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］何永红．在新旧教材比对中设计教学［J］．中学数学（下半月），2015（3）：31-32.

韩新正（1968—），男，中学高级教师，主要从事课堂教学、教法和试题研究.

2016—02—09