基于动态种群多策略差分进化模型的多目标进化算法

王亚辉,吴金妹,贾晨辉

(1.华北水利水电大学机械学院,河南郑州 450011;2.河南科技大学机电工程学院,河南洛阳 471023)



基于动态种群多策略差分进化模型的多目标进化算法

王亚辉1,吴金妹1,贾晨辉2

(1.华北水利水电大学机械学院,河南郑州 450011;2.河南科技大学机电工程学院,河南洛阳 471023)

针对复杂的多目标优化问题,根据不同差分进化策略的特点,提出一种基于动态种群多策略差分进化模型和分解机制的多目标进化算法(MOEA/D-DPMD).该算法将种群划分为3个子种群,每个子种群分配一种差分进化策略.为了提高算法的性能,依据每种差分进化策略的贡献度,动态的调整子种群的规模,各差分进化策略之间相互配合协同进化.采用具有复杂的PS的LZ09系列基准函数,测试新算法的性能,仿真结果表明邻域规模为25时性能最好.通过不同差分进化策略之间的对比分析,新算法也具有较强的优势.将其与MOEAD/DE和NSGA-II算法对比分析,结果显示该算法的收敛性和多样性均优于另外两种算法,是求解复杂多目标问题的有效方法.

分解机制;多策略差分进化;动态种群;多目标优化

1　引言

多目标优化问题(Multi-objective Optimization Problem,MOP)在科学研究和工程应用领域广泛存在,是一类具有挑战性的优化问题.相对单目标问题而言,MOP目标之间相互冲突,难以得到最优解,而是一组折中的Pareto最优解集.传统的多目标优化算法将各个子目标聚合成单目标函数,其共同缺点就是一次运行只能得到一个Pareto最优解.由于进化算法在一次运行后能够获得一组Pareto最优解,因此进化算法在多目标优化领域的研究越来越多,国际上主流算法主要以NSGA-II[1],SPEA2[2],PAES[3],MOEA/D[4],IBEA[5],HypE[6]为代表.对于上述算法,根据评价关系大体可分为三类:(1)Pareto占优或变形的Pareto占优评价关系的MOEA算法,如NSGA-II,SPEA2,paε-MyDE[7]等;(2)基于性能指标的MOEA算法,采用HV性能指标,该类算法时间复杂度较高,如IBEA,HypE等;(3)基于分解机制的MOEA算法,如MOEA/D等.

基于分解技术的多目标进化算法(Multi-objective Optimization Evolutionary Algorithm,MOEA)是一类新的MOEA框架[4,8,9],该算法的研究主要从四个方面进行:(1)将MOEA/D算法同其他启发式算法相结合[10～13];(2)将新的分解机制融入到MOEA/D框架[14～16];(3)新的权重向量方法[17～20];(4)在MOEA/D中加入新重组或变异算子[9,21～23].

差分进化策略对提高算法的全局搜索能力和多样性有较好的效果[8,24].基于上述研究基础,本文提出一种新的基于分解和动态种群多策略差分进化模型的多目标优化算法(Multi-objective Evolutionary Algorithm Based on Dynamic Population Multi-strategy Differential Models and Decomposition,MOEA/D-DPMD).本文工作相对于文献[8]的工作的主要区别:(1)将种群划分了几个子种群,每个子种群分配一种差分进化策略,采用该种形式有两个好处:一者不增加算法的复杂度,二者可以形成多种差分进化策略的协同进化;(2)在进化过程中,为了避免某一次差分进化策略的进化停滞,影响算法整体的整体性能,从而将依据进化策略对更新邻域个体贡献度的不同,动态的调整每个子种群的规模.本文分析了不同进化代数,不同邻域大小和不同差分进化策略的对算法性能的影响.将MOEA/D-DPMD同MOEA/D和NSGA-II对比分析,实验结果表明新算法在收敛精度和收敛速度方面都取得了较好的效果.

2　基于动态种群多策略差分进化模型的多目标进化算法

2.1分解机制

分解机制[4]是由Zhang在MOEA/D中提出一种求解多目标问题的策略,其将MOP分解为一系列的子问题,然后利用单目标进化算法来求解每个子问题.在MOEA/D中,常用的分解方法有权重向量法[25]、切比雪夫法[26]以及边界插入法[24～27],其中以切比雪夫法应用最为广泛,其分解机制为:

subject tox∈Ω

每个子问题对应一个权重向量,子问题的邻居是通过计算每个权重向量与其欧式距离最小的T个权重向量来确定的.每一代种群由每个子问题的当前最优解构成,对每个子问题的进化操作被限制在邻居内进行.在每一代t,采用切比雪夫机制的MOEA/D保存的个体信息方式有:

(1)组成群体的N个点:x1,x2,…,xN∈Ω,其中xi为子问题i的当前最优解;

(2)FV1,FV2,…,FVN其中FVi=F(xi),i=1,2,…,N;

(3)z=(z1,z2,…,zm)T,其中zi为目标函数fi目前为止所找到的最优值;

2.2动态种群多策略差分进化模型

文献[8]中表明差分进化策略有利于提高MOEA/D算法的性能;文献[28]中多策略差分进化有利于提高算法的多样性和分布性,文中分析了不同进化策略的优劣.

本文选取3种差分进化模式:DE/rand/1/bin,DE/best/1/bin和DE/rand-to-best/1/bin,3种进化模式动态协同进化,其中3种进化模式的重组公式如下

(1)DE/rand/1/bin模式,其重组公式为:Vi=Xr1+F(Xr1-Xr2)

(2)DE/best/1/bin模式,其重组公式为:Vi=Xbest+F(Xr1-Xr2)

(3)DE/rand-to-best/1/bin模式,其重组公式为:

Vi=Xi+F(Xbest-Xi)+F(Xr1-Xr2)

其中DE/rand/1/bin模式中,随机选择一个个体Xr1为基准个体,并由Xr1与随机差分向量经过重组产生尝试个体Vi,其特性是全局搜索能力突出,具有较强的全局收敛性能并且不易陷入局部收敛,但是其收敛速度较慢;DE/best/1/bin模式中,基准个体是当前群体中的最优个体Xbest,通过Xbest与随机差分向量进行重组产生尝试个体Vi,该模式的全局搜索能力较弱,局部寻优能力和继承特性较强,收敛速度快但是容易陷入局部最优;在DE/rand-to-best/1/bin模式中,其以Xi为基准个体,产生固定差分向量(Xbest-Xi)和随机差分向量(Xr1-Xr2),然后将其线性组合得到尝试个体Vi,其特点是能够很好地保持全局搜索和局部寻优之间的平衡,对各类优化问题具有良好的适应性,但是鲁棒性较差.

各差分进化模式存在着搜索性能上的差异,但具有共通之处,即产生尝试个体的重组方式基本一致,都是通过将基准个体和差分向量进行线性组合而得到新的向量.但各种模式在结构及进化方式上的共通特性和搜索性能差异上的特点,使得共性与差异之间可以协同进化.

基于此,随机生成大小为N种群NP,将种群NP划分为三个子种群IA,IB和IC,使得个ξ1个体在子种群IA中,ξ2个个体在子种群中IB,ξ3个个体在子种群IC中,此时ξ1=ξ2=ξ3=N/3.将每个子种群分配一种进化模型,进行协同进化,其多策略差分进化过程为

fori=1:Ndo

ifi∈IA

DE/rand/1/bin操作产生子代个体yi

else ifi∈IB

DE/best/1/bin操作产生子代个体yi

else

DE/rand-to-best/1/bin操作产生子代个体yi

end for

如果IA,IB,IC的大小不改变,会存在一种不利算法进化的现象,即在进化过程中,若某一进化策略停滞将会导致算法的整体性能和效率的降低,因此本文采用动态子种群的方法,主要流程为:

(1)多策略差分进化,产生新的子代个体yi.

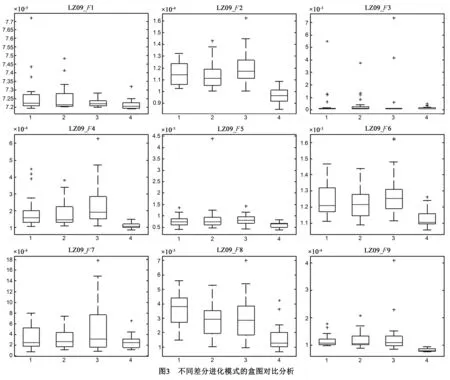
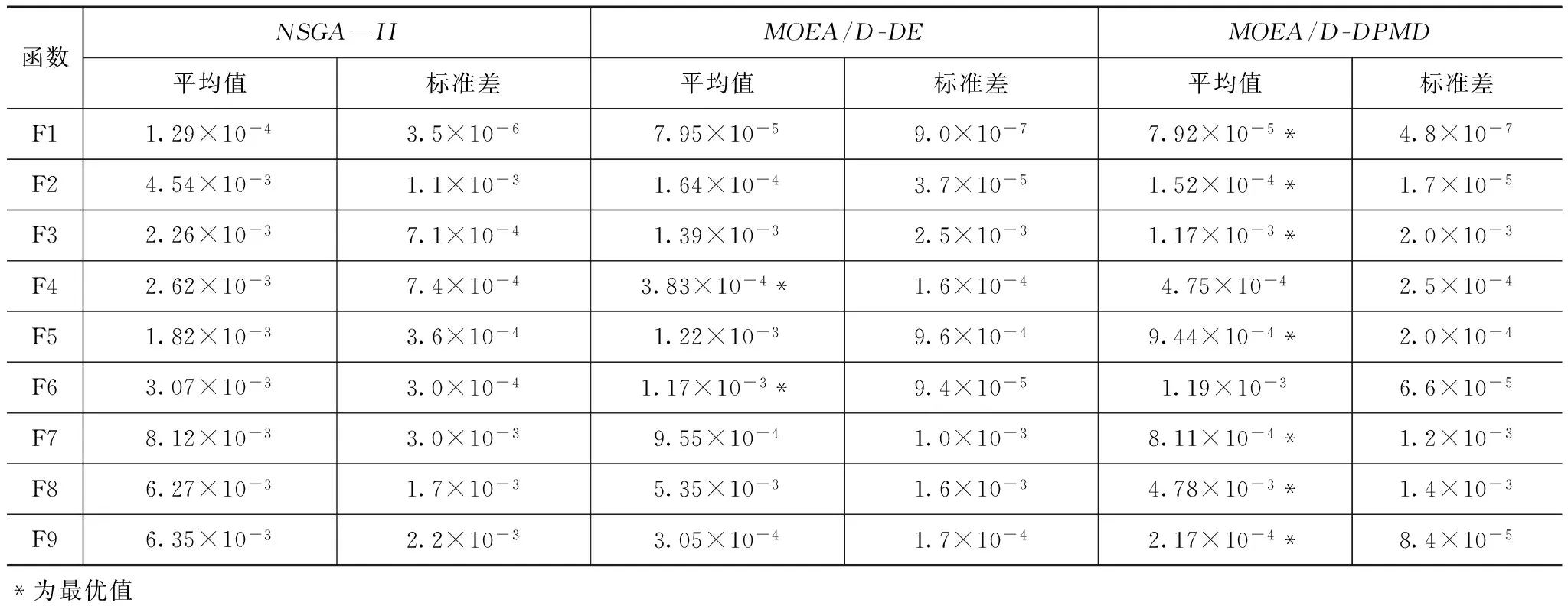
(2)更新参考点,若zj

(3)计算每种策略的进化成功率

其中,κi是指在第i个子种群中第i中策略产生的子代个体至少能在T个个体中更新一个个体的次数.

(4)重新计操作数种群的规模,其中ξ1=N×τ1,ξ2=N×τ2,ξ1=N-ξ1-ξ2,然后更新ξ1、ξ2和ξ3.

采用此种动态种群多策略差分进化策略,根据差分进化策略在进化过程的贡献,不断的动态的调整子种群的大小,这种进化方式提高算法的效率,保证了算法的收敛性,同时由于3种差分进化策略都参与进化,又利于算法的多样性.为了避免,在进化过程某一种差分进化策略强占优于其它2种策略,则给τ1,τ2,τ3定一个范围.如果τ<τmin,取τ=τmin;如果τ>τmax,取τ=τmax,其中τmax=0.8,τmin=0.15.

基于此,基于动态种群多策略差分进化模型的多目标进化算法(MOEA/D-DPMD)流程如下:

输入:

(1)多目标优化问题;

(2)停止准则;

(3)N:MOEA/D-DPMD所分解的子问题个数;

(4)λ1,λ2,…,λN:分布均匀的N个权重向量;

(5)T:权重向量的邻居规模;

(6)种群NP的大小为N;

Step1初始化

(1)设置EP=φ;

(2)计算任何两个权重向量的欧式距离,为每个权重向量选出最近的T个向量作为它的邻居.设B(i)={i1,i2,…,iT},i=1,2,…,N,其中λi1,λi2,…,λiT为距离λi最近的T个权重向量;

(3)初始化种群x1,x2,…,xN,设FVi=F(xi),i=1,2,…,N;

(4)随机将种群NP={1,2,…,N}分为三个子种群IA,IB,IC,使得ξ1个个体在子种群IA中,ξ2个个体在子种群IB中,ξ3个个体在子种群IC中,初始时设定ξ1=ξ2=ξ3=[N/3].

Step2动态协同差分进化

(1)协同差分操作,如3.2节所述;

(2)更新参考点.若zj

(3)更新子问题.若gte(yi|λk,z)≤gte(xk|λk,z)则xk=yi且F(xk)=F(yi),其中k∈B(i)={i1,i2,…,iT};

(4)计操作数代种群的贡献率,如3.2节所述;

(5)更新ξ1,ξ2,ξ3.

Step3停止判断:若G>Gmax,则停止算法并输出结果,否则返回到Step2.

2.3时间复杂度分析

为了评估MOEA/D-DPMD算法的计算效率,将其与MOEA/D-DE和NSGA-II进行对比分析.MOEA/D-DE在种群进化的过程中始终采用单一的DE算子,而MOEA/D-DPMD是动态的将种群分解为三个子种群然后对不同的种群采用不同的DE算子,两者具有相同的计算框架,故其时间复杂度相同.假设三种算法的种群大小均为N、目标数均为m.在单次迭代中,当利用DE算子进化得到新解后,需要更新参考点Z*和规模为T的邻居,因此MOEA/D-DE和MOEA/D-DPMD的时间复杂度为O(mNT).NSGA-II的时间开销主要用于其非支配排序操作,非支配排序需要将种群中的个体进行两两比较才能确定支配关系,因此其时间复杂度为O(mN2).由于邻居规模T小于种群规模N(T约等于0.1N～0.2N),因此MOEA/D-DPMD和MOEA/D-DE具有相同的时间复杂度,但是低于NSGA-II.

3　实验仿真与分析

为了检验MOEA/D-DPMD算法的有效性,本文使用文献[8]中提出的LZ09-F(1～9)系列基准函数,这9个函数具有复杂的PS,其中F6和F9为非凸PF,其它函数为凸函数,F7和F8为多峰问题,F1～F5和F7～F9为2目标函数,F6为3目标函数.

3.1性能指针

由于采用的测试函数均可得到其理论最优值,本文选取HV[29]与IGD[30]两个评价指针对算法性能进行综合评价.

3.2不同的进化代数的影响

表1是MOEA/D-DPMD对9个测试函数运算结果的IGD指针的统计结果.由表1中可见,随着计算代数的增加,IGD度量值显著减小,特别是100代至200代之间变化明显,但250代与300代的差距较小.经过300代计算,对于测试集LZ09具有复杂的PS和难以获得均匀的PF.图1为MOEA/D-DPMD算法获得的最终解集.由1(a)所示,对于F1～F4,F7和F9问题,算法获得的最优解PF都很好地逼近了真实PF解集,在F5和F8问题上存在少量的间断部分,F6问题上获得的PF较均匀,但在端点处有少许点没有完全收敛到端点.由1(b)可知,由于LZ09问题复杂的PS,算法的寻优过程较困难,但是MOEA/D-DPMD算法基本上都能有效逼近真实的PS.图1(c)和1(d)为MOEA/D-DPMD算法运行30次中获得所有的PF和PS值,由图可知算法获得解集能完全覆盖所有问题的PF和PS,且收敛性和多样性都较好,但在F8问题上PS收敛性稍差.

表1　不同进化代数G的MOEA/D-DPMD性能分析

3.3邻域大小对比分析

对于MOEA/D-DPMD算法中,邻域规模T的大小会对算法的收敛速度和多样性都有一定的影响[31].为了验证不同邻域大小对算法性能的具体表现,将邻域大小分为10,15,20,25,30进行对比分析.MOEA/D-DPMD的参数设定为:当2目标问题时种群大小为300,3目标时为500;最大计算代数G为250代;3个DE策略的控制参数均取CR=1.0,F=0.5;邻域搜索概率δ=0.9;多项式变异操作数参数η=20,Pm=1/Var,其中Var为决策变量长度.

对上述9个测试函数各独自运行30次,使用IGD进行评价.为了更准确的了解,采用Friedman进行统计分析邻域T的大小对算法性能的影响,其具体的表现如图2所示.由图2可知,在T=25时,算法的IGD值最小,因此综合考虑采用邻域T=25.

3.4不同的差分进化策略分析

MOEA/D-DPMD算法分别采用了三种差分进化策略协同进化,为了对比不同的差分进化模式对算法的影响,分别将不同的差分进化模式融入基于分解机制的多目标进化算法框架中,得到算法1,2,3,其中算法1为单独将DE/rand/1/bin策略融入MOEA/D算法框架中,算法2为单独将DE/best/1/bin策略,算法3单独将为DE/rand-to-best/1/bin策略,算法4为MOEA/D-DPMD算法.

四种算法的参数设置为:对于2目标问题,种群规模为300,对于3目标问题,种群的规模为500,迭代次数为250.三种差分模式中,CR和F均分别设置为1.0和0.5,多项式变异操作数参数η=20,Pm=1/Var,其中Var为决策变量长度.四种算法对每个问题均连续独立运行30次,利用盒图来表示算法对各测试问题的实验统计结果.从图3来看,在F1～F9上,MOEA/D-DPMD所得到的PF均最为集中,表明在30次独立运行中,其所得到的结果非常稳定.并且,MOEA/D-DPMD所得到的数据的中位值均小于其它三种单独策略的算法所得到的中位值,表明其收敛性和覆盖性均优于其它三种算法,尤其是在F(1,2,4,6,8,9)上优势更为明显.进一步分析可知,仅仅采用一种差分策略时,算法所得到的中位值和上下四分位比较接近,说明3种算法的性能大致相当,但是采用协同进化机制的MOEA/D-DPMD的性能有了较大程度的提升.由此可说明:1)采用协同进化机制的MOEA/D-DPMD相比采用单一差分策略的算法而言,其所得的Pareto前端更加逼近真实的Pareto前端9且分布均匀,其性能有了较大程度的提升;2)协同进化的MOEA/D-DPMD的鲁棒性更强,能够更好地求解各类具有不同PS的复杂优化问题.

3.5算法对比实验

本节比较MOEA/D-DPMD算法与NSGA-II[1]和MOEA/D-DE[8]算法,其中3种算法的计算代数为250代,对于2目标问题种群NP大小为300,对于3目标问题时为500,其中所有DE策略的控制参数均取CR=1.0,F=0.5,多项式变异操作数参数η=20,Pm=1/Var,其中Var为决策变量长度.MOEA/D-DPMD算法和MOEA/D其它参数为:邻域大小T=25,邻域搜索概率δ=0.9;NSGA-II算法其它参数为:SBX[32]交叉概率Pc=0.9.对每个测试函数均独立运行30次,然后统计指标HV、和IGD的均值和标准差,所得结果如表2～3所示.

由表2可知,MOEA/D-DPMD算法获得了6个最优值,MOEA/D-DE获得了3个最优值,NSGA-II算法未获得最优值.F1,F4和F6问题上,MOEA/D-DE取得较好的结果,对于F2,F3,F5和F7～F9问题上MOEA/D-DPMD性能最好,NSGA-II未取得较好的结果.其中对于F1和F4,MOEA/D-DE所获得的HV均值同MOEA/D-DPMD所获得均值相等,仅方差上取胜.

由表3可知,9个测试函数中MOEA/D-DPMD算法获得了7个最优值;MOEA/D-DE获得2个最优值;NSGA-II不能取得较好值.资料分析表明,在F4问题上,MOEA/D-DE性能较好,MOEA/D-DE所得结果的IGD均值是MOEA/D-DPMD所得均值的1.24倍;对于F3,F5,F7～F9问题上,MOEA/D-DPMD所得结果的IGD均值分别是MOEA/D-DE所得均值的1.19,1.29,1.18,1.12,1.41倍;对于F1,F2和F6问题,两算法获得结果接近.

表2　HV标准平均值及方差

表3　IGD标准平均值及方差

综合以上分析我们可以得出结论,MOEA/D-DPMD与MOEA/D-DE、NSGA-II相比,具有较强的竞争力.

4　总结

本文在MOEA/D算法框架下,将一种动态种群多策略差分进化模型融入框架中,提出一种基于动态种群多策略差分进化模型和分解机制的多目标进化算法(MOEA/D-DPMD).该算法将种群划分为几个子种群,每个子种群分配一种DE策略,在进化过程中,根据不同DE策略对种群的贡献度,动态的分配下一代DE策略作用的子种群的规模,多种DE策略相互配合,协同进化.通过实验分析结果表明:

(1)MOEA/D-DPMD算法的邻域T大小为25时,综合性能最好;

(2)不同的差分进化模型对比分析,可知动态种群多策略差分进化模型较单差分进化策略的所获得的解更逼近真实的PF且分布均匀,其性能有了较大程度的提升;

(3)同MOEA/D-DE和NSGA-II对比,MOEA/D-DPMD在收敛性和覆盖性要优于其它两种算法.在进化中的IGD平均值对比,表明同样情况下,MOEA/D-DPMD所需要的评价次数要低于其它两种算法.下一步的研究方向为,将其进一步修正用于求解高维多目标优化问题和含有约束问题工程实际问题中.

[1]Deb K,Pratap A,Agarwal S,et al.A fast and elitist multi-objective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

[2]Zitzler E,Laumanns M,Thiele L.SPEA2:Improving the strength Pareto evolutionary algorithm for multi-objective optimization[A].Proceedings of the Evolutionary Methods for Design,Optimization and Control[C].Athens:International Center for Numerical Methods in Engineering,2002.95-100.

[3]Knowles J D,Corne D W.Approximating the non-dominated front using the Pareto archive evolution strategy[J].Evolutionary Computation,2000,8(2):149-172.

[4]Zhang Q,Li H.MOEA/D:A multi-objective evolutionary algorithm based on decomposition[J].IEEE Transactions on Evolutionary Computation,2007,11(6):712-731.

[5]Zitzler E,Kunzli S.Indicator-based selection in multiobjective search[J].Proc of the Parallel Problem Solving from Nature (PPSN VIII)[C].Berlin,Heidelberg:Springer-Verlag,2004.LNCS 3242,832-842.

[6]Bader J,Zitzler E.HypE:An algorithm for fast hypervolume-based many-objective optimization[J].Evolutionary Computation,2011,19 (1):45-76.

[7]Hernadez-Diaz AG,Santana-Quintero LV,Coello Coello CA,Molina J.Pareto-Adaptive ε-dominance[J].Evolutionary Computation,2007,15(4):493-517.

[8]Li H,Zhang Q.Multi-objective optimization problems with complicated Pareto sets,MOEA/D and NSGA-II[J].IEEE Transactions on Evolutionary Computation,2009,13(2):284-302.

[9]周爱民,张青富,张桂戌.一种基于混合高斯模型的多目标进化算法[J].软件学报,2014,25(5):913-928.

Zhou Ai-min,ZHANG Qing-fu,ZHANG Gui-xu.Multi-objective evolutionary algorithm based on mixture Gaussian models[J].Journal of Software,2014,25(5):913-928.(in Chinese)

[10]H Li,D Landa-Silva.An adaptive evolutionary multi-objective approach based on simulated annealing[J].Evolutionary Computation,2011,19(4):561-595.

[11]N Moubayed,A Petrovski,J McCall.A novel smart multi-objective particle swarm optimization based on decomposition[A].International Conference on Parallel Problem Solving from Nature[C].Berlin Heidelberg:Springer,2010.1-10.

[12]Z Martinez,C Coello Coello.A multi-objective particle swarm optimizer based on decomposition[A].Genetic and Evolutionary Computation Conference[C].New York:ACM,2011.69-76.

[13]王亚辉,贾晨辉,赵仁鹏.基于分解机制的多目标蝙蝠算法[J].农业机械学报,2015,46(4):316-324.

Wang Yahui,Jia Chenhui,Zhao RenPeng.Multi-objective bat algorithm based on decomposition[J].Transactions of the Chinese Society for Agricultural Machinery,2015,46(4):316-324.(in Chinese)

[14]Q Zhang,H Li,D Maringer,E Tsang.MOEA/D with NBI-style Tchebycheff approach for portfolio management[A].IEEE Congress on Evolutionary Computation[C].Barcelona:IEEE,2010.1-8.

[15]H Ishibuchi,Y Sakane,N Tsukamoto,Y Nojima.Adaptation of scalarizing functions in MOEA/D:An adaptive scalar zing function-based multi-objective evolutionary algorithm[A].International Conference on Evolutionary Multi-Criterion Optimization[C].Berlin Heidelberg:Springer,2009.438-452.

[16]H Ishibuchi,Y Sakane,N Tsukamoto,Y Nojima.Simultaneous use of different scalarizing functions in MOEA/D[A].Genetic and Evolutionary Computation Conference[C].New York:ACM,2010.519-526.

[17]Y Tan,Y Jiao,H Li,X Wang.MOEA/D + uniform design:a new version of MOEA/D for optimization problems with many objectives[J].Compute Opera Res,2013,40(6):1648-1660.

[18]X Ma,Y Qi,L Li,F Liu,et al.MOEA/D with uniform decomposition measurement for many-objective problems[J].Soft Compute,2014,18:2541-2564.

[19]F Gu,H Liu.A novel weight design in multi-objective evolutionary algorithm[A].International Conference on Computational Intelligence and Security[C].Nanning:IEEE,2010.137-141.

[20]Y Qi,X Ma,F Liu,L Jiao,et al.MOEA/D with adaptive weight adjustment[J].Evolutionary Computation,2014,22(2):231-264.

[21]C Chen,Q Zhang.Enhancing MOEA/D with guided mutation and priority update for multi-objective optimization[A].IEEE Congress on Evolutionary Computation[C].Trondheim:IEEE,2009.209-216.

[22]W Huang,H Li.On the differential evolution schemes in MOEA/D[A].International Conference on Natural Computation[C].Yantai:IEEE,2010.2788-2792.

[23]H Li,D Landa-Silva.An adaptive evolutionary multi-objective approach based on simulated annealing[J].Evolutionary Computation,2011,19 (4):561-595.

[24]毕晓君,肖婧.基于自适应差分进化的多目标进化算法[J].计算机集成制造系统,2011,17(12):2660-2665.

Bi Xiao-jun,Xiao Jing.Multi-objective evolutionary algorithm based on self-adaptive differential evolution[J].Computer Integrated Manufacturing Systems,2011,17(12):2660-2665.(in Chinese)

[25]Miettinen K.Nonlinear Multi-objective Optimization.Norwell[M].MA:Kluwer,1999.

[26]Das I,J E Dennis.Normal-boundary intersection:A new method for generating Pareto optimal points in multi-criteria optimization problems[J].SIAM J Optim,1998,8(3):631-657.

[27]Messac A,Ismail-Yahaya,C Mattson.The normalized constraint method for generating the Pareto frontier[J].Struct Multidisc Optim,2003,25:86-98.

[28]詹腾,张屹,朱大林,刘铮,等.基于多策略差分进化的元胞多目标遗传算法[J].计算机集成制造系统,2014,20(6):1342-1351.

Zhan Teng,Zhang Yi,Zhu Da-lin,Liu Zheng,et al.A cellular genetic algorithm based on multi-strategy differential evolution for multi-objective optimization[J].Computer Integrated Manufacturing Systems,2014,20(6):1342-1351.(in Chinese)

[29]Zitzler E,Thiele L.Multi-objective evolutionary algorithms:a comparative case study and the strength Pareto approach[J].IEEE Transactions on Evolutionary Computation,1999,3(4):257-271.

[30]Bosman T,Thierens D.The balance between proximity and diversity in multi-objective evolutionary algorithms[J].IEEE Transactions on Evolutionary Computation,2003,7(2):174-188.

[31]Ishibuchi H,Akedo N,Nojima Y.Relation between neighborhood size and MOEA/D performance on many-objective problems[A].Evolutionary Multi-Criterion Optimization[C].Berlin Heidelberg:Springer,2013.459-474.

[32]DEB K,AGRAWAL R B.Simulated binary crossover for continuous search space[J].Complex Systems,1995,9(2):115-148.

王亚辉女,1970年出生,河南濮阳人,副教授、硕士生导师,主要从事先进制造技术和现代设计方法研究工作.

E-mail:wangyahui@ ncwu.edu.cn

吴金妹女,1976年生,海南屯昌人,讲师,主要从事机械设计制造及设备方面的研究工作.

E-mail:wujinmei@ ncwu.edu.cn

贾晨辉男,1970年11月出生,博士、副教授、硕士研究生导师.主要研究方向为:计算机集成制造技术、系统工程、虚拟样机设计技术、机器人技术的研究工作.

Multi-objective Evolutionary Algorithm Based on Dynamic Population Multi-strategy Differential Models

WANG Ya-hui1,WU Jin-mei1,JIA Chen-hui2

(1.SchoolofMechanicalEngineering,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou,Henan450011,China;2.SchoolofMechatronicsEngineering,HenanUniversityofScienceandTechnology,Luoyang,Henan471023,China)

According to the characteristics of differential evolution,a multi-objective evolutionary algorithm based on dynamic population multi-strategy differential models and decomposition (MOEA/D-DPMD) is proposed to solve the expensive problems.The algorithm divides the population into three sub-populations and each sub-population is corresponding to a differential evolution strategy.In order to improve the performance of the algorithm,the size of sub-population is adjusted dynamically on the basis of a differential evolution strategy contribution.Each strategy is adopted to participate in coordination during the evolution process.Through the test simulation on the LZ09 benchmarks with complicated Pareto Set (PS),MOEA/D-DPMD shows a best performance with a neighborhood size of 25.Via the comparative analysis of different schemes of differential strategy,MOEA/D-DPMD also performs well.The experimental results indicate that MOEA/D-DPMD has a better performance in terms of convergence and diversity compared with MOEA/D and NSGA-II,which is an effective way for solving complex multi-objective optimization problems.

decomposition mechanism;multi-strategy differential evolution;dynamic population;multi-objective optimization

2015-05-11;修回日期:2015-09-20;责任编辑：李勇锋

国家自然科学基金(No.51475142)

TP18

A

0372-2112 (2016)06-1472-09