基于贝叶斯压缩感知的FD-MIMO雷达Off-Grid目标稀疏成像

王天云,陆新飞,丁　丽,尹治平,陈卫东

(1.中国卫星海上测控部,江苏江阴 214431;2.中国科学技术大学中科院电磁空间信息重点实验室,安徽合肥 230027;3.合肥工业大学光电技术研究院,安徽合肥 230009)



基于贝叶斯压缩感知的FD-MIMO雷达Off-Grid目标稀疏成像

王天云1,2,陆新飞2,丁丽2,尹治平3,陈卫东2

(1.中国卫星海上测控部,江苏江阴 214431;2.中国科学技术大学中科院电磁空间信息重点实验室,安徽合肥 230027;3.合肥工业大学光电技术研究院,安徽合肥 230009)

传统压缩感知(CS,Compressive Sensing)成像方法一般假定目标精确位于事先划定的成像网格上，实际中由于散射点空间位置是连续分布的，因此偏离网格(Off-grid)问题必然存在.这会引起真实回波测量值与默认系统观测矩阵之间失配，导致传统CS成像方法性能恶化.本文基于频率分集多输入多输出(FD-MIMO,Frequency Diverse Multiple-Input Multiple-Output)雷达，针对Off-grid目标提出了一种基于贝叶斯压缩感知的稀疏自聚焦(SAF-BCS,Sparse Autofocus Imaging Method Based on Bayesian Compressive Sensing)成像算法.该算法依据最大后验(MAP,Maximum A Posteriori)准则，利用变分贝叶斯学习技术求解含有Off-grid目标的稀疏像.与传统稀疏重构方法相比，所提方法充分利用了目标先验信息，可自适应调整参数，能够更好地反演稀疏目标，同时具有校正Off-grid目标的网格位置偏差以及估计噪声功率等优势.仿真结果表明SAF-BCS算法对网格划分不敏感，具有稳健的成像性能.

贝叶斯压缩感知；FD-MIMO雷达；Off-grid目标；变分贝叶斯学习；稀疏自聚焦成像

1　引言

多输入多输出(MIMO)雷达是一种采用多发射天线、多接收天线的雷达系统，通过利用发射信号的正交特性获得波形分集增益，以及利用发射机和接收机之间相对目标的空间展开特性获得空间分集增益，可以有效地提升雷达成像性能[1].频率分集MIMO(FD-MIMO)雷达通过合理设计不同发射机的信号频率，可以等效为辐射大带宽的雷达信号，进一步提高距离分辨率，已逐渐成为新型MIMO雷达成像系统的一个重要研究方向[2].

随着人们对雷达成像分辨率的要求越来越高，以奈奎斯特采样定理为基础的传统雷达信号处理技术对数据采样及处理速率的要求也越高，使得雷达系统的结构也更加复杂.作为近年来信号处理领域的新兴技术，压缩感知(CS,Compressive Sensing)理论利用目标稀疏先验信息，在远低于奈奎斯特速率采样率情形下，只需要少量观测样本即可重构原始信号，可以有效减少雷达系统的数据采样时间和数据量[3].因此，在实际系统受限的情形下，利用CS成像方法可以进一步提高目标的空间分辨率，目前在SAR成像，ISAR成像，MIMO雷达成像等领域已有较多研究[4].现有CS成像方法[5]，首先需要对成像场景进行离散化获得相应的观测矩阵，并假定目标散射点精确位于预先划定的网格上.实际中由于待求解的目标散射点的空间位置是连续的，可以为任意值，因此不可避免存在偏离网格(Off-grid)目标.于是依据离散化成像场景构造的观测矩阵与真实回波之间会存在失配现象(即文献[6～14]所讨论的Off-grid问题)，导致传统稀疏重构方法性能下降.文献[6]基于实测数据分析了探地雷达中Off-grid目标对传统CS成像方法的影响，实验结果表明不合理的网格划分会造成传统CS成像方法性能的严重恶化.文献[7～9]则分别讨论了无源雷达、SAR和ISAR中的Off-grid问题，并得到类似的结论.

虽然通过“精细化网格”可以降低观测矩阵的失配程度，但是该方法不能从本质上解决Off-grid问题，因为太细的网格会减弱观测矩阵的RIP性质，导致反演结果的不稳定性[10].目前常见的解决办法是采用Off-grid CS方法[11～14]，它修正了传统CS方法求解连续空间稀疏信号模型，通过同时求解待反演目标和网格误差，增强了基于CS技术提取目标信息的稳健性.文献[11，12]将网格误差因素的影响用扰动矩阵近似，并假定扰动矩阵服从高斯分布，分别提出了BCS-LASSO和TLS-FOCUSS反演算法；文献[13，14]则将网格误差因素的影响用一阶泰勒展开模型近似，并假定网格位置偏差服从均匀分布.考虑实际情形，这种假设[13，14]要比高斯分布假设[11，12]更为合理.其中文献[13]针对DOA中的Off-grid问题，选取了二级分层形式的目标稀疏先验模型，并基于Type-II最大似然(ML,Maximum Likelihood)理论提出OGSBI算法.文献[14]则研究了FD-MIMO雷达中的Off-grid问题，将待求解信号建模为lp范数稀疏模型，提出了基于最大后验(MAP,Maximum A Posteriori)准则的稀疏自适应校正反演算法(SACR-iMAP)，相比文献[13]具有更快的收敛速度和求解精度.

本文以FD-MIMO雷达作为研究基础，提出了一种基于贝叶斯压缩感知的稀疏自聚焦成像(SAF-BCS)算法，能有效地克服回波方程中因Off-grid目标带来的“乘性”扰动和“加性”扰动.文中首先建立三级分层形式的目标稀疏先验模型(是对文献[15]的拓展)，相比文献[13]中的两级稀疏模型以及文献[14]中的lp范数稀疏模型，能获得更好的对l0范数近似度，即可以表征更稀疏的目标信息；其次在基于MAP准则求解目标参数的后验概率密度函数时，采用变分贝叶斯期望最大化(VBEM,Variational Bayesian Expectation Maximization)算法[16]实现对后验概率分布近似的解析求解，不仅可以避免EM等传统贝叶斯推断算法不再适用的缺点，而且可以得到较好的参数估计效果.此外，与传统CS成像方法相比，所提算法充分利用了目标、噪声以及网格误差的统计信息，具有自适应调整参数，可同时获得目标成像结果、网格位置偏差以及噪声功率等相关参数的优势.仿真表明，SAF-BCS对网格划分不敏感，在相同系统配置模式下，其成像结果优于传统CS方法(FOCUSS[9])，TLS-FOCUSS[12]和SACR-iMAP[14].

2　FD-MIMO雷达Off-grid目标成像模型

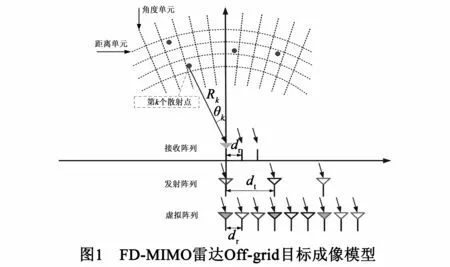
本文研究的FD-MIMO雷达成像系统如图1所示，由M个发射阵元，N个接收阵元组成.发射机阵列、接收机阵列与成像区域位于同一平面，且为均匀线阵，阵元间距分别为dt和dr.假定成像场景中共有K个强散射点组成，其中第k个散射点对应的复散射系数、距离单元和角度单元分别为σk,Rk,θk.

假设各发射阵元同时发射具有相同调频率的线性调频(LFM)信号，其中第m路发射信号为[2]

(1)

其中T为脉宽，γ为调频率，fm为第m路发射阵元的载频，且满足fm-fm-1=B.考虑到后续采用稀疏成像方式，所以发射信号带宽可以不必太高，这里B≪fm，因此有λm≈λ1≜λ，这里λ定义为系统工作波长.

(2)

(3)

定义发射信号矢量s(t)=[s1(t),s2(t),…,sM(t)]，c为光速.假设目标处于雷达远场，则接收的目标回波为

(4)

对式(4)采用阵列信号处理中的通道分离技术[14]，可以得到发射阵元m和接收阵元n对应的“虚拟收发通道”信号为

(5)

进一步，设发射阵元m对应的解线性调频的参考信号为sm(t-2R0/c)，则有如下近似关系

(6)

(7)

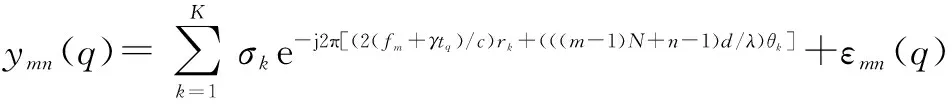
(8)

下面对成像场景进行均匀网格划分，包括U个距离单元和V个角度单元.由于目标位置空间(rk,θk)是连续的，因此真实的散射点一般不会精确位于预先划定的成像网格上.这将引起回波测量值与观测矩阵之间失配，导致传统CS成像方法性能严重恶化[14].

考虑网格误差的影响，式(8)应转化为

ymn(q)

+εmn(q)

(9)

其中(ru,θv)为假定网格点的位置，δru,δθv为真实散射点与假定网格点之间的网格位置偏差.

将二维成像场景转换至列向量形式，即σi=σu,v,i=(u-1)*V+v.利用二元函数Taylor展开公式并忽略高阶项的影响，回波方程最终整理为

y=(H+H1Δr+H2Δθ)σ+ε

(10)

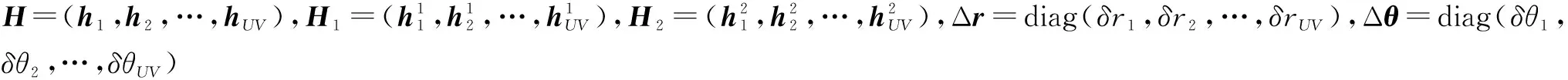
(11)

(12)

(13)

这里⊙表示Hadamard积.可见相比传统成像模型，由于Off-grid目标的存在，式(10)所示的回波方程引入了扰动矩阵H1Δr和H2Δθ，它们对目标信息矢量σ的影响是“乘性”扰动.传统CS成像方法仅对噪声等“加性”扰动进行了约束，并没有考虑“乘性”扰动的影响，因此无法获得稳健的目标反演结果.本文基于贝叶斯压缩感知理论框架，提出了一种能有效降低“乘性”扰动和“加性”扰动的稀疏自聚焦成像算法.该算法能有效地校正网格位置偏差Δr及Δθ的影响，从而更好地重构目标图像σ.

3　基于贝叶斯压缩感知的稀疏自聚焦成像

3.1目标参数贝叶斯压缩感知模型

3.1.1目标稀疏模型

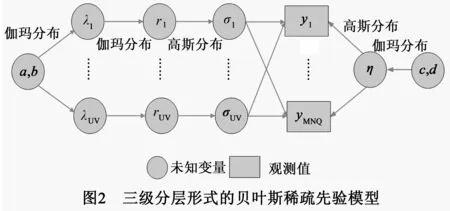
目前表征目标稀疏先验信息的方式主要包括确定性模型和贝叶斯模型两类.从本质上讲，确定性模型可以用合适的概率密度函数转换成贝叶斯模型，例如文献[18]阐述了l1范数约束条件在贝叶斯理论体系下的对应关系.本文提出了一种三级分层形式的贝叶斯稀疏先验模型(如图2所示)，具体描述为：

(1)首先σ服从均值为零，方差为Λ=diag{γ1,…,γUV}的复高斯分布，即σ～CN(0,Λ)，具体表示为

(14)

(2)其次γ服从伽马(Gamma)分布(因为它与高斯分布共轭，便于后续求解).

(15)

(3)最后λ服从伽马(Gamma)分布

(16)由式(14)，式(15)和式(16)可知，本文的目标稀疏先验模型是文献[15]的推广，具有更多的自由度可供调节：这里γ分布增加了UV-1个超参数，λ分布增加了1个超参数.再根据文献[15]的结论，相比传统稀疏先验模型(如l1,lp范数约束)，所提目标稀疏模型能得到对l0范数更好的近似度，因此可表征更稀疏的目标信息.

3.1.2噪声模型

设噪声模型服从复高斯分布CN(0,η-1Ι)，其中η-1表示噪声功率，为未知确定参数.则回波信号y对应的条件概率密度函数为

(17)

另外，为获得高斯分布函数的共轭特性[18]，再假定η服从伽马(Gamma)分布

p(η|c,d)=Γ(η|c,d)

(18)

3.1.3网格位置偏差模型

最后，假设真实散射点与假定网格点上目标之间的位置偏差Δr及Δθ满足均匀分布[13，14]，即

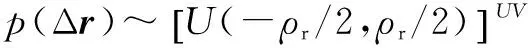
(19)

这里U(·)表示均匀分布，ρr和ρθ分别为距离维和角度维的网格间距，其划分准则由空间谱填充对应的极限分辨率来决定[2]，据此成像场景大小可表示为Uρr×Vρθ.

3.2基于贝叶斯压缩感知的稀疏自聚焦成像算法

根据式(10)、式(14)～(19)，目标散射系数σ，网格位置偏差{Δr,Δθ}，噪声功率的倒数η以及系统参数Λ,γ,a,b,c,d对应的联合概率密度函数表示为

p(y,σ,Δr,Δθ,γ,λ,η)

=p(y|σ,Δr,Δθ,η)p(σ|γ)·p(γ|λ)p(λ)p(η)p(Δr)·p(Δθ)

(20)

在贝叶斯压缩感知理论体系下，通常是基于最大后验(MAP)准则求解上述未知参数，即

p(σ,Δr,Δθ,γ,λ,η|y)=p(y,σ,Δr,Δθ,γ,λ,η)/p(y)

(21)

由于p(y)=∮p(y,σ,Δr,Δθ,γ,λ,η)dσdΔrdΔθdγ

dλdη积分结果难以直接求出，故无法得到式(21)对应的后验概率密度函数的解析表达式.因此本文采用变分贝叶斯期望最大化(VBEM)算法[16]来求解上述问题.VBEM算法的核心思想是通过寻找后验概率密度函数的近似分布，并且该近似分布存在闭合形式的解，使得KL散度最小，如式(22)所示.

p(σ,Δr,Δθ,γ,λ,η|y)≈q(σ,Δr,Δθ,γ,λ,η|y)

≜q(σ)q(Δr)q(Δθ)

·q(γ)q(λ)q(η)

(22)

这里将{σ,γ,λ,η}建模为参数，{Δr,Δθ}建模为隐含变量，利用VBEM算法求解式(22)对应的优化问题包括期望和最大化两个步骤.

3.2.1期望步骤——更新参数

(1)对于σ，根据

Inq(σ)=

〈Inp(y|σ,Δr,Δθ,η)p(σ|γ)〉q(Δr)q(Δθ)q(γ)q(λ)q(η)+Const

(23)

将式(14)与式(17)代入式(23)，经推导得到q(σ)服从复高斯分布CN(μ,Σ)，其中

μ=〈η〉Σ AHy

(24)

(25)

上式中A≜H+H1〈Δr〉+H2〈Δθ〉.

(2)对于γ，根据

Inq(γ)=〈Inp(σ|γ)p(γ|λ)〉q(σ)q(λ)+Const

(26)

将式(14)、式(15)代入式(26)，经整理得到q(γi)服从广义逆高斯(GIG,Generalized Inverse Gaussian)分布[19].

(27)

于是γi对应的k阶矩为

(28)

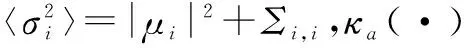
(3)对于λ，根据

Inq(λ)=〈Inp(γ|λ)p(λ)〉q(γ)+Const

(29)

将式(15)和式(16)代入式(29)，可以推导得到q(λi)服从伽马(Gamma)分布

(30)

其均值为

(31)

(4)对于η，根据

Inq(η)=〈Inp(y|σ,Δr,Δθ,η)p(η)〉q(σ)q(Δr)q(Δθ)+Const

(32)

将式(17)、式(18)代入式(32)，经推导可以得到q(η)服从伽马(Gamma)分布

(33)式中A的含义与式(24)及式(25)一致.另外定义tr(·)表示矩阵求迹运算，由式(33)求得〈η〉的估计结果为

(34)

3.2.2最大化步骤——更新隐含变量

(1)对于Δr，根据

(35)

将式(17)、式(19)代入式(35)，令wr≜diag(Δr)，B1=H+H2〈Δθ〉，经推导可得

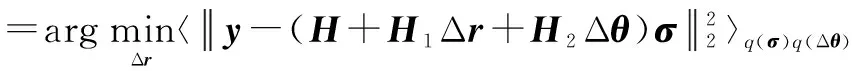
s.t.wr∈(-ρr/2,ρr/2)UV

(36)

其中

(37)

(38)

式(38)中Re(·)表示取实部操作.另外考虑到Δθ与σ非零元素的位置一致(即二者是联合稀疏)，因此式(36)应修正为

(39)

为了提高算法运算性能，这里采用文献[13]中的方法代替CVX软件包[20]求解式(39).

(2)同理，对于Δθ，根据

(40)

将式(17)、式(19)代入式(40)中，令wθ≜diag(Δθ)，B2=H+H1〈Δr〉，与式(39)推导过程类似，角度维网格位置偏差的更新准则如式(41)所示.

(41)

其中

(42)

(43)

3.2.3算法流程

首先需要进行参数初试化.即在迭代次数l=0时，获得关于参数σ,Δr,Δθ,γ,λ,η的初始估计.其中σ(0)利用匹配滤波(MF,Matched Filter)方法获得

(44)

另外，在σ(0)基础上得到噪声功率倒数的初始估计η(0)为

(45)

其余参数设置为

(46)

接着令l=l+1，通过交替更新期望步骤和最大化步骤，实现对未知变量的迭代求解.程序终止条件为：循环次数达到预先设定的值L或者相邻两次目标反演结果不再有较大变化.

综上，本文所提的稀疏自聚焦成像(SAF-BCS)算法流程如下所示.由于VBEM方法至少能保证获得局部最优解[16]，可知SAF-BCS是收敛的，相关参数的估计值随迭代次数增加而逐渐减小.

算法1SAF-BCS算法流程

输入：y,H,H1,H2

初始化：迭代次数l=0,σ(0),η(0),Δr(0),Δθ(0),γ(0),λ(0),a,b,c,d分别依据式(44)～(46)获得.

循环迭代：令l=l+1

(1)依据式(24)和式(25)更新目标散射系数σ(l)的均值μ和方差Σ.

(2)依据式(28)更新参数γ(l).

(3)依据式(31)更新参数λ(l).

(4)依据式(34)更新噪声功率的倒数η(l).

(5)依据式(39)估计距离维网格位置偏差Δr(l).

(6)依据式(41)估计角度维网格位置偏差Δθ(l).

(7)判断是否满足程序终止条件，若满足则输出结果，否则程序跳转至步骤(1).

4　仿真结果与分析

这里通过如下2组仿真实验来验证SAF-BCS成像方法的性能.其中FD-MIMO雷达的系统参数设置如表1所示.结合式(8)，图3(a)给出其空间谱填充结果[2]，据此可计算出匹配滤波成像方法的距离维和角度维极限分辨率约为ρr=1m,ρθ=0.01rad.下文考虑目标散射点的空间位置在成像区域内任意分布时，将SAF-BCS与MF，传统CS方法(FOCUSS[9])和Off-grid CS方法(TLS-FOCUSS[12],SACR-iMAP[14])进行比对，以验证其有效性.

表1　FD-MIMO雷达相关参数

实验1不同方法成像结果对比

图3(b)～3(f)是SNR=20dB时不同方法的成像结果，其中绿色圆圈代表原始成像目标，由8个幅值为1的强散射点组成，处于Off-grid状态.可以看出，图3(b)的“虚像”最多，这是因为MF基于傅里叶重构技术，分辨率受限于空间谱的填充(如图3(a)所示，由于空间谱支撑域的数据大面积缺失，导致该方法具有较高的旁瓣和较宽的主瓣).图3(c)是FOCUSS的重构结果，由于它没有考虑Off-grid问题，因此其成像性能较差.图3(d)～3(f)是三种Off-grid CS方法的成像结果.其中TLS-FOCUSS虽然考虑了校正Off-grid误差，但它依赖于网格位置偏差服从高斯分布，这与实际情形不符，故图3(e)成像质量有较大程度下降.根据前面分析，相比SACR-iMAP，SAF-BCS由于采用了级联形式的目标稀疏先验模型，可获得更好的对l0范数近似度；另外它基于VBEM技术求解目标参数贝叶斯压缩感知模型，可获得更好的参数估计效果，因此图3(f)的成像结果要优于图3(e).

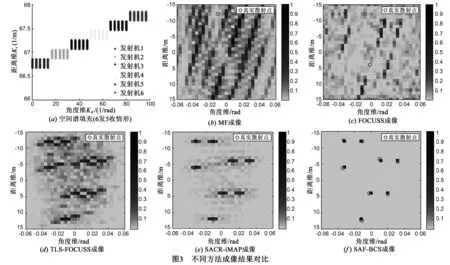
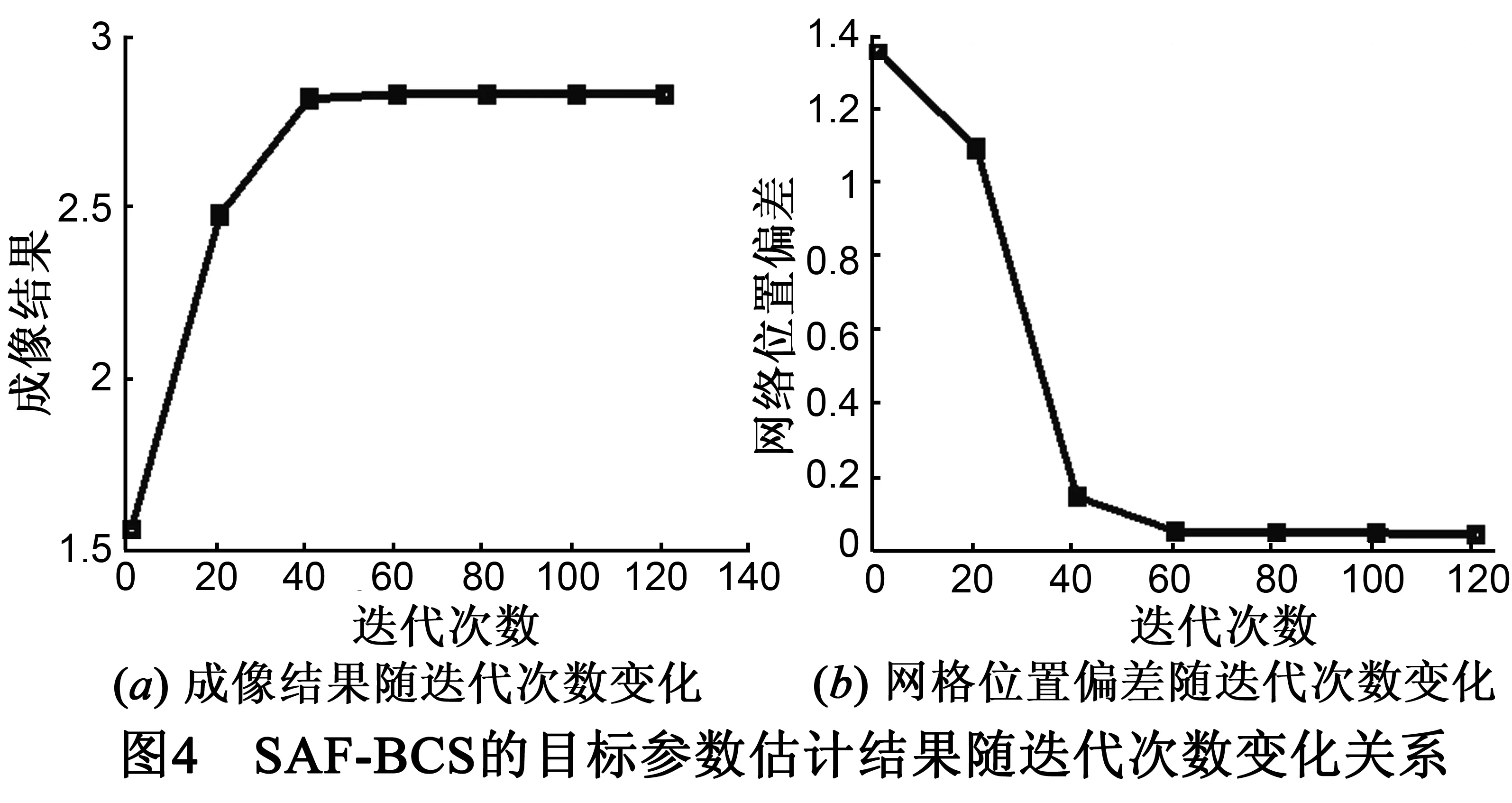
图4展示了SAF-BCS的成像结果(取2范数)、网格位置偏差(距离维与角度维的2范数之和)的估计结果随迭代次数的变化关系，可以看出所提算法具有较好的收敛特性.

实验2不同方法的成像误差及位置误差与“SNR、稀疏度”之间关系

定义成像误差、位置误差[9]分别为

(47)

其中G=30为蒙特卡洛(Monte Carlo)实验次数.

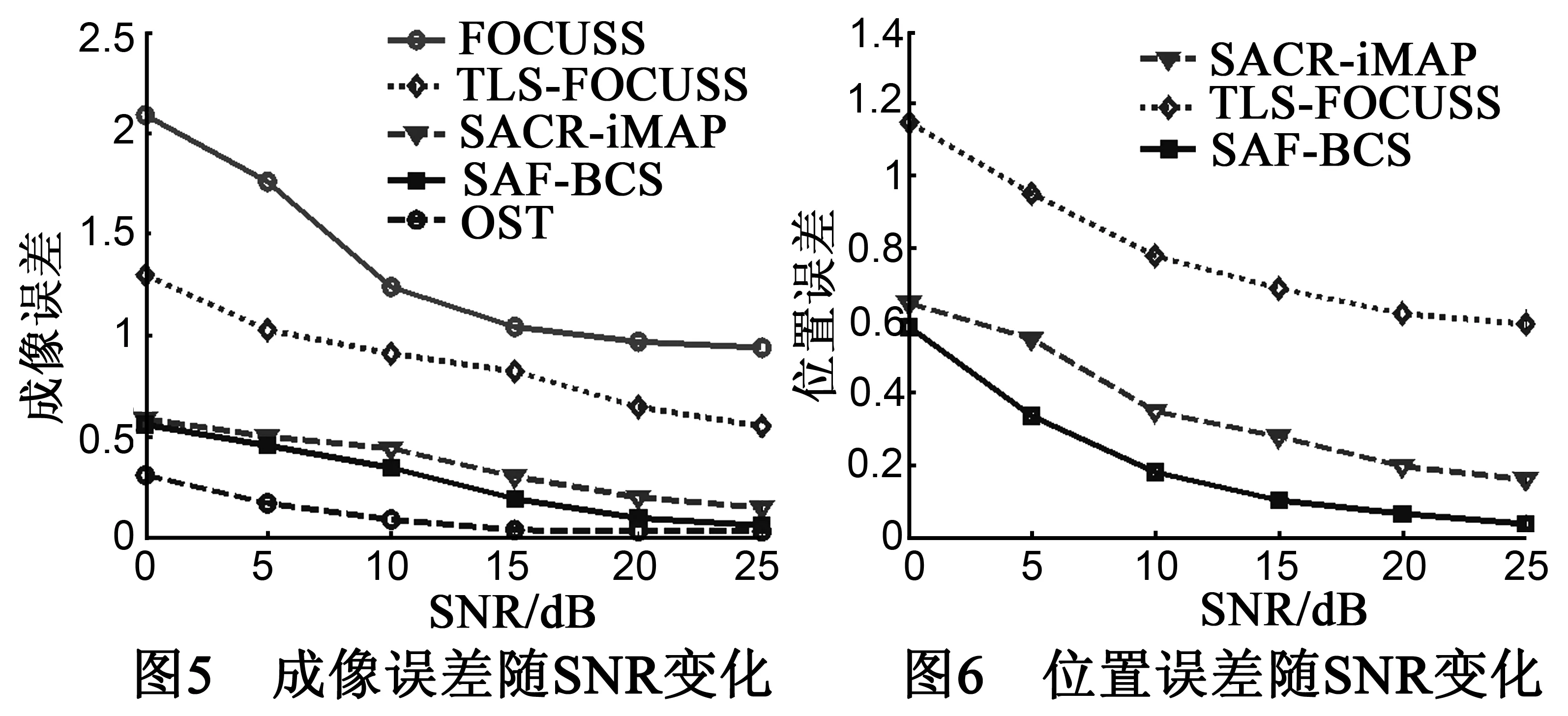
为了衡量不同稀疏方法的重构性能，这里增加OSR(Oracle Sparse Recovery[14])算法，即预先精确已知目标散射点位置，直接利用最小二乘方法求解散射系数.假设SNR从0dB至25dB变化，成像区域、目标模型与实验1一致，图5～图6为不同方法的成像误差和位置误差随SNR变化的关系曲线.由图5可见，SAF-BCS的成像误差均低于其他方法，且随着SNR增大其成像性能逐渐逼近OSR.由图6可以看出SAF-BCS的位置误差估计结果亦是最小的.

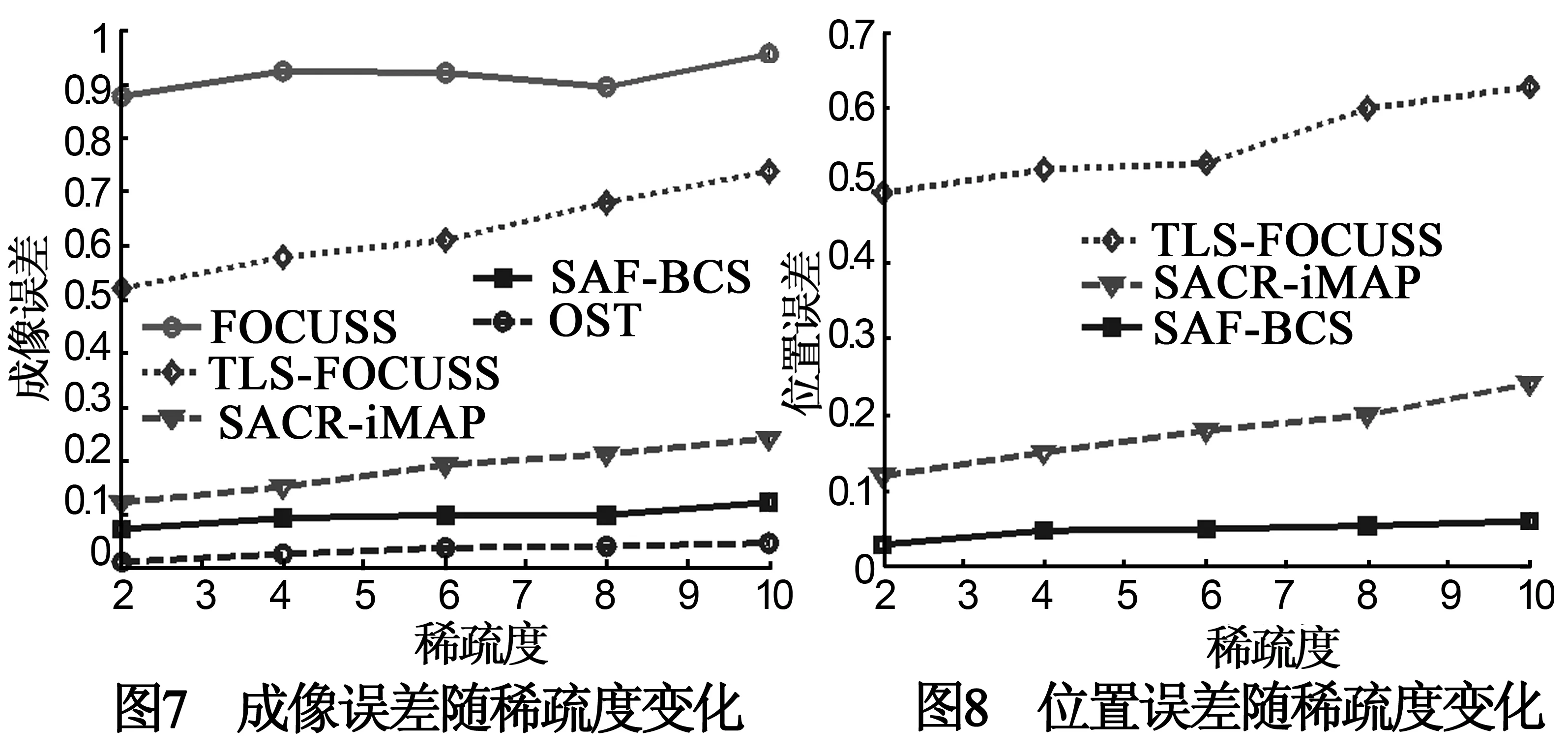
图7、8为不同方法的成像误差和位置误差随稀疏度(散射点数目)变化的关系曲线.这里成像区域、网格划分大小与实验1一致，SNR=20dB.可以看出，随着稀疏度的增大，这些方法在迭代更新寻找散射点位置信息时出错机率都有一定程度的增加，成像误差也随之增大.但相比而言，SAF-BCS具有最好的成像效果.

5　结论

针对FD-MIMO雷达应用传统CS成像算法时存在网格失配问题，本文提出了一种基于贝叶斯压缩感知的稀疏自聚焦成像(SAF-BCS)算法.与已有稀疏重构方法相比，SAF-BCS对网格划分不敏感，具有稳健的目标信息提取能力，并且可以应用至其他Off-grid问题的求解，如ISAR成像、DOA等.

[1]D Tarchi,F Oliveri,P F Sammartino.MIMO radar and ground-based SAR imaging systems:equivalent approaches for remote sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(1):425-435.

[2]Liu Chang-chang,Chen Wei-dong.Sparse frequency diverse MIMO radar imaging[A].Preceedings of the 46th Asilomar Conference on Signals,Systems and Computers[C].California,USA:IEEE,2012.853-857.

[3]徐刚,张磊,陈倩倩,等.基于稀疏约束最优化的ISAR 相位自聚焦成像算法[J].电子学报,2013,41(9):1772-1777.

Xu Gang,Zhang Lei,Chen Qian-qian,et al.Novel autofocusing algorithm for ISAR imaging based on sparse constraint[J].Acta Electronica Sinica,2013,41(9):1772-1777.(in Chinese)

[4]Eender J.A brief review of compressive sensing applied to radar[A].Preceedings of the IEEE International Radar Symposium (IRS)[C].Dresden,Germany:IEEE,2013.3-16.

[5]Tan Xin,W Roberts,Li Jian,et al.Sparse learning via iterative minimization with application to MIMO radar imaging[J].IEEE Transactions on Signal Processing,2011,59(3):1088-1101.

[6]M Duman,A C Gurbuz.Analysis of compressive sensing based through the wall imaging[A].Preceedings of the IEEE Radar Conference[C].Atlanta,USA:IEEE,2012.0641-0646.

[7]Wang Tian-yun,Liu Chang-chang,Lu Hong-chao,et al.Sparse passive radar imaging based on digital video broadcasting satellites using the MUSIC algorithm[A].Preceedings of the IEEE 11th International Conference on Signal Processing (ICSP)[C].Beijing,China:IEEE,2012.1925-1930.

[8]S Ugur,O Arikan,A C Gurbuz.Off-grid sparse SAR image reconstruction by EMMP algorithm[A].Preceedings of the IEEE Radar Conference[C].Ottawa,Canada:IEEE,2013.1-4.

[9]Wang Tian-yun,Lu Xin-fei,Yu Xiao-fei,et al.A fast and accurate sparse continuous signal reconstruction by homotopy DCD with nonconvex regularization[J].Sensors,2014,14(4):5929-5951.

[10]E Candes,J Romberg.Sparsity and incoherence in compressive sampling[J].Inverse Problems,2007,23(3),969-985.

[11]王超宇,贺亚鹏,朱晓华,等.基于贝叶斯压缩感知的噪声 MIMO 雷达稳健目标参数提取方法[J].电子与信息学报,2013,35(10):2498-2504.

Wang Chao-yu,He Ya-peng,Zhu Xiao-hua,et al.A robust target parameter extraction method via Bayesian compressive sensing for noise MIMO radar[J].Jounal of Electronics & Information Technology,2013,35(10):2498-2504.(in Chinese)

[12]Han Xue-bing,Zhang Hao,Li Gang.Fast algorithms for sparse recovery with perturbed dictionary[EB/OL].http://arxiv.org/pdf/1111.6237.pdf,2012.5.

[13]Yang Zai,Xie Li-hua,Zhang Ci-shen.Off-grid direction of arrival estimation using sparse Bayesian inference[J].IEEE Transactions on Signal Processing,2013,61(1):38-43.

[14]He Xue-zhi,Liu Chang-chang,Liu Bo,et al.Sparse frequency diverse MIMO radar imaging for off-grid target based on adaptive iterative MAP[J].Remote Sensing,2013,5(2),631-647.

[15]S D Babacan,R Molina,A K Katsaggelos.Bayesian compressive sensing using Laplace priors[J].IEEE Transactions on Image Processing,2010,19(1):53-63.

[16]D G Tzikas,C L Likas,N P Galatsanos.The variational approximation for Bayesian inference[J].IEEE Signal Processing Magazine,2008,25(6):131-146.

[17]保铮,邢孟道,王彤.雷达成像技术[M].北京：电子工业出版社,2010.24-30.

[18]Liu Hong-chao,Jiu Bo,Liu Hong-wei,et al.Superresolution ISAR imaging based on sparse Bayesian learning[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(8):5005-5013.

[19]A J Lemonte,G M Cordeiro.The exponentiated generalized inverse Gaussian distribution[J].Statistics & Probability Letters,2011,81(4):506-517.

[20]CVX Research,Inc.CVX:Matlab software for disciplined convex programming[EB/OL].http://cvxr.com/cvx/,2014.6.

王天云男，1986年出生于河南信阳，中国科学技术大学在读博士研究生，研究方向为分布式雷达稀疏成像、压缩感知技术等.

E-mail：wangty@mail.ustc.edu.cn

陆新飞男，1990年出生于安徽亳州，为中国科学技术大学在读博士研究生，研究方向为高分辨雷达成像、阵列信号处理技术等.

丁丽女，1985年出生于浙江安吉，2014年获中国科学技术大学博士学位，现为上海理工大学讲师，研究方向为MIMO雷达成像、太赫兹成像技术等.

尹治平男，1980年出生于湖北常宁，合肥工业大学副研究员，硕士生导师，研究方向为雷达与微波成像.

陈卫东(通信作者)男，1968年生于安徽合肥，中国科学技术大学教授，博士生导师，研究方向为雷达系统理论与技术、雷达信号处理、微波与毫米波技术.

E-mail：wdchen@ustc.edu.cn

Bayesian Compressive Sensing-Based Sparse Imaging for Off-Grid Target in Frequency Diverse MIMO Radar

WANG Tian-yun1,2,LU Xin-fei2,DING Li2,YIN Zhi-pin3,CHEN Wei-dong2

(1.ChinaSatelliteMaritimeTrackingandControlDepartment,Jiangyin,Jiangsu214431,China;2.KeyLaboratoryofElectromagneticSpaceInformation,ChineseAcademyofSciences,UniversityofScienceandTechnologyofChina,Hefei,Anhui230027,China;3.AcademyofPhotoelectricTechnology,HefeiUniversityofTechnology,Hefei,Anhui230009,China)

Conventional compressive sensing (CS) imaging methods rely on the assumption that all scatterers in the imaging scene are located exactly on the pre-defined grids.However,since the scatterers are distributed in a continuous scene,the off-grid problem inevitably exists,which makes basis mismatch between echo measurement and the assumed sensing matrix,and leads to considerable performance degradation by CS-based methods.Therefore,this paper investigates the sparse imaging for off-grid target in frequency diverse multiple-input multiple-output (FD-MIMO) radar.A sparse autofocus imaging method based on Bayesian compressive sensing (SAF-BCS) is proposed.It employs the technique of variational Bayesian inference to achieve the imaging of off-grid scatterres in light of the criterion of maximum a posteriori (MAP).Compared with the conventional sparse recovery algorithms,the proposed method adequately utilizing the prior information of the target,is able to automatically tune parameters,and thus can provide a better capability to correct the off-grid errors,and to estimate the noise power,etc.Simulation results confirm that SAF-BCS is not sensitive to grid discretization,and has a robust imaging performance.

Bayesian compressive sensing;FD-MIMO radar;off-grid target;variational Bayesian inference;sparse autofocus imaging

2014-08-30;修回日期:2015-02-04;责任编辑:梅志强

国家自然科学基金(No.61172155,No.61401140，No.61403421)；国家863计划项目资助课题(No.2013AA122903)

TN958

A

0372-2112 (2016)06-1314-08