目标海拔已知的信号到达幅度比无源定位方法

曹景敏,万　群,魏合文,刘郁林

(1.电子科技大学电子工程学院,四川成都 611731;2.西南电子电信技术研究所,四川成都610041;3.总参通信工程设计研究院,辽宁沈阳 110005)



目标海拔已知的信号到达幅度比无源定位方法

曹景敏1,2,万群1,魏合文2,刘郁林3

(1.电子科技大学电子工程学院,四川成都 611731;2.西南电子电信技术研究所,四川成都610041;3.总参通信工程设计研究院,辽宁沈阳 110005)

信号到达幅度比方法因测量简便,可实现对窄带信号的无源定位而广泛应用于射频定位系统、无线传感器网络和声源定位中.当目标海拔已知,将其作为定位方程的约束条件可实现对目标更精确的定位,而现有方法没有考虑这个问题.对此本文建立了海拔约束的信号到达幅度比无源定位模型,推导了定位精度的克拉美劳下界,并提出了一种基于Newton迭代的定位算法.理论推导表明该算法在测量误差服从方差较小的零均值高斯分布时能够达到克拉美劳下界,仿真结果与理论推导一致.无线电栅格化监测试验网的验证结果表明,对系统幅度误差进行校正后,该方法能够实现对辐射源的准确定位.

信号到达幅度比;无源定位;海拔约束;克拉美劳下界;Newton迭代

1　引言

基于信号幅度信息的定位方法在基于射频的定位系统[1],无线传感器网络[2～4],声音信号源定位[5～8]中有广泛应用.基于信号到达幅度信息的定位方法利用多个传感器接收到的信号幅度信息实现对辐射源的定位.常用的基于幅度信息的定位方法包括接收信号强度RSS(Receive Signal Strength)定位方法[1～8]和接收信号到达幅度比GROA定位方法[9～13].

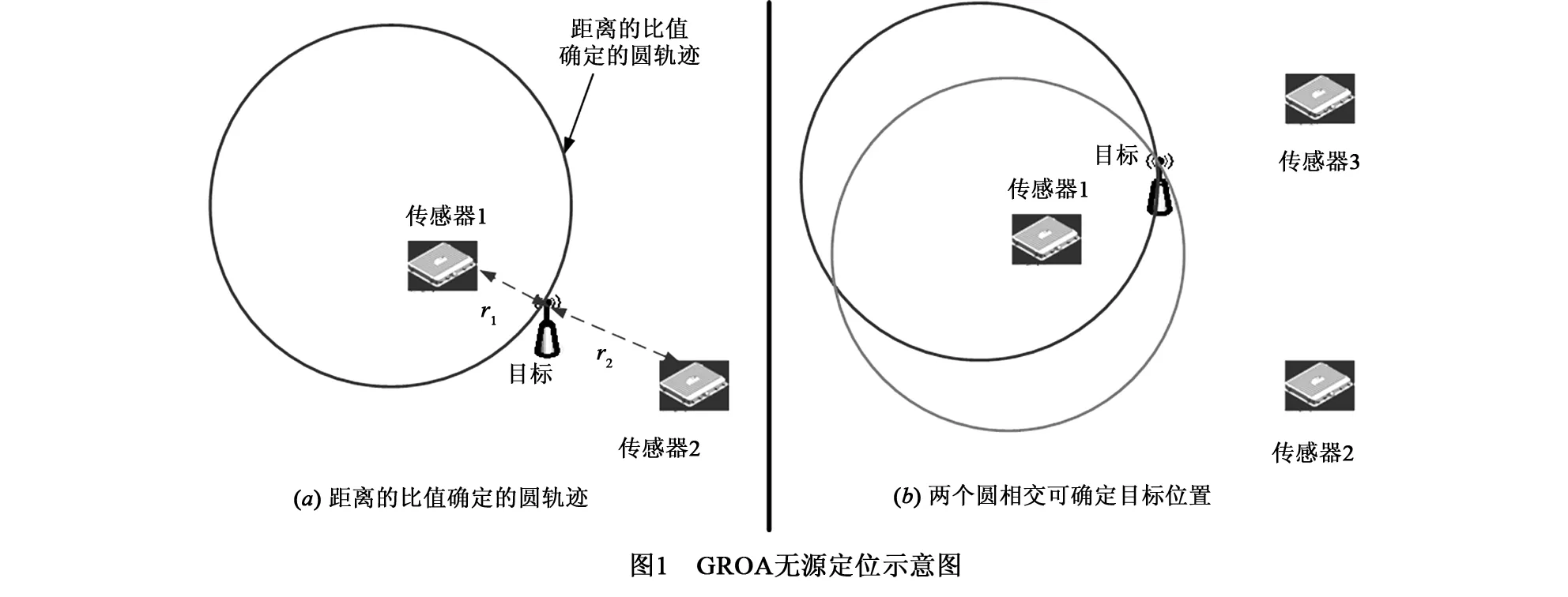
GROA定位方法是利用自由空间传播时接收信号的幅度与传播距离成反比[9]的原理来对目标进行定位的.图1所示为GROA定位方法的示意图,图1(a)所示为利用信号到达两个传感器的距离比值确定二维平面内的一个圆,图1(b)所示为利用三个传感器获得的圆轨迹相交确定目标位置.

GROA定位方法相对于AOA(Angle of Arrival),TDOA(Time Difference of Arrival),RSS等定位方法的优点包括:(1)GROA定位是利用信号的幅度信息进行定位,信号幅度信息自然包括在接收信号中,所以相比于需要利用阵列的AOA定位方法和需要时间同步的TDOA定位方法,实现GROA定位更廉价.(2)RSS定位方法也是一种利用幅度信息的定位方法,但RSS定位方法需要事先已知待定位目标的信号发射功率和信号传播的路径损耗模型,因此不适用于无源被动定位,利用GROA的方法不需要此类先验信息,适用于无源定位.(3)TDOA参数估计精度的克拉美劳下界与信号带宽的三次方成反比,所以TDOA定位方法对于带宽很小信号的定位精度很低.而GROA定位方法对带宽很小的信号有优势,在TDOA和GROA混合的定位中,随着信号带宽的减小,GROA对定位精度的改善起到了关键的作用[9].所以,GROA定位方法可以成为TDOA定位方法的一种补充,实现对带宽很小信号的定位.

GROA的定位方法首先由K.C.Ho等人在文献[9]中提出.他们提出同时利用GROA和TDOA的两步WLS(Weighted Least Square)无源定位方法.文献[9]指出在这两种混合的定位方法中,随着信号带宽的减小,GROA对定位精度的改善起到了关键的作用.在此基础上文献[10]提出了在传感器位置有误差条件下的多个目标定位的RDOA (Range Difference of Arrival)和GROA混合定位方法,文献[11]将AOA信息加入到GROA和TDOA的混合定位中来,推导了AOA-GROA-TDOA定位的CRLB.在较低信噪比条件下,文献[9]中的两步WLS定位算法性能不佳,而文献[12]中提出的准牛顿(quasi-Newton)迭代方法在信噪比较低条件下精度优势明显.文献[13]在文献[9]基础上,提出了改进定位偏差的方法.然而,以上GROA定位方法都没有考虑实际地球目标定位中的目标海拔已知时的定位.

在实际地球目标定位中,当增加目标海拔信息,可以提高GROA定位方法的适用性和精确性:当传感器数量为3时,无法进行GROA定位,增加目标海拔信息时可进行三站海拔约束的GROA定位;当传感器数量大于3时,增加目标海拔信息,可以提高GROA无源定位方法的精度.在某些实际应用中,可以获得目标海拔先验信息或可以根据目标的属性对目标海拔进行合理假设,在此条件下,可以采用目标海拔已知的GROA无源定位方法.一些典型目标的海拔范围,执勤时的典型海拔如表1所示.

文献[14]把海拔约束引入到基于TDOA的定位方法中,获得了定位精度的提升.受文献[14]启发,本文针对目标海拔信息已知应用,研究目标海拔已知条件下的GROA无源定位方法.目标海拔已知条件下的GROA定位方法需要解决目标海拔的约束关系问题,并且需要充分考虑辐射源位置坐标与测量参数之间的非线性关系.本文提出的新方法把海拔约束作为最小化目标函数中的一个约束条件,而针对辐射源位置与测量参数之间的非线性关系,通过引入一个中间变量,将非线性观测方程变成线性化观测方程,同时又充分考虑到这一中间变量与目标位置之间的函数关系来对目标进行定位解算.

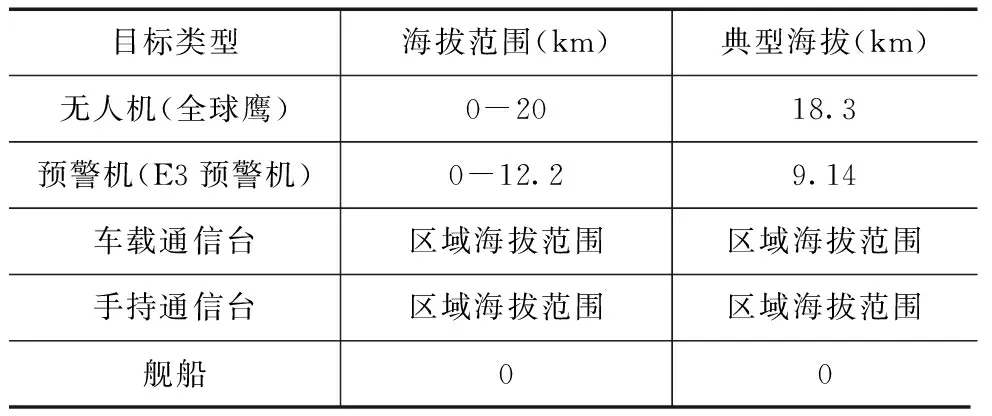
表1　一些典型目标执勤情况下的海拔

2　目标海拔已知的GROA定位模型

2.1定位模型

在大地坐标系中,假设第i个传感器位置为[Ei,Ni,Hi]T,(i=1,2,…,M),其中Ei、Ni和Hi分别表示第i个传感器的经度、纬度和海拔.目标的坐标为[Es,Ns,h]T,其中目标海拔h已知,精度Es和纬度Ns待求.若将地球看成球体,通过坐标转换,可将大地坐标转换成以地球球心为原点的三维直角坐标.转换后的第i个传感器位置坐标假设为si=[xi,yi,zi]T,(i=1,2,…,M),目标位置坐标为u=[xs,ys,zs]T.根据接收信号幅度与电磁波传播距离成反比的关系[9],以第1个传感器为参考,GROA参数可写成:

gi1=ri/r1,(i=2,3,…,M)

(1)

其中ri,r1分别表示目标到第i个和第1个传感器的距离:

(2)

为方便表示,GROA参数写成向量形式为:

g=[g21,g31,…,gM1]T

(3)

当目标海拔h已知时有:

uTu=(Re+h)2

(4)

其中Re为地球半径.

由式(1)～(4),海拔约束下的GROA定位方法可建模为:

(5)

上式方程组中,第一个方程为幅度比方程,第二个方程为海拔约束方程.

2.2定位精度的理论下界

在统计信号处理的估计理论中,无偏估计量的方差存在理论下界.理论下界可以作为评价各种算法好坏的一个标准,并且可以提醒我们不可能找到一种超出这种理论下界的算法.在无偏估计问题中常用的是CRLB.参考已知目标海拔条件下TDOA定位的CRLB结论[14],下面给出已知目标海拔条件下的GROA定位模型的CRLB.

把g写成g=g0+Δg,g0为真实值分量,假设Δg服从零均值高斯分布时[9]:

E(Δg)=0

(6a)

E(ΔgΔgT)=Qt

(6b)

其中Qt为幅度比参数测量误差的协方差矩阵.

无约束GROA定位方法的CRLB为:

(7)

其中J为Fisher信息矩阵:

(8)

其中

(9)

已知目标海拔的GROA无源定位方法的CRLB可表示为:

B2=J-1-J-1F(FTJ-1F)-1FTJ-1|u=u0

(10)

其中F为约束方程的梯度矩阵:

F=2u

(11)

式(10)等号右端第一项J-1为无海拔约束条件的CRLB,第二项-J-1F(FTJ-1F)-1FTJ-1由约束方程引起.

3　目标海拔已知的GROA无源定位算法

3.1目标海拔已知的GROA定位算法

将式(2)中的第一个等式两边平方并写成矩阵形式为:

(12)

利用式(1),式(12)可写为:

(13)

式(13)写成矩阵形式为:

(14)

其中

(15)

(16)

(17)

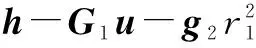
(18)

其中W为加权矩阵:

(19)

其中αt是由GROA参数测量误差引起的方程误差向量:

(20)

用噪声分量表示时,式(20)可写成:

(21)

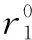
αt=-Δg2

(22)

在目标海拔约束条件下,海拔约束方程uTu=(Re+h)2作为目标函数的约束条件,同时考虑到中间变量r1与目标位置u之间的函数关系,即式(12)的等式关系,可得有两个约束条件的最小化目标函数:

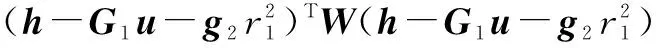
+λ2(uTu-(Re+h)2)

(23)

其中λ1、λ2为约束系数.使ξ最小值的u值即为目标位置的估计值.

求解ξ的最小值需要对未知量u和r1分别求导,令导数值为零可得:

(24)

和

(25)

其中

(26)

(27)

(28)

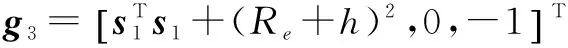
(29)

其中

(30)

把式(29)代入(24)有:

u=G7r1

(31)

其中

(32)

把式(29)和(31)代入(25)得:

g8r1=0

(33)

其中

(34)

在式(33)中,对于一个特定λ2,通常只对应一个正的r1,把此r1代入(32)可得到λ2与目标位置的关系式.再利用式(4)可得到目标位置的解.Newton迭代方法可以用于求解ρ(λ2)=uTu-(Re+h)2方程.由于λ2=0是没有海拔约束的解,Newton迭代时的λ2初始值可设为零.

3.2算法性能分析

下面利用扰动法分析已知目标海拔条件下GROA算法的定位性能.把幅度比测量参数g2表示成:

(35)

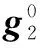
为方便表示,r1、u也写成式(35)形式:

(36)

u=u0+Δu

(37)

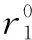
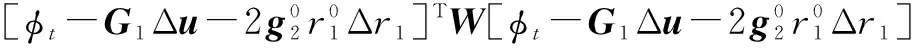
(38)

令ξ对Δu、Δr1、λ1和λ2的导数为零可得:

(39)

(40)

(41)

(u0)TΔu=0

(42)

把式(41)代入式(40)得:

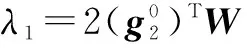
(43)

其中

(44)

把式(41)和式(43)代入式(39)得:

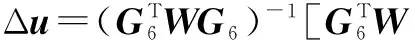
(45)

上式两边左乘(u0)T并利用式(42)得:

(46)

把式(46)代入式(45)有:

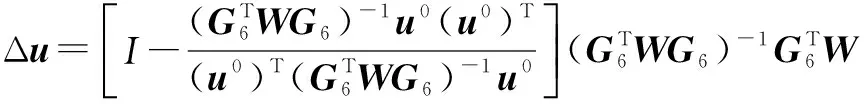
(47)

由

E(φt)=E(-Δg2)=0

(48)

有

E(Δu)=0

(49)

因此,本文提出的对u的估计是一种无偏估计,且有:

(50)

显然:

cov(u)u0=0

(51)

即目标位置估计的协方差与目标真实位置正交.将式(50)写成:

(52)

对比式(10)和式(52)不难证明

cov(u)=B2

(53)

上式表明,已知目标海拔条件下的GROA定位算法在幅度比参数为方差很小的零均值高斯噪声时能够达到定位误差的理论下界,是一种渐近最优算法.

4　仿真分析

仿真中假设单个目标静止不动,大地坐标系坐标为[104.0381°E,30.6650°N,500m],8个定位传感器坐标如表2所示.

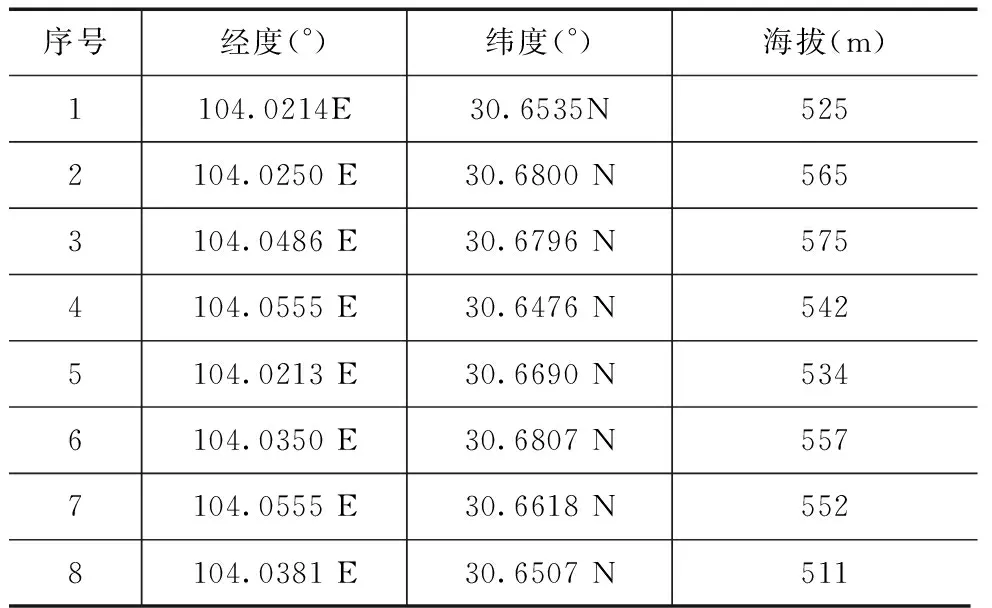
表2　定位传感器大地坐标系坐标

在目标海拔已知条件下,定位的CRLB与本文定位算法随测量参数方差的变化曲线如图2所示,结果为1000次独立实验的平均值,假设幅度比参数测量误差为零均值的高斯白噪声,定位传感器为序号1～6的传感器.从图2可看出,随着参数测量误差的减小,定位算法的均方根误差也减小,并且越来越接近CRLB.

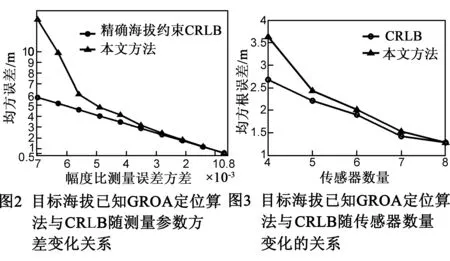
图3为在目标海拔已知条件下,本文提出的GROA定位算法与CRLB随传感器数量变化的曲线图.其中,GROA参数误差为零均值的高斯白噪声,噪声方差为0.002,结果为1000次统计的平均值.图3表明,定位算法的均方根误差随着传感器数量增多而减小,并且越来越接近CRLB.

计算无海拔约束CRLB[9]和准确海拔约束条件下的CRLB,传感器数量分别为4和8时的结果如图4所示.从图4看出,目标海拔已知CRLB比无海拔约束时的CRLB低了45dB左右,这由式(10)中等号右边第二项-J-1F(FTJ-1F)-1FTJ-1的精确海拔约束引起.

在实际应用过程中,当非合作目标的海拔未知时,可以对目标海拔进行合理的假设.假设的目标海拔往往存在误差.当GROA参数误差为零均值的高斯白噪声,利用1～8号传感器进行定位,进行1000次的统计平均,本文提出的海拔约束的GROA定位方法在把目标海拔分别约束为550m,750m即海拔约束误差分别为50m和250m时的GROA定位误差如图5所示.当没有TDOA测量时,KCHo方法[9]可以退化成基于两步WLS的无约束GROA定位算法,该方法的定位均方根误差曲线与相应的CRLB如图5所示.

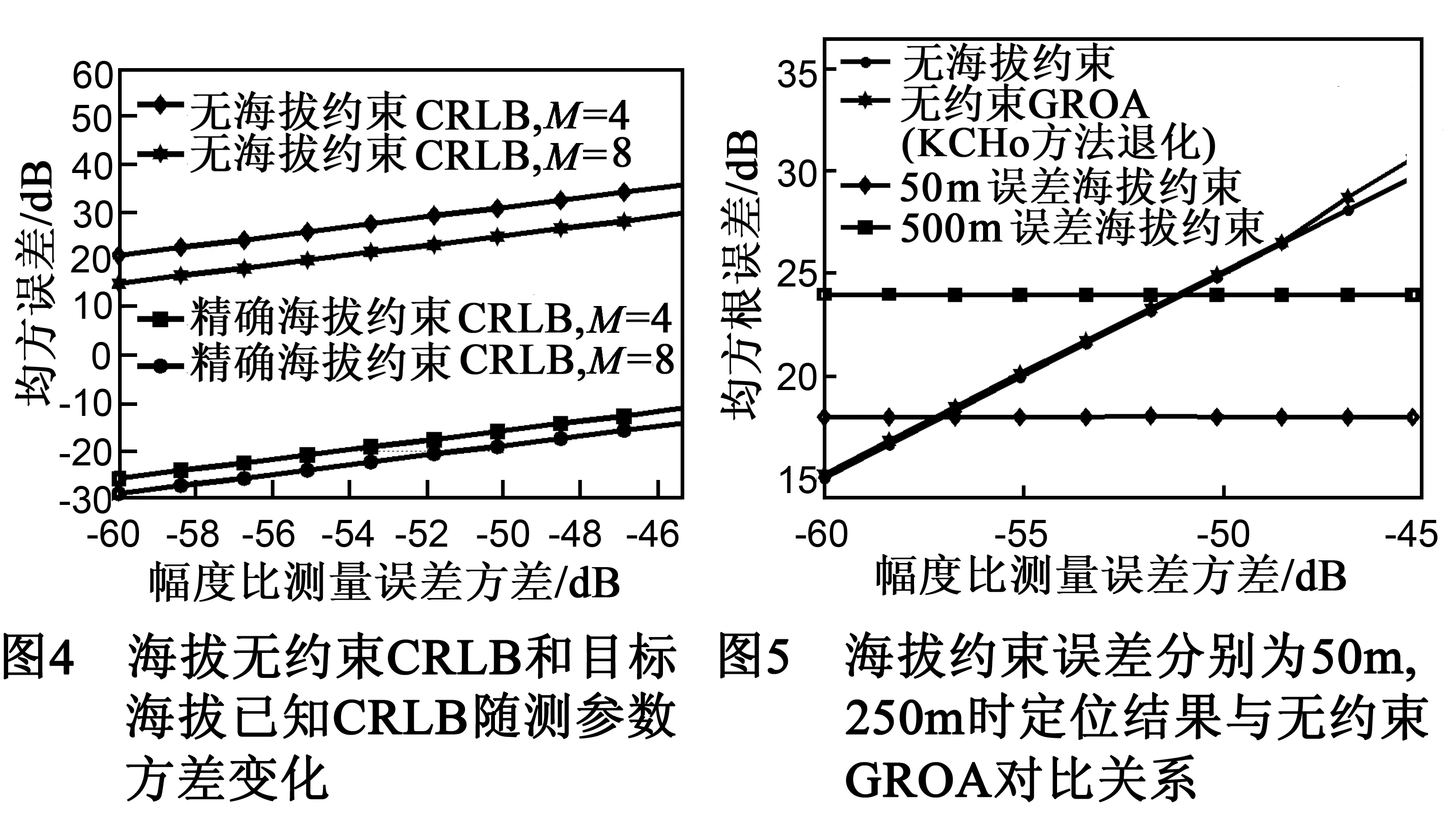
从仿真结果可以看出,对于无约束GROA定位而言,由KCHo方法退化的定位方法在小高斯噪声条件下很接近CRLB.对于约束GROA定位而言,在测量误差方差很小时,如果约束误差不变,则定位误差基本保持不变.这是因为在测量误差方差很小时,定位误差主要由约束误差引起,当约束误差不变时其定位误差基本不变.对比无约束GROA定位与有海拔约束误差的GROA定位的结果可发现,幅度比测量误差和海拔约束误差影响可等效于无约束定位方法中一定的幅度比测量误差影响,当测量误差方差小于等效误差值时用无约束定位方法精度更高,当测量误差方差大于等效误差值时海拔约束定位方法精度更高.

5　实测结果分析

利用在成都市中心和西二环之间建立的无线电栅格化监测试验网,开展了海拔约束的GROA无源定位方法的试验验证.试验网共有8个信号采集点,覆盖频段为30～3000MHz,传感器基线长为1.8～2.5km,覆盖区域范围约为10km2.

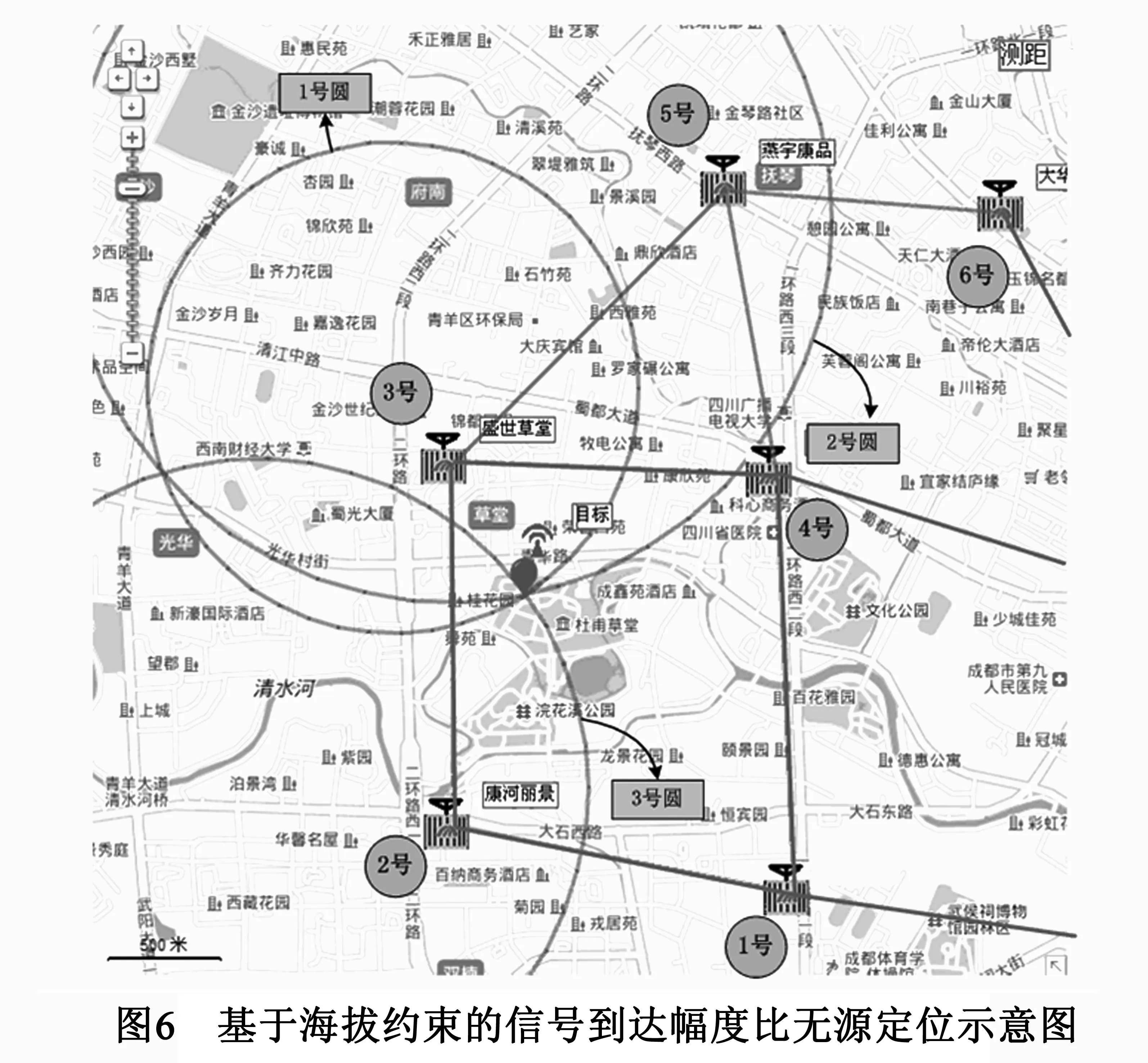
图6所示为2013年11月18日的试验结果.控制信号源发射载频为325MHz,带宽为10kHz的PSK信号.2、3和4号传感器点收到信号,利用这3个点接收到信号计算信号到达幅度比值(信号幅度值由信号能量开方获得),加上发射点的海拔约束可进行信号定位.其中发射点海拔高度为565m.定位中选择3号传感器为参考传感器.图中所示的1号圆为4号传感器与3号传感器接收信号的幅度比值确定的圆,2号圆为2号传感器与3号传感器接收信号的幅度比的值确定的圆,3号圆为将2、4号传感器与3号传感器的信号到达幅度比值相除得到的值确定的圆.图中实心椭圆为定位点,其与信号源真实位置距离误差为237m.

需要特别说明的是,在试验中,影响接收信号幅度比值测量精度的影响因素有很多,主要包括电磁波传播的各向异性影响,接收天线的增益不一致,接收天线到电缆的长度不一致,接收机增益不一致等.接收天线的增益,接收天线到电缆的长度,接收机增益的不一致可以通过补偿校正来减小影响.而电磁波传播的各向异性受电波传播环境影响,表现为时变特性.图6中的结果就是在对以上影响因素实时统一校正后的定位结果.

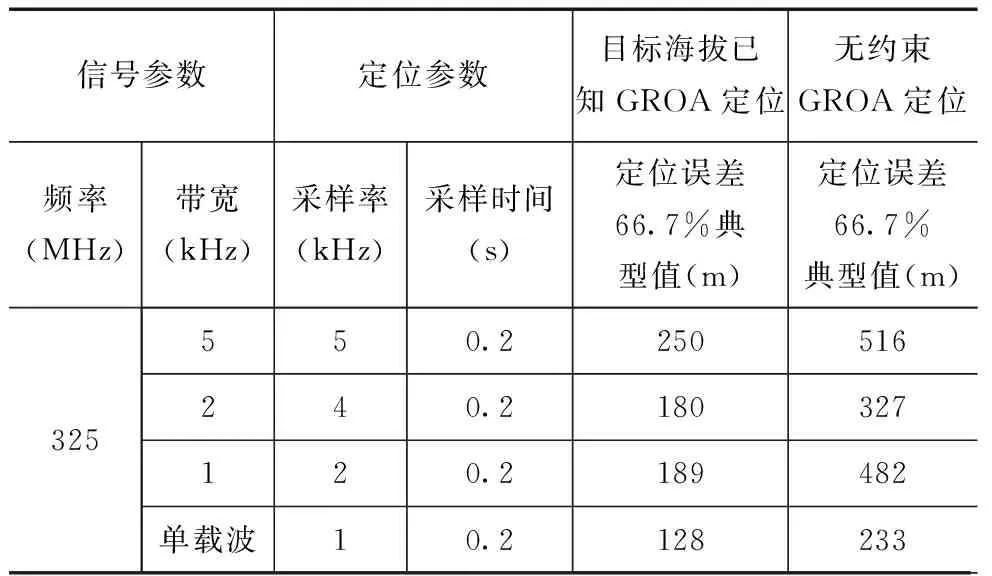
表3目标海拔已知GROA定位和无约束GROA定位实测统计结果

信号参数定位参数目标海拔已知GROA定位无约束GROA定位频率(MHz)带宽(kHz)采样率(kHz)采样时间(s)定位误差66.7%典型值(m)定位误差66.7%典型值(m)325550.2250516240.2180327120.2189482单载波10.2128233

在同一时间段内,利用校正后的系统进行多次测量统计,载频为325MHz,带宽分别为5kHz,2kHz,1kHz和单载波时的定位统计结果如表3.根据传感器测量的幅度比参数,利用Matlab实现的无约束GROA定位算法计算定位误差,统计结果如表3中所示.其中定位误差66.7%典型值表示66.7%的定位误差小于等于该典型值.统计的次数为100次.

试验的结果表明,在对系统幅度误差进行有效校正后,基于海拔约束的信号到达幅度比无源定位方法能够实现对辐射源的有效定位.该定位方法的定位精度与信号的带宽有关系,带宽越小定位精度越高.这与幅度比定位参数的估计精度有关,当信号带宽较宽时,带内噪声分量较多,影响了幅度比参数的估计精度.对比目标海拔已知GROA定位和无约束GROA定位结果发现,相同条件下,当引入精确目标海拔高度时,目标海拔已知的GROA定位精度比无约束GROA定位精度更高.

6　结论

目标海拔已知时,通过增加目标海拔约束方程可以获得目标海拔已知的GROA无源定位模型和定位算法.目标海拔已知的GROA无源定位算法通过构造带约束的最小化目标函数实现对目标位置的估计求解,该算法在测量误差服从方差较小的零均值高斯分布时能够达到CRLB,是一种渐近最优算法,仿真结果验证了算法的最优性能.当海拔约束有误差时,海拔约束GROA定位的幅度比测量误差和海拔约束误差影响可等效于无约束GROA定位方法中一定的幅度比测量误差影响,当测量误差方差大于等效误差值时,用海拔约束GROA定位方法精度更高.基于无线电栅格化监测试验网的实测结果表明,在对系统幅度误差进行有效校正后,基于海拔约束的GROA定位方法能够实现对辐射源的有效定位,其精度高于无约束GROA定位方法,并且信号带宽较小,定位精度越高.

[1]P BAHL,V N PADMANABHAN.RADAR:An in-building RF-based user location and tracking system[A].INFOCOM 2000 Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies[C].Tel Aviv,Israel:IEEE,2000.775-784.

[2]MOHAMMAND R G,REZA M V,ERIK G S.RSS-based sensor localization in the presence of unknown channel parameters[J].IEEE Transactions on Signal Processing,2013,61(15):3752-3759.

[3]REZA M V,MOHAMMAD R G,R M BUEHRER,et al.Cooperative received signal strength-based sensor localization with unknown transmit powers[J].IEEE Transactions on Signal Processing,2013,61(6):1389-1403.

[4]ANGELO C.Reduced-bias ML-based estimators with low complexity for self-calibrating RSS ranging[J].IEEE Transactions on Wireless Communications,2013,12(3):1220-1230.

[5]LI D,HU Y-H.Least square solution of energy based acoustic source localization problems[A].2004 International Conference on Parallel Processing Workshops[C].Montreal,QC,Canada:IEEE,2004.443-446.

[6]S T BIRCHFIELD,R GANGISHETTY.Acoustic localization by intermural level difference[A].2005 IEEE International Conference on Acoustics,Speech,Signal Processing[C].Philadelphia,USA:IEEE,2005.1109-1112.

[7]SHENG X,HU Y-H.Maximum likelihood multiple-source localization using acoustic energy measurements with wireless sensor networks[J].IEEE Transactions on Signal Processing,2005,53(1):44-53.

[8]K C HO,SUN Ming.An accurate algebraic closed-form solution for energy-based source localization[J].IEEE Transactions on Audio,Speech and Language Processing,2007,15(8):2542-2550.

[9]K C Ho,SUN Ming.Passive source localization using time differences of arrival and gain ratios of arrival[J].IEEE Transactions on Signal Processing,2008,56(2):464-477.

[10]HAO Ben-jian,LI Zan,REN Yun-mei,et al.On the Cramer-Rao bound of multiple sources localization using RDOAs and GROAs in the presence of sensor location uncertainties[A].2012 IEEE Wireless Communications and Networking Conference Mobile and Wireless Networks[C].Shanghai,China:IEEE,2012.3117-3122.

[11]LUO Ji-an,ZHANG Xiao-ping,WANG Zhi.A new passive source localization method using AOA-GROA-TDOA in wireless sensor array networks and its Cramer-Rao bound analysis[A].2013 IEEE International Conference on Acoustics,Speech and Signal Processing[C].Vancouver,BC,Canada:IEEE,2013.4031-4035.

[12]HAO Ben-jian,LI Zan,BFGS quasi-Newton location algorithm using TDOAs and GROAs[J].Journal of Systems Engineering and Electronics,2013,24(3):341-348.

[13]HAO Ben-jian,LI Zan,QI Pei-han,et al.Effective bias reduction methods for passive source localization using TDOA and GROA[J].Science China-Information Sciences,2013,56(7):1-12.

[14]K C HO,Y T CHAN.Geo-location of a known altitude object from TDOA and FDOA measurements[J].IEEE Transactions on Aerospace and Electronic Systems,1997,33(3):770-783.

[15]XU Zhen,WANG Jing.Source localization by collaborating multiple measurements with inaccurate sensor positions[A].2011 8th International Conference on Information,Communications and Signal Processing[C].Singapore:IEEE,2011.1-5.

[16]N PATWARI,J N ASH,S KYPEROUNTSA,et al.Locating the nodes:cooperative localization in wireless sensor networks[J].IEEE Signal Processing Magazine,2005,22(4),54-69.

[17]S M Kay.Fundamentals of Statistical Signal Processing:Estimation Theory[M].Englewood Cliffs NJ:Prentice-Hall,1993.23-70.

曹景敏男,1987年10生于福建龙岩.现为电子科技大学电子工程学院博士研究生.主要研究方向为目标定位与跟踪.

E-mail:caojjmail@163.com

万群 男,1971年生于江西南昌.现为电子科技大学教授、博士生导师.主要研究方向为阵列信号处理、雷达信号处理,目标定位跟踪.

E-mail:wanqun@uestc.edu.cn

Passive Location of a Known Altitude Object Using Gain Ratio of Arrival Measurements

CAO Jing-min1,2,WAN Qun1,WEI He-wen2,LIU Yu-lin3

(1.DepartmentofElectronicEngineering,UniversityofElectronicScienceandTechnologyofChina,Chengdu,Sichuan611731,China;2.ChinaSoutheastElectronicTelecomTechnologyResearchInstitute,Chengdu,Sichuan610041,China;3.InstituteofCommunicationsEngineeringDesignoftheGeneralStaff,Shenyang,Liaoning110005,China)

The localization methods based on signal amplitude are widely used in radio frequency based location system,wireless sensor network and acoustic location system.The conventional gain ratios of arrival (GROA) passive localization methods take no consideration of the altitude of the source,though it is usually known.A GROA model with known altitude of the source was proposed,and the Cramer-Rao low bound (CRLB) was also derived.And then,a localization algorithm based on Newton iteration was proposed and it was proved theoretically to reach the CRLB under the Gaussian noise data model.The simulations validated the theoretical conclusions.This algorithm was also verified in a wireless monitoring network.In conclusion,this algorithm can accurately localize the source with known altitude.

GROA;passive localization;known altitude;CRLB;Newton iteration

2014-11-20;修回日期:2015-02-15;责任编辑:覃怀银

国家自然科学基金(No.61172140,No.61401069);重庆高校创新团队建设计划(No.KJTD201343);教育部“新世纪优秀人才支持计划”(No.NCEF-11-0873)

TN97

A

0372-2112 (2016)06-1369-07