基于多参数延时决策的低重频雷达速度估计方法研究
2016-08-12周万幸
周万幸
(南京电子技术研究所,江苏南京 210039)
基于多参数延时决策的低重频雷达速度估计方法研究
周万幸
(南京电子技术研究所,江苏南京 210039)
航迹滤波中引入速度量测可提高滤波精度,但低重频雷达测速存在模糊,针对距离微分或Kalman滤波速度估计精度不能完全满足低重频测速解模糊问题,提出了多参数延时决策方法的速度模糊滤波方法.该方法以贝叶斯航迹概率为决策依据,对于难以当前决策的速度参数进行多假设延时决策,可有效解决低重频雷达径向速度估计问题.仿真试验表明,该方法在解速度模糊的同时可进行带径向速度量测的滤波,能较大程度地提高距离估计精度,并在一定程度上提高角度估计精度.
多参数;延时决策;贝叶斯航迹概率;速度模糊
1 引言
将速度量测引入滤波方程进行滤波处理,可以提高雷达多方面的性能,例如可以直接解线性调频信号距离多普勒耦合带来的距离走动、提高系统杂波滤除能力、提高点迹质量评估能力、提高目标状态估计精度、减少虚假航迹起始个数、提高点迹和航迹的正确关联概率等,但地面情报雷达根据使用特点多采用低重频的信号波形,使用该类波形测速通常存在速度模糊,在滤波处理中不能有效利用速度量测信息.为此,国际上在雷达测速及其快速算法[1~4]方面开展了广泛研究.
为了解决低重频雷达速度模糊问题,通常采用多脉冲重频参差技术[1,2],但该技术在快速傅里叶变换实现相参积累方面存在不便,工程应用中更多的是采用等重复周期的多脉冲工作,但该工作方式存在测速模糊.谢洁等[5]提出一种利用相邻回波脉冲的互相关函数进行测速的方法,该方法的估计误差大于不模糊速度,无法满足解模糊的工程应用需求.孟飞等[6]提出了利用最小二乘估计距离的导数,根据估计结果解算速度模糊,由于多数情况下距离的非线性变化,径向速度估计精度也很难满足解速度模糊条件.陈超等[7]提出了利用Kalman滤波所估计的径向速度来解速度模糊,该方法有效性取决于Kalman滤波精度,经过仿真分析该方法在有些情况下很难完全解决速度模糊问题.Abatzoglou[4]提出了极大似然方法的速度估计方法,该方法需要的脉冲数较多且运算量较大不易工程实现.本文针对地面情报雷达低重频波形的实际情况,提出了一种多参数延时决策模糊速度滤波方法,以贝叶斯航迹概率和序列似然比为基础,对于难于当前决策的速度模糊进行多假设延时决策,解速度模糊的同时进行带径向速度测量的滤波,在完成速度估计的同时,提高了距离估计精度,并在一定程度上提高了角度估计精度.
2 低重频雷达速度估计面临的问题
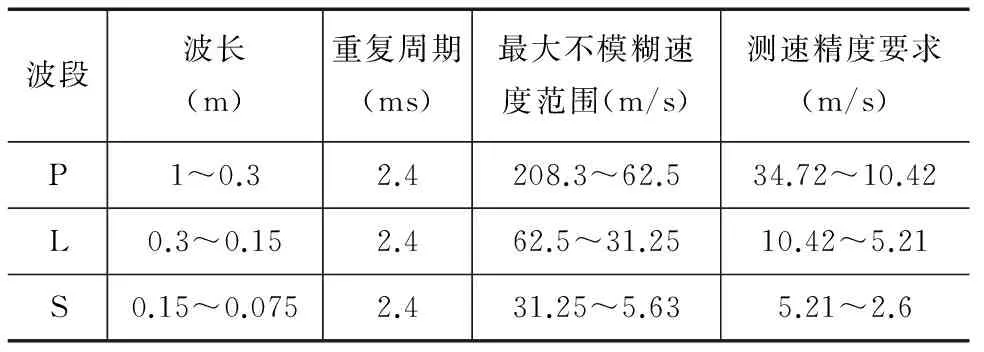
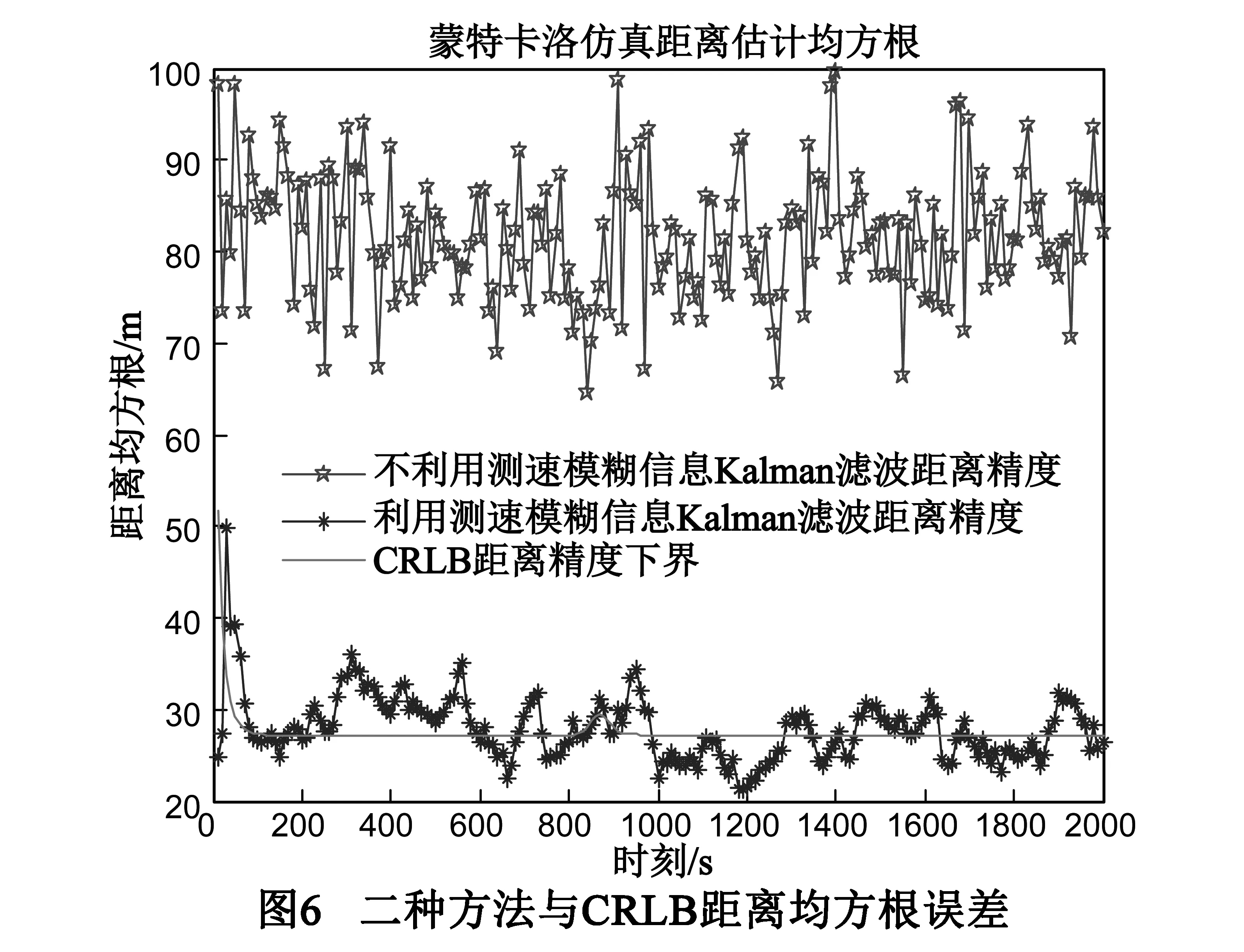
对于相同重复周期的低重频雷达,要想解决速度模糊问题,速度估计精度必须满足下式[8]:
|6σvr| 表1 P、L和S波段雷达最大不模糊速度范围 对于径向速度的估计,通常情况下有两种方法,即距离微分和Kalman滤波方法.距离微分径向速度估计精度[8]为: 其中σr为距离测量精度,T是目标的采样周期.通过仿真知道,Kalman滤波径向速度估计均方差大约是距离微分方法的1/2,但受到目标机动和测距精度的影响,速度估计精度会产生起伏.下面假定典型低频段雷达测距精度为100m,测角精度为0.2°,采样周期为10s,目标先匀速直线运动(0~800s)、然后匀速转弯(801~900s),最后匀速直线运动(901~2000s)的情况下,给出了Kalman滤波径向速度估计均方差(50次蒙特卡洛仿真). 从图1可以看出对于Kalman滤波估计的径向速度均方差在匀速直线运动段最大值为7.4m/s,在机动段最大值为18.1m/s.这在实际应用中很难达到解低脉冲重复频率雷达速度模糊的精度要求. 图2为利用Kalman滤波估计所得径向速度解速度模糊的误差.从图中可以看出在200次测量中共有14次模糊解算失败,失败百分比为7%,特别是在目标机动段更容易解速度模糊失败,在10次采样中4次解模糊失败,失败百分比达到了40%如果利用解模糊失败的径向速度进行滤波,将导致滤波的发散. 根据以上分析可知,利用估计径向速度解速度模糊有一定的局限性.为此本文提出了多参数延时决策解速度模糊的方法.该方法在滤波中加入多普勒测量值(如果存在n倍的模糊就需要2n+1个滤波器进行滤波和外推),对多次量测进行滤波处理,并进行模糊判决,由于正确径向速度所对应的滤波精度和贝叶斯航迹概率最高,可以有效解决速度模糊问题.由于该方法在滤波中增加了一维量测(多普勒),不仅提高了目标状态精度,还减小了关联门限,在工程应用中有一定价值. 多参数延时决策解速度模糊的基本思想就是对于当前无法决策的参数(速度模糊倍数),按照树状结构进行多假设递推,并依据一定规则(贝叶斯航迹概率),在未来某一时刻解决以前时刻的决策参数不确定问题(速度模糊倍数的不确定). 3.1滤波和数据互联 对于多个径向速度的假设,都要对航迹进行滤波外推,同时判断假定的量测是否满足互联门限,对于满足门限的进行滤波和外推.下面简单介绍数据互联和滤波方法. 数据互联采用关联门限算法.首先要确定跟踪门.跟踪门是跟踪空间中的一快子空间,中心位于被跟踪目标的预测位置,跟踪门大小的设计应保证以一定的概率接收正确回波,落入跟踪门内的量测即作为候选目标,也就是看目标的量测值z(k)(量测值除了距离和角度外,还包括径向速度)是否满足: (1) 雷达的观测数据与目标状态参数间的关系往往是非线性的,此时常常需要进行非线性滤波.常用的非线性滤波方法有EKF(Extended Kalman Filter)和UKF(Unscented Kalman Filter)算法,其中EKF是利用泰勒级数展开的线性化技巧将非线性滤波问题转化为一个近似的线性滤波问题,套用线性滤波理论得到求解原非线性滤波问题的次优滤波算法.由于其运算量小、算法简单,在工程中得到了广泛应用.UKF滤波算法是在UT[9](Unscented Transform)变换的基础上发展起来的,其精度相当于二阶泰勒展开的EKF算法,但运算量远远大于EKF算法.因此本文的仿真采用EKF算法,具体算法可参考文献[9]. 3.2多参数延时决策解速度模糊 多参数延时决策解速度模糊的基本思路是边滤波边决策.决策的依据就是贝叶斯航迹概率最高所对应的径向速度即为估计参数.例如根据事先分析,如果利用滤波径向速度解速度模糊可能存在n倍的模糊,则根据航迹概率从2n+1个决策参数中选取最佳的决策参数.大多数情况下,真实径向速度所对应的航迹概率较大(例如大于0.8),当需要模糊决策时(同时存在多个航迹概率较大的决策值),保留多条航迹外推滤波(例如可以每次只保留航迹概率最大的三条航迹,每次滤波后输出最大航迹概率所对应的目标状态),直到一条航迹概率明显高于其它航迹的概率时延迟决策结束,此时去除多余航迹,只保留一条航迹. 如果航迹预测到当前状态的径向速度为Vk,不模糊的最大速度为Vr,通过MTD测量得到的模糊速度为Vm,假设最多存在n倍的模糊,则待决策的径向速度为: Vl=Vr×(floor(Vk/Vr)+l)+Vm l=-n,-(n-1),…,0,…,n-1,n (2) 其中floor为取整函数. 则每次滤波径向速度的待决策的输入量为2n+1个,每一个径向速度都当作一维测量来参与滤波,则滤波结束后可以得到其相应的贝叶斯航迹概率: (3) 其中,PTk-1,l为上一时刻(k-1时刻)参数l对应的航迹概率;PTk,l为当前时刻(k时刻)参数l对应的航迹概率;LRk,l为当前时刻参数l对应的似然比, 如果2n+1个航迹概率的最大值绝对占优,则选取其对应的径向速度为测量的真实测量目标径向速度;否则选取三个或三个以上最大航迹概率所对应的径向速度进行多假设延时决策处理,直到其中一个航迹概率绝对占优为止,解除以前决策的不确定性.处理流程如图3所示. 下面先分析常规Kalman滤波和多参数延时决策对正确解速度模糊的概率,然后给出最优滤波的下界CRLB(Cramer-Rao Lower Bound)[10]. (4) (5) 而对于多参数延时决策解速度模糊,决策域扩大了2n+1倍,因此其单次解速度模糊的成功概率为: (6) N次估计解速度模糊成功的概率为: (7) 从式(4)和式(6)中可以看出,由于决策域的扩大,多参数延时决策方法提高了解速度模糊的正确概率. 下面以一个例子简单分析解速度模糊的成功概率.假设Kalman滤波径向速度估计精度为7.4m/s,最大不模糊速度为31.25m/s,则单次解速度模糊的成功概率为: 则200次量测速度估计全部解速度模糊成功的概率为: 也就是说在200次测量中至少发生一次解速度模糊失败的概率已经接近于1.假设多参数延时决策解速度模糊的参数个数为3,则单次解速度模糊的成功概率为: =0.9999999998 则200次量测速度估计全部解速度模糊成功的概率为: 也就是说在200次测量中利用多参数延时决策方法解速度模糊成功的概率接近于1. 根据文献[11]可知误差估计下界等效于递推估计的误差协方差矩阵: CRLB(k)=Pk/k 其中Pk/k是由Kalman滤波得到的k时刻目标状态估计误差协方差矩阵.如果此时得到的误差估计下界是直角坐标系误差协方差,可以通过如下方法得到距离、径向速度和方位角的均方根误差(假定目标和雷达在同一平面内).令: 假定:信号的脉冲重复周期Tr=2.4ms,脉冲个数N=4,信号波长λ=0.15m,目标信噪比为13dB,雷达测距精度100m,测角精度0.2°,采样周期为10s,采样点数为200点.目标先匀速运动、然后转弯运动最后匀速运动(参见图4).下面为利用多参数延时决策解速度模糊滤波和不利用速度模糊滤波的精度对比分析图(50次蒙特卡洛仿真结果).图5、图6和图7分别为径向速度、径向距离和方位滤波和CRLB下界估计结果对比分.两种方法估计均方根误差的均值参见表2. 表2 二种方法均方根与CRLB下界误差的均值 从图5、图6、图7和表2可以看出利用引入模糊径向速度进行滤波、并进行延时决策处理,距离和径向速度精度有较大程度的提高,基本上与CRLB下界重合,同时方位精度也有一定程度改善.仿真结果说明了多参数延时决策解速度模糊滤波方法的有效性. 本文针对地面雷达在低重频MTD工作方式下的测速模糊问题,提出了多参数延时决策解速度模糊滤波方法.该方法滤波利用了测速信息,并进行延时决策处理,可以克服利用距离微分或Kalman滤波估计径向速度精度不高而无法根本解决测速模糊问题,较大程度提高了距离和速度滤波精度,滤波精度基本上达到了CRLB下界,同时也改善了角度估计精度.由于在跟踪中利用了速度测量信息,对于杂波滤除、解决交叉混批和提高机动目标跟踪精度等难题也带来较大好处.本文方法具有一定的工程应用参考价值. [1]Zhou H,Wen B,Ma Z,et al.Range/Doppler ambiguity elimination in high frequency chirp radars[J].IEE Proceedings—Radar,Sonar and Navigation,2006,153(6):467-472. [2]Ferrari A,Berenguer C,Alengrin G.Doppler ambiguity resolution using multiple PRF[J].IEEE Transactions on Aerospace and Electronic Systems,1997,33(3):738-751. [3]Kay S.A fast and accurate single frequency estimator[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1989,37(12):1987-1990. [4]Abatzoglou T J,Gheen G O.Range,radial velocity,and acceleration MLE using radar LFM pulse train[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(4):1070-1083. [5]谢洁,杨文军,黎海林,等.低重复频率下的目标速度估计算法研究[J].现代雷达,2010,32(9):36-39. Xie Jie,Yang Wen-jun,Li Hai-lin,et al.A study on target velocity estimation under low PRF condition[J].Modern Radar,2010,32(9):36-39.(in Chinese) [6]孟飞,谢良贵,李饶辉.一种脉冲多普勒雷达解速度模糊新方法[J].系统工程与电子技术,2009,31(4):791-794. Meng Fei,Xie Liang-gui,Li Rao-hui.Novel method of velocity ambiguity resolution in pulse Dopper radar[J].Systems Engineering and Electronics,2009,31(4):791-794.(in Chinese) [7]陈超,王宇飞,强文义,等.低重频脉冲多普勒雷达解速度模糊新方法研究[J].战术导弹技术,2012,(1):50-53. Chen Chao,Wang Yu-fei,Qiang Wen-yi,et al.A new approach to resolve the velocity ambiguity of low repetition frequency pulse Doppler radar[J].Tactical Missile Technology,2012,(1):50-53.(in Chinese) [8]张光义.相控阵雷达原理[M].北京:国防工业出版社,2009. [9]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].北京:电子工业出版社,2006. [10]Van Tree H L.Detection,Estimation and Modulation Theory (Part I)[M].New York:Wiley,1968. [11]Xin Zhang,Willett P,Bar-Shalom Y.Dynamic Cramer-Rao bound for target tracking in clutter[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1154-1167. 周万幸男,1961年出生,浙江宁波人,1982年毕业于成都电子科技大学,现任中国电子科技集团公司第十四研究所所长,研究员级高级工程师,中国电子学会会士,先后荣获部优秀科技青年、部级有突出贡献专家、享受政府特贴专家、国家有突出贡献专家、江苏省“333”人才工程、光华工程科技奖(青年奖)等荣誉.主持并解决多项重大产品技术攻关,先后获电子部科技进步一等奖、电子部科技进步特等奖、国家科技进步一等奖和95全国十大科技成就奖等. E-mail:nrietqbs@126.com LPRF Radar Velocity Estimation Based on Multi-parameter Delay Decision ZHOU Wan-xing (NanjingResearchInstituteofElectronicsTechnology,Nanjing,Jiangsu210039,China) Introducing velocity measurement into track filtering can improve filtering accuracy,but velocity ambiguity in LPRF radar still exists,and range differential or Kalman filter cannot solve this problem completely.Thus,a new velocity ambiguity filtering method based on multi-parameter delay decision is proposed.According to Bayes track probability,multi-hypothesis delay decision can be performed on those velocity parameters that are difficult to be decided currently,so the problem of radical velocity ambiguity in LPRF radar will be solved effectively.Simulation results show that this method is helpful for velocity ambiguity resolution and radical velocity measurement filtering,thus range estimation accuracy can be improved significantly and angle estimation accuracy can be improved to a certain extent. multiple parameters;delay decision;Bayes track probability;velocity ambiguity 2014-07-10;修回日期:2015-06-05;责任编辑:梅志强 TN957.51 A 0372-2112 (2016)06-1279-06


3 基于多参数延时决策的低重频雷达速度估计

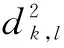

4 性能分析





5 数值仿真




6 结束语
