数值研究非平底地形对畸形波能量结构的影响*

崔　成，肖　辉，左书华，张义丰

(1.交通运输部 天津水运工程科学研究所，天津 300456；2. 港口水工建筑技术国家工程实验室，天津 300456)



数值研究非平底地形对畸形波能量结构的影响*

崔成1,2，肖辉1,2，左书华1,2，张义丰1,2

(1.交通运输部 天津水运工程科学研究所，天津 300456；2. 港口水工建筑技术国家工程实验室，天津 300456)

采用流体体积(VOF)方法捕捉自由表面，结合有限差分方法求解N-S(Navier-Stokes)方程、k-ε模型封闭，建立数值模型，并使用该模型模拟非平底地形条件下畸形波的生成。采用小波分析方法计算模拟结果的时频能量谱，基于计算结果分析非平底地形对畸形波能量集中程度和高频能量的影响。主要结论为：坡度小于1∶10的斜坡地形和无量纲水深变化小于0.333的曲线地形对畸形波时频能量谱的影响不显著；坡度大于1∶10的斜坡地形和无量纲水深变化大于0.333的曲线地形会显著影响畸形波的时频能量谱，随着坡度和无量纲水深变化的增加，时频能量谱中畸形波发生时刻附近，能量向高频方向移动，使得能量在高频端的分布范围增大，时频谱密度峰值减小；斜坡和曲线地形的特征变化对于畸形波能量集中度参数的影响不显著。

畸形波；能量结构；非平底地形

畸形波是一种包含在随机波列当中的单个异常大波，具有明显的非线性特征，持续时间短，能量集中，破坏力惊人[1]。随着人类对海洋的开发和利用不断发展，关于畸形波的研究已经引起越来越多国内、外学者的关注。目前，畸形波的生成机理还没有定论，根据畸形波发生的环境条件以及内部、外部特征，学者们提出了一些假说，如：组成波波能聚焦作用、波流相互作用、大气与海水的相互作用、地形作用、波浪调制不稳定机制、波浪间的非线性相互作用等[2]，这些假说在逐渐被证明的过程中。

上述可能引发畸形波的因素各自并非独立存在，而且之间也存在复杂的联系。因此一次畸形波事件可能不仅是一种生成机制引发，可能为上述两种或两种以上生成机制。对于近岸较浅水域，地形变化条件普遍存在，如果满足有限水深条件(水深与特征波长之比小于0.5)，则地形对波浪传播、演变的影响则不能忽视。当波浪经过复杂地形从较深水域传播至较浅水域的过程中，复杂地形对波浪的反射，折射和变浅作用会改变波浪的传播形态和能量传递过程。Biausser等[3]和Guyenne等[4]数值模拟了孤立波在水深不断变浅的非平底地形上的传播演化过程，结果显示未发生破碎之前，随着水深的不断减小，能量不断的积累，波高和波陡不断的增加。Sergeeva等[5]使用KDV方程模拟了随机波列在不规则地形上的传播和变形，研究结果发现波高随地形的起伏而变化，且波高的分布偏离Rayleigh分布，大波的发生概率随地形突变个数的增多而增大；相对于平底地形，当波列在不规则地形上传播演化时，畸形波的发生概率明显提高。裴玉国[6]的物理试验结果也得到了相似的结论。由此可见地形作用可能是引发畸形波的因素之一。在有限水深条件下，研究水底地形对畸形波的影响有助于解释畸形波的生成机理。畸形波的内部能量结构决定其外部特征，能更加直观地描述畸形波的形成机制。小波分析方法可以有效地捕捉畸形波发生时的能量分布状态，已有学者使用小波分析方法开展了有关畸形波时频能量谱的研究。主要研究结果表明，畸形波的小波谱具有十分明显的特征，能量集中且包含大量的高频成分，非线性相互作用明显，部分实测畸形波的小波谱还表现出双峰特征[7-11]。由此可见，对畸形波能量结构的研究可以重点关注高频能量成分和能量集中程度两个方面。

本文采用流体体积(VOF)方法捕捉自由表面，并结合有限差分方法求解N-S(Navier-Stokes)方程建立数值模型；运用双波列叠加模型(组成波聚焦机制)模拟非平底地形条件下(地形作用)畸形波的生成；采用小波分析方法计算模拟畸形波的时-频能量谱；根据计算结果进一步分析地形条件变化对其内部能量特征的影响。

1数学模型建立和验证

1.1控制方程

考虑到畸形波的波陡很大，在其形成过程中能量不断汇聚，流体湍动效应显著，因此考虑适当的湍流模型。对非稳态的Navier-Stokes方程进行时间平均运算，得到雷诺时均方程，并利用目前应用范围广、检验程度高的k-ε模型建立紊流脉动值附加项与其他时均值之间的联系，来封闭雷诺时均方程，与连续方程一起作为控制方程，见式(1)～(5)。

连续方程：

(1)

雷诺时均方程：

(2)

(3)

双方程k-ε模型：

(4)

(5)

式中，u和v分别表示x和y方向的速度分量；θ表示部分单元参数，不依赖于时间，依据网格中流体的比例，取值为0～1；p为流体压力；ρ为流体的密度；ν为流体的运动黏滞系数；νt=Cu(k2/ε)，为湍动黏滞系数；k表示湍动能；ε表示湍动能耗散率。k-ε方程中的经验参数分别选为：Cu=0.09，σk=1.0，σε=1.3，σε1=1.43，Cε2=1.92[12]。

1.2边界条件

1.2.1造波边界条件

造波边界条件采用双波列叠加模型计算，见式(6)。该模型中，目标谱能量被分成2部分：一部分能量分配给瞬态波列，另一部分分配给常规随机波列[13]。

(6)

式中，η(x,t) 表示距离造波板x处的波面时间过程；η1(x,t) 和η2(x,t) 分别表示常规随机波列和瞬态波列的波面时间过程；ki，ωi(ωi在第i个频域区间上随机选取，为避免波浪以周期2π/Δω重复出现)和εi(0～2π内均匀分布)分别表示第i个组成波的波数，角频率和随机初相位；xc和tc分别表示瞬态波的聚焦时间和位置；a1i和a2i分别表示两波列第i个组成波的振幅，由式(7)确定：

(7)

式中，p1=80%，p2=20%，该分配比例能生成满足定义的畸形波[13]；S(f)表示谱密度函数，本文选用修正的P-M谱[14]作为目标谱，表达式见式(8)：

(8)

式中，T表示平均周期;Hs表示有效波高。

根据造波原理，造波边界的水平速度U0(t)可表示为

(9)

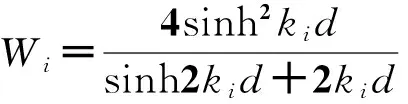
1.2.2吸收边界条件

为了限制计算域，在水槽的右端设置一个吸收边界层来吸收出流波浪。在吸收边界区域中，速度和自由表面等变量分别衰减为：v(x,y)/μ(x)，η/μ(x)，k/μ(x)和ε/μ(x)。μ(x)为衰减系数：

(10)

式中，λ为吸收区域的长度；λ′为吸收区域内的点到水槽右端边界的距离；α为阻尼系数。

1.3数值模型验证

为了验证所建立数值模型模拟畸形波的有效性，使用该数值模型模拟一组畸形波。计算区域如图1所示，在x和y方向分别划分1 600和30个单元格，计算域右端设置30 m吸收区域。在x和y方向单元格间距分别为5和3 cm，计算时间220 s，时间间隔0.01 s，运动黏性系数1.002×10-6m2/s。验证采样点距离造波边界2 100 cm。数值模拟中畸形波模拟方法及验证点位置均与物理试验相匹配。物理试验在大连理工大学海岸及近海工程国家重点实验室的浑水水槽中进行，该水槽长56 m，宽3 m，最大工作水深0.7 m。图2给出了数值模拟畸形波波面时间过程与物理实验结果的对比。从图2的对比可以看出，本文所建立的数值模型可以较准确地模拟具有较强非线性的畸形波。图2b为局部放大图。

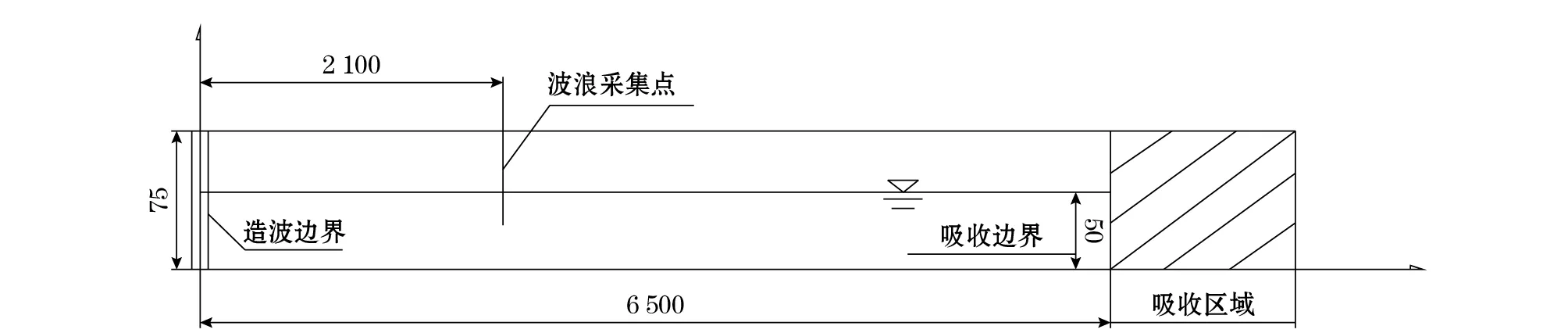
图1　数值模型计算域的布置图(cm)Fig.1　Setup of the numerical modeling domain

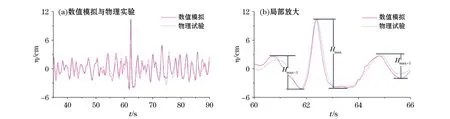
图2　畸形波波面时间过程数值模拟与物理实验结果的对比Fig.2　Comparison of the simulated and experimental freak waves

为了验证该数值模型模拟非线性波浪在非平底地形上传播的有效性。使用该数值模型模拟孤立波在1∶20斜坡上传播的分裂现象，水深从d0=7.62 cm 逐渐变为d1=3.81 cm。计算域与Madsen和Mei[15]所做的物理实验相匹配，见图3。孤立波波要素为：振幅0.91 cm，传播速度91.96 cm/s。边界条件，网格尺寸和时间步长都与Choi和Wu[16]给出的数值模拟算例一致。图4给出了模拟结果对比，为了方便对比统一将a位置波峰对应时刻设置为0 s。总体看来，三者基本一致，在水深逐渐变浅的斜坡上，波面发生了分裂现象，在孤立波的右侧出现了一个较小的波浪。与Choi和Wu[16]数值结果的差异是由于本文数值模型考虑黏性耗散的影响，而前者未考虑黏性耗散。比较而言，本文的模拟结果无论是相位还是峰值，与Choi和Wu的数值结果相比都更为接近物理模拟结果。上述结果表明，本文所建立的数值模型模拟较强非线性波浪在地形上传播和演化过程具有较好的精度和稳定性。

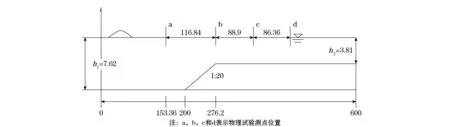
图3　孤立波在斜坡地形上传播的布置图(cm)Fig.3　Setup of a solitary wave propagation over an non-flat bottom

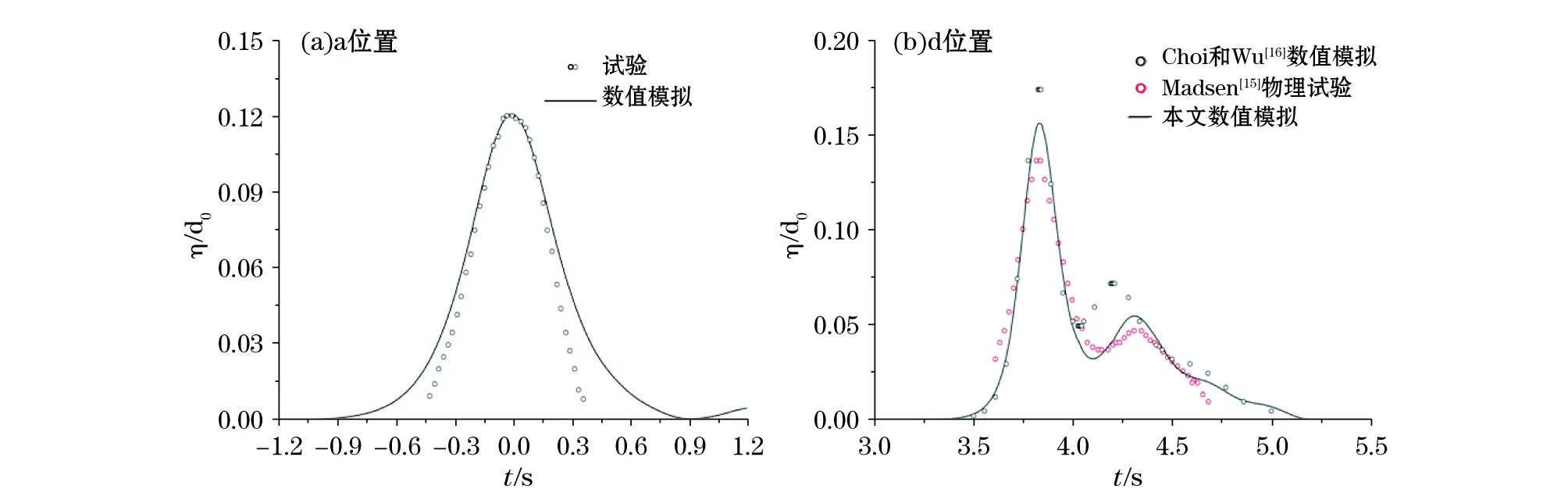
图4　孤立波传播、演化过程的数值结果验证示例Fig.4　Comparison of the modeled and the experimental solitary wave propagating over a non-flat bottom

2　数值计算组别

本文考虑两种非平底地形，分别为斜坡地形和抛物曲线地形。对于斜坡地形，模拟了8组不同坡度的斜坡，坡度在1∶25 ～ 1∶5.6范围内变化。斜坡地形边界和计算域参见图5。将数值水槽分为3部分，设造波边界为原点，X=0～1 250 cm为平底地形，水深为d0=150 cm；X=1 250～2 000 cm为斜坡地形，水深从d0变化到d1，对应8组坡度坡顶的水深d1在120～15 cm变化；X=2 000～6 500 cm为平底地形，水深为d1。对于抛物曲线地形，模拟了6组抛物曲线地形，地形最大高度在30～130 cm范围内变化。抛物曲线地形边界和计算域参见图6。X=0～1 250 cm为平底地形，水深为d0=150 cm；X=1 250～2 750 cm为抛物曲线地形，水深从d0变化到d1，对应6组曲线地形，坡顶的水深d1在120～20 cm变化，地形曲线由抛物线方程确定；X=2 750～6 500 cm为平底地形，水深为d0。

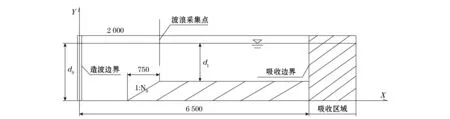
图5　斜坡地形的计算域示意图Fig.5　Sketch of the numerical modeling domain with a slope

图6　曲线地形的计算域示意图(cm)Fig.6　Sketch of the modeling domain with bump bottom

表1汇总给出了数值模拟算例组别。表中Ls为有效波长(有效周期对应的波长)；Δd/d0为无量纲水深变化，其中Δd=d0-d1。表2给出模拟畸形波的特征参数。

所有模拟组别中，入射波条件相同，均为有效波高Hs=5 cm，有效周期Ts=1.4 s。无论平底地形(Case 1)还是非平底地形(Case 2～Case 15)均得到了满足定义的畸形波，即波高H0大于等于波列有效波高Hs的2倍，α1=H0/Hs≥2，波高H0大于等于与该波浪相邻波浪波高的2倍，α2=H0/H-1≥2和α3=H0/H+1≥2，波峰η0大于等于波高的0.65倍，α4=η0/H0≥0.65。

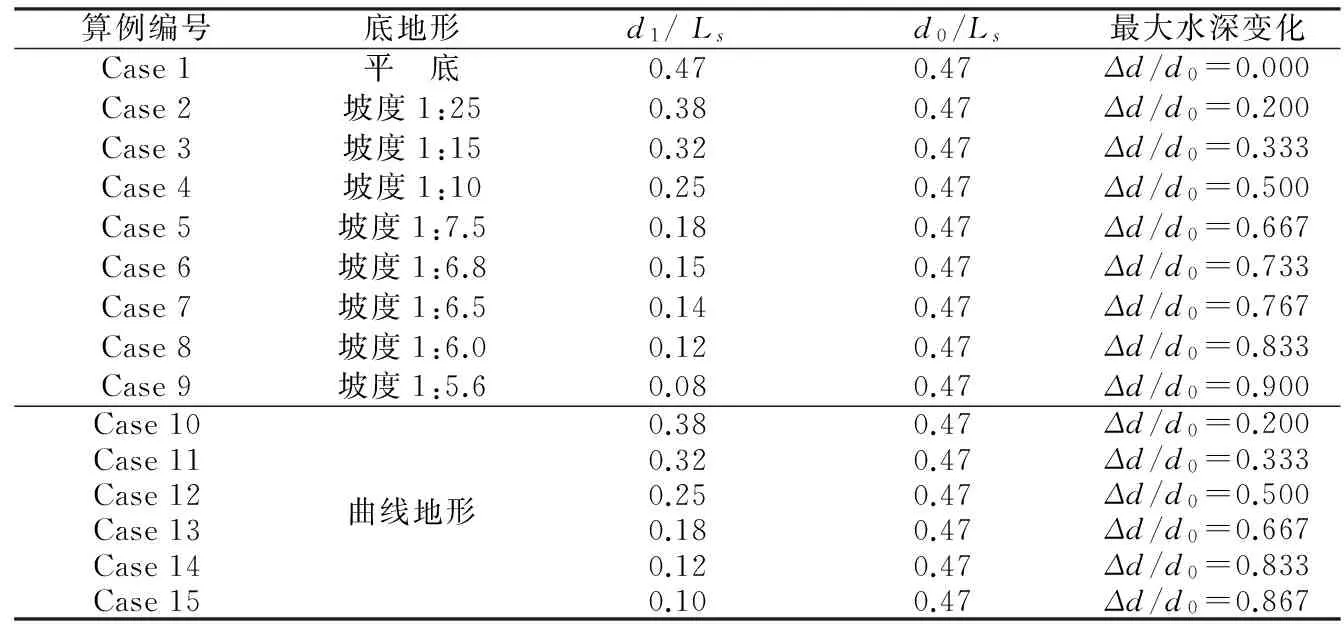
表1　数值模拟组别

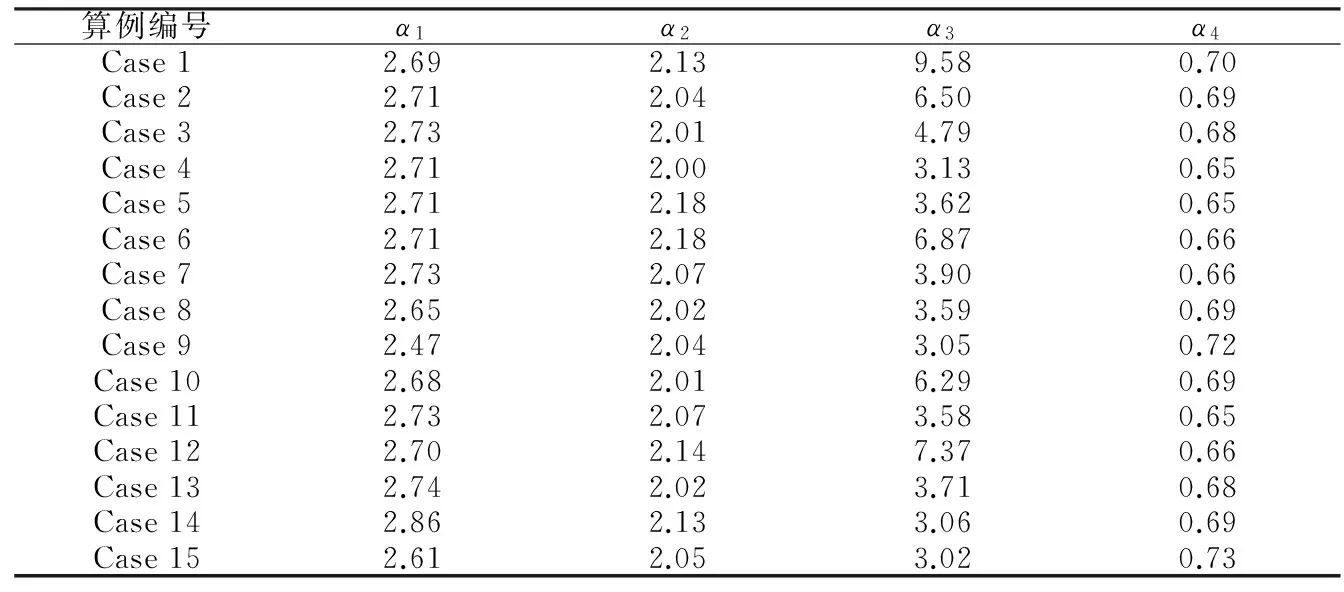
表2　畸形波特征参数

3　小波谱计算和分析

3.1小波谱计算方法

将包含畸形波的连续波浪序列做连续小波变化：

(11)

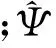
(12)

定义无量纲时频能量谱密度S*(f*,T*)：

(13)

式中，f*为无量纲频率，f*=f/fp；f表示频率；fp表示谱峰频率；T*为无量纲时间；T*=(t-tc)/Tp；tc表示畸形波生成、演化过程中发生异常大波波峰对应时刻，Tp表示谱峰周期。

3.2小波谱分析

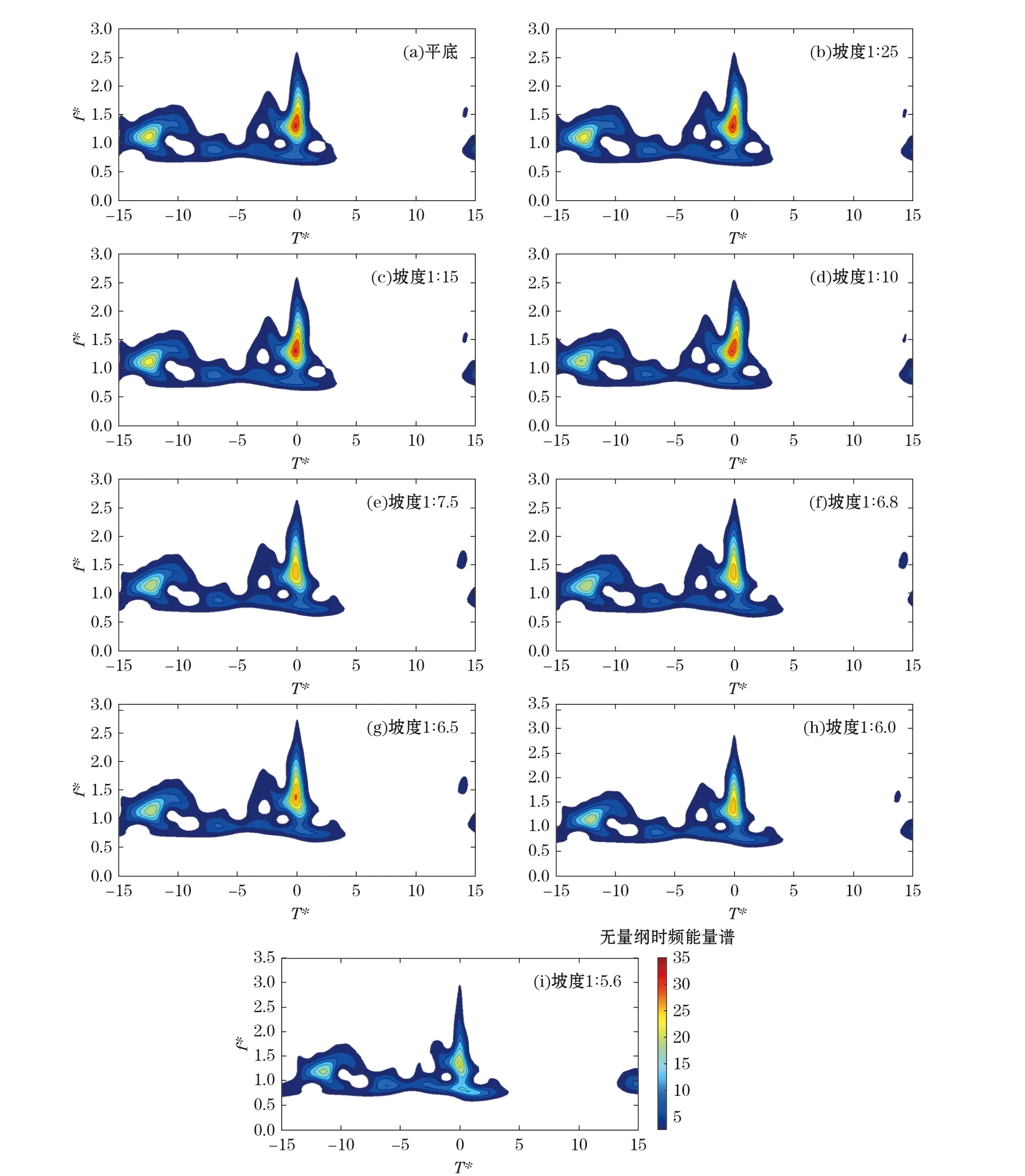
图7　平底和斜坡地形条件下畸形波的无量纲时频能量谱Fig.7　Non-dimensional time-frequency spectrums of freak waves for cases 1～9

图7给出了平底地形(Case 1)及8组斜坡地形(Case 2～Case 9)条件下畸形波的时频能量谱。从图7中可以看出：当坡度s从0增长到1∶10时，畸形波的时频能量谱基本没有变化；当坡度s从1∶10增长到1∶5.6时，在畸形波发生时刻附近，能量有向高频端移动的趋势；无量纲时频谱密度峰值由30～35降到20～30；能量在高频端的分布范围变大，在坡度为1∶5.6的斜坡地形条件下，高频端能量分布范围可达3倍的谱峰频率(平底地形条件下，高频端能量分布范围为2.5倍的谱峰频率)。

图8给出了平底地形(Case 1)及6组抛物曲线地形(Case 10～Case 15)条件下畸形波的时频能量谱。由图8可知：当Δd/d0从0增长到0.333时，畸形波的时频能量谱基本没有变化；当Δd/d0从0.333增长到0.867时，在畸形波发生时刻附近，能量有向高频端移动的趋势；无量纲时频谱密度峰值由30～35降到20～30；能量在高频端的分布范围变大，在Δd/d0=0.867的曲线地形条件下，高频端能量的分布范围可达4倍的谱峰频率。

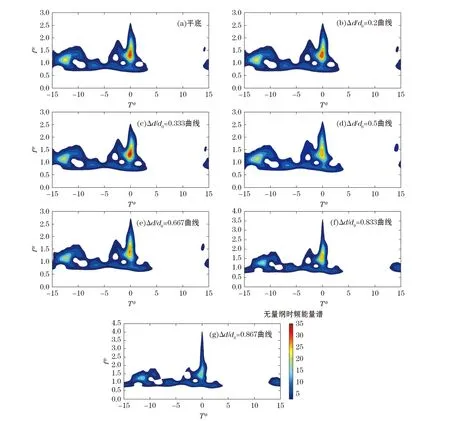
图8　平底和曲线地形条件下畸形波的无量纲时频能量谱Fig.8　Non-dimensional time-frequency spectrums of freak waves for cases 1, 10～15

由此可见，坡度s小于1∶10的斜坡地形和无量纲水深变化Δd/d0小于0.333的曲线地形，对畸形波时频能量谱的影响不显著；而对于坡度大于1∶10的斜坡地形和无量纲水深变化Δd/d0大于0.333的曲线地形，会显著影响到畸形波的时频能量谱。随着s和Δd/d0的增加，在畸形波时频能量谱中，畸形波发生时刻附近，能量向高频端移动，使得能量在高频端的分布范围增大，时频谱密度峰值减小。

为了进一步量化分析地形变化对畸形波时频能量谱的影响，图9给出了畸形波能量集中程度参数αE随地形特征变化的情况。

其中畸形波能量集中程度参数αE定义为对于某特定时刻，各频率成分的总能量Ec：

(15)

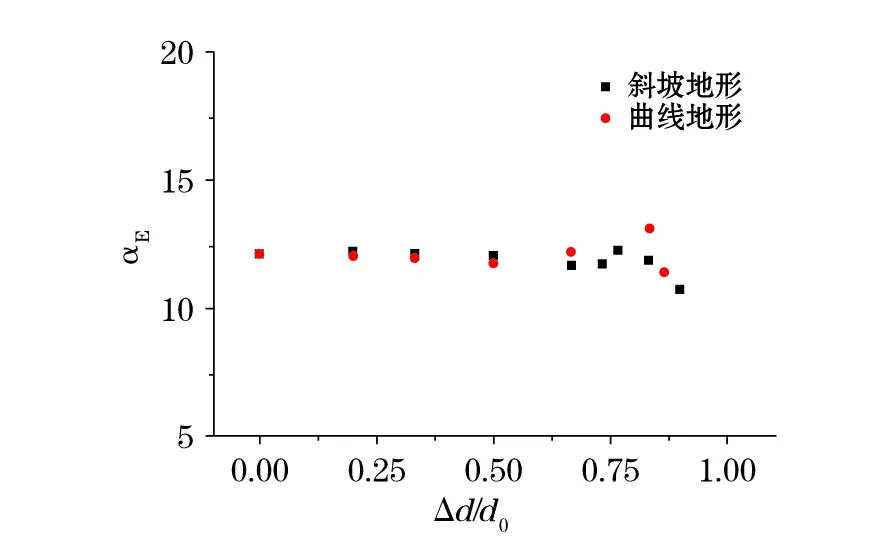
图9　畸形波αE随坡度的变化Fig.9　Relationship between the slope s and αE of freak waves for cases 1～15

(16)

则能量集中度参数αE：

(17)

从图9中可以看出，随着Δd/d0的增加，畸形波能量集中度参数αE变化很小，两种地形条件下能量集中度参数αE的变化情况一致。

除能量集中度外，另一畸形波能量特征为包含较多高频成分，为了定量分析地形变化对畸形波高频能量的影响，计算15组算例畸形波周期时段内，2倍谱峰频率以上频率成分能量和Eh及各频率成分总能量Et。图10给出了2种地形条件下，畸形波Eh/Et随地形特征的变化,其中s表示斜坡坡度。

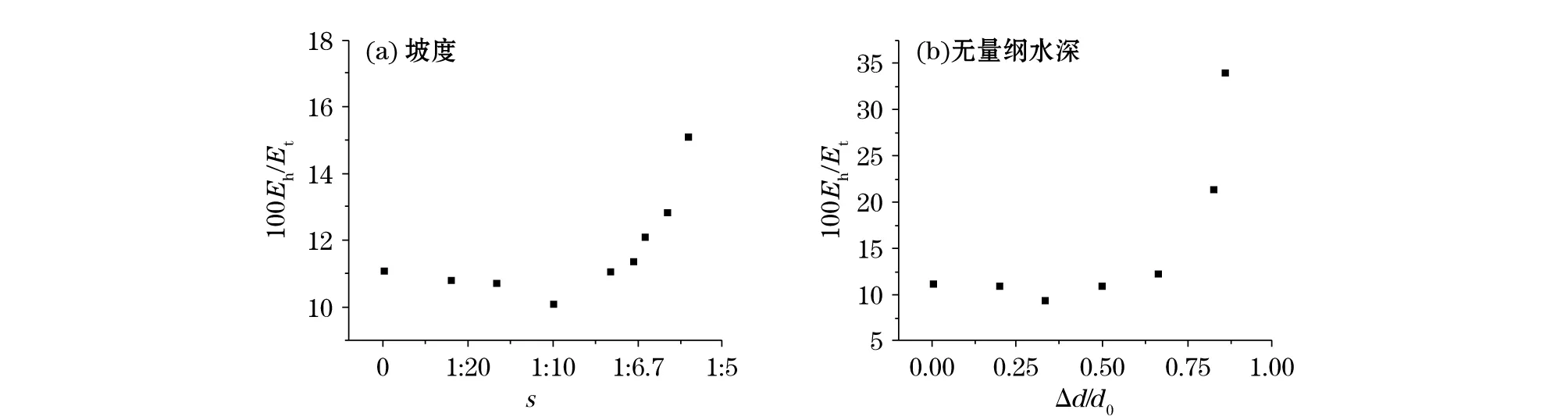
图10　畸形波Eh/Et随地形特征的变化Fig.10　Relationship between the slope s and Eh/Et of the freak waves for cases 1～15

从图10中可以看出：斜坡地形条件下s≤1∶6.5时和曲线地形条件下Δd/d0≤0.667时，地形变化对Eh/Et的影响不显著(相对于平底地形算例的变化幅度≤10%)；对于斜坡地形条件，当坡度s≥1∶6.0时，变化幅度有一定程度的增长，在20%～40%之间，Eh/Et随着坡度的加大而增加；对于曲线地形条件，当Δd/d0≥0.833时，变化幅度增长明显，在90%～310%之间，Eh/Et随着坡度的加大而增加。曲线地形条件下无量纲水深变化Δd/d0对Eh/Et的影响远远大于斜坡地形条件下坡度s对Eh/Et的影响。

4　结　论

基于数值模拟结果，采用小波分析方法计算畸形波的时-频能量谱，通过分析斜坡地形和曲线地形特征变化对时-频能量谱的影响主要得到如下结论：

1)坡度小于1∶10的斜坡地形和无量纲水深变化小于0.333的曲线地形，对畸形波时频能量谱的影响不显著；对于坡度大于1∶10的斜坡地形和无量纲水深变化大于0.333的曲线地形，对畸形波的时频能量谱有一定影响。随着坡度和无量纲水深变化的增加，畸形波发生时刻附近，能量向高频端移动，使得能量在高频端的分布范围变大，时频谱密度峰值减小。

2)斜坡和曲线地形的特征变化对于畸形波能量集中度参数αE的影响不显著。

3)坡度小于1∶6.5和无量纲水深变化小于0.667算例，地形变化对2倍谱峰频率以上高频成分的影响不显著；当坡度大于1∶6.0和无量纲水深变化大于0.833时，随着坡度和无量纲水深变化的增加，2倍谱峰频率以上高频成分明显增加。

[1]CUI C. Study on generation、evolution and internal structures of freak waves[D].Dalian:Dalian University of Technology, 2013.崔成.畸形波生成、演化及内部结构研究[D].大连:大连理工大学,2013.

[2]KHARIF C, PELINOVSKY E. Physical mechanisms of the rogue wave phenomenon[J].European Journal of Mechanics B/Fluids, 2003,22:603-634.

[3]BIAUSSER B, GRILLI S T, FRAUNIE P. Numerical analysis of the internal kinematics and dynamics of three-dimensional breaking waves on slopes[C]∥Proceeding 13th Offshore and Polar Engineering Conference, USA, 2003:340-346.

[4]GUYENNE P, GRILLI S T. Computations of 3D overturning waves in shallow water[C]∥Proceeding 13th Offshore and Polar Engineering Conference, USA, 2003:347-352.

[5]SERGEEVA A, PELINOVSKY E, TALIPOVA T. Nonlinear random wave field in shallow water: variable Korteweg-de Vries framework[J].Natural Hazards and Earth System, 2011,11(2):323-330.

[6]PEI Y G. The generation of freak waves and its Behaviors[D].Dalian: Dalian University of Technology, 2007.裴玉国.畸形波的生成及基本特性研究[D].大连:大连理工大学,2007.

[7]LIU P C, MORI N. Wavelet spectrum of freak waves in the ocean[C]∥Proceedings, 27th International conference on Coastal Engineering, ASCE, 2000:1092-1098.

[8]CHIEN H, KAO C C. On the characteristics of observed coastal freak waves[J].Coastal Engineering Journal, 2002,44(4):301-319.

[9]CHRISTOU M., EWANS K., BUCHNER B, et al. Spectral characteristics of an extreme crest measured in a laboratory basin[J/OL]. http:∥www.ifremer.fr/web-com/stw2008/rw/full/Christou.pdf.

[10]ZHAO X Z. Experimental and numerical study of freak waves[D].Dalian: Dalian University of Technology, 2008. 赵西增.畸形波的实验研究和数值模拟[D].大连:大连理工大学,2008.

[11]CUI C, ZHANG N C. Research on the time-frequency energy structure of generation and evolution of freak wave[J].The Ocean Engineering, 2011,29(3):59-66.崔成,张宁川.畸形波生成、演化过程时频能量结构研究[J].海洋工程,2011,29(3):59-66.

[12]RODI W. Turbulence models and their application in hydraulics[C]∥IAHR Monograph，1984(8)：58.

[13]KRIEBEL D L. Efficient simulation of extreme waves in a Random Sea[J/OL].http:∥www.ifremer.fr/metocean/conferences/stw_abstracts/kriebel.pdf.

[14]YU Y X, LIU S S. Random wave and its applications to engineering[M].Dalian: Dalian University of Technology Press, 2011.俞聿修,柳淑学.随机波浪及其工程应用[M].大连:大连理工大学出版社,2011.

[15]MADSEN O S, MEI C C. The transformation of a solitary wave over uneven bottom[J].Journal of Fluid Mechanics, 1969,39:781-791.

[16]CHOI D Y, WU C H. A new efficient 3D non-hydrostatic free-surface flow model for simulating water wave motions[J].Ocean Engineering, 2006,33:587-609.

[17]TORRENCE C, COMPO G P. A practical guide to wavelet analysis[J].Bulletin of the American Meteorological Society, 1998,79(1):61-78.

Numerical study on the effects of non-flat bottom topography on the energy structure of freak waves

CUI Cheng1,2，XIAO Hui1,2，ZUO Shu-hua1,2，ZHANG Yi-feng1,2

(1.TianjinResearchInstituteforWaterTransportEngineering，M.O.T.,Tianjin 300456,China;2.NationalEngineeringLaboratoryforPortHydraulicConstructionTechnology，Tianjin 300456，China)

A numerical model that solves the Reynolds time-averaged N-S equations by the finite-difference method was built with the k-ε model for the turbulence closure and the volume of fluid (VOF) method for tracking the free surface. The model was implemented to simulate the freak waves over non-flat bottom topography. With the time-frequency energy spectrum of the freak waves that was calculated by the wavelet analysis method the effects of non-flat bottom topography on the energy focusing and high frequency energy were analyzed. It is concluded that the non-flat bottom topography has a insignificant effect on the time-frequency energy spectrums for the slope that is less than 1∶10 and the topography whose normalized change in water depth is smaller than 0.333, but the influence of the non-flat bottom topography is considerable for the slope that is more than 1∶10 and the topography whose normalized change in water depth is greater than 0.333. With the increasing slope and normalized change in water depth, the energy shifts to high frequency endwhich makes the frequency domain of the energy distribution broaden, and the peak value of the time-frequency spectrum density decreases. On the other hand, the non-flat bottom topography has a indifferent effect on the parameters of energy focusing.

freak wave; energy structure; non-flat bottom topography

August 18, 2015

2015-08-18

国家自然科学基金项目——量化分析三维畸形波内部结构(51509120)

崔成(1984-)，男，辽宁海城人，博士，主要从事波浪、潮流模拟及其与结构物相互作用方面研究.E-mail：chengcui1984@163.com

(陈靖编辑)

P731

A

1671-6647(2016)03-0377-11

10.3969/j.issn.1671-6647.2016.03.007