一种建立南海浅海海域高精度潮汐模型方法的研究*

雷　宁，付延光，杨　龙，周兴华，阳凡林，王朝阳，孙维康

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266510；2.国家海洋局 第一海洋研究所，山东 青岛 266061)



一种建立南海浅海海域高精度潮汐模型方法的研究*

雷宁1，2，付延光1,2，杨龙2*，周兴华1,2，阳凡林1，王朝阳1，孙维康1

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266510；2.国家海洋局 第一海洋研究所，山东 青岛 266061)

针对应用高度计数据建立的海潮模型在浅海海域精度较低的现状，提出采用移去-恢复技术联合利用19 a T/P、Jason-1卫星原始轨道、变轨轨道高度计数据建立南海浅海海域高精度潮汐模型的方法。处理卫星高度计数据时以平均海平面为基准面，按纬差0.1°间隔采用沿迹分析提取南海海域原始轨道2 184个正常点和变轨轨道1 626个正常点；分别对原始轨道、变轨轨道正常点进行调和分析以及响应分析，得到潮汐主要分潮调和常数；进一步建立网格潮汐模型，讨论了不同分辨率潮汐模型的精度差异。基于验潮站数据集结果运用移去-恢复技术对所建潮汐模型进行改进，改进后潮汐模型4个最主要分潮O1，K1，M2和S2的RMS分别提高至7.76，9.40，13.86和8.51 cm，RSS达到20.32 cm，表明移去-恢复技术能够明显改善潮汐模型在浅海海域的精度。

卫星测高；潮汐模型；调和分析；响应分析；移去-恢复技术

随着卫星测高技术的发展，近几年国际上推出的全球海洋潮汐的模型在精度、分辨率和覆盖范围等方面均取得较大的进步。受海洋动力和陆地反射的影响，基于卫星高度计数据建立的海洋潮汐模型在浅海海域存在较大的误差[1-2]，严重影响了高度计数据在浅海海域的应用，研究如何提高潮汐模型在浅海海域的精度至关重要。

卫星测高技术为建立全球海潮模型提供了丰富的海洋潮汐信息，极大地推动了对海洋潮汐的研究。对于南海海域潮汐模型的研究，王延强等[3]利用18.6 a的T/P系列高度计数据建立了6′×6′网格潮汐模型，孙佳龙等[4]利用11 a的T/P高度计数据构建了1°×1°潮汐模型，许军等[5]联合T/P与Geosat/ERM高度计资料建立了10′×10′潮汐模型，结果表明，采用不同分辨率构建的潮汐模型精度不同。对于全球海潮模型精度的分析，汪一航等[6]依据中国近海18个岛屿的调和常数对5个潮汐模型(NAO.99b，GOT00，FES2002，FES2004，TPXO7.2)的准确度进行了检验，结果表明全球海潮模型NAO.99b在中国近海的结果相对准确。Gladkikh等[7]利用新西兰沿岸7个验潮站分析了全球海洋潮汐模型TPXO7.2，GOT00.2，NAO.99b，FES2004和EOT10a的准确度，结果表明在新西兰沿岸TPXO7.2与验潮站数据符合最好。高秀敏等[8]采用南海海域60个验潮站和22个TOPEX/Poseidon高度计轨道交叉点的调和常数对比了TPXO7.2，GOT00.2，NAO.99b和DTU 10四种全球海洋潮汐模型O1，K1，M2和S2四个最主要分潮调和常数在南海的准确度，结果表明，南海海域DTU10准确度最高。

针对以上情况，本文利用19 a的T/P，Jason-1卫星高度计数据，其中原始轨道数据时间序列为16 a，变轨轨道数据时间序列为6 a，分别进行调和分析及响应分析，讨论了建立不同分辨率潮汐模型精度的差异。并针对浅海海域，提出采用移去-恢复技术对潮汐模型进行改进，选取全球海潮模型TPXO7.2[9-10]，NAO.99b[11]和DTU10[12]进行对比分析，通过实验验证此方法的有效性。

1　高度计数据处理与移去-恢复技术

1.1高度计数据处理

研究范围为(0°～26°N，99°～121°E)，高度计数据采用美国NASA喷气推进实验室的T/P高度计MGDR-B数据以及法国空间局国家研究中心(CNES)的Jason-1高度计GDR-C数据，采用时间分布情况列于表1，高度计轨迹分布见图1。

表1　采用的卫星高度计数据

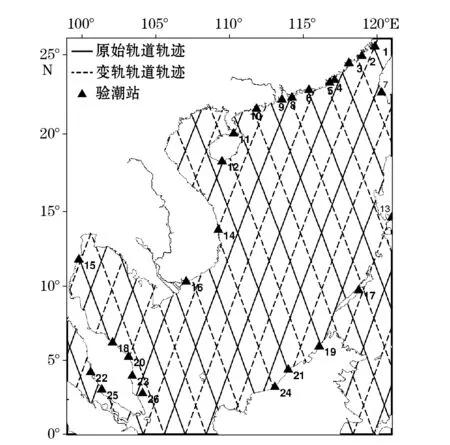
图1　T/P系列高度计轨迹和验潮站分布图Fig.1　T/P series altimeter tacks in the South China Sea

高度计数据预处理主要包含两方面：潮高计算和轨迹正常点的计算。

1)潮高计算。以平均海平面作为基准面，对高度计数据实施除海潮改正外的其他各项改正，本文参考暴景阳和许军[13]研究。

2)轨迹正常点的计算。采用沿迹纬差6′间隔的方式，对潮高采用最小二乘拟合计算，经度取所有周期重复点的经度平均值。据此生成原始轨道沿迹2 184个正常点16 a潮高时间序列，以及变轨轨道1 626个正常点6 a潮高时间序列。

对原始轨道正常点进行调和分析[14]得到12个主要分潮(Sa，Ssa，Mm，Mf，Q1，O1，P1，K1，N2，M2，S2和K2)的调和常数；对变轨轨道正常点进行响应分析[15]得到8个主要分潮(Q1，O1，P1，K1，N2，M2，S2和K2)的调和常数。

1.2移去-恢复技术

移去-恢复法是最先应用在大地水准面精化中的一种局部重力场逼近的组合法，其基本原理是将研究对象ζ分解成低频分量Δζ和高频分量Δζres两部分[16]，见式(1)。

(1)

式中，低频分量Δζ由已有模型作为参考量计算得到，而高频分量Δζres由该模型与已知点真值的残差模型计算得到，这种技术就是移去-恢复技术。

事实上，受气象、海洋动力和海岸地形等因素的影响，分潮调和常数存在一定量级的趋势性或周期性变化成分，是一种非常数型参数[17-18]。对浅海海域而言，采用高度计数据进行潮汐信息提取还受到高频混淆的影响，提取的潮汐信息与验潮站结果存在一定的差异。为改善其精度，将分潮的调和常数分解为两个部分进行处理，即采用移去-恢复技术。为避免高频、低频分潮的概念混淆，本文将分解的两部分定义为模型分量和残余分量，即式(1)中Δζ和Δζres。应用移去-恢复技术的具体操作流程[19]见图2。

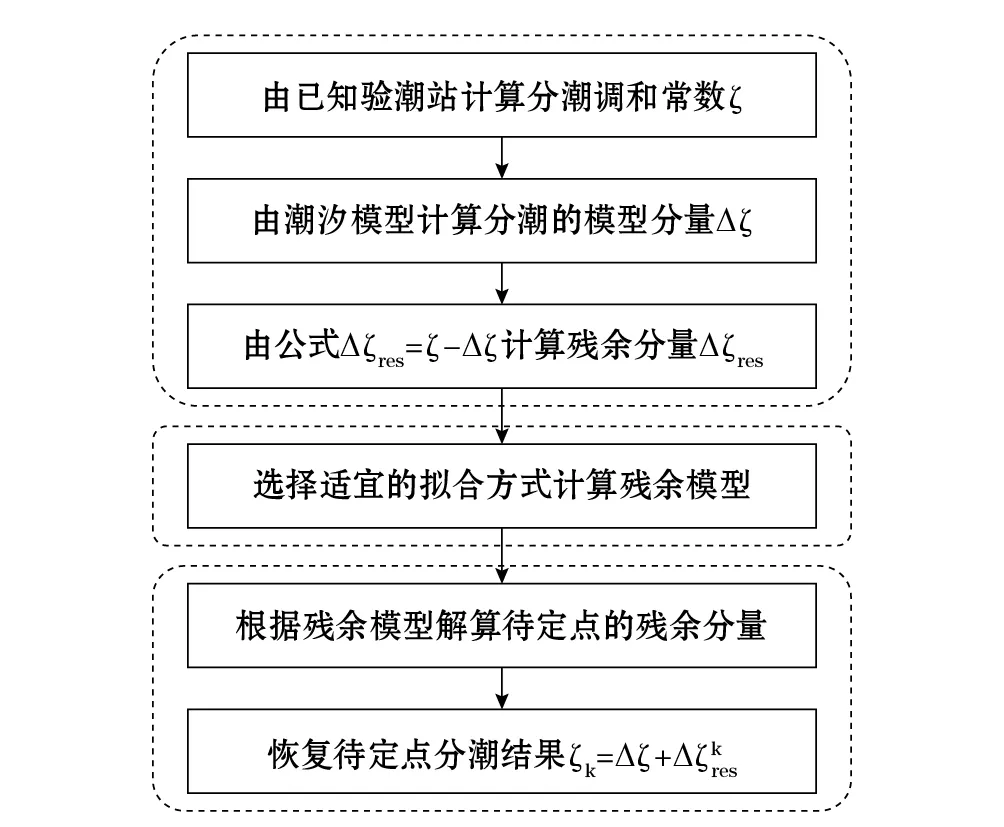
图2　移去-恢复技术流程图Fig.2　Flow chart remove-restore technique

2　结果分析

2.1不同分辨率潮汐模型的精度分析

鉴于已有学者采用的分辨率，本文采用研究区域提取的3 810个正常点的分潮结果，分别建立6′×6′，7.5′×7.5′，30′×30′，1°×1°分辨率的潮汐模型。选取南海海域周边26个长期验潮站数据，对所建模型8个主要分潮(Q1，O1，P1，K1，N2，M2，S2和K2)调和常数进行分析，验潮站位置见图1，对比结果见表2，表中RMS为单分潮综合预报中误差，RSS为8个分潮综合预报误差[20]。

由表2可知，基于T/P系列原始轨道与变轨轨道高度计数据提取的潮汐信息构建的4种不同分辨率的潮汐模型精度不同。当选取分辨率较大时，对于非网格点处的验潮站点，采用一般的插值方式较难反映真实情况，不适合浅水海域；当选取分辨率较小时，较密集的网格点在进行插值时对其邻近点依赖性较大，不适合变化梯度较大的海域。一般而言，潮汐模型的精度是由与选取验潮站对比的结果表示的，选取不同的验潮站其表示精度不同，本文无意提出哪一种分辨率构建的潮汐模型精度更高。由表2结果可知，7.5′×7.5′分辨率的潮汐模型比其他分辨率大小的模型精度要高，其中除O1分潮RMS为10.56 cm外，其余分潮均在10 cm内，因此，本文选取7.5′×7.5′分辨率的潮汐模型进行改进。

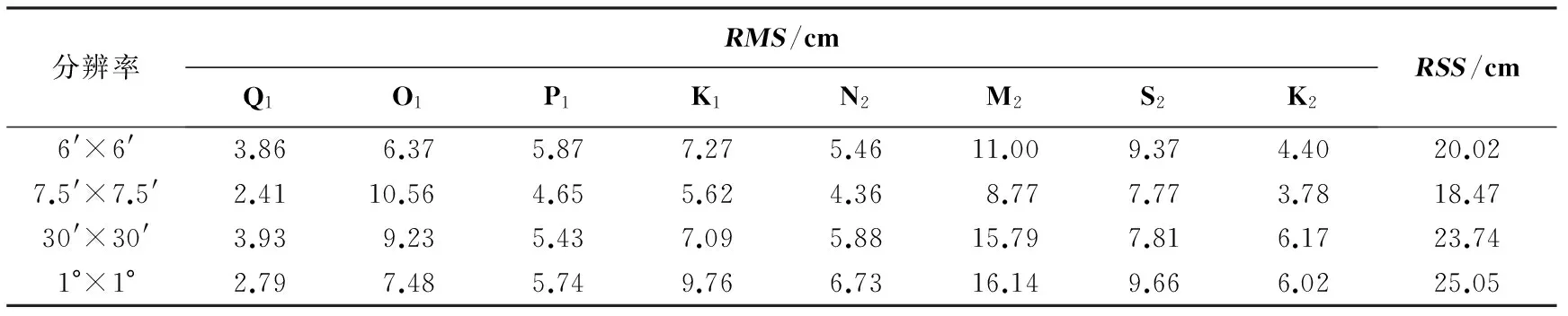
表2　不同分辨率潮汐模型的精度

2.2采用移去-恢复技术的潮汐模型改进

选取两组数据集共101个验潮站实测数据分析结果。第一组数据集来源于夏威夷大学水位数据中心(http:∥uhslc.soest.hawaii.edu/data/download/fd)，数据时间长度均在1 a以上，对其进行调和分析得到各分潮调和常数；第二组数据集来自Fang等[21]，其仅提供了4个最主要分潮(O1，K1，M2和S2)的调和常数，因此，本文仅对这4个最主要分潮进行分析，采用数据集中的验潮站位置见图3。

采用数据集分潮调和常数对2.1节中建立的7.5′×7.5′分辨率的潮汐模型进行精度分析，结果见表3。由于南海浅海海域潮汐规律复杂，较大的变化梯度使得部分验潮站结果与模型值相差较大，因此，表3与表2中4个最主要分潮结果有不同的精度表现。

图3　采用的南海海域验潮站位置图Fig.3　Locations of tide gauge in the South China sea表3　海潮模型与验潮站比较结果Table 3　Comparison between tide model and tidehgauge results

参 数O1K1M2S2RMS/cm14.0215.5817.0013.54RSS/cm30.20

将101个验潮站随机分为10组，每组选取10个验潮站作为待定点，其余91个验潮站为已知点，按照移去-恢复技术操作流程，首先利用已知站点的调和常数，由本文建立的海潮模型内插出这些站点的模型分量，计算差值得到残余分量；然后利用Kriging插值法计算每个网格点的残余分量，构建残余模型；最后基于残余模型采用双线性插值方法计算待定点处残余分量，与模型分量相加得到待定点处的改进值。

逐组采用移去-恢复技术计算待定点分潮的调和常数，本文同时计算了全球海潮模型TPXO7.2，NAO.99b和DTU10在待定点处模型值，各组分潮RMS见图4，改进后模型与全球海潮模型分潮最大值、最小值统计值见表4，对10组数据综合计算结果见表5。

由图4可以看出，改进后模型与3个全球海潮模型的多组数据结果精度相当，其中M2分潮第3组、S2分潮第3组、O1分潮第8组、K1分潮第10组比其余海潮模型要大，主要是因为部分验潮站位于海湾内，其潮波性质比较复杂，当作为待定点时，真实值与改进后的模型值相差较大；当作为已知点时，其残余分量影响了残余模型的精度，故此类验潮站影响了总体精度。

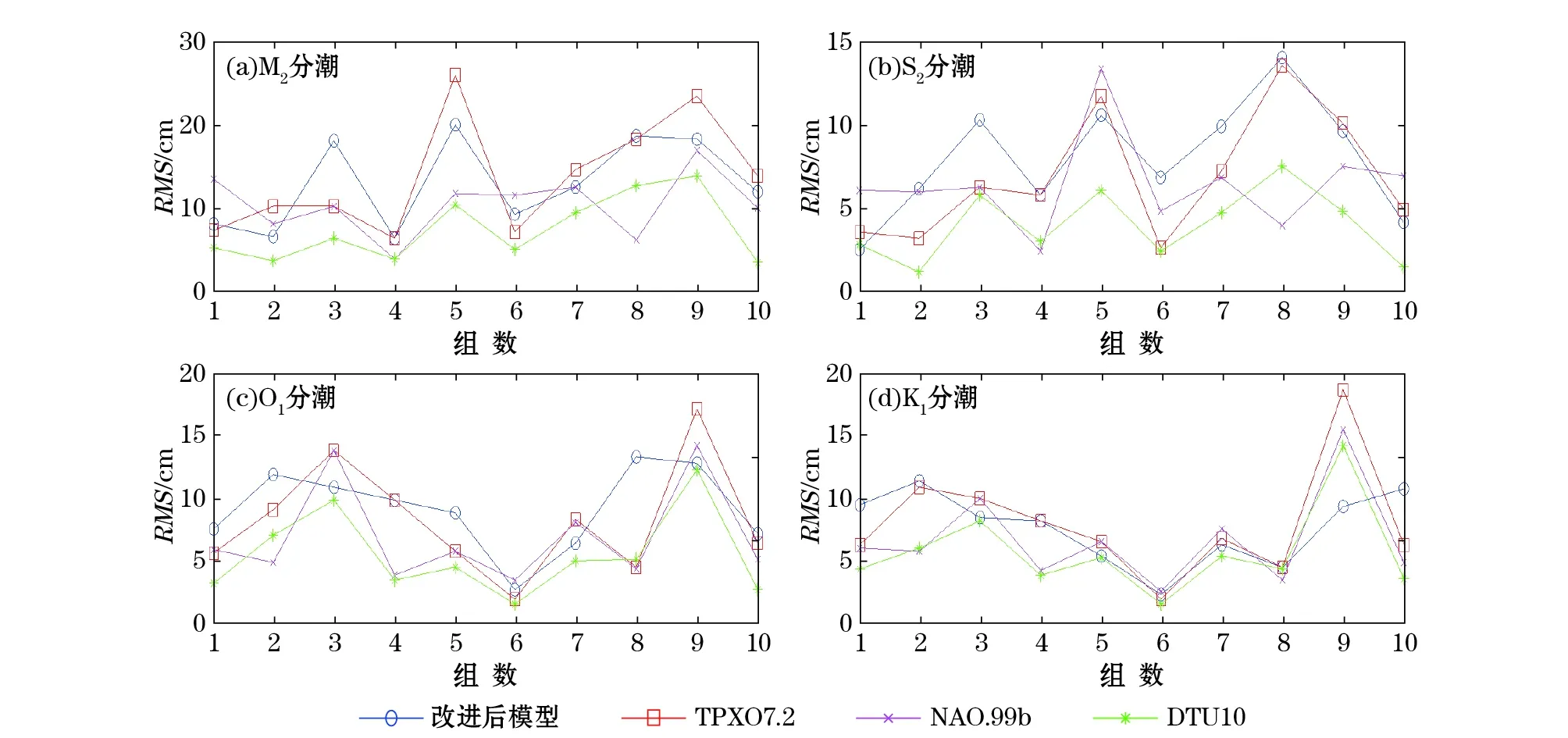
图4　改进后模型与海潮模型分潮结果统计Fig.4　RMS differences between improved tide model and ocean tide models

由表4可以看出，各潮汐模型在每组中分潮的RMS变化较大，主要是因为每组选取不同的验潮站作为已知点，其中存在部分验潮站结果与模型值相差较大，此差值在进行残余分量网格化时，会带动并拉大周围网格点的值，导致周围点与实际不符而影响“恢复”精度，从而在计算待定点残余分量时与实际相差较大。

表4　海潮模型4个最主要分潮RMS最大值、最小值(cm)

通过表5与表3可以看出，4个最主要分潮RMS以及RSS采用移去-恢复技术后的值均有较高程度的提高，改进后模型的O1，S2分潮RMS分别为7.76, 8.51 cm，M2分潮RMS较大为13.86 cm，RSS达到20.32 cm。结果表明，采用移去-恢复技术能够明显改善潮汐模型在浅海海域的精度。

表5　改进后模型与验潮站比对结果

3　结　论

针对多源卫星高度计数据建立的海潮模型在浅海海域精度较低的问题，基于T/P,Jason-1高度计19 a轨道数据进行了南海海域的原始轨道数据的调和分析以及变轨轨道数据的响应分析，分析了建立不同分辨率潮汐模型的精度，结果表明，采用相同的数据源建立不同分辨率的潮汐模型的精度略有差异。提出采用移去-恢复技术应用于潮汐模型浅海海域，并利用南海周边验潮站结果进行试验分析，结果表明，采用移去-恢复技术能够明显改善潮汐模型在浅海海域的精度，这对进一步分析浅海海域潮汐特征具有非常重要的实际意义。

[1]ANDERSEN O B, WOODERORTH P L, FLATHER R A. Intercomparison of recent tide model[J].Journal of Geophysical Research, 1995, 100(C12): 25261-25282.

[2]SHUM C K, WOODERORTH P L, ANDERSON O B, et al. Accuracy assessment of recent ocean tide models[J].Journal of Geophysical Research, 1997, 102(C11): 25173-25194.

[3]WANG Y Q, ZHANG T Y, ZHU X M. Tidal characteristics analysis in the South China Sea by 18.6 years satellite altimetry data[J].Marine Forecasts, 2014, 31(2): 35-40. 王延强,仉天宇,朱学明.基于18.6年卫星高度计资料对南海潮汐的分析与研究[J].海洋预报, 2014, 31(2): 35-40.

[4]SUN J L. Study of improving the precision of coast satellite altimeter and application to South China sea tide model[D].Qingdao:Shandong University of Science and Technology, 2011. 孙佳龙.近海雷达卫星测高数据质量改善及在南海海潮模型中的应用研究[D].青岛:山东科技大学, 2011.

[5]XU J, BAO J Y, ZHANG C Y. Establishment of regional ocean tide model by combination of TOPEX/Poseidon and Geosat/ERM altimeter data[J].Science of Surveying and Mapping, 2006, 33(2): 90-92. 许军,暴景阳,章传银.联合TOPEX/Poseidon与Geosat/ERM测高资料建立区域潮汐模型的研究[J].测绘科学, 2006, 33(2): 90-92.

[6]WANG Y H, FANG G H, WEI Z X, et al. Accuracy assessment of global tide models base on satellite altimetry[J].Advances in Earth Science, 2010, 25(4):353-359. 汪一航,方国洪,魏泽勋,等.基于卫星高度计的全球大洋潮汐模式的准确度评估[J].地球科学进展, 2010, 25(4): 353-359.

[7]GLADKIKH V, TENZER R. A comparison of model estimates of ocean-tide loading displacement in New Zealand[J].Journal of Geodetic Science, 2011, 1(2): 94-113.

[8]GAO X M, WEI Z X, LV X Q, et al. Accuracy assessment of global ocean tide models in the South China Sea[J].Advances in Marine Science, 2014, 32(1): 1-13. 高秀敏,魏泽勋,吕咸青,等.全球大洋潮汐模式在南海的准确度评估[J].海洋科学进展,2014,32(1):1-13.

[9]EGBERT G D, BENNETT A F, FOREMAN M G G. TOPEX/Poseidon tides estimated using a global inverse model[J].Journal of Geophysical Research, 1994, 99(C12): 24821-24852.

[10]EGBERT G D, EROFRVA A S Y. Efficient inverse modeling of barotropic ocean tides[J].Journal of Atmospheric and Technology, 2002, 19(2): 183-204.

[11]MATSUMOTO K, TAKANEZAWA T, OOE M. Ocean tide models developed by assimilating TOPEX/Poseidon altimeter data into hydrodynamical model: A global model and a regional model around Japan[J].Journal of Oceangraphy, 2000, 56(5): 567-581.

[12]CHENG Y C, ANDSERSEN O B. Multimission empirical ocean tide modeling for shallow waters and polar seas[J].Journal of Geophysical Research, 2011, 116(C11), doi:10.1029/2011JC007172.

[13]BAO J Y, XU J. Tide analysis from altimeter data and the establishment and application of tide model[M].Beijing: Surveying and Mapping Press, 2013. 暴景阳,许军.卫星测高数据的潮汐提取与建模应用[M].北京:测绘出版社, 2013.

[14]FANG G H, ZHENG W Z, CHEN Z Y, et al. The analysis and prediction of tide and tidal current[M].Beijing:Ocean Press, 1986. 方国洪,郑文振,陈宗镛,等.潮汐和潮流的分析和预报[M].北京: 海洋出版社, 1986.

[15]LI P L, ZUO J C, LI L, et al. Orthogonalized convolution method for analysis of South China Sea tidal date from TOPEX/Poseidon[J].Oceanologia et Limnologia Sinica, 2002, 33(3): 287-295. 李培良,左军成,李磊,等.南海TOPEX/POSEIDON高度计资料的正交响应法潮汐分析[J].海洋与湖沼, 2002, 33(3): 287-295.

[16]WEI Z Q, WANG G. Determination of quasi-geoid in mainland China using geopotential model and GPS/Leveling data[J].Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 1-5. 魏子卿,王刚.用地球位模型和GPS/水准数据确定我国大陆似大地水准面[J].测绘学报, 2003, 32(1): 1-5.

[17]BAO J Y, XU J. The Accuracy evaluation of harmonic constants for long term tidal stations along the coast of China[J].Hydrographic Surveying and Charting, 2013, 33(1): 1-4. 暴景阳,许军.中国沿岸验潮站潮汐调和常数的精度评估[J].海洋测绘, 2013, 33(1): 1-4.

[18]FU Y G, ZHOU X H, YANG L, et al. Variation trends of major tidal constituents along the northern coast of the South China Sea[J].Hydrographic Surveying and Charting, 2015, 35(1): 14-17. 付延光,周兴华,杨磊,等.中国南海北部潮汐主要分潮的变化趋势分析[J].海洋测绘, 2015, 35(1): 14-17.

[19]WAN X Y, YU J H. Accuracy analysis of the remove-restore process in inverse stockes formula[J].Geomatics and Information Science of Wuhan University, 2012, 37(1): 77-80. 万晓云,于锦海.移去-恢复法在逆Stocks公式计算中的精度分析[J].武汉大学学报(信息科学版), 2012, 37(1): 77-80.

[20]BAO J Y. Study on theories and methods of tidal analysis based on altimetry data[D].Wuhan: Wuhan University, 2002. 暴景阳.基于卫星测高数据的潮汐分析理论与方法研究[D].武汉:武汉大学, 2002.

[21]FANG G H, KWOK Y K, YU K J, et al. Numerical simulation of principal tidal constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand[J].Continental Shelf Research, 1999, 19(7): 845-869.

A Method of Constructing High Precision Tide Model for Shallow Water in the South China Sea

LEI Ning1，2，FU Yan-guang1,2, YANG Long2, ZHOU Xing-hua1,2, YANG Fan-lin1,WANG Zhao-yang1, SUN Wei-kang1

(1.CollegeofGeodesyandGeomatics,ShandongUniversityofScienceandTechnology, Qingdao 266590, China;2.TheFirstInstituteofOceanography,SOA, Qingdao 266061, China)

Aimed to solve the low precision problem in using the altimeter data to establish ocean tide model for shallow water, a method of remove-restore technique is proposed, with 19 years of TOPEX/Poseidon and Jason-1 altimeter data and gauge data being used, for establishing a high precision shallow water tide model. With the mean sea level being the reference surface, we calculated tidal constants for 1 626 normal points by response analysis and 2 184 normal points by harmonic analysis along the altimeter tracks in the South China Sea with 0.1° interval in latitude, and then established grid ocean tide model.RMSdifference andRSSdifference of different solutions of the tidal model are evaluated. Based on tidal constants at gauge stations, the remove-restore technique is applied to improve the tide model precision, and theRMSdifferences of the improved tide model for the four major constituents O1,K1,M2and S2have reached to 7.76 cm, 9.40 cm, 13.86 cm, 8.51 cm, and theRSSdifference has reached to 20.32 cm, showing that the remove-restore technique can improve the precision of the tide model significantly.

satellite altimetry; tidal model; harmonic analysis; response analysis; remove-restore technique

October 12，2015

2015-10-12

中央级公益性科研院所基本科研业务费专项资金资助项目——基于GNSS浮标的卫星高度计定标技术研究(2014G21)；国家海洋局科技司专项业务费项目——开展卫星海洋测绘应用(WX0316005)；国家国际科技合作专项——自主星载高度计海面在轨绝对定标关键技术研究(2014DFA21710)作者简介：雷宁(1982-)，男，湖北天门人，博士研究生，主要从事海平面变化与高度计应用等方面研究.E-mail:hychfio@126.com

杨龙(1979-)，男，山东莱州人，高级工程师，硕士，主要从事海洋测绘理论、技术及应用等方面研究.E-mail:yanglong@fio.org.cn

(王燕编辑)

P731.23

A

1671-6647(2016)03-0370-07

10.3969/j.issn.1671-6647.0000.00.006