基于FxLMS算法的双层隔振系统主动控制研究

揭伟俊,翁雪涛,李超博

(海军工程大学 科研部，武汉　430033)



基于FxLMS算法的双层隔振系统主动控制研究

揭伟俊,翁雪涛,李超博

(海军工程大学 科研部，武汉430033)

摘要：将FxLMS算法应用到双层隔振系统，推导了该算法的实现过程，并进行振动主动控制，分析了步长和阶数对控制效果的影响；建立了双层隔振几何模型，并进行动力学分析，基于Simulink完成双层隔振系统的振动主动控制仿真过程；仿真结果表明：该算法收敛速度快，权值收敛效果好，稳态误差小；运用FxLMS算法，对多频线谱进行综合控制，控制效果良好；在保证系统稳定收敛的情况下，步长和阶数对控制效果的影响明显，合理调节步长和阶数，能明显改进主动控制效果。

关键词：主动控制；FxLMS算法；双层隔振；Simulink 仿真

本文引用格式：揭伟俊,翁雪涛,李超博.基于FxLMS算法的双层隔振系统主动控制研究[J].兵器装备工程学报，2016(6):166-169.

Citationformat:JIEWei-jun,WENGXue-tao,LIChao-bo.ResearchonActiveControlofDouble-LayerVibrationIsolationSystemBasedonFxLMSAlgorithm[J].JournalofOrdnanceEquipmentEngineering,2016(6):166-169.

振动主动控制是通过次级通道的作动器产生主动控制力达到抑制和消除振动的目的，可跟踪振动频率的变化，又可有效抑制低频振动，已成为国内外振动研究的热点问题[1]。而控制算法是振动主动控制的核心，算法的选择直接影响最终的控制结果[2]。目前，应用比较多的是滤波最小均方(FxLMS)自适应算法，该算法对模型参数的变化不敏感，而且能够获得较好的控制效果[3-4]。

目前，已有学者将PID、最优控制和遗传算法应用到双层隔振系统，而关于FxLMS算法在双层隔振系统振动主动控制方面的应用鲜见报道。本文首先介绍FxLMS算法的结构，然后对双层隔振系统进行建模分析，再将FxLMS算法运用到双层隔振系统振动主动控制过程中，对控制过程进行simulink仿真，并对算法的性能进行分析。结果表明应用FxLMS算法的双层隔振系统隔振效果良好[5]。本文对研究复杂激励条件下双层隔振系统的设计、控制及工程应用具有指导意义。

1　FxLMS算法结构

1.1算法的基本结构

FxLMS算法是最小均方(LMS)算法在振动主动控制实际应用中的延伸，利用LMS算法进行自适应前馈控制的原理如图1所示。在自适应控制过程中，W(z)是未知系统H(z) 的最佳估计权值。在振动主动控制中，需要抑制的振动信号d(n)与控制信号y(n)的反向叠加会使得残余振动e(n) 最小，于是达到振动控制的目的[6]。

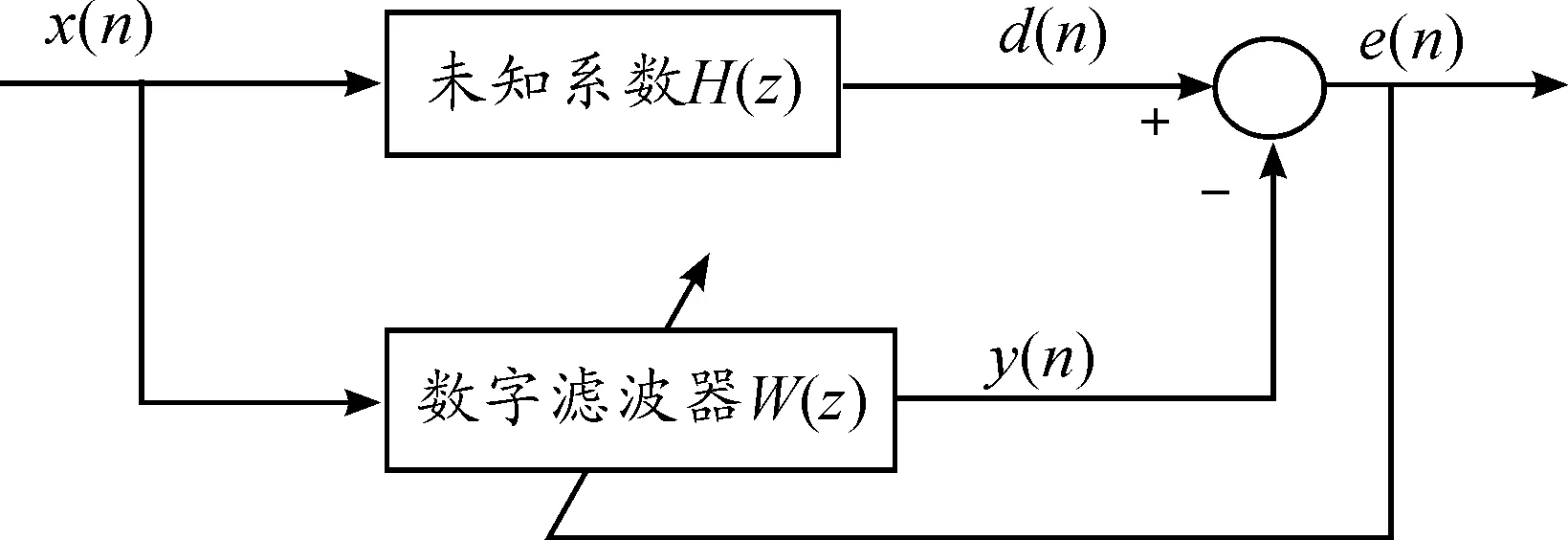
图1　自适应算法

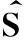
图2　基于滤波x-LMS算法的主动控制系统

1.2算法的推导过程

k时刻的误差信号可以表示为

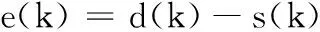
(1)

FIR滤波器的输出控制量为[8]

(2)

在振动主动控制系统中，滤波器输出的控制信号不是所需要的直接控制量[8-10]，它还需要经过误差传感器和控制器之间的次级通道而得到s(k),权向量可表示为

(3)

由表达式

则误差传感器的输出可以写成：

(4)

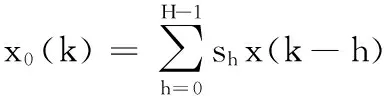
(5)

用误差信号的平方近似均方差

(6)

权值系数矩阵的梯度为

(7)

权值系数的更新公式为

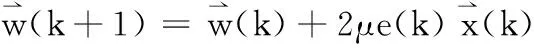
(8)

其中：μ为收敛系数。

2　双层隔振系统建模

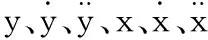
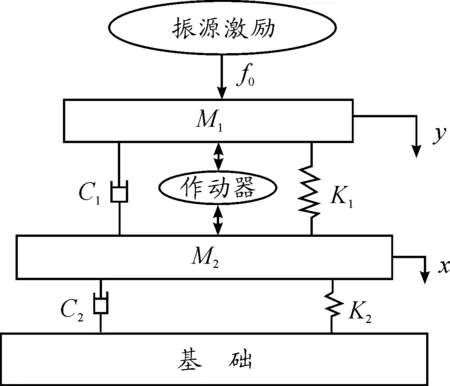
图3　双层隔振系统模型

可建立系统动力学方程为

(8)

对上式进行拉普拉斯变换可得：

(9)

消去变量Y可得：

[M1M2S4+(M1C1+M1C2+M2C1)S3+(M1K1+M1K2+

M2K1+C1C2)S2+(C1K2+C2K1)S+K1K2]X=

(10)

分别令F0S=0、FS=0可获得位移x与主动控制力 f 激励力 f0间的传递函数，具体如下所示：

3　仿真分析

为了对算法模块的有效性进行验证，将S函数建立的FxLMS模块应用到双层隔振系统中进行仿真。以中层隔振平台的加速度作为评价指标，将主动控制与单纯的被动隔振进行对比，系统模型参数如表1所示。

表1　系统模型参数

取激励源为40Hz、100Hz的正弦信号和高斯白噪声信号[11]叠加作为初始振动信号，控制滤波器阶数为300，算法步长μ值为4×10-5，采样时间为10-4。图4为上层平台加速度时域仿真结果，在理想情况下，初始振动信号得到大幅控制， 2.5s左右系统控制效果收敛稳定。图5为控制后残差信号，振动信号几乎完全被抑制，控制误差在1%以内。图6显示权值收敛更新效果良好，权值的个数与滤波器的阶数相等，2.5s后权值收敛稳定。图7为振动信号经主动控制前后频域图，谐波信号在频域内表现为分立的线谱，控制前后线谱的位置没有发生变化，但是振动能量减弱，在40Hz和80Hz处减振效果分别为16.65dB和17.03dB。另外在线谱以外的区域也有一定的减振效果。

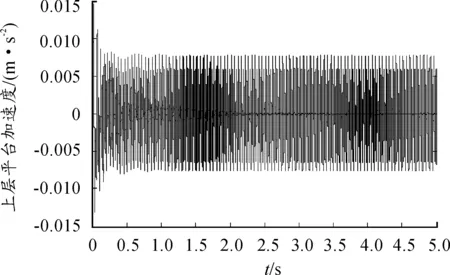
图4　上层平台加速度的时域控制结果

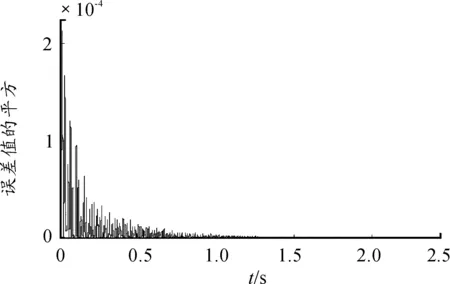
图5　控制后残差信号

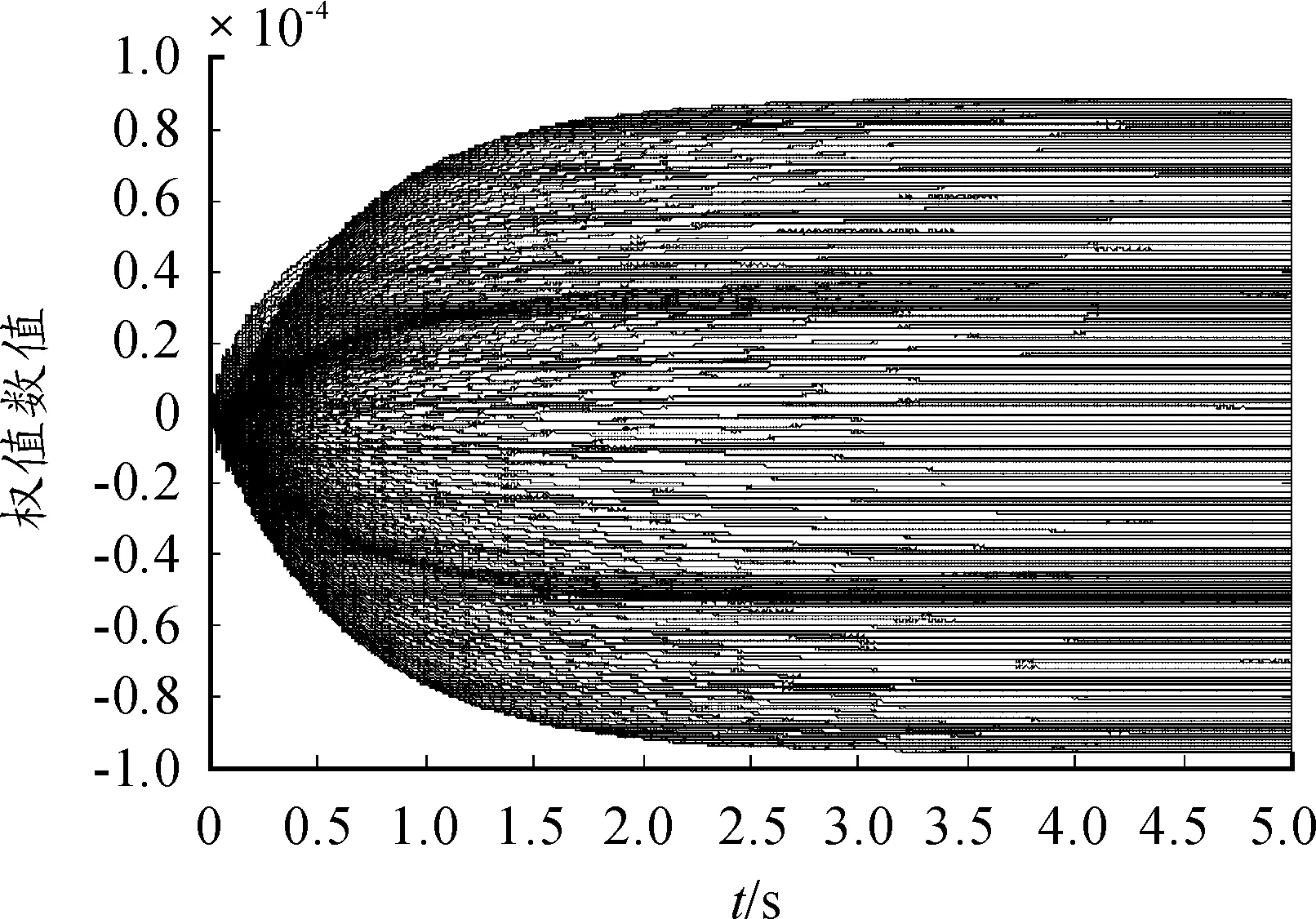
图6　滤波器权值更新

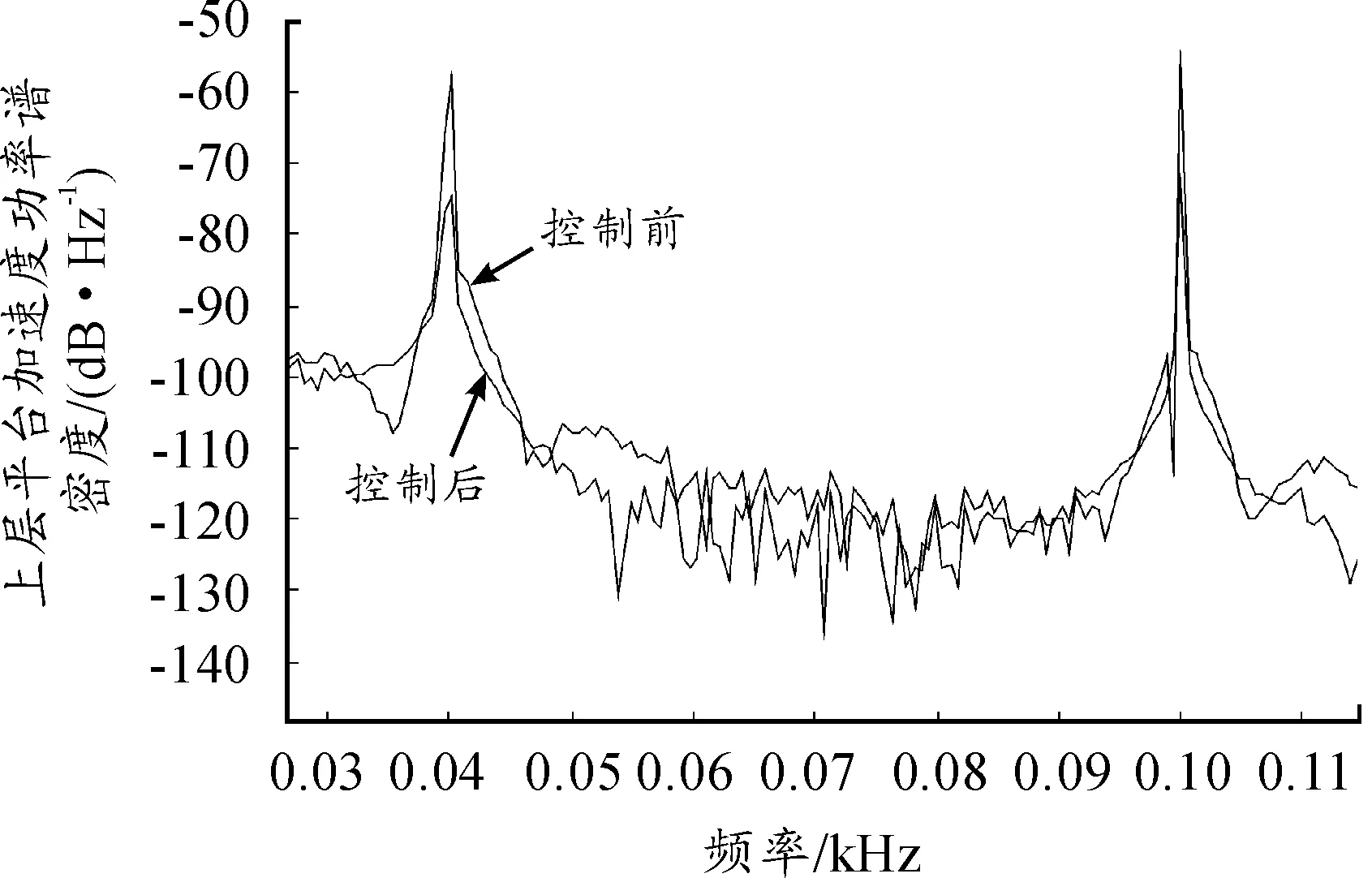
图7　振动信号经主动控制前后频域

4　算法性能分析

在应用FxLMS算法的双层隔振系统中，如果控制系统结构固定，那么主要有两个参数影响其性能：滤波器步长μ和阶数n。FxLMS算法收敛时步长的取值为

(13)

表2　不同控制参数的控制效果

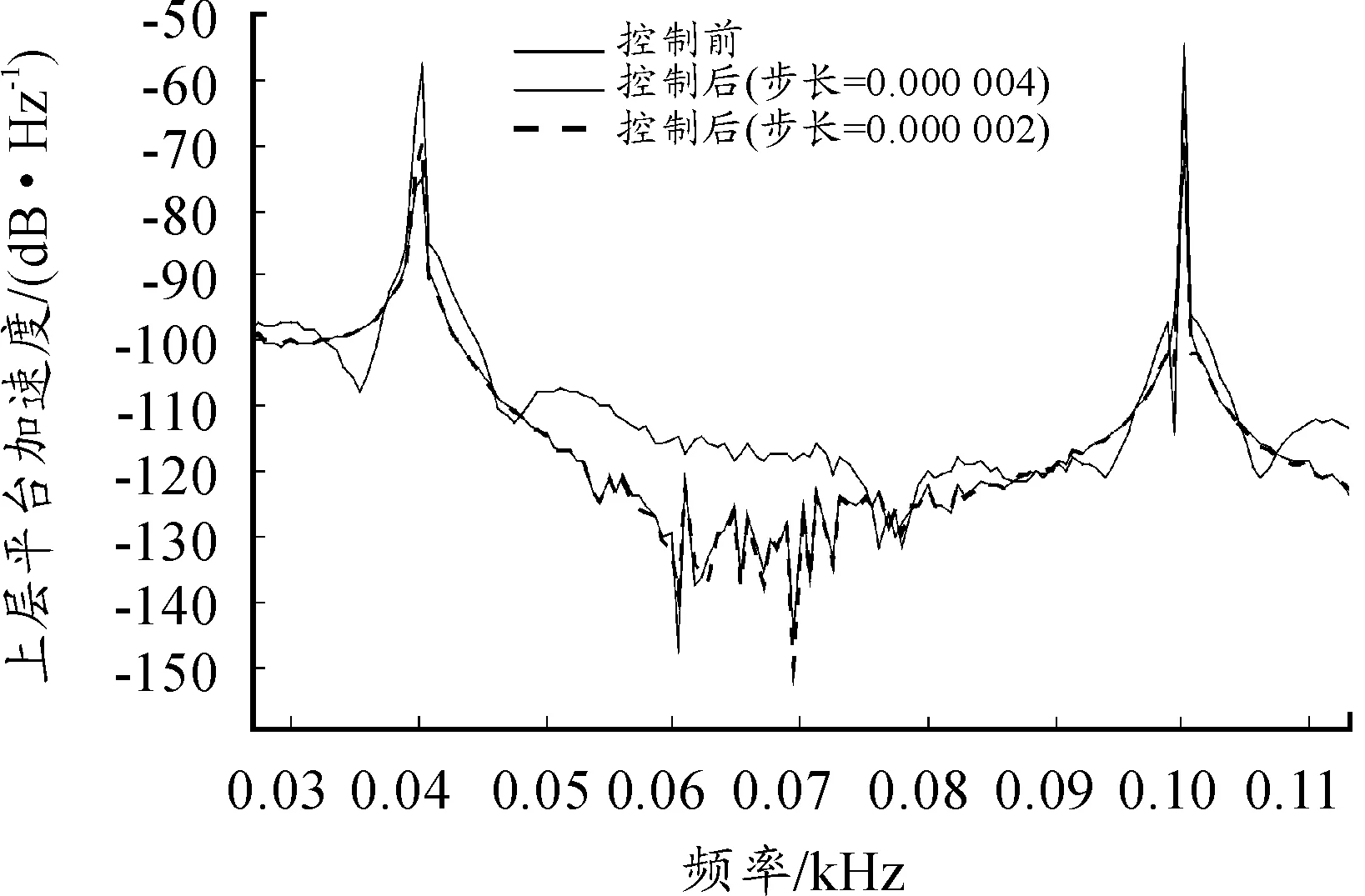
图8　不同步长控制效果对比

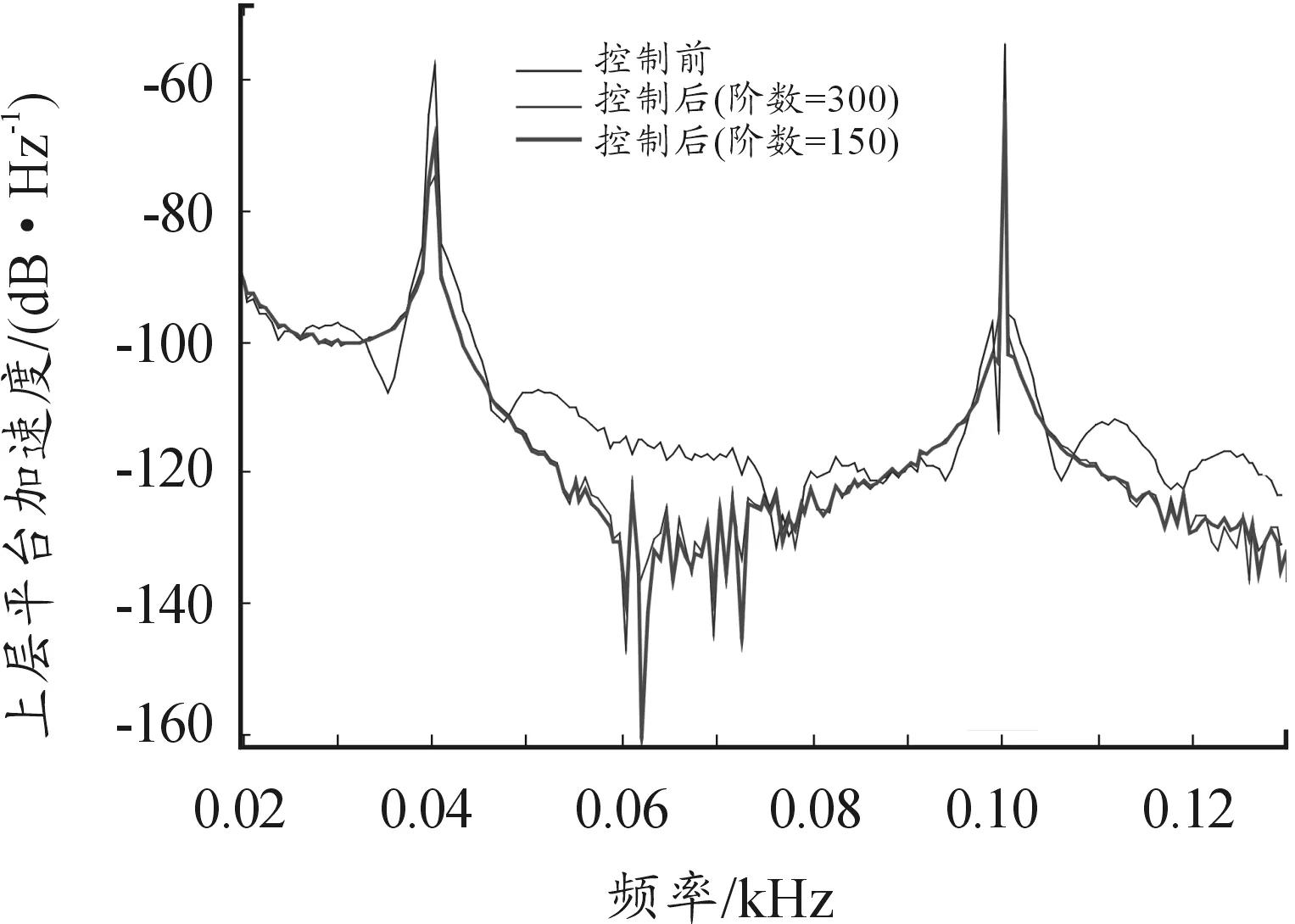
图9　不同阶数控制效果对比

当阶数保持不变，步长变为原来的一半时，40 Hz和100 Hz处控制效果分别减弱为5.59 dB和8.05 dB；当步长保持不变，阶数变为原来的一半时，40 Hz和100 Hz控制效果减弱分别减弱为5.08 dB和8.16 dB。

FxLMS算法的本质是LMS算法，都是梯度下降寻优算法，因此参数对算法性能有着相似影响。在系统稳定的前提下，步长决定了算法的收敛速度和稳态误差，阶数反映了计算的复杂程度[10]。减小步长和阶数，都会使控制效果减弱。前者会减小收敛速度，但减小稳态误差；后者可减小计算的复杂程度。仿真过程分析了算法性能，验证了FxLMS算法的有效性。

仿真结果表明，该算法可在2.5 s内达到收敛稳定，误差保持在1%以内，对加入白噪声的40 Hz和100 Hz线谱的控制效果分别为16.65 dB和17.03 dB。在保证系统稳定的前提下，步长和阶数减小为原来的一半，40 Hz、100 Hz处的控制效果分别减弱为5.59 dB、8.05 dB和5.08 dB、8.16 dB。

5　结论

本文建立了双层隔振模型，将FxLMS算法应用到双层隔振系统，验证了算法的有效性，并对算法性能进行了仿真分析。根据仿真结果，可得到如下结论： FxLMS算法收敛速度快，权值收敛效果好，稳态误差小；算法能够对加入白噪声的多频线谱进行有效控制；在保证系统稳定收敛的情况下，步长和阶数对控制效果的影响明显，合理调节步长和阶数，能明显改进主动控制效果。阶数对于控制算法是预先调节好的，后期可展开对变步长控制过程的研究。

参考文献：

[1]陈玉强.双层隔振系统振动主动控制技术研究[D].哈尔滨:哈尔滨工程大学，2002.

[2]闫政涛，丁少春，楼京俊.振动主动控制技术应用现状与研究进展综述[J].机电信息，2014(9)：73-74.

[3]李以农，张锋，王雷，等.次级通道在线辨识的齿轮啮合振动主动控制[J].振动与冲击.2013，32(6) ：6-12.

[4]肖斌.柴油机双层隔振台架主动隔振技术研究[D].哈尔滨：哈尔滨工程大学，2008.

[5]ZHANG M.Cross-updated Active Noise Control System with Online Secondary PatbModeling [J].IEEE Transactions on Speech and Audio Processing,2001，9(5)：598.

[6]张志谊，王俊芳，周建鹏，等. 基于跟踪滤波的自适应振动控制[J].振动与冲击，2009，28(2)：64-67.

[7]张锋，李以农，丁庆中.FxLMS算法的实现和硬件在环仿真验证[J].重庆大学学报(自然科学版)，2013，36(8) ：26-32.

[8]梁青，段小帅，陈绍青，等.基于滤波x-LMS算法的磁悬浮隔振器控制研究[J].振动与冲击，2010，29(7) ：201-203.

[9]ERIKSSON L J.Use of Rand Noise for Online Transducer Estimate in an Adaptive Attenuation System[J].Acoust Soc Amer,1989,85:797.

[10]贺洪江，王春霞.一种新的LMS自适应滤波算法分析仿真研究[J].传感器与微系统,2012(3)：15-17，21.

(责任编辑杨继森)

doi:10.11809/scbgxb2016.06.039

收稿日期：2015-12-15；修回日期：2016-01-15

基金项目：国家自然科学基金资助(51179197)

作者简介：揭伟俊(1985—)，男，硕士研究生，主要从事军事装备学研究。

中图分类号：O328

文献标识码：A

文章编号：2096-2304(2016)06-0166-04

ResearchonActiveControlofDouble-LayerVibrationIsolationSystemBasedonFxLMSAlgorithm

JIEWei-jun,WENGXue-tao,LIChao-bo

(CollegeofPowerEngineering,NavalUniversityofEngineering,Wuhan430033,China)

Abstract:FxLMS algorithm was applied to the double-layer vibration isolation system. The implementation process of the algorithm was deduced and the active vibration control was acquired at the same time. Then the effect of step size and order to the control effect was analyzed. In order to complete the vibration active control simulation of double-layer vibration isolation system, the double-layer vibration isolation of geometric model was established based on simulink. Simulation results show that: the algorithm has a fast convergence speed, and its weight convergence effect is good and the steady-state error is small; and the control effect of multi frequency spectrum is good by using FxLMS algorithm; and under the case of the stability of the system convergence, the step size and order to the control effect is obvious, the effect can be improved if the step size and order is reasonable.

Key words:active control; FxLMS algorithm; double-layer vibration isolation; Simulink simulation