双层椭圆形药型罩装药射流成形时长短轴比、铝铜铁三种材料的声阻抗和罩间距三因素正交设计研究

孙加肖，尹建平，王志军，唐　琦

(中北大学 机电工程学院，太原　030051)



双层椭圆形药型罩装药射流成形时长短轴比、铝铜铁三种材料的声阻抗和罩间距三因素正交设计研究

孙加肖，尹建平，王志军，唐琦

(中北大学 机电工程学院，太原030051)

摘要：为获得双层椭圆形空心药型罩最佳结构参数，在利用AUTODYN软件对不同方案进行数值模拟分析的基础上，以炸高为2倍口径，射流头部速度和射流断裂前最大长度为考察指标，对影响射流成型的长短轴比、铝铜铁3种材料的声阻抗和罩间距3种结构参数进行设计。结果表明：在这3个因素中，各因素对射流速度影响由主至次的顺序是罩材料声阻抗、长短轴比、罩间距；对射流长度影响由主至次的顺序是长短轴比、罩间距、罩材料声阻抗。外罩材料为声阻抗值较小的铝、长短轴比为1.8、罩间距为2 mm时，双层椭圆形空心药型罩所形成的射流性能最优。

关键词：椭圆形空心药型罩；双层；正交优化；射流速度；射流长度

本文引用格式：孙加肖，尹建平，王志军，等.双层椭圆形药型罩装药射流成形时长短轴比、铝铜铁三种材料的声阻抗和罩间距三因素正交设计研究[J].兵器装备工程学报，2016(6):135-139.

Citationformat:SUNJia-xiao,YINJian-ping,WANGZhi-jun,etal.StudyonOrthogonalDesignoftheAxialRatio,theAcousticImpedanceofAluminum,BronzeandIronandtheSpaceBetweenCoversFormingDoubleOvalHollowLinearJetStream[J].JournalofOrdnanceEquipmentEngineering,2016(6):135-139.

所谓双层药型罩，是指在一个主装药基础上，放置两个药型罩，两层罩之间可以紧密贴合在一起，也可以有间隙；两层罩可以是相同材料，也可以是不同材料，但两层药型罩之间有自由表面，允许两罩发生相对滑移和碰撞[1-4]。正交试验设计方法是一多因素试验方法，具有很高的效率，合理利用该方法能达到事半功倍的效果[5-7]。本文采用正交试验方法对椭圆形罩聚能装药各主要结构参数进行设计，以获得最佳的参数组合方案。

1　正交优化方案设计

设计的聚能装药结构主要采用药型罩断面为椭圆形的装药结构，由主装药和双层药型罩组成，本文没有考虑装药壳体。影响椭圆形罩聚能装药射流成型及侵彻深度的主要因素有炸药参数、药型罩参数(包括声阻抗z/(g/cm2μs)、长短轴比n和罩间距δ等)、药顶高装药口宽以及炸高。本文对结构参数设计时的考察指标为在炸高为2倍口径处射流速度和射流断裂前的最大长度。

根据本文最终确定的影响椭圆形罩聚能射流成型的装药结构因素为长短轴比、铝铜铁三种材料的声阻抗和罩间距以及各因素对应的水平值如表1所示。根据因素数和水平数，选择 L9(34)正交表进行试验方案设计，共进行9次试验，结构参数组合分别为n1-z1-δ1，n1-z2-δ2，n1-z3-δ3，n2-z1-δ2，n2-z2-δ3，n2-z3-δ1，n3-z1-δ3，n3-z2-δ1，n3-z3-δ2。

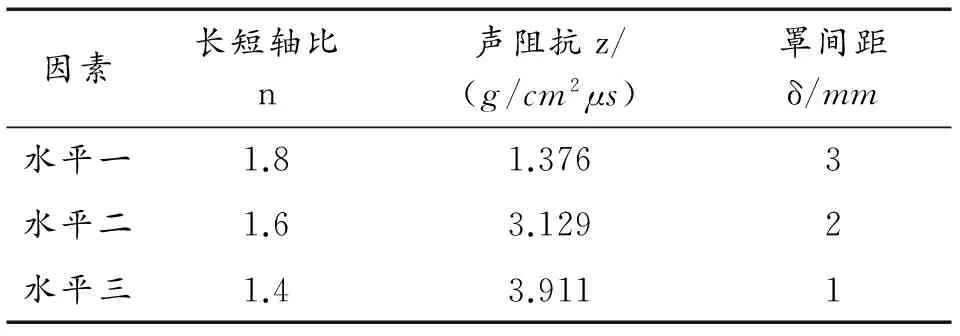
表1　因素和水平

2　有限元模型及计算过程

2.1计算模型及材料模型

计算结构模型如图1所示，其装药口径D为46mm，装药高度H为75mm，内外药型罩壁厚均为1mm，起爆方式采用装药顶端面起爆。

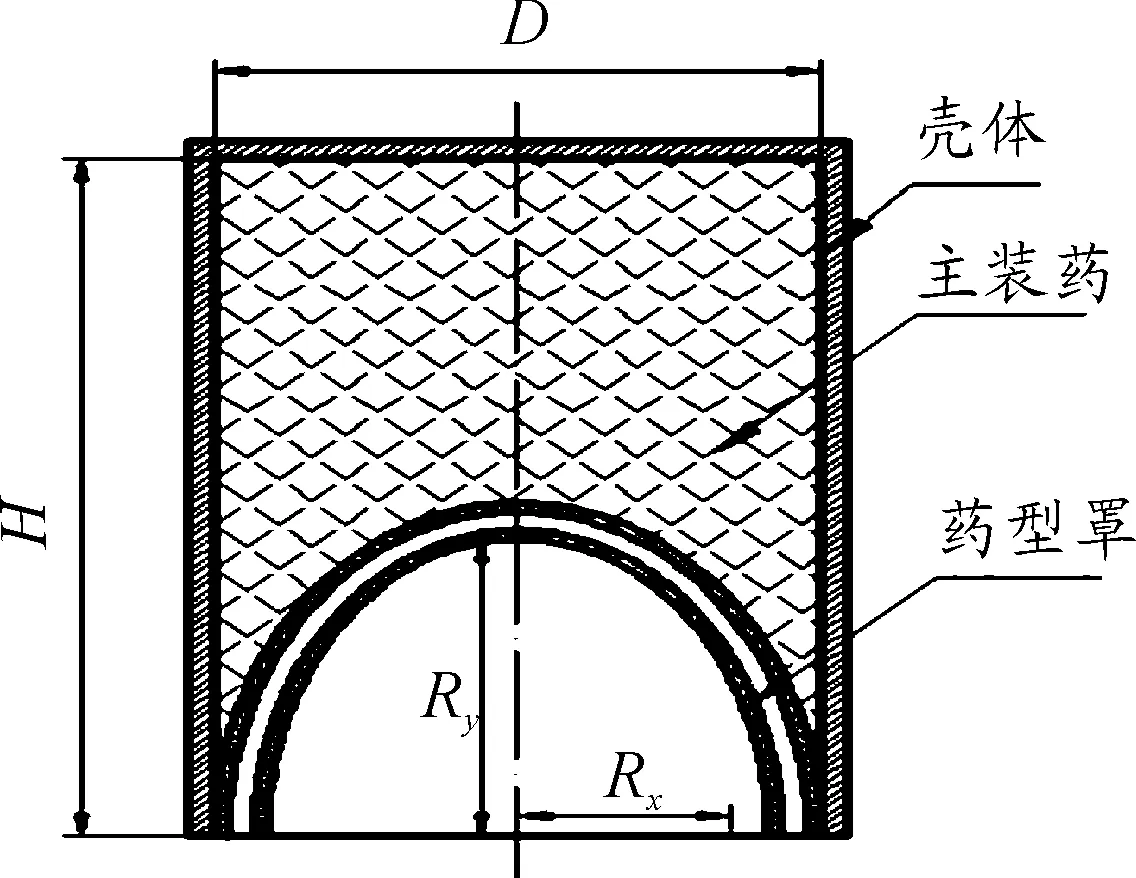
图1　结构模型

使用AUTODYN-2D软件对新型聚能装药结构建立有限元模型。计算模型中没有考虑壳体对射流成型的影响，仅考虑药型罩、主装药和空气三部分，并且均采用Euler单元算法。此外，考虑到装药结构和边界条件的对称性，为节省计算时间，建立二维轴对称有限差分模型；为消除边界效应，在空气边界上添加“Flow-out”边界条件，其有限元模型如图2所示。数值模拟中采用的单位制为mm-mg-μs。

图2　有限元模型

仿真过程中所采用的材料参数均选自AUTODYN-2D程序材料库[9]。空气采用理想气体状态方程描述。炸药采用B炸药，状态方程为JWL。双层椭圆形药型罩内罩均采用紫铜，采用Shock状态方程和Steinberg强度模型来描述药型罩在高应变条件下的变形过程。外罩材料分别选取比较常见的铝、铜和铁。仿真中所用材料模型如表2所示。仿真过程均采用装药底端面起爆。

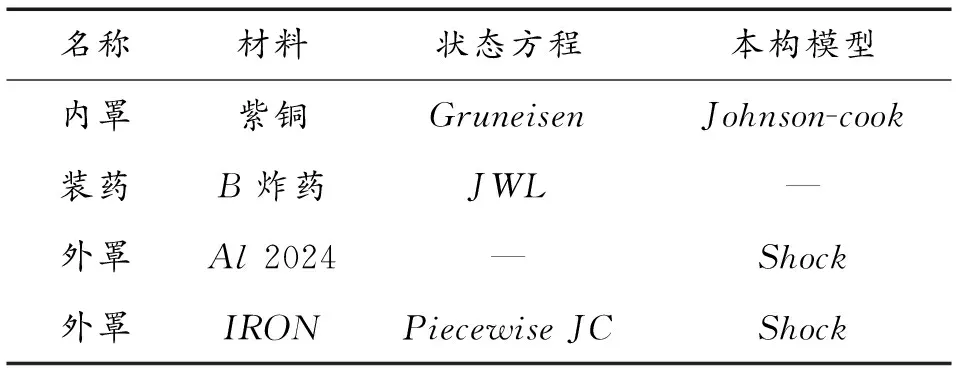
表2　数值模拟中所采用的材料模型

2.2双层椭圆形空心药型罩射流成型过程

当药型罩采用双层椭圆形时，由于拱形结构有极高的径向变形刚度，爆轰压力在药罩中几乎都转化为轴向压力，并且曲率越大的地方分担的轴力也越大，因此长轴比例较大的椭圆罩发生中心壁厚增加的现象越明显，并且与一般的圆锥罩不同，圆锥罩的母线为曲线，爆轰作用力在罩上的压弯点通常发生在圆锥母线中点附近，使得该点以上的圆锥罩变为外形粗大、速度比较低、侵彻能力大大下降的杵体。椭圆罩的压弯点位于椭圆罩的顶端，绝大多数金属材料都在爆轰作用下形成质量分布均匀、具有较大长径比的高速杆式射流侵彻体[10]。

不同时刻下射流的状态如图3所示，此模型中外罩选用铜，长径比选用1.6，罩间距选取2mm。主装药起爆约10μs后，药型罩顶部首先受到爆轰压力的冲量作用，爆轰以其爆速由罩顶向下传播，炸药能量传递给外罩。整个传递过程由罩顶向下依次进行，这种剧烈的爆轰过程驱动外罩和内罩向轴线运动。由于外罩向内压垮的初速度要比内罩的大，使得外罩追上内罩的相应部分并完成汇聚，形成高速射流。由于头尾部速度差的存在，侵彻体在运动中逐渐被拉伸，出现颈缩现象直至被拉断。当t=57μs时，射流开始断裂，此时射流头部速度和长度分别为3 681.7m/s和145.49mm。t=70μs后，射流断裂明显。t=80μs后射流断裂为多段。

图3　典型的射流成型过程

3　数值模拟结果及分析

通过对表1中所列不同方案进行数值计算，得到了在炸高为2倍口径处射流头部速度V和射流断裂前的最大射流长度L，如表3所示。由表3可知，方案1的射流速度最大其值约为4 309.3m/s。方案9的射流长度最长其值约为166.38mm。

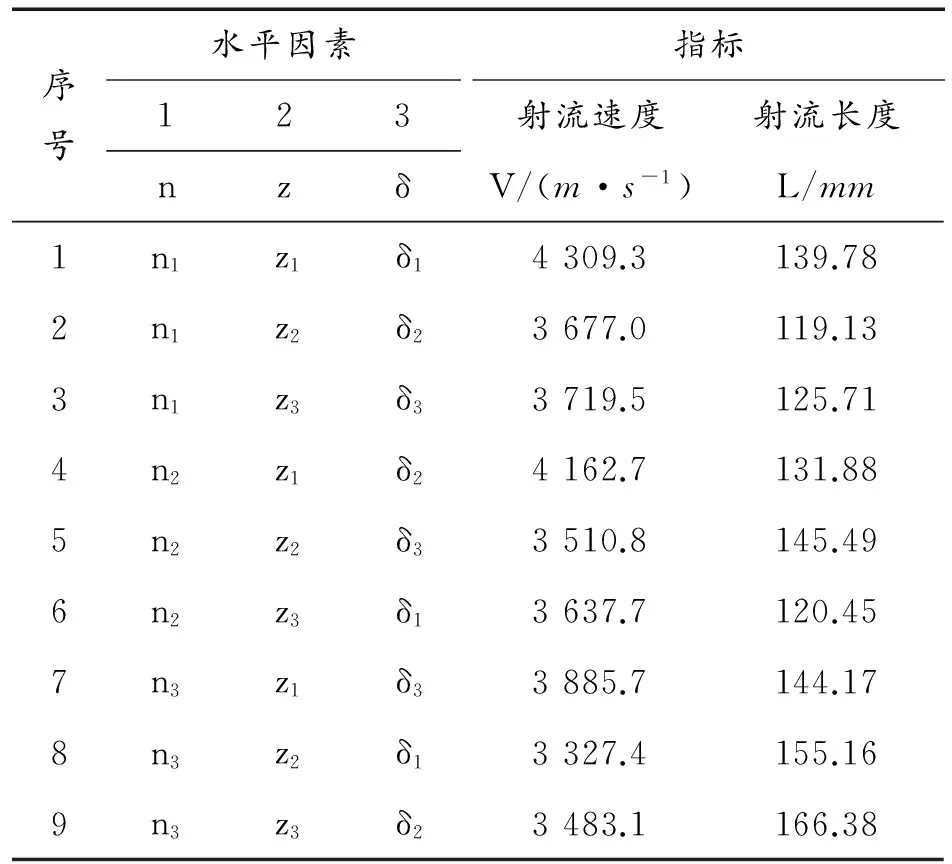
表3　正交优化方案及计算结果

对数值计算所得到的结果进行极差分析，所得极差分析结果如表4所示。由表4的数据可以作出射流速度和射流长度与三因素的关系如图4、图5。

由图4射流速度与三因素关系可知，射流速度随长短轴比n的增加而增加，即在本组方案中n为第一水平1.8时最大。当外罩材料为铝时，即声阻抗为第一水平时，射流速度最大。射流速度随罩间距的增大先增加后减小，即罩间距为第二水平时，射流速度最大。因此，对射流速度而言最佳组合为n1-z1-δ2。

由图5射流长度与三因素关系可知，射流长度随长短轴比n的增大而减小，并且本组方案中n为第三水平1.4时最大。当外罩材料为铁时，即声阻抗为第三水平时，射流长度最大。射流长度随罩间距的增大而增加，且罩间距为第三水平时，射流长度最大。因此，对射流长度而言最佳组合为n3-z3-δ3。

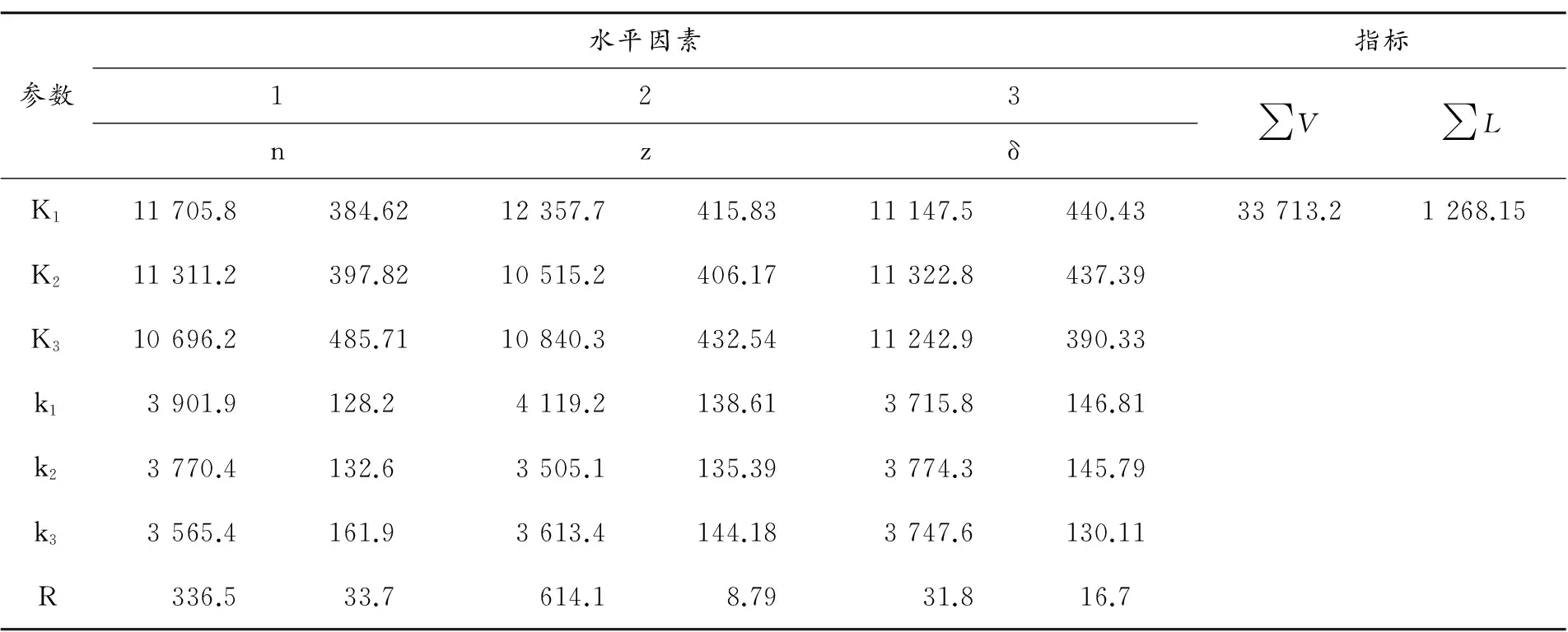
表4　数值模拟结果的极差分析

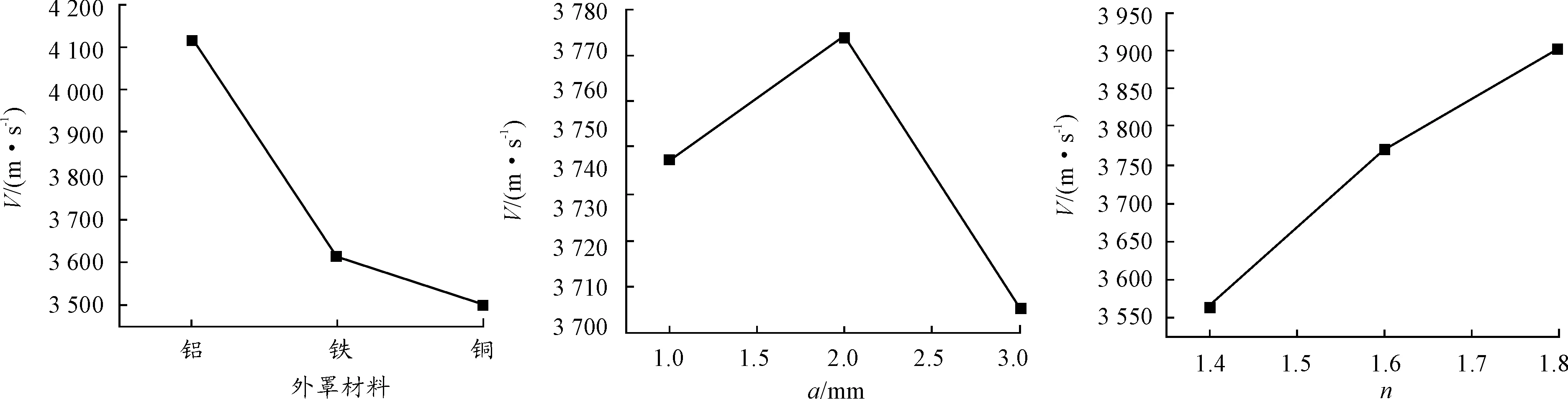
图4　射流速度与三因素关系

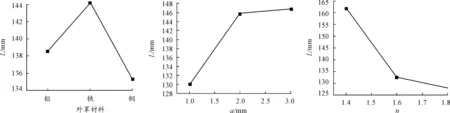
图5　射流长度与三因素关系

各影响因素的变化时所引起的方案指标变化幅度可以通过极差大小来反映，因素的极差越大，该因素对方案指标的影响程度也越大，也就越重要[3]。由表4可知，对射流速度而言，本文所研究的三因素中，声阻抗的影响最大，短轴比次之，罩间距最小，即各因素对长射流速度的影响由主至次的顺序是罩材料声阻抗、长短轴比、罩间距。对射流长度而言，长短轴比的影响最大，罩间距次之，罩材料声阻抗最小，即各因素对射流长度的影响由主至次的顺序是长短轴比、罩间距、外罩材料声阻抗。因此，必须将影响较大的主要因素控制在相对最好的水平上，影响较小的次要因素可以根据实际情况来选择合适的水平。

对射流速度而言，本文所研究的三因素中，罩材料声阻抗对射流速度影响最大，选用铝材料最为合适；长短轴比对射流速度的影响次之，选取长短轴比为1.8较为合适；由于罩间距对射流速度的影响最小，且速度相差最大仅为31.8 m/s，所以n1-z1-δ1同样是一种较好的组合。对射流长度而言，本文所研究的三因素中，长短轴比对射流长度影响最大，故长短轴比选取为1.4；罩间距对射流长度的影响次之，且罩间距为2mm和3mm时长度仅相差1.02 mm，故罩间距为2 mm同样是一种较好的选择；罩材料声阻抗对射流长度的影响最小，考虑到减小外罩材料的密度有利于减小战斗部整体质量，所以外罩材料选取声阻抗较小的铝较好。

综上所述，对射流速度而言，本文所研究的三因素中，获得了2组较好的水平组合，即n1-z1-δ2和n1-z1-δ1。对射流长度而言，获得了3组较好的水平组合，即n3-z3-δ3，n3-z2-δ3和n3-z3-δ1。因为上述九组方案中无n1-z1-δ2，n3-z3-δ3，n3-z2-δ3和n3-z3-δ1，所以对4种水平组合进行建模和计算。5种较优水平组合模拟结果如表5所示。

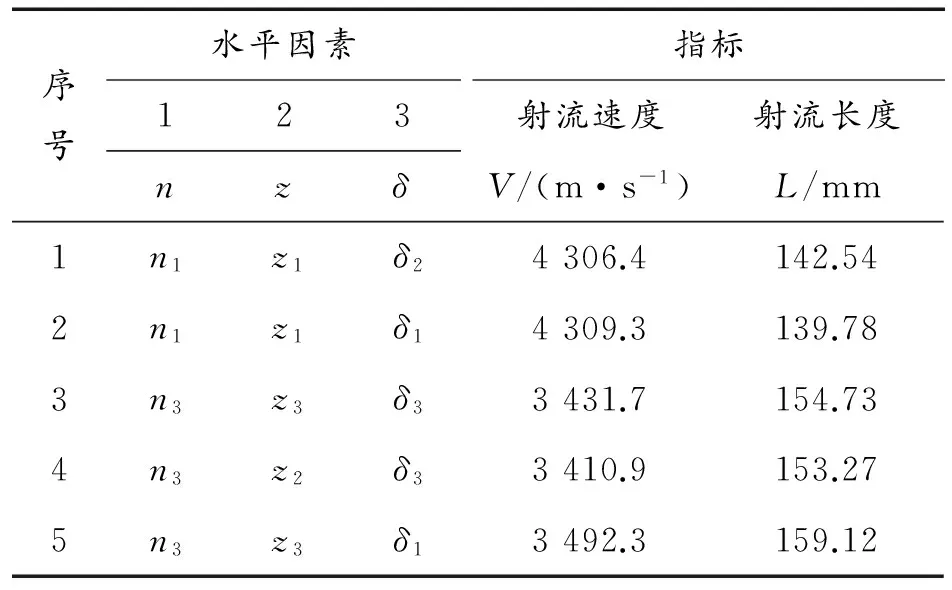
表5　较优水平组合模拟结果

由表4可以看出，对于最大射流速度而言，即前两组方案中，方案1的速度仅比方案2小2.9 m/s，但是射流长度大了2.76 mm，因此选择方案1。对最大射流长度而言，即后三组方案中，方案5的射流长度最长，且对应的射流速度最大，因此选择方案5。

4　侵彻混凝土仿真试验

为了从以上分析中获得的两个方案中的最优方案，通过模拟侵彻混凝土试验，以100 μs时侵彻深度作为最终的判断指标，能够获得最大侵彻深度的方案为最优方案。方案所采用的混凝土为CONC140MPA，炸高为2倍口径，所建有限元模型和侵彻所形成的孔分别如图6、图7所示。

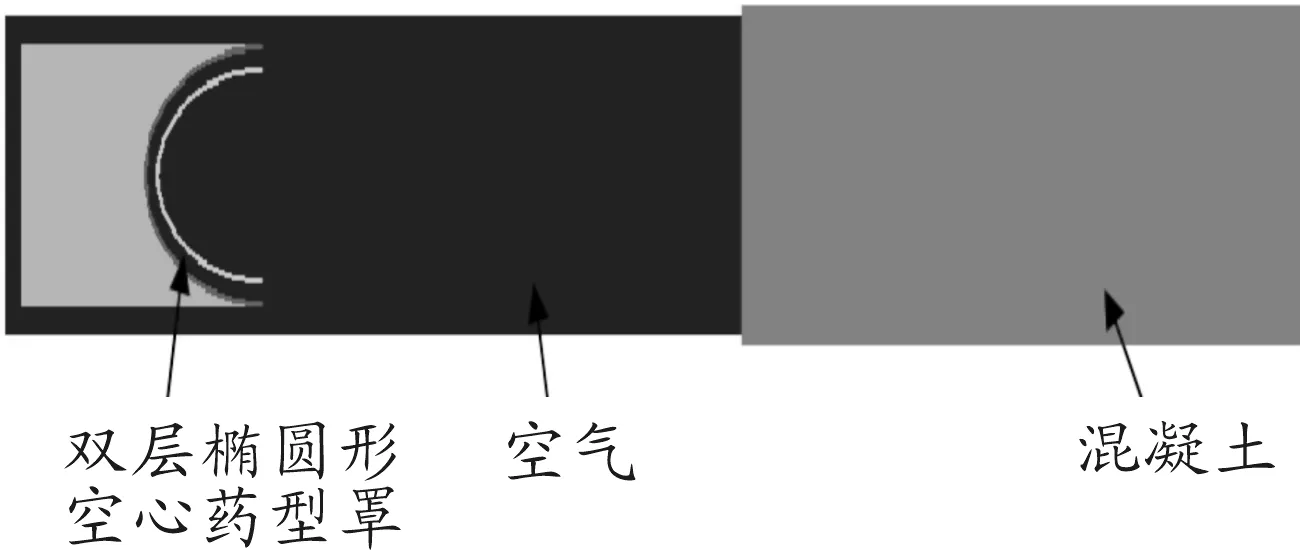
图6　侵彻混凝土试验模型

图7　侵彻所形成孔的效果

通过模拟侵彻混凝土试验，得到方案1和方案5侵彻混凝土所形成孔的深度和直径，如表6所示。

表6　孔的深度和直径

由图7和表6可以看出，在侵彻混凝土试验中，方案1的聚能装药结构所形成的侵彻效果明显优于方案5，即方案1侵彻混凝土形成孔的深度和直径均大于方案5。因此方案1中所采用的结构参数组合较好，即外罩材料选用铝、长短轴比选用1.8、罩间距选用2 mm。

5　结论

1) 运用正交优化方法对双层椭圆形空心药型罩结构参数进行设计，可以得到各因素对射流性能影响的主次关系。本文所研究的因素中，对射流速度的影响由主至次的顺序是罩材料声阻抗、长短轴比、罩间距，对射流长度的影响由主至次的顺序是长短轴比、罩间距、罩材料声阻抗。通过对极差分析表分析可以得出射流速度随长短轴比的增加而增加，随罩间距的增加先增加后减小；射流长度随长短轴比的增大而减小，随罩间距的增大而增加。

2) 通过数值模拟侵彻混凝土试验，最终得出了药型罩结构设计的结构参数，即外罩材料选用铝、长短轴比选用1.8、罩间距选用2 mm。

参考文献:

[1]谭多望,孙承纬.成型装药研究进展[J].爆炸与冲击,2008,28(1):50-56.

[2]孙加肖，尹建平，王志军,等.双层椭圆形空心药型罩射流成型的仿真研究[C]//第十四届全国战斗部与毁伤技术学术交流会.重庆,2015.

[3]CHANG B H,YIN J P,CUI Z P,et al.Numerical Simulation of Modified Low-Density Jet Penetrating Shell Charge[J].International Journal of Simulation Modelling,2015,14(3):426-437.

[4]蒋建伟,杨军,门建兵,等.结构参数对EFP成型影响的数值模拟[J].北京理工大学报,2004,24(11):939-942.

[5]唐密,柏劲松,李平,等.爆炸成型弹丸成型因素的正交设计研究[J].火工品,2006(5):38-41.

[6]郑宇.双层药型罩毁伤元形成机理研究[D].南京：南京理工大学,2008.

[7]武双章,顾文彬,李旭峰.椭圆形罩线型聚能装药结构参数正交优化研究[J].工程爆破,2013,19(3):1-5.

[8]武双章,顾文彬,尼志青,等.起爆方式对截底椭圆形罩LSC射流成型影响的三维数值模拟[J].工程爆破,2015,21(5):47-52.

[9]AUTODTN Theory Manual R4.3[M].Century Dyna-mics Inc,2005.

[10]朱晓茜,朱峰,张咸润.椭球形罩聚能装药侵彻混凝土的数值模拟研究[J].科学技术与工程,2012,32(12):8498-8502.

(责任编辑杨继森)

doi:【化学工程与材料科学】10.11809/scbgxb2016.06.032

收稿日期：2016-01-21；修回日期：2016-02-20

基金项目：国家自然科学基金(11572291);中北大学研究生科技基金(20151201,20151202,20151209)

作者简介：孙加肖(1990—)，男，硕士研究生，主要从事战斗部设计与高效毁伤技术研究。

中图分类号：TJ413

文献标识码：A

文章编号：2096-2304(2016)06-0135-05

StudyonOrthogonalDesignoftheAxialRatio,theAcousticImpedanceofAluminum,BronzeandIronandtheSpaceBetweenCoversFormingDoubleOvalHollowLinearJetStream

SUNJia-xiao,YINJian-ping,WANGZhi-jun,TANGQi

(SchoolofMechatronicEngineering,NorthUniversityofChina,Taiyuan030051,China)

Abstract:In order to obtain the best main structure parameters of the double linear shaped charge with oval cover, the different projects were simulated numerically with AUTODYN-2D program and by using the orthogonal design method, whose inspection index is the maximum length of the pre-broken jet and the head velocity at the burst height which is 2 times of caliber. The effect that influences the structure parameter of axial ratio of jet length, covers distance, material acoustic impedance of jet were optimizedly designed. Studies show that we can know that the primary and secondary relations of jet velocity is material acoustic impedance, axial ratioand distance, and what to jet length is axial ratio, distance and material acoustic impedance. We can obtain that the best jet produced by double linear shaped charge with oval cover to meet the requirement of jet velocity and length, when the material is Aluminum, and the axial ratio is 1.8, and the distance between double layer liner is 2 mm.

Key words:oval hollow linear; double layer; orthogonal optimization; Jet velocity; Jet length