ZnO和ZnS本征点缺陷的理论研究

马昌敏, 刘廷禹, 常秋香, 罗国胤

(上海理工大学理学院, 上海 200093)



ZnO和ZnS本征点缺陷的理论研究

马昌敏, 刘廷禹, 常秋香, 罗国胤

(上海理工大学理学院, 上海 200093)

摘要基于第一性原理和热动力学方法, 通过模拟计算分析了不同温度和分压下ZnS和ZnO晶体本征点缺陷的性质. 振动熵的计算结果表明, 在高温条件下, 振动熵对缺陷形成能的贡献不能忽略. 对比分析2种晶体本征点缺陷随环境条件变化的规律, 结果表明, 2种晶体的主导缺陷均为空位型. 氧空位(VO)在ZnO中更易形成, 富氧和低温条件有利用于ZnO的p型本征掺杂. 而锌空位(VZn)在ZnS中形成能最低, 因此ZnS比ZnO更容易形成p型掺杂. 研究还发现2种晶体的肖特基缺陷都不稳定, 而弗伦克尔缺陷比较稳定. 除ZnS反弗伦克尔缺陷外, 有价态的缺陷对的形成能均比中性缺陷对的形成能低.

关键词密度泛函理论; 点缺陷; 热力学; 氧化锌; 硫化锌

ZnS和ZnO均为锌基Ⅱ-Ⅵ族化合物直接宽带隙半导体, 是非常重要的发光半导体材料, 均包含立方(闪锌矿)和六方(纤锌矿)2种晶体结构.ZnO通常以六方结构存在, 而ZnS通常为立方结构.ZnO的激子束缚能较大(≈60meV), 透明度高, 广泛应用于发光二极管、 荧光材料、 光催化及太阳能光伏材料, 可变电阻及压电材料等领域[1～4].ZnS则在阴极射线管的磷光体、 电致发光器件、 非线性光学器件、 光催化剂及太阳能电池等方面有巨大的应用潜力[5]. 而实现ZnS和ZnO材料的n型和p型稳定掺杂, 是其在该领域应用的关键.

ZnS和ZnO都具有单极性[6], 即: 如果n型掺杂容易,p型掺杂就非常困难, 反之亦然, 这成为其在光电领域应用的瓶颈, 目前已有很多利用共掺控制材料导电类型的报道[7～9]. 但要更好地控制导电类型, 本征点缺陷的深入研究尤为重要. 通过分析本征缺陷的形成来研究施主和受主中心的结构及物理机制, 从而更好地通过掺杂控制材料导电类型.

有关ZnS和ZnO本征点缺陷的研究已有不少报道, 如王洪波等[10]研究了ZnO中主要点缺陷浓度与环境温度和氧分压的热力学关系. 徐彭寿等[11]研究了ZnO本征点缺陷的电子结构, 讨论了其对导电性的影响. 在富氧或富锌条件下, 对ZnO本征缺陷的研究也有报道[12,13].Li和Deng等[14]用第一性原理LDA,LDA+U方法对闪锌矿型ZnS的点缺陷进行了较深入的研究;Morozova和Karetnikov等[15]研究了压强(100～200MPa)和温度(900～1100 ℃)对ZnS的带隙和点缺陷平衡的影响. 关于ZnS高温电导和高温缺陷平衡的研究也有相关研究报道[16,17].

上述研究都局限在特定温度(T)和氧分压或硫分压(pO2或pS2)条件下, 并未对ZnS和ZnO晶体中点缺陷在整个T和pO2或pS2条件下进行全面系统的研究. 也未考虑振动熵对晶体缺陷形成能的影响, 因此, 本文提出在考虑振动熵对缺陷形成能贡献的情况下, 计算得到比较精确的缺陷形成能, 通过研究ZnS和ZnO晶体本征点缺陷的形成能随环境温度T, pO2或pS2和费米能级(EF)的变化关系, 获得外部条件对缺陷稳定性的影响, 为调控晶体n型和p型掺杂提供理论依据. 从而更好地通过掺杂控制材料导电类型.

1计算模型和方法

1.1计算模型

使用VASP软件和交换关联泛函[LDA+U(U=4.7eV)][18,19], 对六方纤锌矿结构ZnO和立方闪锌矿结构ZnS晶体进行了模拟计算. 通过从96个原子的超晶胞中移走或增加原子来模拟缺陷,ZnO晶体结构如图1(A)所示.

图1(A)中a(0.4167, 0.4444, 0.4413)为氧空位及氧被替位的位置,b(0.5833, 0.5556, 0.5000)为锌空位及锌被替位的位置,c(0.5000, 0.3333, 0.5955)为填隙位置.ZnS晶体结构如图1(B)所示.

图1(B)中a(0.5833, 0.6250, 0.3750)为硫空位及硫被替位的位置,b(0.6667, 0.5000, 0.5000)为锌空位及锌被替位的位置,c(0.5000, 0.5000, 0.5000)为填隙位置.Zn的价电子结构为3d4s4p,S的价电子结构为3s3p,O的价电子结构为2s2p、ZnS和ZnO的平面波截断动能分别为360和400eV, 布里渊区的积分采用2×2×2的Monkhorst-Packk点取样求和. 经收敛测试k点和截断动能都已经达到收敛标准(能量差<0.001eV). 结构优化收敛条件: (1) 每个原子的最大能量变化小于0.00001eV; (2) 原子的最大位移小于0.0001nm; (3) 每个原子上受到的最大作用力小于 0.5eV/nm.

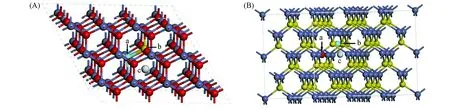
Fig.1　Lattice structures of the ZnO(A) and ZnS(B) crystal

1.2缺陷形成能的计算

点缺陷的吉布斯自由能是关于缺陷种类α、 带电态q、 硫(氧)分压p和温度T的函数, 表达式如下[20～22]:

(1)

式中: Etotal(α, q)和Etotal(perfect)利用VASP计算获得, 分别代表电量为q的α缺陷的超晶胞经弛豫后的总能量和完整晶体的超晶胞经弛豫后的总能量; ni为从超晶胞中移除或添加α原子的数量, 如ni=nZn=1则是超晶胞中有一个Zn空位; μi(T, p)为通过VASP和热力学计算获得的对应原子随温度和分压变化的化学势; EVBM为完整晶体价带顶的能级; EF为指电子相对价带顶的费米能级;ΔV为含缺陷的超晶胞与完整超晶胞间的平均静电势之差; V0为晶体体积, 在计算中是一个常量. 本文用Janotti等描述的校正方式, 对缺陷形成能进行了校正, 具体过程见文献[18], 跃迁能级也进行了校正. 化学势μα(T,p)可以随温度和pS2(或pO2)的变化而变化. 根据Finnis等[23,24]的方法确定硫(氧)的化学势.

本文用GULP软件[25]进行振动熵的计算. 该软件基于Born离子晶格模型, 采用基于核壳模型的半经验势方法计算. 用下式描述距离为r的2个离子间的相互作用:

(2)

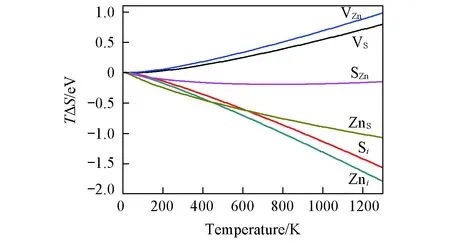
Fig.2　Influence of the vibrational entropy imposed on the intrinsic point defect formation energies in ZnS under different temperatures

利用GULP程序计算完整的和含不同孤立点缺陷晶体的振动熵, 计算公式为

(3)

(4)

式中: Zvib为振动熵的配分函数.

振动熵(TΔS)对缺陷形成能的贡献如图2所示. 计算结果表明, 缺陷的存在改变其周围原子的力场, 从而改变周围原子振动频率引起振动熵的改变, 只有反位硫的振动熵贡献随温度变化比较小, 在高温条件下振动熵贡献总体比较大, 不能忽视.ZnO与ZnS结果相似(此处不再列出).

2结果与讨论

缺陷的形成能可很好地预测晶体的缺陷行为, 因此研究晶体缺陷态在不同环境条件(T, p, EF)下的缺陷形成能非常重要. 图3和图4分别为ZnS和ZnO在不同温度和分压条件下各种缺陷形成能随费米能级变化的关系图. 可以看出,ZnS和ZnO点缺陷的形成能随环境条件变化的基本规律是一致的, 施主型缺陷(VS,Zni,ZnS,VO,ZnO)的形成能是随着pO2或pS2的减少和温度的增加而减少, 但对于受主型缺陷(VZn,Si,SZn,Oi,OZn)变化规律是相反的. 替位型缺陷的形成能变化最快, 所有点缺陷的形成能对温度都比较敏感, 其中一个原因就是振动熵的贡献. 各点缺陷形成能随温度和分压的变化速率在2种晶体中相近, 在T=1300K, 分压p从103Pa到10-10Pa变化时,ZnS中ZnS,VS和Zni缺陷形成能分别减少3.35, 1.62和1.63eV, 而Si,VZn和SZn分别增加1.68, 1.67和3.38eV;ZnO中ZnO,VO和Zni缺陷形成能分别减少3.33, 1.64和1.69eV, 而Oi,VZn和OZn分别增加1.69, 1.73和3.39eV.

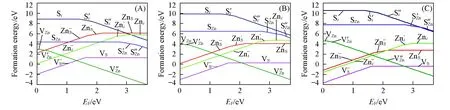
Fig.3　Formation energies of point defects in ZnS as a function of the Fermi level at 1300 KpS2/Pa: (A) 103; (B) 10-5; (C) 10-10.

在ZnO晶体中, 受主缺陷VZn在费米能级处于导带底附近有最低的形成能. 在温度不高的条件下. 在费米能级靠近价带顶区域,VO具有最低的形成能. 但不少研究结果表明, 氧空位的浓度不高[27,28]. 而本文的研究结果表明, 在高温低氧分压条件下,VO具有最低的形成能, 而Oi,OZn和VZn缺陷形成能非常高, 即受主缺陷浓度不高, 不会大量补偿氧空位提供的自由电子, 因此VO是ZnO晶体容易形成n型半导体的重要原因. 有许多研究[29]认为在富锌条件下,Zni缺陷是ZnO本征n型半导体的主要根源, 但是本文结果表明,Zni在所有的条件下都具有非常高的形成能, 它的浓度应该很低, 不能成为ZnO本征n型半导体主要根源.

以往不少研究都认为ZnO是不能进行本征p型掺杂的[8,9]. 本征p型掺杂要求受主(VZn,Oi,OZn)有较低的跃迁能级和形成能, 而且施主缺陷不能对其进行完全有效补偿.VZn为浅受主缺陷, 在富氧低温条件下具有很低的形成能[图4(A)], 与此同时施主缺陷具有较高的形成能, 因此, 本文预测在富氧和低温条件下有利于ZnO的p型本征掺杂.

Fig.4　Formation energies of point defects in ZnO as a function of the Fermi level (A)—(C) T=300 K, pO2=103, 10-5, 10-10 Pa; (D)—(F) T=1300 K, pO2=103, 10-5, 10-10 Pa.

在ZnS晶体中, 本征点缺陷形成能的变化规律与ZnO相似.ZnO晶体在一些特定条件下, 整个EF区域都只有VO的形成能最低, 也就是阴离子空位在ZnO中容易形成, 而ZnS晶体中大多数条件下VZn的形成能最低, 并且在ZnS中的VZn的跃迁能级更低, 因此ZnS比ZnO更容易进行本征p型掺杂, 这与富硫条件下ZnS应是弱p型半导体的结论[30]相一致.

局部电中性是晶体稳定存在的基本要求, 因此, 带电点缺陷在晶体中是很难孤立存在的, 通常是以电中性的缺陷对形式存在, 因此, 研究弗仑克尔缺陷(阳离子空位与阳离子填隙形成电中性的缺陷对)、 反弗仑克尔缺陷(阴离子空位与阴离子填隙形成电中性的缺陷对)和肖特基缺陷(阳离子空位与阴离子空位形成电中性的缺陷对)等缺陷对的形成能是很有必要, 计算公式如下:

(5)

(6)

(7)

式中:Vα为硫空位或氧空位(VS或VO); αi为硫填隙或氧填隙(Si和Oi); μα为硫或氧的化学势(μS或μO).

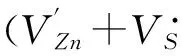
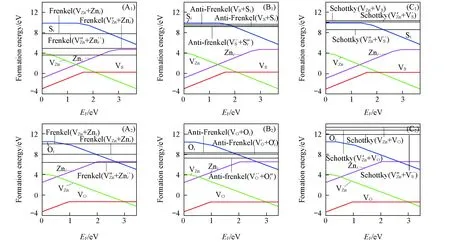
Fig.5　Calculated formation energies of intrinsic point defect complexes (A1, A2) Frenkel; (B1, B2) anti-Frenkel; (C1, C2) schottky pairs. (A1—C1) ZnS; (A2—C2) ZnO.

综上所述,ZnS和ZnO2种晶体的主导缺陷都是空位型. 施主型缺陷(VS,Zni,ZnS,VO,ZnO)的形成能是随着pO2或pS2的减少和T的增加而减少. 对于受主型缺陷(VZn,Si,SZn,Oi,OZn)变化规律是相反的, 并且替位型缺陷的形成能变化最快. 在ZnO中容易形成阴离子空位, 因此,ZnO中VO能够提供n型掺杂, 在富氧和低温条件下有利于ZnO的p型本征掺杂. 而ZnS中, 大多数条件下VZn的形成能最低, 因此ZnS比ZnO更容易进行本征p型掺杂. 阴离子空位(VS和VO)在高温, 低pO2或pS2条件下容易形成, 而阳离子空位VZn在富硫条件下容易形成. 2种晶体中肖特基缺陷都不稳定, 而弗伦克尔缺陷比较稳定, 并且除了ZnS反弗伦克尔缺陷以外, 由带电点缺陷组合成缺陷对的形成能比电中性的低.ZnO的弗伦克尔缺陷和肖特基缺陷的形成能都比ZnS的高, 而反弗伦克尔缺陷是ZnS比ZnO高. 对3种缺陷对而言, 弗伦克尔缺陷不同价态之间结合能量差异最大.

参考文献

[1]TribouletR., Proc. SPIE, 2001, 4412, 1—8

[2]WangZ.L., J. Phys.: Condens. Matter., 2004, 16, 829—858

[3]LingJ.,CongR.M., Acta Chim. Sinica, 2008, 66(18), 2070—2074(凌剑, 丛日敏. 化学学报, 2008, 66(18), 2070—2074)

[4]SongJ.Z.,HeY.,ZhuD.,ChenJ.,PeiC.L.,WangJ.A., Acta Phys.-Chim. Sin., 2011, 27(5), 1207—1213(宋继中, 贺英, 朱棣, 陈杰, 裴昌龙, 王均安. 物理化学学报, 2011, 27(5), 1207—1213)

[5]XinD.S.,ShiJ.X.,PangQ., Acta Scientiarum Naturalium Universitatis Sunyatseni, 2003, 42(6), 125—127(邢德松, 石建新, 庞起. 中山大学学报(自然科学版), 2003, 42(6), 125—127)

[6]YanY.F.,LiJ.B.,WeiS.H.,Al-JassimM.M., Phys. Rev. Lett., 2007, 98, 1—4

[7]DengB.,LuoM.,DongH.N., Electronic Quality, 2012, 1, 8—10(邓博, 罗敏, 董会宁. 电子质量, 2012, 1, 8—10)

[8]ChenL.J.,LiW.X.,DaiJ.F.,WangQ., Acta Phys. Sin., 2014, 63(19), 196101(陈立晶, 李维学, 戴剑锋, 王青. 物理学报, 2014, 63(19), 196101)

[9]YangT.Y.,KongC.Y.,RuanH.B.,QinG.P.,LiW.J.,LiangW.W.,MengX.D.,ZhaoY.H.,FangL.,CuiY.T., Acta Phys. Sin., 2012, 61, 168101(杨天勇, 孔春阳, 阮海波, 秦国平, 李万俊, 梁薇薇, 孟祥丹, 赵永红, 方亮, 崔玉婷. 物理学报, 2012, 61, 168101)

[10]WangH.B.,ZhangJ.W.,YangX.D.,LiuZ.L.,XuQ.A.,HouX., Acta Phys. Sin., 2005, 54(6), 2893—2898(王洪波, 张景文, 杨晓东, 刘振玲, 徐庆安, 侯洵. 物理学报, 2005, 54(6), 2893—2898)

[11]XuP.S.,ShunY.M.,ShiC.S.,XuF.Q.,PangH.B., Science China A, 2001, 31(4), 358—365(徐彭寿, 孙玉明, 施朝淑, 徐法强, 潘海斌. 中国科学,A辑, 2001, 31(4), 358—365)

[12]KohanA.F.,CederG.,MorganD., Phys. Rev. B, 1995, 61, 15019—15027

[13]ObaF.,ChoiM.,TogoA.,TanakaI., Sci. Technol. Adv. Mater., 2011, 12, 034302

[14]LiP.,DengS.H.,ZhangL.,LiuG.H.,YuJ.Y., Chem. Phys. Lett., 2012, 531, 75—79

[15]MorozovaN.K.,KaretnikovI.A.,GolubK.V.,GavrishchukE.M.,YashinaE.V.,PlotnichenkoV.G.,GalstyanV.G., Inorg. Mater., 2004, 40(11), 1138—1145

[16]LottK.,ShinkarenkoS.,TurnL.,NirkT.,OpikA.,KallavusU.,GorokhovaE.,GrebennikA.,VishnjakovA., Phys. B, 2009, 404, 5006—5008

[17]LottK.,TurnL.,VolobujevaO.,LeskelaM., Phys. B, 2001, 949, 308—310

[18]AndersonJ.,VandeWalleC.G., Phys. Rev. B, 2007, 76, 165202

[19]LiP.,DengS.H.,ZhangL.,YuJ., Chem. Phys. Lett., 2012, 531, 75—79

[20]KohanA.F.,CederG.,MorganD.,VandeWalleC.G., Phys. Rev. B, 2000, 61, 15019

[21]VandeWalleC.G.,NeugebauerJ., J. Appl. Phys., 2004, 95, 3851—3879

[22]ZhangS.B.,NorthrupS.B., Phys. Rev. B, 1991, 67(17), 2339—2346

[23]BatyrevI.G.,AlaviA.,FinnisM.W., Phys. Rev. B, 2000, 62(7), 4698—4707

[24]FinnisM.W.,LozovoiA.Y.,AlaviA., Ann. Rev. Mat. Res., 2005, 35, 167—179

[25]GaleJ.D., Chem. J. Soc. Faraday Trans., 1997, 93, 629—637

[26]ObaF.,AdachiH., J. Mater. Res., 2000, 15(10), 2168—2175

[27]JanottiA.,VandeWalleC.G., J. Cryst. Growth, 2006, 287, 58—65

[28]SantanaJ.A.,KrogelJ.T.,KimJ.,PaulR.C.K.,ReboredoF.A., Cond. Mat. Mtrl. Sci., 2014, 12, 23—30

[29]ZhangS.B.,WeiS.H.,ZungerA., Phys. Rev. B, 2001, 63, 075205

[30]GaiY.,LiJ.,YaoB.,XiaJ.B., J. Appl. Phys., 2009, 105, 113704

[31]HeJ.,BeheraR.K.,FinnisM.W., Acta Mat., 2007, 55, 4325—4337

(Ed.:Y,Z)

†SupportedbytheFoundationofHujiang,China(No.B14004).

doi:10.7503/cjcu20150973

收稿日期:2015-12-23. 网络出版日期: 2016-04-20.

基金项目：沪江基金项目(批准号: B14004)资助.

中图分类号O641

文献标志码A

TheoreticalStudiesontheIntrinsicDefectsinZnOandZnSCrystal†

MAChangmin,LIUTingyu*,CHANGQiuxiang,LUOGuoyin

(College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China)

AbstractThe stability of the intrinsic point defects in ZnS and ZnO crystal over a range of temperature and the partial pressure pS2and pO2was studied with the approach that integrates first-principles, thermodynamic calculations and the contributions of vibrational entropy. The results indicate that the contribution of the vibrational entropy to the defect formation energy could not be ignored under high temperature condition. The vacancy-type defects are the predominant intrinsic point defects in ZnS and ZnO crystal. The anion vacancy(VO) forms more easily in ZnO crystal, however, the VZnhas the lowest formation energy in ZnS under most conditions. Therefore, ZnS crystal is easier to perform p-type doping than ZnO crystal. The defect formation energies of the complex point defect, including Frenkel pairs, anti-Frenkel pairs and Schottky pairs, were calculated to predict relative stability. The calculated results show that the Schottky defect pairs are the most unstable, the Frenkel defect pairs are the most stable. Except anti-Frenkel pairs in ZnS, the combinations of charged defects produce lower defect formation energies than combinations of neutral defects.

KeywordsDensity functional theory(DFT); Point defect; Thermodynamics; ZnO; ZnS

联系人简介: 刘廷禹, 男, 博士, 教授, 主要从事晶体点缺陷研究.E-mail:liutyyxj@163.com