Weakly r-Clean Rings

MENG Wenjing, CHEN Huanyin

(College of Science, Hangzhou Normal University,Hangzhou 310036, China)



Weakly r-Clean Rings

MENG Wenjing, CHEN Huanyin

(College of Science, Hangzhou Normal University,Hangzhou 310036, China)

Abstract：This paper defines weakly r-clean rings. A ring R is a weakly r-clean ring if every element x∈R can be written in the form x=r+e or x=r-e where r∈Reg(R) and e∈Id(R). Firstly, various conditions under which a weakly r-clean ring is weakly clean are investigated. Further, some properties of weakly r-clean rings are explored. These extend the corresponding results on r-clean rings.

Key words：clean ring; regular element; idempotent; r-clean ring; weakly r-clean ring

Article ID: 1674-232X(2016)04-0394-07

1Introduction

Through this paper,Rdenotes an associative ring with identity.Zdenotes the ring of integers and for a positive integern,Znis the ring of integers modulon. We writeId(R),Reg(R) andU(R) for the set of idempotents ofR, the set of regular elements ofRand the set of units ofRrespectively.

A ringRis clean if for eachx∈Rcan be written in the formx=u+ewhereu∈U(R) ande∈Id(R). Such type of rings were extensively studied by many authors (see[1-4]). In [1] , the author called a ringRis a weakly clean ring if every element is a sum or a difference of a unit and an idempotent. We know that an elementrin a ringRis said to be regular ifr=ryrfor somey∈R. The ringRis regular if every element inRis regular. Following [2] , a ringRis ar-clean ring if every elementx∈Rcan be written in the formx=r+ewherer∈Reg(R) ande∈Id(R).

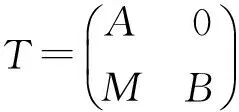
2The Main Results

Definition1AringRisaweaklyr-cleanringifeveryelementx∈Rcanbewrittenasx=r+eorx=r-ewherer∈Reg(R)ande∈Id(R).

Example1RegularringsandBooleanringsareweaklyr-clean.

Clearly,weaklycleanringsareweaklyr-cleanrings.LetRbeacommutativeringwithexactlytwomaximalidealsandsupposethat2∈U(R).ThenRisweaklycleanring[1,Proposition2.6].AndthereforeRisaweaklyr-cleanring.Butingeneral,weaklyr-cleanringsmaybenotweaklyclean.Inthenext,weinvestigatesomeconditionsunderwhichaweaklyr-cleanringisweaklyclean.

Lemma1LetRbeaweaklycleanringand2isinvertibleinR,thenRisa3-goodring.

□

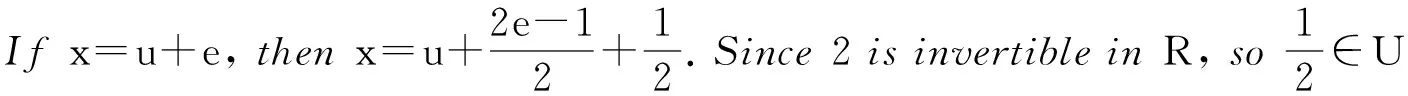
Example2LetFbeafieldwithchar(F)≠2, A=F[[x] ]andKbethefieldoffractionofA.AlltheidealsofAaregeneratedbypowerofx,denotedby(xn).Define:

R={r∈End(AF)|thereexistsq∈Kandapositiveintegern,

withr(a)=qaforalla∈(xn)}.

By[2,Example1] , RisaregularringwhichisnotdirectlyfiniteandRisnotgeneratedbyitsunits.SoeveryelementofRisnotasumofunits,andsincechar(F)≠2, 2isinvertibleinR.AlsosinceRisregularthusRisweaklyr-clean.ButRisnotweaklyclean,becausebyLemma1,weaklycleanringis3-goodring,thuseveryelementinRisgeneratedbyitsunitswhichisacontradiction.

Theorem1LetRbeaweaklyr-cleanring.IfRhasnonontrivialidempotents,thenRisweaklyclean.

ProofFirstly,weprovethattheringRisdirectlyfinite.Ifab=1,(ba)2=b(ab)a=ba,thenba=1orba=0.Ifba=0,thenb(ab)=(ba)b=0,soab=0,whichisacontradition.ThereforeRisdirectlyfinite.SinceRisweaklyr-clean,thenx=r+eorx=r-ewherer∈Reg(R)ande∈Id(R).

CaseI,ifr=0,thenx=eorx=-e.Ande=(2e-1)+(1-e)where2e-1∈U(R)and1-e∈Id(R), -e=-1+(1-e)where-1∈U(R)and1-e∈Id(R).HenceRiscleanringandclearlyRisweaklycleanring.

CaseII,ifr≠0,thenthereexistsy∈Rsuchthatr=ryr.Thusry∈Id(R).SinceRhasnonontrivialidempotents,sory=0orry=1.Nowifry=0,thenr=ryr=0whichisacontradiction.Thereforery=1andsinceRisdirectlyfinitesoyr=ry=1.Thusr∈U(R).SoRisweaklycleanring.

□

AringRisindecomposableprovidedId(R)={0,1},wecanhavethefollowingresult.

Corollary1LetRbeanindecomposablecommutativeweaklyr-cleanring,thenRisweaklyclean.

ProofThisisobviousbyTheorem1.

□

Now,wegivesomepropertiesofweaklyr-cleanrings.

Theorem2LetRbearing,thenx∈Risweaklyr-cleanifandonlyif1-xor1+xisr-clean.

ProofLetx∈Rbeweaklyr-clean.Thenx=r+eorx=r-e,wherer∈Reg(R)ande∈Id(R).Ifx=r+e,then1-x=-r+(1-e).Thereexistsy∈Rsuchthatr=ryr.Hence(-r)(-y)(-r)=-(ryr)=-randsince-r∈Reg(R)and1-e∈Id(R),so1-xisr-clean.Ifx=r-e,then1+x=r+(1-e)wherer∈Reg(R)and1-e∈Id(R),so1+xisr-clean.

Conversely,if1-xisr-clean,write1-x=r+ewherer∈Reg(R)ande∈Id(R).Thusx=-r+(1-e)where-r∈Reg(R)and1-e∈Id(R).If1+xisr-clean,write1+x=r+ewherer∈Reg(R)ande∈Id(R).Thusx=r-(1-e)wherer∈Reg(R)and1-e∈Id(R).SoRisaweaklyr-cleanring.

□

Theorem3Everyhomomorphicimageofweaklyr-cleanringsisweaklyr-clean.

ProofSee[3,Theorem8].

□

Remark1Ingeneral,theconverseofTheorem3maybenotcorrect.Forexample,ifpisaprimenumber,thenthehomomorphicimageZpZ≅Zpisweaklyr-clean,butZisnotweaklyr-clean.

Theorem4LetRbeanindecomposablering.Thenthefollowingconditionsareequivalent.

(1)Risaweaklyr-cleanring.

(2)x, x+1orx-1isregular.

Proof(1)⟹(2)SinceRisanindecomposableweaklyr-cleanring,soife=0, x=r;ife=1, x=r+1orx=r-1wherer∈Reg(R),thusx, x+1orx-1isregular.

(2)⟹(1)Letx∈R.Ifxisnotregularthenthereexistsx+1orx-1isregular.Thereforex=r+1orx=r-1wherer∈Reg(R).Ifxisregular,thenx=x+0.ThusRisaweaklyr-cleanring.

□

Lemma2AringRisar-cleanringifandonlyifeveryelementx∈Rcanbewrittenasx=r-ewherer∈Reg(R)ande∈Id(R).

Proof⟹LetRbear-cleanring,forx∈R, -x=r+ewherer∈Reg(R)ande∈Id(R).Thenx=(-r)-ewhere-r∈Reg(R)ande∈Id(R).

⟸Byhypothesis,everyelement-x∈Rcanbewrittenas-x=r-ewherer∈Reg(R)ande∈Id(R),thenx=-r+ewhere-r∈Reg(R)ande∈Id(R).SoRisar-cleanring.

□

Theorem5Let{Ri}beanonemptycollectionofringsRi.ThentheproductR=∏i∈IRiisweaklyr-cleanifandonlyifthereexistsm∈IsuchthatRmisweaklyr-cleanandRnisr-cleanforalln≠m.

Proof⟸SupposeRmisweaklyr-cleanandRnisr-cleanforalln≠m.Letx=(xi)∈R=∏i∈IRi.InRm,wecanwritexm=rm+emorxm=rm-emwhererm∈Reg(Rm)andem∈Id(Rm).

CaseI. xm=rm+em.Forn≠m,letxn=rn+enwherern∈Reg(Rn)anden∈Id(Rn).

CaseII. xm=rm-em.Forn≠m,letxn=rn-enwherern∈Reg(Rn)anden∈Id(Rn)byLemma2.

Thenr=(ri)∈Reg(Ri), e=(ei)∈Id(Ri),andx=r+eorx=r-e.

⟹SupposethatRisweaklyr-clean.Thenforeach(x,0,…)∈R,

(x,0,…)=(r,r1,r2,…)+(e,e1,e2,…)or(x,0,…)=(r,r1,r2,…)-(e,e1,e2,…)

where(r,r1,r2,…)∈Reg(R)and(e,e1,e2,…)∈Id(R),sor∈Reg(R1)ande∈Id(R1).SoR1isweaklyr-clean.Similarly,eachRiisweaklyr-clean.AssumethatthereexiststwoindicesmandnsuchthatneitherRmnorRnarer-clean.Thenthereexistsxm∈Rmandxn∈Rnsuchthatxmisnotasumofaregularandanidempotentandxnisnotadifferenceofaregularandanidempotent.Thus(xm,xn)isnotweaklyr-cleaninRm×Rn,whichisacontradiction.

□

Lemma3LetRbeacommutativering.ThenId(R)=Id(R[X] )=Id(R[[x]] ).

ProofSee[4,Lemma3.1].

□

Lemma4LetRbeacommutativering.

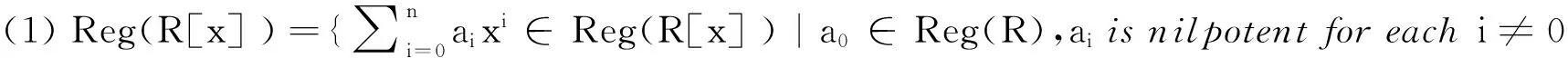
(2)Reg(R[[x]] )={∑aixi∈Reg(R[[x]] )|a0=ue,ai∈eRfor eachi≠0 for someu∈U(R) ande∈Id(R)}.

ProofSee[4,Theorem3.2].

□

Theorem6LetRbeacommutativering,thenR[x]isnotweaklyr-clean.

ProofWeshowthatxisnotweaklyr-clean.Supposethatx=r+eorx=r-ewherer∈Reg(R[x] )ande∈IdR[x] .ThenbyLemma3, Id(R)=Id(R[x] ),sox-eorx+eisregular.HencebyLemma4, 1shouldbenilpotent,whichisacontradiction.

□

LetRbeacommutativering.By[1] , RisweaklycleanifandonlyifR[[x]]isweaklyclean.LetRbeacommutativeweaklycleanring,thenRisweaklyr-clean.ItisobviousthatR[[x]]isweaklyr-clean.Butforeachweaklyr-cleanringR, R[[x]]maybenotweaklyr-clean.

□

Corollary2LetR=Z[x] ,thenR[[x]]isnotweaklyr-clean.

ProofLetR=Z[x] ,thenRisnotr-cleanbyTheorem6.SinceR[[x]]/(x)=R,sobyTheorem3, R[[x]]isnotweaklyr-clean.

□

Theorem7LetRbearingandeisacentralidempotentelementofR.ThenRisweaklyr-cleanringifandonlyifoneofeReand(1-e)R(1-e)isweaklyr-clean,andtheotheroneisr-clean.

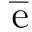
ButidempotenteinRarecentral,so

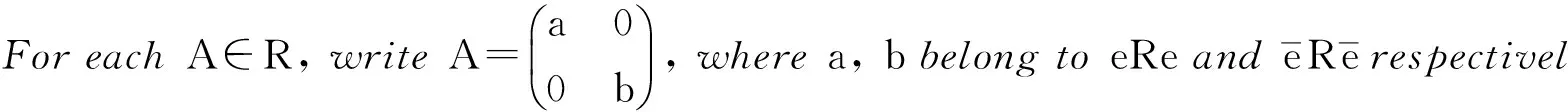
CaseI,ifa=r1+e1,letb=r2+e2,wherer1, r2∈Reg(R)ande1, e2∈Id(R).So

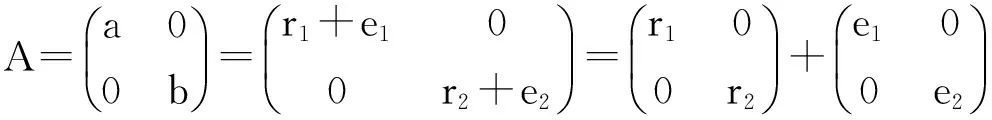
Thereexistsy1,y2∈Rsuchthatr1y1r1=r1, r2y2r2=r2.Therefore

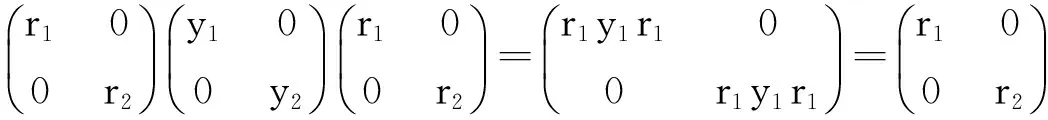
CaseII,ifa=r1-e1,letb=r2-e2,wherer1, r2∈Reg(R)ande1, e2∈Id(R).So

⟹SinceidempotenteinRiscentral,so

ByTheorem5,supposeRisaweaklyr-cleanring,thenoneofeReand(1-e)R(1-e)isweaklyr-clean,andtheotheroneisr-clean.

□

Corollary3LetRbearingande1,…,enbeorthogonalcentralidempotentswithe1+…+en=1.ThenRweaklyr-cleanifandonlyifthereexistsisuchthateiReiisweaklyr-cleanandejRejisr-cleanforalli≠j.

ProofLetRbeaweaklyr-cleanringande1,…,enbeorthogonalcentralidempotentswithe1+…+en=1.ThenR=e1Re1⊕…⊕enRen,thenbyTheorem5,thereexistsisuchthateiReiisweaklyr-cleanandejRejisr-cleanforalli≠j.

Conversely,ifthereexistsisuchthateiReiisweaklyr-cleanandejRejisr-cleanforalli≠j,itisobviousthatRbeaweaklyr-cleanringbyinductionofTheorem7.

□

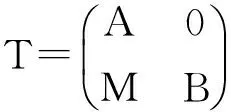
or

a=r1+f1,b=r2+f2ora=r1-f1,b=r2-f2.

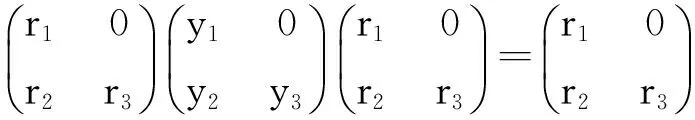
So

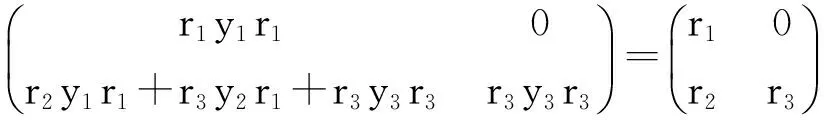
Hencer1∈Reg(A)andr3∈Reg(B).Itiseasytocheckthatf1∈Id(A)andf3∈Id(B).Thereforeaandbareweaklyr-clean.HenceAandBareweaklyr-clean.

□

LetRbeacommutativeringandMbeanR-module.Thesetofpairs(r,m)withr∈Randm∈M,undertheadditiondefinedby(r,m)+(r′,m′)=(r+r′,m+m′)andthemultiplicationdefinedby(r,m)(r′,m′)=(rr′,rm′+r′m),forallr,r′∈R, m,m′∈M.ThenR(M)iscalledthetrivialextensionofRandM.

Corollary4LetRbearingandletMbeanR-module.ThetrivialextensionR(M)ofRandMisaweaklyr-cleanring,thenRisweaklyr-clean.

ProofItisobviousbyTheorem8.

□

Lemma5LetRbeacommutativeringG={1,g}beagroup.Thenr+sg∈Reg(RG)ifandonlyifr+s∈Reg(RG).

ProofSee[6,Lemma2.1] .

□

Lemma6LetRbeacommutativeringandG={1,g}beagroup.Thenr+sg∈Id(RG)ifandonlyifr+s∈Id(RG)andr-s∈Id(RG).

ProofSee[6,Lemma2.2] .

□

Theorem9LetRbeacommutativeringandG={1,g}beagroup.Thenthefollowingconditionsareequivalent.

(1)Risaweaklyr-cleanring.

(2)Foreacha∈R, ag∈RGisweaklyr-clean.

Proof(1)⟹(2)Leta∈R,thena=r+eora=r-ewherer∈Reg(R)ande∈Id(R).Soag=rg+egorag=rg-eg.ByLemma5andLemma6, rg∈Reg(RG)andeg∈Id(RG).Henceag∈RGisweaklyr-clean.

(2)⟹(1)Let

φ:RG→R,

It is obvious thatφis a map. For eacha∈R, supposeag∈RGis weaklyr-clean, then

ag=(r1+r2g)+(e1+e2g)

or

ag=(r1+r2g)-(e1+e2g),

wherer1+r2g∈Reg(RG) ande1+e2g∈Id(RG). Then

a=φ(ag)=(r1+r2)+(e1+e2)

or

a=φ(ag)=(r1+r2)-(e1+e2).

By Lemma 5 and Lemma 6,r1+r2∈Reg(R) ande1+e2∈Id(R), soais weaklyr-clean. HenceRis a weaklyr-clean ring.

□

Likewise, we have the following condition.

Corollary 5LetRbe a commutative ring andG={1,g} be a group. ThenRis a weaklyr-clean ring if and only if for eacha∈R,a∈RGis weaklyr-clean.

Theorem 10LetRbe a ring， letSbe an indecomposable homomorphic image ofRand letGbe locally finite group. ThenRGis a weaklyr-clean ring if and only ifSGis weaklyr-clean.

Proof⟹ SinceSis a homomorphic image ofR, ThenSGis a homomorphic image ofRG. By Theorem 3,SGis weaklyr-clean.

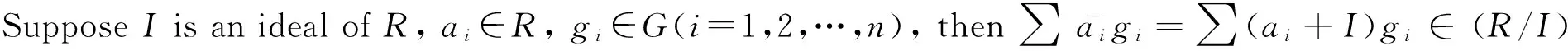
SupposeRGis not weaklyr-clean ring, then there exists finite subsetKofGsatisfying that ∑gi∈Kaigi∈RG is not weaklyr-clean whereai∈R. Let

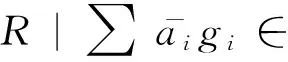
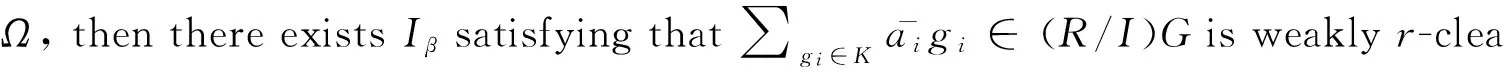
SinceGis locally finite group, then there exists finite subgroupHsatisfying thatK⊆H. So

or

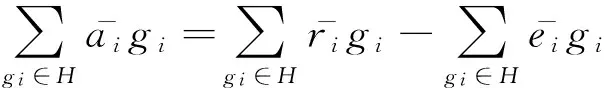
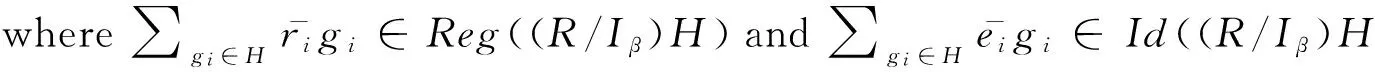
By Zorn’s Lemma,Ωcontain a maximal elementA. The maximality ofR/A∈Ωimplies thatR/Ais indecomposable as a ring. LetR/A=S1/A⊕S2/AwhereA⊂S1andA⊂S2. Then

S1/A≅R/A/S2/A=R/S2

and

S2/A≅R/A/S1/A=R/S1,

So

(R/A)G≅(R/S1)G⊕(R/S2)G.

The maximality ofR/A∈Ωimplies that ∑gi∈K(ai+S1)gi∈(R/S1)G and ∑gi∈K(ai+S2)gi∈(R/S2)G is weaklyr-clean. Then

□

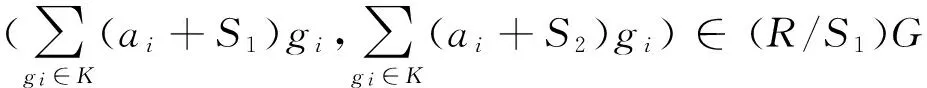
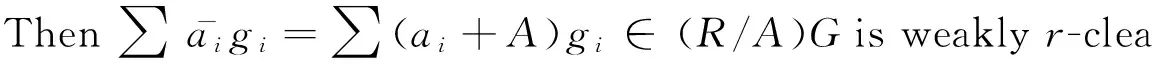
References:

[1] AHN M S. Weakly clean rings and almost clean rings[D]. Iowa City: The University of Iowa,2003.

[2] HANDELMAN D. Perspectivity and cancellation in regular rings [J]. J Algebra,1977,48(1):1-16.

[3] ASHRAFI N, NASIBI E.R-clean rings[J]. Mathematical Reports,2011,15(2):125-132.

[4] DAVID F A, BADAWI A. Von Neumann regular and related elements in commutative rings [J]. Algebra Colloq,2012,19(19):1017-1040.

[5] ANDERSON D D, CAMILLO V P. Commutative rings whose elements are a sum of a unit and idempotent [J]. Comm Algebra,2002,30(7):3327-3336.

[6] WANG S H.R-clean group rings and stronglyr-clean rings[D]. Guilin: Guangxi Normal University,2013.

Received date：2015-06-16

Foundation item：Supported by the Natural Science Foundation of Zhejiang Province (LY13A010019).

Corresponding author：CHEN Huanyin (1963—), male, Professor, Ph.D., majored in non-commutative algebra and K-theory. E-mail：huanyinchen@aliyun.com

doi:10.3969/j.issn.1674-232X.2016.04.011

CLC number:O153.3MSC2010: 16E50; 16S34; 16U10Article character: A

关于Weaklyr-clean环

孟文静， 陈焕艮

(杭州师范大学理学院，浙江 杭州310036)

摘要:定义了weakly r-clean环. 环R叫做weakly r-clean环, 如果对于任意一个元素x∈R 可以写成x=r+e或x=r-e的形式, 其中r∈Reg(R)且e∈Id(R). 首先, 证明了在什么情况下weakly r-clean环是weakly clean的. 然后, 得到了weakly r-clean环的一些性质. 进而推广了r-clean环的相应结果.

关键词:clean环; 正则元; 幂等元; r-clean 环; weakly r-clean环