Itô积分和Str atonovich积分的比较

王 伟

（浙江科技学院 理学院，杭州310023）

1 Introduction

In this paper，we consider the t wo kinds of stochastic integrals，the Itôintegral and the Stratonovich integral.Let（Ω，F）be a measure space with t he pr obability measure P and Bt（ω）be a n-dimensional Bro wnian motion.Assu me t hat Ft＝F（n）tis theσ-algebra generated by t he rando m variables｛Bi（s）｝1≤i≤n，0≤s≤t.We denote by V（S，T）the class of f unctions.

such that

1）（t，ω）→f（t，ω）is B×F-measurable，where B denotes t he Borelσ-al gebra on［0，∞）；

2）f（t，ω）is Ft-adapted；

We adopt L2（P）to be a Hil bert space which is a co mplete inner pr oduct space wit h t he f ollo wing inner product.

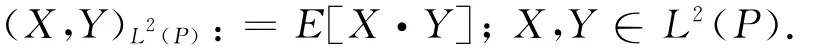
Definition 1 （Itôintegral） Suppose f∈V（0，T）and that t→f（t，ω）is continuous f or a.a.ω.Then t he Itôintegral is defined by

Definition 2 （Str atonovich integral） Suppose f∈V（0，T）and t hat t→f（t，ω）is continuous f or a.a.ω.Then t he Str atonovich integral of f is defined by

whenever t he limit exists in L2（P）.

2 Itôfor mula

Theorem 1 （Itôf or mula） Let Xtbe an Itôprocess given by

Asssu me g（t，x）∈C2（［0，∞）×R）（i.e.g is t wice continuously diff erentiable on［0，∞）×R）.Then

is also an Itôprocess，and we have

where（d Xt）2＝（d Xt）·（d Xt）is computed according to the r ules

By the Itôfor mula（1），we get

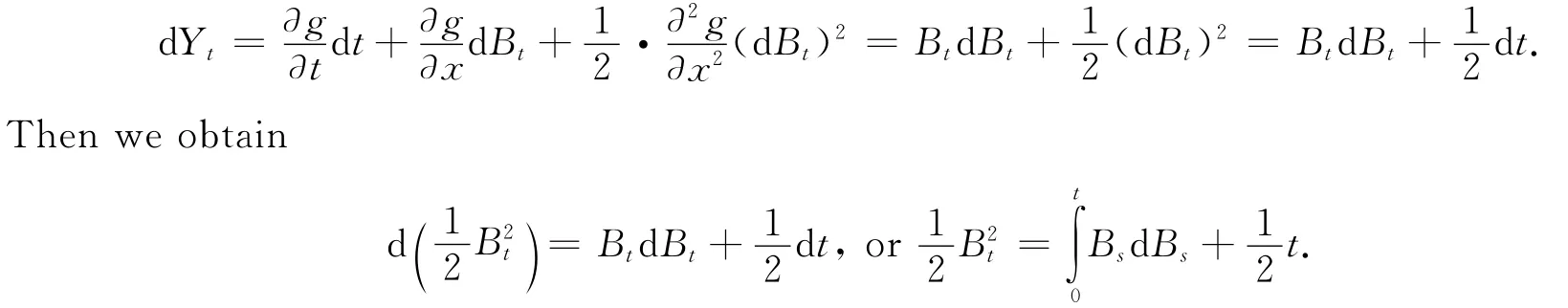
So，we get the value of this Itôintegral as the f ollowing

3 Relationship bet ween the Itôintegral and the Stratonovich integral

Theorem 2 Suppose f∈V（0，T）and that t→f（t，ω）is continuous f or a.a.ω.Then

Proof Suppose f∈V（0，T）and that t→f（t，ω）is continuous for a.a.ω.Then，

Now we can use t he Theorem 2 to co mpute so me Str atonovich integrals.

We see the different values of the t wo kinds of integrals clearly through the Example 1 and the Example 2.

4 Application in the stochastic differential equations

Example 3 Solve the following stochastic equation，which is a well-known population growth model

Sol ution The equation（3）can be written as

By the Itôfor mula，we have

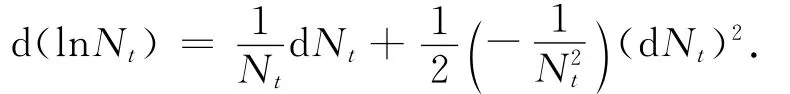
By t he equation（3），we obtain（d Nt）2＝ （r Ntd t＋αNtd Bt）2＝α2N2t（d Bt）2＝α2N2td t.So we get

Then we can concl ude

Exa mple 4 The Str atonovich inter pretation of stochastic equation（3）is

Solve this stochastic equation.

Solution By the Theorem 2，we have

We call such a process Geometric Brownian motion.It is also an important model for stochastic prices in econo mics［1］.

5 Contrast bet ween the Itôintegral and the Str atonovich integral

At t he end，let us ret ur n to t he population gro wt h model in t he Exa mple 3.We know that Ntis a solution of the stochastic equation（3），and

For some suitable interpretation of the last integral in the equation（5），the Itôinterpretation of an integral is j ust one of t he several reasonable choices.However，t he Str atonovich integral is anot her choice，usually leading to a diff erent result.So t he question is：Which inter pretation of t he last integral in the equation （5）makes the equation the “exact”mathematical model for this equation？The Str atonovich interpretation in so me situations may be the most appropriate.Choose t-continuously differentiable pr ocesses B（n）tsuch that f or a.a.ω，

unif or mly（in t）in bounded inter vals.For eachωlet N（n）t（ω）be t he sol ution of the corresponding（deter ministic）differential equation

Then，f or a.a.ω，

unif or mly（in t）in bounded intervals.

It t ur ns out［2-3］t hat t his sol ution Ntcoincides wit h t he sol ution of t he equation （5）obtained by using t he Str atonovich integral

This outco me implies that Ntis the sol ution of the following modified the Itôequation，

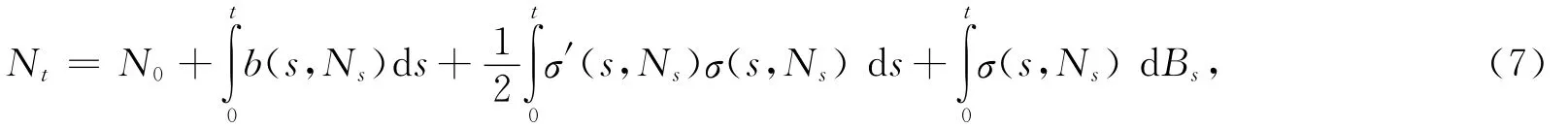
whereσ′denotes the derivative ofσ（t，x）w.r.t.x［4］.

Theref ore，fro m t his point of view it seems reasonable to use t he Str atonovich inter pretation of t he equation（6），and not t he Itôinter pretation of t he equation（5）as t he model f or t he original white noise equation.However，t he specific f eat ure of t he Itômodel of“not l ooking into t he f ut ure”［5］seems to be a reason f or choosing the Itôinterpretation in many cases，for example in biology［6］.Note that equation（5）and（7）coincide ifσ（t，x）does not depend on x［7］.

By t he Theorem 2，we can find t hat t here is no second or der ter m in t he Str atonovich analogue of the Itôtransf or mation for mula.It can be said that the Str atonovich integral has the advantage of leading to or dinary chain r ule for mulas under a transf or mation.This advantage makes the Str atonovich integral good to use f or exa mple in connection wit h stochastic diff erential equations on manif ol ds［8-9］.However，the Stratonovich integrals are not martingales，but the Itôintegrals are.This gives the Itôintegral an important computational advantage，even though it does not behave so nicely under transfor mations.

［1］ Kallianpur G，Karandikar R L.Introduction to Option Pricing Theor y［M］.Boston：Bir khäuser，2000.

［2］ Wong E，Zakaim.Riemann-Stieltjes approximations of stochastic integrals［J］.Probability Theory and Related Fields，1969，12（2）：87-97.

［3］ Sussmann H J.On the gap bet ween deter ministic and stochastic ordinary differential equations［J］.The Annals of Probability，1978，6（1）：19-41.

［4］ Stratonovich R L.A new representation for stochastic integrals and equations［J］.SIA M Jour nal on Control，1966，4（2）：362-371.

［5］ Ber ntØksendal.Stochastic Differential Equations［M］.6 ed.Beijing：World Publishing Cor poration，2006.

［6］ Turellim.Random environments and stochastic calculus［J］.Theoretical Population Biology，1977，12（2）：140-178.

［7］ Benth F E.Option Theory with Stochastic Analysis［M］.Heidelberg：Springer-Verlag，2004.

［8］ El worthy K D.Stochastic Differential Equations on Manif olds［M］.Cambridge：Cambridge University Press，1982.

［9］ Ikeda N，Watanabe S.Stochastic Differential Equations and Diff usion Processes［M］.2 ed.Amster dam：North-Holland／Kodansha，1989.