极坐标系下可处理多普勒量测的BLUE跟踪算法

李　丹,王　炜

(1.武汉理工大学理学院,湖北武汉430070;2.海军工程大学理学院,湖北武汉 430033)

极坐标系下可处理多普勒量测的BLUE跟踪算法

李丹1,王炜2

(1.武汉理工大学理学院,湖北武汉430070;2.海军工程大学理学院,湖北武汉 430033)

事实已表明包含目标速度信息的多普勒量测具有有效提高目标状态估计精度的潜力.该文在直角坐标系下提出两种可使用转换多普勒量测(即距离量测与多普勒量测的乘积)的滤波器,一种借助了构造的多普勒伪状态,另一种没有借助多普勒伪状态.从理论上讲,它们都是在最佳线性无偏估计准则下的最优线性无偏滤波器,并且避免了量测转换方法的根本缺陷.通过将近似处理后的两种新型最优线性滤波器与目前几种流行的方法进行仿真比较,验证了所提出的滤波器的优越性.

目标跟踪;多普勒;最佳线性无偏估计;量测转换

1　引言

基于目标位置量测的量测转换方法已被广泛使用在目标跟踪中,使得卡尔曼滤波器得以在直角坐标系中应用,但是量测转换方法有一些会导致估计性能恶化的根本缺陷.事实上,除位置量测外,无论量测源确定与否,充分利用多普勒量测是可以有效提高目标状态估计精度的[1,2].研究表明:斜距和多普勒量测的量测误差对于某些雷达波形而言常常是统计相关的[1].为减小直角坐标系下的多普勒量测模型的强非线性,学者们通过将斜距和多普勒量测相乘构造了伪量测.基于此,为充分利用雷达多普勒量测信息,文献[3]将 (Debiased Converted Measurement,DCM) 卡尔曼滤波算法推广为包含多普勒量测且斜距误差和多普勒误差相关的序贯滤波算法.文献[4]基于修正的无偏量测转换(Modified Unbiased Converted Measurement,MUCM) 提出序贯量测转换卡尔曼滤波方法.文献[5]没使用伪量测,而是直接基于多普勒量测,使用无迹变换(Unscented Transform,UT)进行序贯卡尔曼滤波.文献[6]则是基于视线坐标转换和信息滤波思想提出的.文献[7]首先使用极坐标位置量测,并经过量测转换卡尔曼滤波估计出目标位置状态,然后通过使用转换多普勒量测,并经过卡尔曼滤波估计出转换多普勒伪状态,最后使用最小方差估计准则组合多普勒伪状态估计和目标位置状态估计,并得出最终估计结果.该算法的性能优于文献[3,5,8,9]提出的算法.

基于BLUE准则,本文导出两种直接使用极坐标系中的雷达位置量测和多普勒量测的近似BLUE滤波算法,可以直接使用极坐标下的雷达量测对目标的直角坐标运动状态进行估计,在估计误差和滤波器可靠性方面都明显超过量测转换方法.同时,文中也将文献[5]的算法扩充到极坐标系下.最后,将这两种新算法与现有的5种多普勒量测处理算法[3～7]作出仿真比较.

2　量测方程

首先,将极坐标位置量测转换到直角坐标系后产生

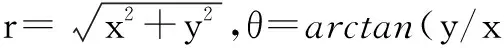
然后,为减弱多普勒量测和目标运动之间的强非线性程度,构造伪量测方程

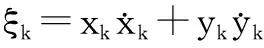
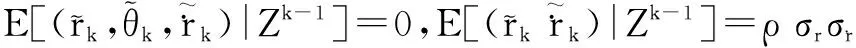
本文规定:若在某变量头顶上加“-”,则表示该变量的时间更新估计;若加“^”,则表示该变量的量测更新估计.

3　不使用多普勒伪状态的BLUE跟踪算法

考虑如下随机系统

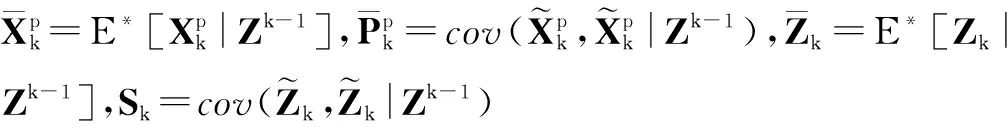
具体的计算公式如下[10]:

另外,Sk(i,j)(i,j=1,2)的公式可参见文献[11].

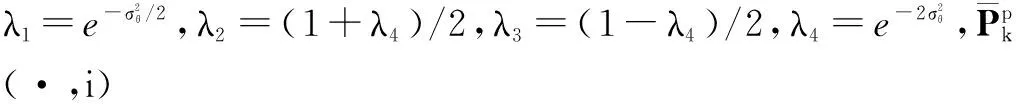
4　使用多普勒伪状态的BLUE跟踪算法

本节的目的是将文献[7]所提出的算法(简记为SFCMKP)作出改进.改进的算法简记为BLUESF.由于SFCMKP算法在估计目标位置状态时,使用了加性去偏卡尔曼滤波算法[8],从而引入了量测转换方法的本质性缺陷,理论上导致该算法性能打折扣.BLUESF算法通过使用文献[11]提出的BLUE位置滤波算法代替加性去偏卡尔曼滤波算法,克服了量测转换方法的缺陷.

首先,BLUESF算法使用极坐标位置量测,由BLUE位置滤波算法估计出目标位置,然后通过使用多普勒伪量测和多普勒伪状态方程,经由卡尔曼滤波器估计出多普勒伪状态,最后使用BLUE准则融合目标位置状态和多普勒伪状态,得出最终的估计结果.考虑到两算法的主要异同点,为节省篇幅,本节主要给出BLUESF算法中目标位置状态和多普勒伪状态的互相关的推导过程,并没有给出完整的BLUESF算法.又由于SFCMKP算法和BLUESF算法的推导过程必须使用近常速(Nearly Constant Velocity,NCV)模型,所以这里也描述了NCV模型.

4.1目标运动方程

NCV模型使用零均值白噪声来建模对速度的轻微扰动,NCV模型的具体表达如下

也即,

4.2目标位置状态和多普勒伪状态的互相关

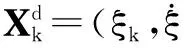
其中,

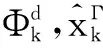
5　极坐标系下的DCML算法

本文的仿真部分需要将2种新算法与5种经典的可处理多普勒量测的滤波方法在极坐标系下进行比较,而文献[5]中的DCML算法仅是在球坐标系下导出的,所以需要导出极坐标系下的DCML算法.事实上,若要导出极坐标系下的DCML算法,只需将球坐标系下DCML算法的转换量测方程、转换量测误差均值和协方差替换为极坐标情形即可.

相应的转换量测误差的协方差为

其中,

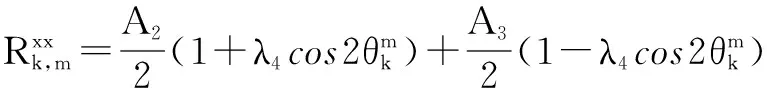
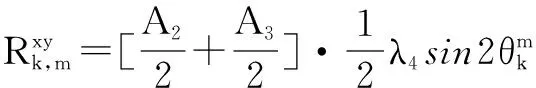
其中,

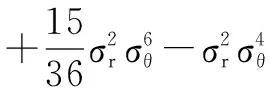
6　仿真结果

我们选择了5种IEEE库中理论依据合理的可处理多普勒量测的跟踪算法(分别记为DCMD[3],UCMD[4],DCML[5],CMKFRR[6]和SFCMKP[7]),与BLUEPM算法和BLUESF算法进行仿真比较.所有算法使用了相同的目标初始状态估计及其估计误差协方差矩阵.另外,为便于观察算法的最优性能,我们在仿真结果中加入了由真实目标状态值计算出的位置和速度罗-克拉美下界(Posterior Cramer-Rao Low Bound,PCRLB)曲线.

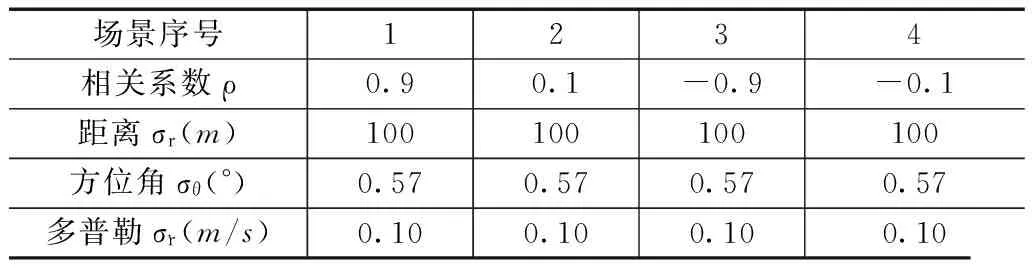
表1　仿真中4种不同场景的参数设置表

这几种场景可以对比反映出参数设置值的变化,以便对算法跟踪误差随参数设置值改变而作出的改变做比较.比如,场景1和场景2对应的相关系数ρ由0.90变至0.10,而其他参数不变的情形.此时,在相关系数小的场景2下,DCML算法、CMKFRR算法、SFCMKP算法、BLUEPM算法和BLUESF算法几乎显示了差别不大的跟踪性能,而在相关系数大的场景3下,DCML算法的跟踪性能要劣于CMKFRR算法、SFCMKP算法、BLUEPM算法和BLUESF算法.这表明:在相关系数很小的场景下多普勒量测可能并不能对BLUEPM算法和BLUESF算法的跟踪性能有多大改进.

从所有仿真结果图可看出:DCMD算法和UCMD算法跟踪性能最差,它们的位置估计RMSE呈直线增长趋势,而速度估计RMSE呈固定常值状态,位置和速度RMSE曲线远离相应场景下的位置和速度PCRLB曲线;SFCMKP算法,BLUEPM算法和BLUESF算法的位置和速度RMSE曲线离相应场景下的位置和速度PCRLB下界曲线最近;SFCMKP算法和BLUESF算法在某些场景下滤波一开始出现了较大峰值,随后便消失,而BLUEPM算法在所有场景下整条RMSE曲线较平缓且无大峰值;DCML算法的位置估计RMSE曲线介于DCMD算法和BLUEPM算法的位置估计RMSE曲线的中间位置处,而DCML算法的速度估计RMSE曲线与BLUEPM算法的速度估计RMSE曲线几乎总交织在一起且差别并不大;CMKFRR算法的位置估计RMSE曲线在一部分场景下几乎与SFCMKP算法的相重合,而在另一部分场景下CMKFRR算法却会出现几个大峰值,但该算法的速度估计RMSE曲线几乎在所有场景下总出现大峰值.

图9给出的7种算法的平均单次执行时间,可看出,BLUEPM算法的执行时间最短,为SFCMKP算法的近1/20.CMKFRR算法次之,为BLUEPM算法的近两倍.BLUESF算法,DCML算法和SFCMKP算法的执行时间几乎相同.UCMD算法和DCMD算法的几乎相同,约为SFCMKP算法的1/2.

总而言之,从综合性能讲,BLUEPM算法是执行时间最短,跟踪精度最好的算法.BLUESF算法和SFCMKP算法次之,它们除在某些初始跟踪时刻估计误差偶尔增大外,整体跟踪性能良好,但执行时间长些.紧接着,便是DCML算法.而CMKFRR算法随着仿真场景的变化会时好时坏.UCMD算法和DCMD算法的跟踪性能最差.

7　结论

本文讨论了同时使用位置量测和多普勒量测进行目标跟踪的问题,其中距离量测与多普勒量测之间可以是相关的.在该问题框架下提出两种可使用转换多普勒量测的滤波算法.从理论上讲,它们是在BLUE准则下的最优线性滤波器,避免了量测转换方法的根本缺陷.通过仿真实验,将所提出的两种新算法与5种流行方法的跟踪性能进行了比较和验证.依照RMSE和CRLB度量准则,新算法明显优于其他几种流行方法.

[1]Bar-Shalom Y.Negative correlation and optimal tracking with Doppler measurements[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37 (3):1117-1120.

[2]Musicki D,Song T L,Lee H H.Correlated Doppler-assisted target tracking in clutter[J].IET Radar,Sonar & Navigation,2013,7 (1):94-100.

[3]Duan Zhansheng,Li Xiaorong,Han Chongzhao,et al.Sequential nonlinear tracking filter with range-rate measurements in spherical coordinates[A].Proceedings of 7th International Conference on Information Fusion[C].Stockholm:International Society of Information Fusion,2004.131-138.

[4]Jiao LianMeng,Pan Quan,Yan Liang,et al.A nonlinear tracking algorithm with range-rate measurements based an unbiased measurement conversion[A].Proceedings of 15th International Conference on Information Fusion[C].Singapore,2012.1400-1405.

[5]Lei Ming,Han Chongzhao.Sequential nonlinear tracking using UKF and raw range-rate measurements[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43 (1):239-250.

[6]Bordonaro S V,Willett P,Bar-Shalom Y.Performance analysis of the converted range rate and position linear Kalman filter[A].Proceedings of 47th Asilomar Conference on Systems and Computers,Signals[C].California:IEEE Computer Society,2013.1751-1755.

[7]Zhou Gongjian,Pelletier Michel,Kirubarajan Thiagalingan,et al.Statically fused converted position and Doppler measurement Kalman filters[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50 (1):300-316.

[8]Lerro D,Bar-Shalom Y.Tracking with debiased consistent converted measurements vs EKF[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29 (3):1015-1022.

[9]Duan Zhansheng,Han Chongzhao,Li Xiao-rong.Comments on “unbiased converted measurements for tracking”[J].IEEE Transactions on Aerospace and Electronic Systems,2004,40 (4):1374-1377.

[10]Wang Wei,Li Dan,et al.The best linear unbiased estimation algorithm with the Doppler measurements [J].Journal of Electronics & Information Technology,2015,37(6):1336-1342.(in Chinese)

[11]Zhao Zhan-lu,Li Xiao-rong,Jilkov V P.Best linear unbiased filtering with nonlinear measurements for target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,2004,40 (4):1324-1336.

李丹女，1980年5月出生,湖北随州人.2015年在武汉理工大学获博士学位.武汉理工大学理学院教师,主要从事统计学、信息处理方面的研究.

E-mail:lidan0520@163.com

王炜(通信作者)男，1975年8月出生,山西长治人.2011年在华中科技大学获博士学位.现为海军工程大学理学院教师,主要从事信息与信号处理、信息融合方面的研究.

The BLUE Tracking Algorithm with the Doppler Measurementsin the Polar Coordinates

LI Dan1,WANG Wei2

(1.School of Science,Wuhan University of Science and Technology,Wuhan,Hubei 430070,China; 2.School of Science,Naval University of Engineering,Wuhan,Hubei 430033,China)

In fact,the Doppler measurement containing information of target velocity has the potential capability of improving the tracking performance.Two filters are proposed which can use converted Doppler measurements ( i.e.the product of the range measurements and Doppler measurements ) in the Cartesian coordinates.One filter uses the Doppler pseudo-states;another doesn’t use the Doppler pseudo-states.These novel filters are theoretically optimal in the rule of the best linear unbiased estimation in the Cartesian coordinates,and they are free from the fundamental limitations of the measurement-conversion approach.Based on simulation experiments,the approximate,recursive implementations of these two novel filters are compared with those obtained by five state-of-the-art conversion techniques recently.Simulation results demonstrate the effectiveness of the proposed two filters.

target tracking;Doppler;best linear unbiased estimation(BLUE);converted measurement

2014-12-29;

2015-10-10;责任编辑：李勇锋

国家自然科学基金(No.11571133，No.51307128);中央高校基本科研业务费专项资金(No.2015IA005);海军工程大学自然科学基金(No.HJGSK2014G121)

TP391

A

0372-2112 (2016)07-1656-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.07.020