相干位移操作辅助下的量子放大器研究
2016-08-09郭建胜张胜利
王 琨,郭建胜,2,张胜利
(1.解放军信息工程大学,河南郑州 450004;2.信息保障技术重点实验室,北京 100000)
相干位移操作辅助下的量子放大器研究
王琨1,郭建胜1,2,张胜利1
(1.解放军信息工程大学,河南郑州 450004;2.信息保障技术重点实验室,北京 100000)
本文针对位移操作辅助下的量子线性放大器进行了研究.量子线性放大器可以提高量子态传输的保真度,提高量子通信抗干扰、抗损耗能力.本文针对目前量子线性放大器放大增益和放大成功概率低的问题,提出了相干位移增强型量子线性放大器,给出了位移操作提升量子线性放大器的机制,推导出放大增益得以进一步提高所需的位移操作的阈值,并结合态空间向光子数空间转化定理,在0-1光子数空间和多光子空间中同时验证了放大增益对位移量之间的依赖关系.
量子光场;量子位移操作;量子线性放大器
1 引言
随着量子理论研究的不断深入,基于量子技术的信息处理研究成为当前的一个研究热点[1~3].环境噪声的影响是制约量子技术应用的重要因素之一,而量子放大是一种概率性克服环境噪声的方法,它对损耗后的量子态进行概率性地放大,以几乎没有附加噪声的方式实现对较弱的量子信号进行放大.而且这种放大是可标记性的放大,通过对标记探测器的观察,可以准确地知道每一次放大是否成功.2009年,T C Ralph和A P Lund基于光学提出了对光子量子比特的放大方案[4](以下简称Ralph方案).该方案结构简单巧妙,只需要两个单光子探测器以及一个辅助的单光子态,即可以实现对于弱相干态的放大.其放大器的放大增益可以通过分束器的透过系数加以灵活调节.而且,Ralph等人还证明了该放大器可以应用到连续变量两模纠缠态的分发过程中.在一般的纠缠分发过程中,发送方将纠缠着的两个模式的其中一个通过有损耗的信道发送给接收方.这个有损信道又称为振幅衰减信道(Amplitude Damping Channel),其中的振幅衰减噪声可以通过量子放大器概率性地得到消除,从而在发送方和接收方之间形成没有噪声的纯态纠缠.
量子放大方案的提出得到了国内外学者的广泛重视.在Ralph方案的基础上,大量的后续研究工作得以开展.大体上,这些研究主要分为以下两类:
(1)优化量子放大方案,提高放大方案的放大增益和成功概率.如:J Jeffers拓展了量子放大方案的研究对象,将以单光子放大为主的量子放大方案拓展到了双光子成分的放大[5].J Fiuráek等人利用光子湮灭算符和光子产生算符的组合,提高了量子放大方案的放大增益和成功概率[6].Zhang Shengli等人考察了基于开关型光子探测器和标记单光子态的更加实际的放大器,通过建立量子放大的相空间理论[7],研究了当薛定谔猫态作为输入时的量子放大方案[8].同时,也分析了当输入纠缠为单光子路径纠缠时,Ralph方案的放大增益以及相关的成功概率.
(2)研究量子放大方案在量子信息处理中的应用.Jonatan Brask等人利用放大器降低了无陷门贝尔不等式,验证了实验对于光子探测器效率以及光路损耗的要求[9].Rémi Blandino等人在连续变量量子密码GG02协议[10]中应用了Ralph方案,他们从理论上证明了Ralph方案可以将现有的GG02协议对光子损耗的承受能力提高12dB[11].在1550nm的通讯波段,这相当于将实际的密钥分配距离延长了48公里.J Fiuráek和Nicolas J Cerf证明了量子放大对于连续变量量子密码的增强作用,将其等效为一种对测量结果的高斯型后选择[12].通过这种后选择,等价地在量子密码通讯的光学线路上实现了一种虚拟的量子放大器,这为实现更加有效的连续变量量子密码方案提供了借鉴.
在实验研究方面,量子放大方案在光学系统中得到了大量的实验验证.国际上第一个量子放大的实验由项国勇和Ralph等人实现[13].他们完整实现了Ralph的方案,并验证了量子放大方案在弱相干态的放大和两模纠缠态的放大中的成功应用.随后,德国马普光科学研究所G Leuchs小组结合了非相干噪声和光子擦除技术实现了对位相相干信息的放大[14].最近,项国勇等又借助于光学参量下转换和两个放大过程实现了对单个偏振光子的放大[15].数据分析表明,这一放大可以把偏振光子在有损信道中的传输速率提高5倍,这对于实际可行的量子信息和量子精密测量具有实际意义.

2 相干位移操作辅助下的量子放大器方案

如图1所示,模式B的输出(output)是输出光学模式.一般来说,如果探测器D1探测到“0”光子,探测器D2探测到“1”光子,则模式B输出的就是把模式A的输入态成功放大后的量子态.设模式A的输入态是一个弱相干态,可以近似看成真空态和单光子态的叠加态,即|ψα〉=|0〉+α|1〉,其中α>0.
幺正算符UBC(t)描述的是分束器的演化,t代表分束器BS2的透过率,它作用在模式B和C的输入态|0〉B|1〉C上,得到
|ψBC〉=UBC(t)|0〉B|1〉C
(1)
单模位移算符D(β)作用在C模式上,得到

(2)
然后,模式C和模式A经过BS2这个50:50分束器耦合,耦合后的态经过两个单光子探测器探测,如果探测器的输出结果是:D1测到“0”光子,D2测到“1”光子,那么模式B输出的态就是成功放大的态.事实上,这个光子探测的过程可以等效成一个隐形传态和同时放大的过程.模式B输出态的数学表述形式如下

(3)

3 物理实现量子放大器方案中的位移算符
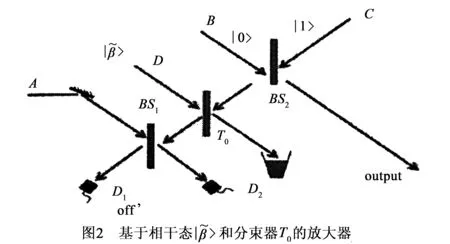
事实上,这种替代方式已经在实验上实现,并且是实验中一种比较成熟的技术.下面的分析中将原先的理想单光子探测器D1和D2替换成开关型光子探测器.
首先,模式B和模式C经过BS2分束器后,和模式D在透过率为T0的分束器耦合,此时输入的量子态可以表示为


(4)
经过透过率为T0的分束器耦合后,得到


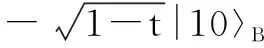
(5)

(6)
通过对模式D求迹,光学模式B和C成为一个混态,数学表达式如下:
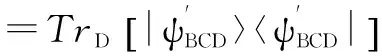

(7)






(8)
当T0→1时,
(9)
实现了单模位移算符D(β)的作用.


=c0(|0〉+Δ2αg|1〉)(〈0|+Δ2αg〈1|)
(10)
其中



图3(a)中,给出了位移算符的引入带给放大器的增益带来的变化.取输入相干态为一个弱相干态α=0.2.当-1<β<0时,Δ1>1,增益得到了进一步放大.图3(b)中,研究了T0=0.8和T0=0.9时的Δ2对于β的依赖关系.Δ=1是一个分界线,它意味着增益保持不变,只有Δ>1表示了增益得到了放大.
4 基于现实单光子源的放大方案
图1和图2中的单光子态是放大方案中尚没有解决的问题.然而,单光子本身的制备问题是一个无法解决的问题.现在最好的办法是基于光学参量下转化技术的标记单光子源[15~18].

λ=tanh(r)
(11)
如果单独考察光学模式C的量子态,它是一个混态
(12)
需要说明的是,模式C这里的两模压缩与基于局域压缩的放大中的压缩是不同的.这是因为模式C中压缩的功能是提供单光子,而压缩越弱越好.当压缩趋近于0时,ρC趋向于单光子|1〉〈1|.

(13)
其中,ρ(Vj,Rj)是协方差矩阵为Vj一阶量为Rj的高斯态.相关的计算技术已经十分成熟并被广泛应用于贝尔不等式的验证上,对于每一个高斯态ρ(Vj,Rj),可以很容易地推导出其密度矩阵,在图5和表1中给出了相应的计算结果.

(14)

基于上述分析,取与图5中相同的基本参数,即α=0.16,r=0.12,T0=0.8,t=0.1.利用MATLAB软件进行了数据模拟,根据数值模拟的结果,给出了基于位移算符和基于压缩算符的放大器成功概率对比情况,详见表1.

表1 达到固定增益geff时的ξ和

5 结束语
本文讨论了局域位移算符在放大器中的应用.进一步讨论了基于相干态以及光学分束器的位移算符的实现方法,在0-1子空间中验证了放大的增益.最后,解决了放大器对于单光子态的苛刻要求,研究了采用标记单光子态时的量子放大的效果.数值模拟表明,采用移位算符的放大器比采用压缩的放大器具有更大的成功概率.
[1]CAO Dong,SONG Yaoliang,ZHU Cheng.A novel least-entanglement-assisted asymmetric quantum codes based on sliding grill[J].Chinese Journal of Electronics,2014,23(3):569-573.
[2]LI Jian,YE Xinxin,LI Ruifan,ZOU Yongzhong,LU Xiaofeng.Improved eavesdropping detection strategy based on extended three-particle Greenberger-Horne-Zeilinger state in two-step quantum direct communication protocol[J].Chinese Journal of Electronics,2012,21(4):736-739.
[3]ZHAO Wei,SAN Ye.Quantum-behaved particle swarm optimization algorithm with adaptive mutation based on q-Gaussian distribution[J].Chinese Journal of Electronics,2012,21(3):449-452.
[4]Ralph T C,Lund A P.Nondeterministic noiseless linear amplification of quantum systems[A].Proceedings of 9th International Conference on Quantum Communication Measurement and Computing[C].New York:AIP,2009.155-160.
[5]John Jeffers.Nondeterministic amplifier for two-photon superpositions[J].Physical Review A,2010,82(6):063828.
[6]Zavatta A,Fiuráek J,Bellini M.A high-fidelity noiseless amplifier for quantum light states[J].Nature Photonics,2011,(5):52-60.
[7]Guangsi Meng,Song Yang,et al.Noiseless suppression of losses in optical quantum communication with conventional on-off photon detectors[J].Physical Review A,2012,86(4):042305.
[8]Shengli Zhang,Song Yang,et al.Protecting single-photon entangled state from photon loss with noiseless linear amplification[J].Physical Review A,2012,86(3):034302.
[9]Jonatan Bohr Brask,Nicolas Brunner,et al.Bell tests for continuous-variable systems using hybrid measurements and heralded amplifiers[J].Physical Review A,2012,85(4):042116.
[10]Grosshans F,Grangier P.Continuous variable quantum cryptography using coherent states[J].Physical Review Letters,2002,88(5):057902.
[11]Rémi Blandino,Anthony Leverrier,et al.Improving the maximum transmission distance of continuous-variable quantum key distribution using a noiseless amplifier[J].Physical Review A,2012,86(1):012327.
[12]Jaromír Fiuráek,Nicolas J Cerf.Gaussian postselection and virtual noiseless amplification in continuous-variable quantum key distribution[J].Physical Review A,2012,86(6):060302(R).
[13]Xiang G Y,Ralph T C,et al.Heralded noiseless linear amplification and distillation of entanglement[J].Nature Photonics,2010,4(5):316-319.
[14]Mario A Usuga,Christian R Müller,et al.Noise-powered probabilistic concentration of phase information[J].Nature Physics,2010,6(10):767-771.
[15]Kocsis S,Xiang G Y,et al.Heralded noiseless amplification of a photon polarization qubit[J].Nature Physics,2013,9(1):23-28.
[16]Hong C K,Mandel L.Experimental realization of a localized one-photon state[J].Physical Review Letters,1986,56(2):58-60.
[17]Rarity J G,Tapster P R,Jakeman E.Observation of sub-poissonian light in parametric downconversion[J].Optics Communications,1987,63(3):201-206.
[18]Lvovsky A I,Hansen H,et al.Quantum state reconstruction of the single-photon fock state[J].Physical Review Letters,2001,87(5):050402.

王琨男,1990年3月出生,河南博爱人.解放军信息工程大学硕士研究生,主要研究方向为量子密码.
E-mail:jzwk351@163.com

郭建胜(通讯作者)男,1972年4月出生,河南沁阳人,教授、博士生导师.2004年获解放军信息工程大学博士学位,主要研究方向为信息安全.
E-mail:tsg-31@126.com
Research on Displacement-Assisted Quantum Linear Amplifiers
WANG Kun1,GUO Jian-sheng1,2,ZHANG Sheng-li1
(1.The PLA Information Engineering University,Zhengzhou,Henan 450004,China; 2.Science and Technology on Information Assurance Laboratory,Beijing 100000,China)
Quantum linear amplifier is an important tool to enhance already-known quantum communications.It can be used to protect the quantum state against photon loss.However,the gain and the probability of success in amplification is quite low.To this point,we propose to use coherent displacement operations to enhance quantum linear amplifiers.We derive the exact threshold beyond which local displacement helps to enhance distillation.We apply our state transfer theorem and numerically evaluate the dependence of quantum linear amplifiers gain on the amounts of displacement.
quantum optics;quantum displacement operations;quantum linear amplifier
2015-01-27;
2015-08-13;责任编辑:孙瑶
博士后科学基金(No.2014M562582)
TN918.1
A
0372-2112 (2016)07-1587-05
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.07.010
