保持粒子多样性的非退化粒子滤波方法研究

吴　昊，孙晓燕，郭玉堂，刘路路，沈　晶

(1.中国矿业大学信息与电气工程学院，江苏徐州 221008； 2.合肥师范学院计算机学院,安徽合肥 230601)

保持粒子多样性的非退化粒子滤波方法研究

吴昊1,2，孙晓燕1，郭玉堂2，刘路路2，沈晶2

(1.中国矿业大学信息与电气工程学院，江苏徐州 221008； 2.合肥师范学院计算机学院,安徽合肥 230601)

针对现有粒子滤波算法中的粒子退化问题以及重采样所引起的粒子多样性减弱问题，将自适应遗传算法与粒子滤波结合设计一种新的非退化粒子滤波算法.该算法通过对粒子使用遗传算子操作以保证粒子的多样性和有效性，根据粒子在前一时刻计算出来的先验信息自适应地实时调节当前时刻的遗传操作概率，有效增加了粒子对系统状态变化的适应性.实验结果表明，该算法可有效提高非线性系统状态的估计精度，尤其在系统状态发生突变的时候，可以得到较好的估计精度.

粒子滤波；遗传算法；粒子退化；自适应；粒子多样性

1　引言

粒子滤波PF[1～3](Particle Filter)是一种用于解决非线性滤波问题的滤波器.自上世纪70年代以来，解决非线性滤波问题最经典的是卡尔曼滤波(Kalman Filter,KF)以及寅生的扩展卡尔曼滤波(Extended Kalman Filter,EKF)、无香卡尔曼滤波(Unscented Kalman Filter,UKF)等，但是所有这些方法都依赖于高斯假设，但实际场合往往受环境影响，大部分不服从高斯分布.还有一种长解决非线性滤波问题的叫蒙特卡罗算法，但其存在严重的样本权值退化问题，直到1993年，Gordon等人[1]将重采样技术(Sampling Importance Resampling,SIR算法)引入蒙特卡罗重要性采样过程，提出一种自举滤波器，有效地解决了样本权值退化问题，即正则化粒子滤波算法(Regularized Particle Filter,RPF)；1999年，Carpenter等人[4]通过对这一类重采样算法进行概括总结，首次提出粒子滤波器的概念以及较著名的改进算法，如辅助粒子滤波器[5](Auxiliary Particle Filter,APF)、Unscented粒子滤波器[6](Unscented Particle Filter,UPF)、带进化选择的GF算法[7]、S-AGA算法[8]等.

当前，粒子滤波还普遍存在着粒子退化问题[9]、粒子多样性保持问题、运算时间较长等问题.如文献[1]RPF算法虽然可以部分解决粒子退化问题，但同时也降低了粒子多样性，使得系统状态在发生剧烈变化的时候难以得到正确的估计.文献[10]提出一种部分分层的重采样算法，可以快速完成重采样步骤，节省时间耗费，但同时也降低了粒子多样性.自适应类粒子滤波算法[11]，重采样需要通过在线计算并监视特定的有效样本量来确定，Moral等人[12]针对这类自适应重采样策略及其收敛性进行了详细的分析，但频繁的重采样使得粒子的多样性同样无法得到保持.左军毅等人[13]提出了一种自适应的部分重采样方法，这种改进方法实际上是在退化现象和多样性之间做了适度的折中.文献[14]提出一种改进的重采样方法，即灵敏重采样算法，该算法能够保持样本的多样性，提高粒子滤波算法的估计准确性.但是，该算法增加了计算时间.Li[15]等人提出了一种确定性重采样方法，但该方法只能在低维状态空间的状态估计问题中取得相对准确的结果.当前，引入基于生物遗传进化机制的采样方法也是研究热点，Xu[16]、Zhong等人[17]采用蚁群优化算法改进了粒子滤波算法，但二者工作不同，Zhong等人在计算粒子权值之前使用蚁群算法对粒子进行优化，并在文献[18]中提供了算法的理论证明，这种策略虽然可以解决样本多样性问题，但存在重采样步骤，且没有考虑粒子的先验信息，算法时间开销增大，效果不理想.

通过以上综述发现，当前的研究都在追求粒子滤波的多样性保持、粒子的非退化以及计算性能之间的平衡.本文构造一种新的基于自适应遗传算法的非退化粒子滤波方法，其基本思想是将前一时刻计算出来的粒子先验信息引入交叉变异等遗传操作，通过粒子的先验信息自适应调节遗传操作相关的概率参数，在充分考虑粒子先验信息的基础上，通过交叉变异等遗传操作来解决粒子的退化问题和多样性减弱的问题.

2　粒子滤波基本理论

2.1粒子滤波算法基本原理

(1)

根据这一近似，可将复杂的积分运算转化为求和运算，如兴趣函数g(x0:k)的数学期望式如下：

E(g(x0:k))=∫g(x0;k)p(x0;k|z1;k)dx0;k

(2)

基于样本的近似求解公式为：

(3)

在实际应用中，解决这一问题是通过引入重要性采样原则，用一种重要性采样密度q(x0:k|z1:k)来抽取样本，如此式(2)可以推导如下：

E(g(x0:k))=∫g(x0:k)p(x0:k|z1:k)dx0:k

=∫g(x0:k)ω*(x0:k)q(x0:k|z1:k)dx0:k

=Eq(·)[g(x0:k)ω*(x0:k)]

(4)

从重要性采样密度独立抽取N个样本粒子可得：

(5)

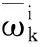
(6)

在k-1时刻，其递归的计算方法，可以将重要密度函数分解为以下形式：

q(x0:k|z1:k)=q(xk|x0:k-1,z1:k)q(x0:k-1|z1:k-1)

(7)

p(x0:k|z1:k)=

p(zk|xk)*p(xk|xk-m:k-1,z1:k-1)p(x0:k-1|z1:k-1)

(8)

并且式(7)也可写为如下形式：

q(x0:k|z1:k)=q(xk|xk-m:k-1,zk)q(x0:k-1|z1:k-1)

(9)

将式(7)和式(8)代入式(6)

(10)

选择合适的重要性采样密度q(·)可以递归计算更新粒子的权值，后验滤波密度可以近似为：

(11)

根据以上分析，可总结m阶粒子滤波的算法流程图如图1所示.

2.2基本方法评价

本节通过一个仿真实例来比较EKF算法与PF算法对非线性系统的估计效果.假设当前的状态系统如式(12)和(13)：

(12)

(13)

其中，粒子数为N为100，迭代次数T为60次，ωk和νk是独立的高斯白噪声，则系统的均方根误差为：

(14)

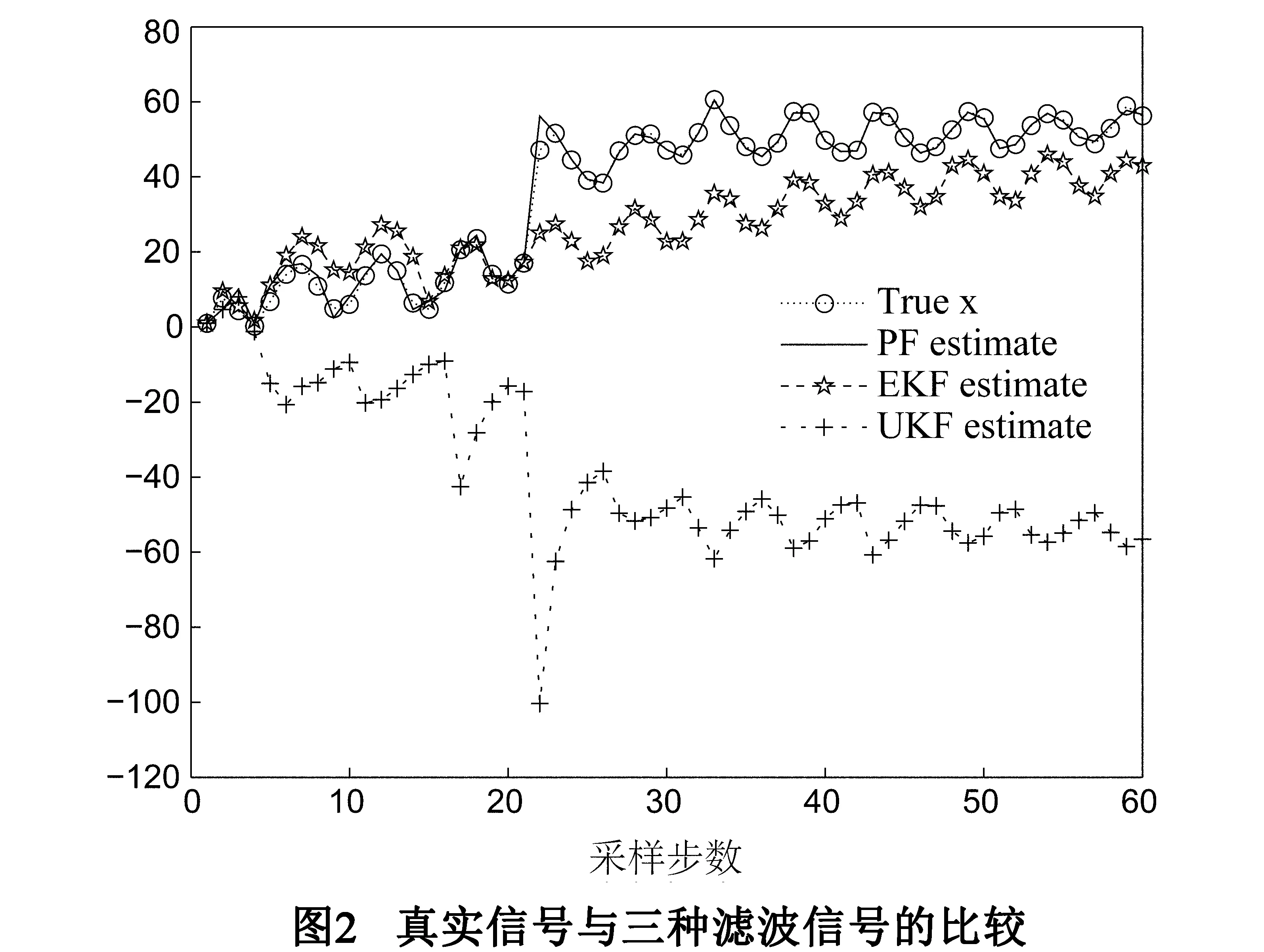
实验对此系统进行EKF、UKF和PF三种常见方法来状态的估计，结果如图2所示，可以看出UKF比EKF精度更好，说明EKF仅简单线性化非线性函数到一级泰勒级数展开，因而引入了额外的误差导致滤波精度降低.PF的估计效果，特别是在迭代次数20次以内，较两者都好很多.EKF、UKF、PF算法的均方误差值RMSE分别为99.0241、97.7673、18.9468，由此也可以看出PF具有较好的拟合度.

3　自适应遗传算法

遗传算法是由美国的Holland教授1975年在他的专著《自然界和人工系统的适应性》[19]中首先提出的，标准遗传算法基本思想如下[19]：

首先随机产生一组初始个体构成的初始种群，并评价每一个个体的适应度值f；接着判断算法是否满足收敛准则，若满足输出最优结果，否则执行以下步骤；在根据适应度值的大小以一定的方式执行个体的选择操作；在按事先确定的交叉概率pc、变异概率pm执行交叉变异操作；后返回到判断是否满足收敛准则，不满足继续进行遗传操作，直至满足退出条件.

此算法的交叉、变异概率一定，这可能会导致其存在早熟以及收敛速度慢[20].许多学者对此进行了系统的研究.文献[21]中用模糊规则对选择概率和变异概率进行控制，在线改变其值.文献[22]利用云模型云滴的随机性和稳定倾向性特点，由条件发生器产生交叉概率和变异概率.文献[11]是一种常用自适应遗传算法(S-AGA)，其核心思想是通过个体的适应度函数值来确定交叉概率pc和变异概率pm，具体的计算公式如下：

(15)

(16)

式中，k1=k3=1,k2=k4=0.5,fmax是种群中最大适应度值，f ′是两个交叉个体中较大的适应度值，favg是种群适应度的平均值，f是变异个体的适应度值.算法的不足在于过分的保护了种群中的优势个体，而无法产生新的优势个体，即早熟现象.

4　本文的非退化粒子滤波算法

本文算法将遗传算法内嵌到粒子滤波算法中，其基本思路是先采样得到一组粒子，然后通过遗传算法的选择、交叉、变异等操作来得到一组新的粒子，用于计算系统状态的估计值.算法结构如图3所示.

第二步：遗传操作.

(1)选择：首先要对采样的粒子集合重新进行适应度评估，并对所有粒子的权值进行归一化处理，将粒子的权值作为个体的适应度函数值，即：

(17)

(2)交叉和变异：对于文献[23]的早熟现象，为保证高适应度的个体也需要保持一定的交叉概率，以增加新产生的子代个体中优秀个体的数量，对于适应度高于平均值的个体，使用式(18)中的指数函数形式对个体的交叉概率进行调节，使个体的交叉概率最终下降到某一固定的数值，从而保证最优的那部分个体可以保持一定的交叉概率.对于适应度高于平均值的个体，使用式(19)中的指数函数对个体的变异概率进行调节，使得个体的变异概率快速的呈指数下降，更有利于保护种群中的优势个体不受破坏.

(18)

(19)

pc1,pc2,pm1,pm2分别表示pc和pm的变化范围.文献[23]中可知，个体交叉概率、变异概率的变化范围分别为[0.5，1]、[0.001，0.05]，在这个区间里，设pc2,pm2一定，然后取不同的pc1,pm1值通过试验结果找到其最佳值，本文分别取0.95、0.07.

图4、图5反映了新算法在交叉操作中，适应度值较高的优秀个体保持了一定的交叉概率pc以产生更多优秀子代；变异过程中的高适应度个体加速了变异概率pm的降低速度，优秀个体得到保护.

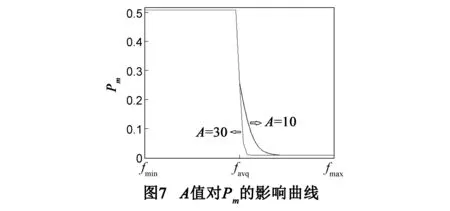
常数A在适应度值高于平均水平时可对pc和pm的变化趋势进行调节，当系数pc1,pc2,pm1,pm2确定时，常数A的取值可调节pc和pm进行自适应调节的范围.当A取值较大时，交叉概率pc和变异概率pm自适应调节的范围较小，且随着个体适应度的增大而使得pc快速变小.而当A的取值较小的时候，可相应的扩大pc和pm调节的范围，并减缓了pc和pm下降的速度.图6、图7给出当系数pc1,pc2,pm1,pm2一定时，A取不同值对pc和pm变化的影响.表1给出了多次试验参数取值不同时的均值误差.A的数值是由多次实验估计效果得到当pc1=0.95，pc2=0.5，pm1=0.07，pm2=0.001时，取A=9.9034时，算法可取得较好的实验结果.

第三步：将通过遗传操作得到的新的种群进行下一次采样.

表1　本文算法取不同数对时估计误差的均值表

5　实验结果与分析

实验选取三个模型，即一维非平稳经济学估计问题、二维目标跟踪模型、高维的Truck-Trailer系统跟踪问题.

5.1一维模型(非平稳经济学估计问题)

这种模型的特点是具有高度非线性和双峰的特性.其状态方程和量测方程如下：

(20)

(21)

其中c1，c2和c3是系统预定义常量，高斯噪声μk，νk相互独立.实验取c1=1，c2=12，c3=7，x0=0，pc1=0.95，pc2=0.5，pm1=0.07，pm2=0.001，A=9.9034.本文算法分别和APF、RPF、以及文献[11]中提出的GA-MCMC算法在加跳变和不加跳变二种情况下的估计效果进行比较.实验独立做20次.

图8、图9分别为二种实验的截图.定性可以看到，无跳变时各种算法的效果基本都很好，但在一些状态发生一定变化的时刻，本文算法的估计精度更高，效果更好.第二种情况，在实验中当迭代次数k=50时刻人为加上剧烈跳变，此时可以从图9看出，APF算法对系统状态的估计能力最差，RPF和文献[11]算法在状态发生巨变的同时也都不能及时对状态做出准确的估计，需要经过一段时间的调整之后才可对系统状态进行准确的估计，本文算法在系统状态发生剧变的情况下依然能够保持对而系统状态的良好的估计，其算法中对粒子交叉概率和变异概率的调整策略，要优于文献[11]算法，本文算法与真实状态的拟合度要比其他几种算法要好很多，有着更好地估计效果.表2、表3中给出两种情况下分别取不同的粒子数时进行的20次独立实验中RMSE的均值、最小值、最大值以及运行时间.

由重要性采样定理[1]可知，当粒子数增大时，粒子集更能接近系统的真实状态，如表2、表3所示.然而粒子集的增大必然会增大系统的时间复杂度，进而影响算法的实时性和逼近效果.因此，实验根据假设检验，动态确定粒子数目，在保证算法效果的同时降低算法的时间复杂度，从而达到更好的时间性能.

表2　无跳变情况算法RMSE均值、Min、Max值及时间比较

表3　有跳变情况算法RMSE均值、Min、Max值及时间比较

设H0表示估计状态下μ等于真实状态μ0，拒绝域H1为目标估计状态下μ不等于真实状态μ0.由双边检验问题可以求得：

(22)

实验设定显著性水平参数α，犯第Ⅱ类错误的概率β的值都取0.05.由此可得粒子数样本容量n满足：

(23)

通过表2、表3的数据，带入式(23)，可知，事实上，粒子数在100时，对于给定的显著水平，就能够很好地接受原假设，具有较好的估计精度.

5.2二维模型(目标跟踪模型)

实验选取常用的模型同文献[23]一致，运动模型与观测模型如式(24)和(25)所示：

xk=Φxk-1+Γwk

(24)

zk=tan-1(yk/xk)+vk

(25)

在二维模型中，vx，vy的状态只与自身前一时刻的状态有关，而x和y的状态除与自身状态有关外，还与vx，vy的状态有关，变化的复杂度较高.由于观测值的确定只与x和y有关，因此，只对其状态中的x和y分量进行操作.

实验设计二种情况，即系统状态未发生跳变以及系统状态发生跳变.二种情况下，本文算法分别于APF、RPF、GF、S-AGA、文献[11]算法进行比较.估计效果如图10、图11所示.从图10可以看出无跳变情况下本文算法相对于GF、APF、RPF也有较好的的估计精度，本质原因是算法在粒子重采样以后失去了多样性；如图10(c)对于S-AGA、文献[11]算法，本文算法也有着一定的优越性.从图11可以看出，在系统状态发生跳变时，APF、RPF、GF算法基本没有粒子分布在真实状态的周围，估计误差较大，同样也是粒子退化问题以及多样性无法保持而影响到估计精度.S-AGA、文献[11]算法虽然也对粒子的遗传操作概率进行调整，然而没有考虑重要性权重的先验信息，因此对真实状态逼近的有效性也有较大的误差.本文算法通过对粒子权重先验信息的考虑，自适应调节交叉、变异的概率，与其他算法相比较，特别是遇到剧烈跳变时其滤波精度有了较大的提高.

5.3高维模型(卡车-拖车(Truck-Trailer)系统的跟踪问题)

实验选取带有拖车的卡车的运动轨迹进行跟踪，在这一系统中拖车的节数越多，估计系统的维数就越高.本文设定卡车后带有一节拖车，状态空间可用如下式(26)到式(31)来表示.由公式中可以看出，该系统是由4维变量组成的状态系统，在图12中给出该系统的示意图.其w为卡车的长度，L为拖车的长度，T为采样周期，v为卡车的速度，u(x)为用于控制输入的转向角，x0(k)为卡车的角度，x1(k)为卡车与第一节拖车的角度差，x2(k)为第一节拖车的角度，x3(k)为第一节拖车的垂直位置，x4(k)为第一节拖车的水平位置.

(26)

x1(k)=x0(k)-x2(k)

(27)

(28)

+ω3(k)

(29)

+ω4(k)

(30)

(31)

这里假设卡车和拖车快速移动的过程中，观测值在短时间发生了较大的变化而形成了跳变.而后使用各种算法对该系统的跟踪情况进行比较.在该部分的试验中，统一使用的粒子个数为300，转移噪声和观测噪声的协方差矩阵分别Q=diag(12,12,12,12)，R=diag(12,12,12,12).该系统中有5个变量.由于篇幅，实验只选取系统发生跳变的情况下进行，图13给出了各个算法对变量x4的跟踪效果比较，表4给出其余变量20次估计结果的RMSE平均值.

从图13可以看出本文算法的估计精度要明显优于SIR、APF、RPF，这些算法大都在迭代次数50次左右时就失去了跟踪性能.SIR算法在粒子重采样以后无法保持其多样性，在状态发生剧变时由于没有粒子分布在真实状态的周围而导致跟踪失败，APF和RPF算法并且还缺乏对解决粒子的退化问题的有效考虑.

表4　高维模型系统状态跳变时各种算法估计结果RMSE均值比较

本文算法在遇到跳变时，由于遗传策略具有更好地全局寻优能力，其跟踪效果也有很大的改进.从表4的均方根误差定量分析来看，相比其他算法本文改进的自适应粒子滤波算法能够更好地地拟合真实状态，保证了更好地跟踪效果.

6　结论

本文设计一种基于自适应粒子滤波算法，算法利用粒子的先验信息确定粒子的适应度值，通过粒子的适应度值自适应确定该粒子进行交叉、变异的概率，解决来粒子的有效性与多样性的问题.该方法充分利用了粒子的先验信息，因而增加了粒子对系统状态变化的适应性，有效提高了对系统状态的估计精度.实验分别选取一维、二维以及高维的非线性数据模型进行仿真，结果表明该算法可有效提高非线性系统状态的跟踪效果，特别在实验时，人工加上剧烈跳变，本文算法与其它粒子滤波算法相比更具有优越性.

[1]Arulampalam S,Maskell S,Gordon N,et al.A tutorial on particle filters for online nonlinear/nonGaussian Bayesian tracking[J].IEEE Trans Signal Process,1993,140(2):107-113.

[2]王法胜,等.粒子滤波算法[J].计算机学报,2014,37(8):1679-1694.

Wang Fasheng,et al.Particle filter algorithm[J].Chinese Journal of Computers,2014,37(8):1679-1694.(in Chinese)

[3]Sarkka S.Bayesian Filtering and Smoothing[M].Cambridge：Cambridge University Press,2013.

[4]Carpenter J,Clifford P,Fearnhead P.Improved particle filter for non-linear problems[J].IEE Proceedings-Redar,Sonar and Navigation,1999,146(1):2-7.

[5]Pitt M,Shephard N.Auxiliary particle filters[J].Journal of The American Statistical Association,1999,94(446):590-599.

[6]Merwe R,et al.The unscented particle filter[R].Cambridge University Engineering Department CUED/F-INFENG/TR 380.England:Cambridge University Press,2000.1-45.

[7]Park S,Hwang J,et al.A new particle filter inspired by biological evolution:Genetic filter[J].International Journal of Applied Science Engineering and Technology,2007,4(1):459-463.

[8]Srinivas M,Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Transactions on Systems,Man and Cybernetics,1994,24(4):656-667.

[9]Djuric P,Bugallo M,Mahesh B.Target Tracking by Particle Filtering in Binary Sensor Networks[J].IEEE Transactions on Signal Processing,2008,56(6):2229-2238.

[10]Yu J,Tang Y,Liu W.An improved resampling algorithm in particle filter[J].Journal of Computational Information Systems,2010,6(2):629-635.

[11]LI CY,JI HB.A new particle filter with GA-MCMC resampling[A].Proceedings of International Conference on Wavelet Analysis and Pattern Recognition[C].Beijing,China,2007.146-150.

[12]Moral P,Doucet A,Jasra A.On adaptive resampling strategies for sequential Monte Carlo methods[J].Bernoulli,2012,18(1):252-278.

[13]左军毅，张怡哲，梁彦.自适应不完全重采样粒子滤器[J].自动化学报，2012，38(4)：647-652.

Zuo Junyi,Zhang Yizhe,Liang Yan.Particle filter based on adaptive part resampling[J].Acta Automatica Sinica,2012,38(4):647-652.(in Chinese)

[14]Gordon N J,Salmond D J,Smith A F M.Novel approach to nonlinear non-Gaussian Bayesian state estimation[J].IEEE Proceedings on Radar,Sonar and Navigation,1993,140(2):107-113.

[15]Li T，Sattar T，Sun S.Deterministic resampling：Unbiased sampling to avoids ample impoverishment in particle filters[J].Signal Processing，2012，92(7)：1637-l645.

[16]Xu B，Chen Q，et al.Ant estimator with application to target tracking[J].Signal Processing，2010，90(5)：1496-1509.

[17]Zhong J,Fung Y,Dai M.A biologically inspired improvement strategy for particle filter：Ant colony optimization assisted particle filter[J].International Journal of Control，Automation，and Systems,2010,8(3):519-526.

[18]Zhong J,Fung Y.Case study and proofs of ant colony optimization improved particle filter algorithm[J].IET Control and Applications,2012,6(5):689-697.

[19]戴朝华，朱云芳，陈维荣.云自适应遗传算法[J].控制理论与应用，2007，24(4):646-650.

Dai Chaohua,Zhu Yunfang,Chen Weirong.Adaptive genetic algorithm based on cloud theory[J].Control Theory and Applications,2007,24(4):646-650.(in Chinese)

[20]张铃，张钹.遗传算法机理的研究[J].软件学报,2000，11(7)：945-952.

Zhang Ling,Zhang Bo.Research on the mechanism of genetic algorithms[J].Journal of Software,11(7):945-952.(in Chinese)

[21]刘莉，陈学允.基于模糊遗传算法的配电网络重构[J].中国电机工程学报，2000,20(2)：66-69.

Liu Li,Chen Xueyun.Reconfiguration of distribution networks based on fuzzy genetic algorithms[J].Proceedings of the Chinese Society of Electrical Engineering,2000,20(2):66-69.(in Chinese)

[22]HOLLAND J H.Adaptation in Natural and Artificial Systems:An Introductory Analysis with Applications to Biology,Control and Artificial Intelligence (2nd ed)[M].Cambridge:MIT Press,1992.

[23]Fu X,Jia Y.An improvement on resampling algorithm of particle filters[J].IEEE Transactions on Signal Processing，2010，58(10)：5414-5420.

吴昊男,1983年5月出生，安徽舒城人.合肥师范学院讲师，2010硕士毕业于合肥工业大学，2015年进入中国矿业大学，博士生，从事图像处理、优化算法方面的有关研究.

E-mail:dillon-wu@126.com

孙晓燕女,1978年10月出生，江苏丰县人.教授、博士生导师、IEEE高级会员.从事进化优化算法及应用、多目标进化算法设计和机器学习等方面的工作.

E-mail:xysun78@126.com

Non-Degeneracy Particle Filtering Method Research forParticle Diversity Preserving

WU Hao1,2,SUN Xiao-yan1,GUO Yu-tang2,LIU Lu-lu2,SHEN Jing2

(1.School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou,Jiangsu 221008,China; 2.School of Computer Science and Technology,Hefei Normal University,Hefei,Anhui 230601,China)

To cope with the degeneracy in the existing particle filter algorithm and the diversity weakening caused by re-sampling,a new non-degeneracy algorithm is proposed in this paper by incorporating adaptive genetic algorithm into particle filter.By using genetic operators to generate new particles,the algorithm can adjust the current probability of genetic manipulation adaptively based on the previously calculated information so that the diversity and effectiveness of the particle can be ensured.It effectively improves the adaptability of particle to the changes of the system state.Experimental results show that this algorithm can effectively improve the estimation accuracy of the nonlinear system state.In particular,the algorithm can guarantee good estimation accuracy when the system state changes abruptly.

particle filter;genetic algorithm;particle degeneracy;adaptive;diversity of particle

2015-01-28；

2015-08-10；责任编辑：李勇锋

国家自然科学基金(No.61301062,No.61503116,No.61375067)；中央高校基本科研业务经费(No.2012QNA58)；安徽省高校自然基金(No.KJ2013A217)；安徽省质量工程提升计划(No.2013zy058)；安徽省教育厅高等学校省级优秀青年人才基金(No.SQRL129ZD)

TP18

A

0372-2112 (2016)07-1734-08

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.07.031