抗脉冲干扰的分布式仿射投影符号算法

倪锦根,马兰申

(苏州大学电子信息学院,江苏苏州 215006)

抗脉冲干扰的分布式仿射投影符号算法

倪锦根,马兰申

(苏州大学电子信息学院,江苏苏州 215006)

递增式和扩散式仿射投影算法收敛较快,但在脉冲噪声环境下这两种分布式估计算法收敛性较差或容易发散.本文采用受网络节点的权值向量更新约束的后验误差向量l1范数最小化方法,提出了两种抗脉冲干扰的分布式估计算法,即递增式和扩散式仿射投影符号算法.仿真结果表明,与分布式仿射投影算法相比,分布式仿射投影符号算法在脉冲噪声环境下具有更好的鲁棒性.

自适应网络;仿射投影;符号算法;分布式估计

1　引言

随着信息科学与技术的迅速发展,网络在日常生活、工业生产、航空航天等领域具有广泛的应用.目前,网络的分类方式较多:按照是否需要物理方式连接,可将网络分为有线网络和无线网络;按照网络节点信息的传递方式,可将网络分为总线型、星型和环形等网络.通常将节点分散放置在某个特定区域上,且每个节点具有一定信息处理能力的网络称为分布式网络[1].分布式网络在目标跟踪[2]、动物群体运动模拟[3]、基因网络建模[4]、频谱感知[5]等领域具有重要作用.自适应网络是对具有自适应信号处理能力的分布式网络的总称.能够对网络节点采集到的信息进行分析和推理,且自适应地估计某个感兴趣参量的分布式网络,都可以称为自适应网络[6],并将对自适应网络的参数进行估计的算法称为分布式估计算法.

由于分布式网络使用广泛,近年来学者们对分布式估计的研究产生了极大的兴趣,提出了一系列分布式估计算法.典型的分布式估计算法主要包括递增式和扩散式最小均方算法(分别简记为ILMS和DLMS)[7,8]、递增式和扩散式递归最小二乘算法(分别简记为IRLS和DRLS)[9,10]、递增式和扩散式仿射投影算法(分别简记为IAPA和DAPA)[11,12].此外,学者们还提出了加快估计稀疏未知向量的分布式估计算法[13,14]和基于信息论准则的分布式估计算法[15].递增式和扩散式最小均方算法因实现简单、计算复杂度低等优点,成为应用较多的两种分布式估计算法,但其缺点是收敛速度较慢.递增式和扩散式递归最小二乘算法能够加快分布式估计的收敛速度,但其计算复杂度高,跟踪能力差.递增式和扩散式仿射投影算法的收敛速度快于递增式和扩散式最小均方算法,且计算复杂度低于递增式和扩散式递归最小二乘算法,因而具有很好的实用性.

自适应滤波算法的鲁棒性通常用来指自适应滤波算法的抗大噪声干扰能力.大部分文献假设分布式网络的所有节点都处于较小的噪声环境中[7～14].在这类环境中,上述算法一般不存在鲁棒性问题.然而在有些情况下,网络所处的环境非常恶劣,网络节点采集到的信号很可能收到脉冲噪声的干扰.到目前为止,大部分分布式估计算法是基于l2范数最优化方法建立的.在脉冲噪声环境中,网络节点的输出误差信号中包含了脉冲噪声.脉冲噪声的幅值通常是输出误差信号中所包含的有用信号幅值的几百甚至几千倍.基于l2范数的分布式估计算法直接使用包含脉冲噪声的输出误差信号去更新节点的权值向量,因而收敛性较差,甚至发散.已有研究结果表明,基于l1范数最优化方法建立的自适应滤波算法具有很好的鲁棒性,如基于最小均方算法的符号算法(简记为SA)[16]、基于混合范数最优化的符号算法(简记为MSA)[17]、仿射投影符号算法(简记为APSA)[18,19]等,其中仿射投影符号算法具有最快的收敛速度.

为了解决已有分布式估计算法抗脉冲干扰能力差这一问题,本文提出了两种分布式估计算法,即递增式和扩散式仿射投影符号算法.与文献[11,12]中采用牛顿迭代法推导递增式和扩散式仿射投影算法不同,本文首先建立受条件约束的后验误差向量l1范数最小化公式,然后采用拉格朗日乘子法来推导递增式和扩散式仿射投影符号算法.仿真结果表明,与文献[11,12]中提出的递增式和扩散式仿射投影算法相比,递增式和扩散式仿射投影符号算法在脉冲噪声环境下具有更好的鲁棒性.在户外勘探、环境监测以及军事等领域,网络节点所处的环境较为恶劣,如在人类较难进入的大山或者森林中.在这些环境中,网络节点可能会受到雷电或强电磁波的干扰.本文提出的分布式估计算法具有很好的抗脉冲干扰能力,因而在上述环境中具有很好的应用前景.

2　自适应网络模型

自适应网络的拓扑结构也称为自适应网络的协作模式.目前,自适应网络的协作模式主要分为三类[6],即递增式协作模式、扩散式协作模式和概率扩散式协作模式,如图1所示.在递增式协作模式中,网络节点信号按顺序从一个节点传递到与之相邻的下一个节点,因此,这种协作模式所需的通信量最低,但网络节点间必须构成一个通信环路.在扩散式协作模式中,每个节点与其邻域内的节点进行通信,因此,这种协作模式的通信量大于递增式自适应网络,但这种协作方式能够充分利用其邻域内节点包含的信息,且无需在节点间构建通信环路.在概率扩散式协作模式中,各节点的工作方式与在扩散式协作模式中的工作方式类似,但每个节点的邻域不是固定的,即节点之间以一定的概率进行连接(图中用虚线表示依概率连接),因而具有更好的灵活性,但连接方式实现更加复杂.本文主要讨论递增式和扩散式协作模式.

3　分布式估计算法推导

将节点n的L阶投影输入矩阵和期望向量分别记为

Un(k)=[un(k),un(k-1),…,un(k-L+1)]

(1)

dn(k)=[dn(k),dn(k-1),…,dn(k-L+1)]T

(2)

定义节点n的先验和后验误差向量分别为

(3)

(4)

其中,wn(k)表示节点n对未知向量wo在k时刻的估计.文献[8]提出了一种用于自适应滤波器的仿射投影符号算法,该算法对脉冲噪声干扰具有很好的鲁棒性.本文将该算法进行推广,提出两种分布式仿射投影符号算法.

建立如下受条件约束的最小化公式:

(5)

(6)

其中,‖·‖1和‖·‖2分别表示取l1和l2范数,μn为节点n的步长参数,g(n,k)表示与变量n、变量k相关的对未知向量wo的一个估计值,对该向量采用不同的取值方式将获得不同的分布式估计算法.采用式(5)和式(6)来推导鲁棒的分布式估计算法的依据如下:在式(5)中,最小化后验误差向量的l1范数可以使得每个节点的权值向量沿着使代价函数减小的方向移动,从而逼近未知向量,且l1范数最小化使得权值向量更新公式中只包含误差信号的符号运算,因而可以降低脉冲噪声干扰对节点的影响[17];式(6)中的约束条件能够通过步长μ限定算法每次迭代的幅度,从而防止算法发散.

为了采用拉格朗日乘子法求解上述受约束的最优化问题[18],建立如下的代价函数

(7)

∂J(k)/∂wn(k)

=-Un(k)sgn[εn(k)]+2λn[wn(k)-g(n,k)]

(8)

令上式为零,可得

(9)

将式(9)代入式(6)并取等号,从而有

(10)

上式可变换为

(11)

将式(11)代入式(9),可得wn(k)=g(n,k)

(12)

上式中添加的δ为很小的正常数,用来避免数值计算困难,文献中称其为正则化因子.

3.1递增式仿射投影符号算法

令g(n,k)=wn-1(k),则式(12)转化为

wn(k)=wn-1(k)

(13)

wn(k)=wn(k-1)

(14)

由式(14)可见,网络中各节点间的信号传递方式符合图1(a)所示的递增式协作模式,即各节点之间按顺序从前往后传递信号.为了形成通信环路,可将最后一个节点N在k-1时刻的结果作为起始节点1在k时刻更新的基础,即递增式仿射投影符号算法的权值向量更新可表示为

(15)

在递增式协作模式中,每个节点只需要和相邻的前后两个节点间进行通信,因而能够降低每个节点需要的功耗.如果网络中某个节点出现故障,那么整个网络就会因链路断裂而无法正常工作.下面将要介绍的扩散式仿射投影符号算法可以解决这一问题.

3.2扩散式仿射投影符号算法

在图1(b)所示的扩散式协作模式中,将能够与节点n进行通信的所有节点(包括该节点n本身)形成的集合称为节点n的邻域Nn.每个节点n通过与其邻域内其他节点通信来获得它们在k-1时刻对未知向量的估计{wi(k-1);i∈Nn},然后通过特定的联合方式来生成节点n对未知向量wo在k-1时刻的中间估计φn(k-1)=fn[wi(k-1)], i∈Nn,其中fn[·]表示节点n的联合函数[8].该中间估计最终作为节点n在k时刻更新的基础.

令g(n,k)=φn(k-1),则式(11)转化为

wn(k)=φn(k-1)

(16)

wn(k)=φn(k-1)

(17)

如果用线性组合来表示联合函数fn[·],则式(17)中的中间估计可表示为[8]

(18)

(19)

由式(19)可知,使用扩散式仿射投影符号算法,网络中每个节点的权值向量更新只需要传递其邻域中节点的信号.当邻域中某一节点因发生故障而无法通信时,可将与该节点相关的联合参数置零,并通过邻域中剩余的结点进行分布式估计.因此,该算法虽然增大了通信量,但比递增式仿射投影符号算法具有更好的稳定性.

4　实验结果与分析

网络中各节点的输入信号un(k)、高斯白噪声vn(k)和脉冲噪声θn(k)的方差如图3所示.输入信号un(k)由零均值的高斯白噪声通过一阶系统F(z)=1/(1-0.9z-1)产生,脉冲干扰θn(k)为伯努利-高斯过程,该过程由伯努利过程ωn(k)与零均值的高斯过程zn(k)相乘产生,即θn(k)=ωn(k)zn(k).伯努利过程ωn(k)的概率分布为:当ωn(k)=1时,P[ωn(k)]=Pr;当ωn(k)=0时,P[ωn(k)]=1-Pr.实验中将Pr取为0.01.由图3可见,每个节点n对应的脉冲噪声θn(k)的方差远大于高斯噪声vn(k)的方差.所有算法的投影阶数L都取为5,正则化因子δ都取为0.01.

图4为递增式仿射投影算法(IAPA)、仿射投影符号算法(APSA)和递增式仿射投影符号算法(IAPSA)的网络均方偏差曲线.为了比较APSA和IAPSA的收敛速度,我们将两种算法的步长μ分别取为0.008和0.01,从而获得相同的稳态失调.由该图可见,在存在脉冲干扰的情况下,IAPA收敛很慢(μ=0.0001)或者不收敛(μ=0.001),而IAPSA和APSA都能够收敛,且IAPSA比APSA收敛更快.

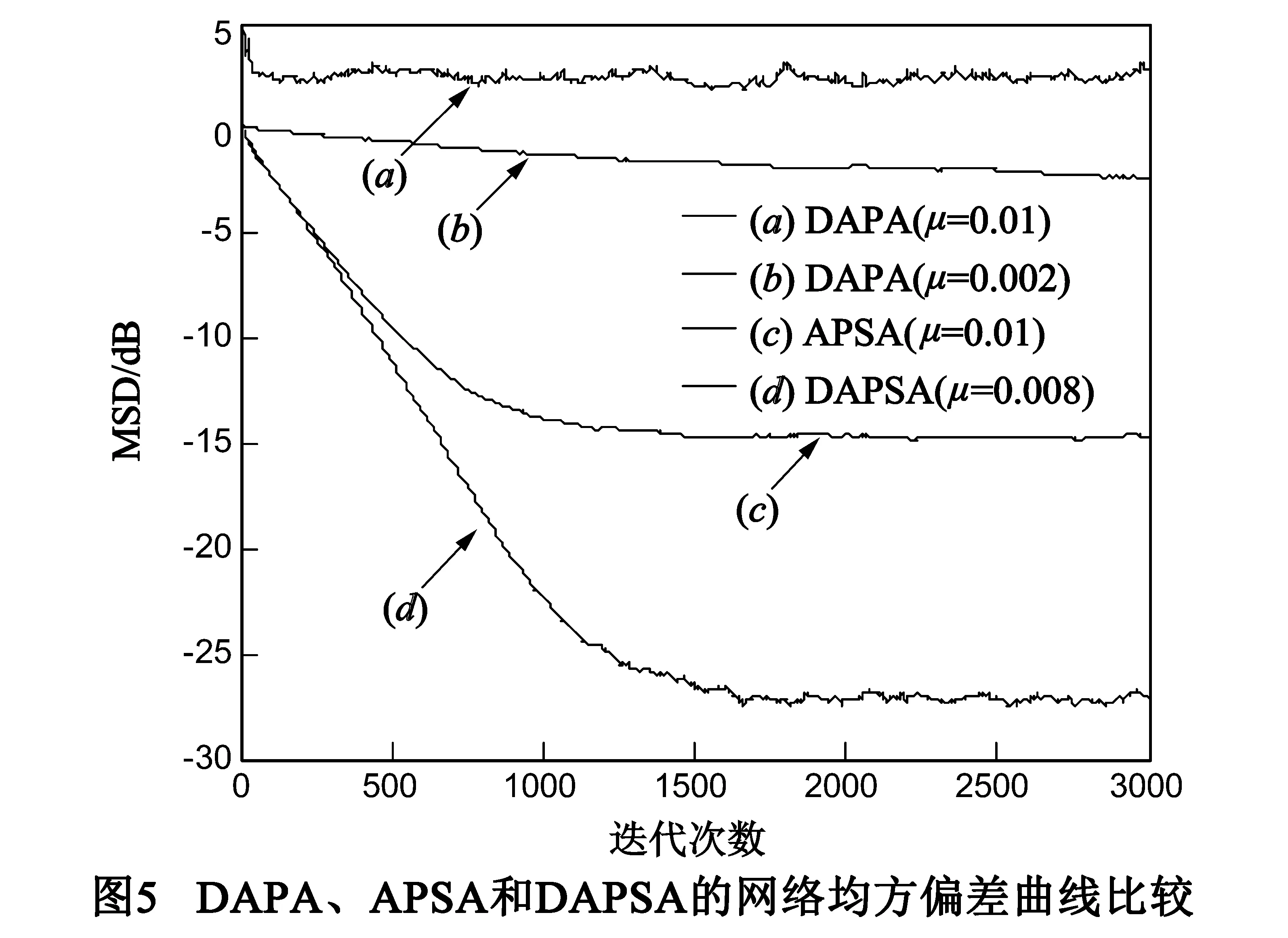
图5为扩散式仿射投影算法(DAPA)、仿射投影符号算法(APSA)和扩散式仿射投影符号算法(DAPSA)的网络均方偏差曲线图.为了比较APSA和DAPSA的稳态失调,我们将两种算法的步长μ分别取为0.01和0.008,从而达到相同的初始收敛速度.由该图可见,在存在脉冲干扰的情况下,DAPA收敛很慢(μ=0.002)或者不收敛(μ=0.01),而DAPSA和APSA都能够收敛,且DAPSA比APSA稳态失调更低.

5　结论

本文通过分布式网络中的递增式和扩散式协作模式,分别推导了两种分布式估计算法,即递增式与扩散式仿射投影符号算法.由于递增式与扩散式仿射投影符号算法都涉及符号运算,因此具有较低的计算复杂度.仿真结果表明,在脉冲噪声干扰的情况下,递增式和扩散式仿射投影符号算法比递增式和扩散式仿射投影算法具有更强的鲁棒性.

[1]Sayed A H.Adaptation,learning,and optimization over networks[J].Foundations and Trends in Machine Learning,2014,7(4-5):311-802.

[2]Tu S Y,Sayed A H.Mobile adaptive networks[J].IEEE Journal of Selected Topics in Signal Processing,2011,5(4):649-664.

[3]Lorenzo P Di,Barbarossa S,Sayed A H.Bio-inspired decentralized radio access based on swarming mechanisms over adaptive networks[J].IEEE Transactions on Signal Processing,2013,61(12):3183-3197.

[4]Shin Y J,Sayed A H,Shen X.Adaptive models for gene networks[J].Plos One,2012,7(2):e31657.

[5]Quan Z,Zhang W,Shellhammer S J,et al.Optimal spectral feature detection for spectrum sensing at very low SNR[J].IEEE Transactions on Communications,2011,59(1):201-212.

[6]Sayed A H.Adaptive network[J].Proceedings of the IEEE,2014,102(4):460-497.

[7]Lopes C G,Sayed A H.Incremental adaptive strategies over distributed networks[J].IEEE Transactions on Signal Processing,2007,55(8):4064-4077.

[8]Lopes C G,Sayed A H.Diffusion least-mean squares over adaptive networks:formulation and performance analysis[J].IEEE Transactions on Signal Processing,2008,56(7):3122-3136.

[9]Sayed A H,Lopes C G.Adaptive processing over distributed networks[J].IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences,2007,E90-A(8):1504-1510.

[10]Cattivelli F S,Lopes C G,Sayed A H.Diffusion recursive least-squares for distributed estimation over adaptive networks[J].IEEE Transactions on Signal Processing,2008,56(5):1865-1877.

[11]Li L,Chambers J A,Lopes C G,Sayed A H.Distributed estimation over an adaptive incremental network based on the affine projection algorithm[J].IEEE Transactions on Signal Processing,2010,58(1):151-164.

[12]李雷雷,何剑辉,张勇刚.分布式网络中的仿射投影自适应算法[J].中国传媒大学学报,2012,19(2):34-43.

LI Lei-lei,HE Jian-hui,ZHANG Yong-gang.Affine projection algorithms over distributed wireless networks[J].Journal of Communication University of China,2012,19(2):34-43. (in Chinese)

[13]Liu Y,Li C,Zhang Z.Diffusion sparse least-mean squares over networks[J].IEEE Transactions on Signal Processing,2012,60(8):4480-4485.

[14]Liu Z,Liu Y,Li C.Distributed sparse recursive least-squares over networks[J].IEEE Transactions on Signal Processing,2014,62(6):1386-1395.

[15]Li C,Shen P,Liu Y.Diffusion information theoretic learning for distributed estimation over network[J].IEEE Transactions on Signal Processing,2013,61(16):4011-4024.

[16]Sayed A H.Adaptive Filters[M].Hoboken,New Jersey:John Wiley & Sons,2008.

[17]Papoulis E V,Stathaki T.A normalized robust mixed-norm adaptive algorithm for system identification[J].IEEE Signal Processing Letters,2004,11(1):56-59.

[18]Shao T,Zheng Y R,Benesty J.An affine projection sign algorithm robust against impulsive interferences[J].IEEE Signal Processing Letters,2010,17(4):327-330.

[19]Ni J,Li F.Efficient implementation of the affine projection sign algorithm[J].IEEE Signal Processing Letters,2012,19(1):24-26.

[20]Ni J,Chen X,Yang J.Two variants of the sign subband adaptive filter with improved convergence rate[J].Signal Processing,2014,96(B):325-331.

倪锦根男,1979年11月生,江苏省兴化市人.毕业于复旦大学,获理学博士学位,现为苏州大学电子信息学院副教授、硕士生导师,IEEE会员.主要研究方向为自适应滤波、自适应网络、多采样率滤波器组设计、高速数字系统的FPGA实现.

E-mail:jni@suda.edu.cn

马兰申男,1988年4月生,安徽省亳州市人.获苏州大学硕士学位.研究方向为自适应滤波和分布式估计.

E-mail:malanlong@163.com

Distributed Affine Projection Sign Algorithms Against Impulsive Interferences

NI Jin-gen,MA Lan-shen

(School of Electronic and Information Engineering,Soochow University,Suzhou,Jiangsu 215006,China)

While the incremental and diffusion affine projection algorithms have fast convergence rate,they may suffer from bad convergence performance or divergence in impulsive interference environments. Based on the method of minimization of the l1-norm of the a posteriori error vectors subject to a constraint on the update of the weight vectors of nodes in the network,two distributed estimation algorithms against impulsive interferences are proposed,namely,the incremental and diffusion affine projection sign algorithms. Simulation results show that the distributed affine projection sign algorithms exhibit better robustness than the distributed affine projection algorithms in impulsive interference environments.

adaptive network;affine projection;sign algorithm;distributed estimation

2015-06-29;

2015-09-30；责任编辑：李勇锋

国家自然科学基金(No.61471251，No.61101217);江苏省自然科学基金(No.BK20131164)

TN911.72

A

0372-2112 (2016)07-1555-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.07.005