一类高阶整函数系数微分方程的复振荡

周　鉴,杨丛丽

(贵州师范大学 数学与计算机科学学院，贵州 贵阳　550001)



一类高阶整函数系数微分方程的复振荡

周鉴,杨丛丽

(贵州师范大学 数学与计算机科学学院，贵州 贵阳550001)

摘要：研究一类高阶整函数系数微分方程f(k)+A(z)f=0的解的增长级，得到当A(z)为超越整函数时，在一定条件下方程的任一非平凡解f的增长级不小于系数A(z)的增长级。

关键词：微分方程; 整函数; 增长级

0引言及已知的结果

对于某些复平面上的线性微分方程解的增长级的情况，国际数学人士S.Bank,I.Laine,G.Gunderson已经做了不少的研究，在国内高仕安，陈宗煊等人从事该领域的研究多年，已经有了许多有意义的结果，而关于于二阶方程f″+A(z)f=0的研究对进一步研究高阶方程具有指导意义，本文主要考虑形如：

f(k)+A(z)f=0

(1)

的线性微分方程，其中A(z)为超越整函数时方程解的增长级。

文章使用Nevanlinna值分布理论的相关记号，用m(r,f)、N(r,f)、T(r,f)、分别表示函数f的近似函数、极点密指量、特征函数。具体参见杨乐[1]或Hayman[2]等。

在文献[3]中S.Bank与I.Laine曾经证明了如下的定理

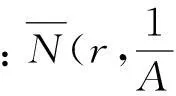
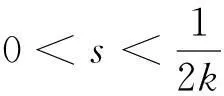
则对方程(1)的任一非平凡解f有 ρ(f)≥ρ(A)。

1所需引理

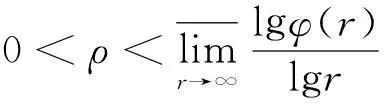
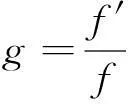
引理2.3[5]设f为超越亚纯函数，k≥2为整数，则

2定理2的证明

(2)

由ρ2<ρ(A)及引理2.1知，存在一个具有正上对密度的集合E0使得

T(r,A)≥rρ2r∈E0

(3)

取E=[r0,+∞)∩E0

结合(2)与(3)可得

(4)

由方程(1)有

(5)

及

(6)

(7)

利用定理已知条件及(7)有

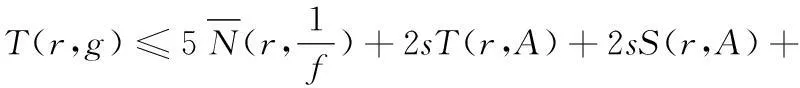
(8)

结合(4)，(6)，(8)又有

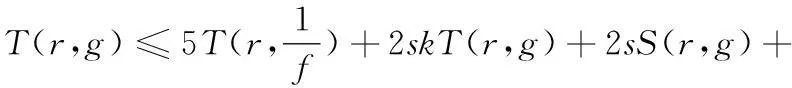
≤o(1)T(r,A)+2skT(r,g)+o(1)T(r,g)

≤o(1)T(r,g)+2skT(r,g)

=(o(1)+2sk)T(r,g)

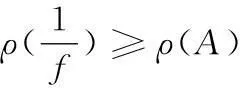
注如果以Θ(0,A)表示z=0对函数A(z)的亏量，其中A(z)零点不计重数，即

(9)

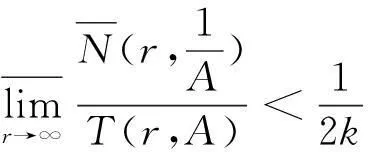
再利用定理2的结论ρ(f)≥ρ(A)可知 T(r,f)>S(r,A)。

最后我们得到推论

参考文献：

[1] 杨乐.值分布及其新研究[M].北京:科学出版社,1982.

[2] HAYMAN W.Meromorphic function[M].Oxford：Clarendon press,1964.

[3] BANK S,LAINE I .On the oscillation theory of f″+Af=0 where A is entire [J].Trans Amer Math，1982,73: 351-363.

[4] ISHIZAKI K,TOHGE K.On the complex Oscillation of some linear differentialequations [J].J Math Ana and Appl,1997,206:503-517.

[5] FRANK G,HENNEKEMPER W.Einige ergebnisse ber die werteverteilung memorpher Funktionen und ihrer ableitungen[J].Resultate Math,1981,4:39-54.

[6] BANK S,LAINE I.On the zeros of meromorphic solutions of second order linear differential equations[J].comment Math Helv,1983,58:656-677.

[7] 刘永,陈宗煊.一类高阶微分方程的复振荡[J].华南师范大学学报(自然科学版),2009,1(4):14-19.

[8] 蓝双婷,陈宗煊.高阶齐次线性微分方程解的零点[J].数学学报,2012,55(3):525-534.

[9] 曹廷彬,陈宗煊.一类高阶线性微分方程解的复振荡性质[J].数学杂志,2008,28(1):31-38.

文章编号：1004—5570(2016)01-0045-03

收稿日期：2015-10-20

基金项目：国家自然科学基金资助项目(11101099);贵州省科学技术基金(黔科合J字LKS[2009]04号)

作者简介：周鉴(1976-),男,硕士,副教授,研究方向:复分析,E-mail:zhoujiandepict@163.com.

中图分类号：O174.52

文献标识码：A

The complex oscillation of some kind of higher order diff-erential equations with entire function coefficients

ZHOU Jian,YANG Congli

(School of Mathematics and Computer science,Guizhou Normal University,Guizhou,Guiyang 550001,china)

Abstract:In this paper consider the order of growth of some kind of higher order linear differential equations f(k)+A(z)f=0 with entire function coefficients.It is shown that the order of growth of any non-trivial solutions of the equation not less than the order of growth of the coefficient A(z),if the A(z) is a transcendental entire function.

Key words:differential equations; entire function; order of growth