列车着火后继续在隧道中行驶的烟气特性*

郗艳红　毛军　白光　胡嘉伟

(北京交通大学 土木建筑工程学院∥轨道工程北京市重点实验室， 北京 100044)



列车着火后继续在隧道中行驶的烟气特性*

郗艳红毛军白光胡嘉伟

(北京交通大学 土木建筑工程学院∥轨道工程北京市重点实验室， 北京 100044)

保障隧道列车着火后继续向前行驶的安全性是火灾应急救援的目标.文中采用计算流体动力学方法，使用STAR-CCM+软件的滑移网格功能，研究了不同列车行驶速度和火源热释放速率对隧道内烟气特性的影响，得到列车携带火源在隧道内行驶时烟气温度的分布规律和最佳行驶速度.结果表明：隧道列车着火后继续向前行驶时,存在一个使温度达到最低的最佳行驶速度50km/h;当列车运行速度恒定时,火灾热释放速率越大,人眼高度处的最高温度也越高；热释放速率恒定时，最高温度随着列车行驶速度的增大先减小后增大，呈开口向上的抛物线形状;随着着火列车向前运行，列车车顶进风口的最高温度逐渐上升，在隧道横断面的中性面上，最高温度值有较大的振荡；在隧道内340m处温度最低，但是也达到了166.45 ℃.列车顶部区域的温度过高，可能会被烧毁性破坏，因此可考虑在列车着火后继续向前运动的同时给隧道通风，以降低环形空间的温度.

地铁隧道；列车火灾；烟气特性；数值模拟；热释放速率；温度

地铁隧道空间狭窄，热量易于积聚，列车在隧道内行驶发生火灾时，停在隧道内实施人员疏散和救援的难度很大.对于列车在区间隧道内着火的情况，德国、日本和我国地铁现行的安全措施均要求着火列车尽量驶到前方车站实施抢险救援[1],但是均未指出列车向前行驶的速度.

隧道列车着火后继续向前行驶时会形成迎风风流[2]，当此风流流过火源时，会带走火源处的热量，使燃烧强度减弱；同时，该风流也可能促使分子运动加剧，从而使燃烧强度增大.Carvd等[3]通过研究发现，隧道内发生火灾时，强制通风可能会抑制较小的火灾规模，也会使较大的火灾规模增强，因此在采用通风来控制烟气时，要使用合理的通风风速.

国内外学者对地铁火灾研究的较多[4- 11]，但是对隧道列车着火后继续向前行驶的安全性问题研究得较少[2,12- 13],且在这些相关研究中，均假定列车、火源和隧道处于静止状态，然而来流流向列车与列车携带火源在隧道内行驶的实际过程有一定差异.

因此，文中采用STAR-CCM+的滑移网格方法，对隧道内列车着火后继续向前行驶进行数值模拟计算，分析着火列车周围烟气场的分布特性，为进一步研究有关的运动体火灾特性提供参考.

1　缩尺模型实验的数值模拟

笔者所在课题组进行了隧道列车运动火源模型实验，得到了一系列实验数据[14].该模型是以北京某地铁车站的区间隧道作为原型，火灾模型实验台的几何比例尺为1∶8.为了验证数值模拟方法的正确性，以燃料加注量68.31g、小车速度0.296m/s为例，对模型实验进行数值模拟计算.

严格按照模型实验中的尺寸建模，数值模拟中设置的隧道顶面的热电偶分布与模型实验相同，示意图如图1所示.

图1　隧道顶面热电偶分布(单位：mm )

Fig.1Thermocoupledistributionatthetopofthetunnel(Unit：mm)

1.1数值条件设定

(1)初始条件.隧道内各处压力均为一个大气压；隧道长度、宽度和高度方向的速度均为0m/s；环境温度为20 ℃.

(2)壁面条件.隧道进出口均设置为压力出口边界，相对大气压强为0Pa；隧道壁面和地铁列车壁面均为无滑移边界条件，壁面粗糙度为0.013mm，辐射系数为0.85.

1.2计算结果与实验结果的对比

由于篇幅有限，仅给出4个测点的温度对比图，如图2所示.由图可知：小车携带火源向前运动时，实验中的温度值围绕初始值上下波动；当火源经过测点时，温度达到最大值；当火源离开时，温度缓慢下降.而对于数值模拟结果，当火源到达测点之前，数值模拟的温度值均为室温；当火源到达瞬间，温度快速上升；火源离开之后温度缓慢下降.用这两种方法得到的温度的最大值仅相差5%，因此，可以认为数值模拟方法是适用的.

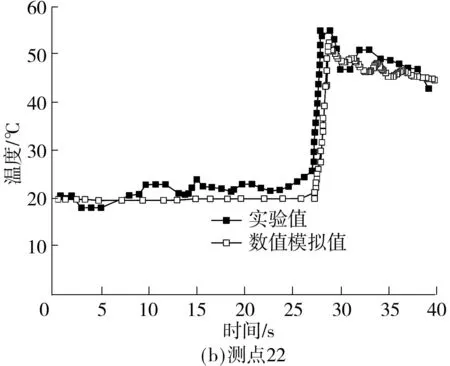
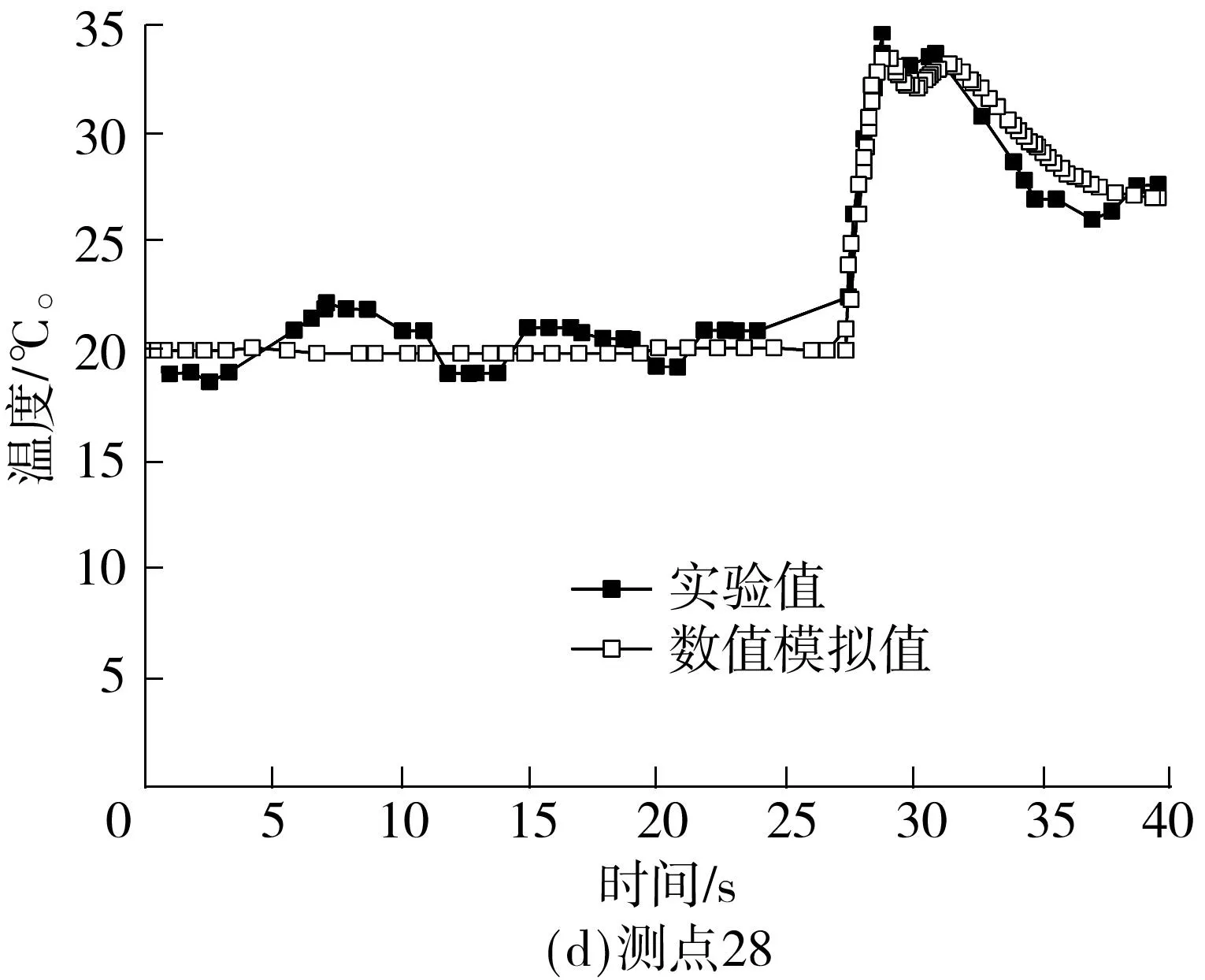
图2　数值模拟与实验结果的对比

Fig.2Comparisonofexperimentalandnumerically-simulatedresults

2　地铁列车运动火灾数值模拟

2.1计算模型及边界条件

取北京某地铁车站的区间隧道为计算对象进行分析.隧道断面长×宽×高为1 290m×4.25m×5m，两车站长×宽×高为150m×20m×6.7m；地铁列车单辆车厢长×宽×高为20m×3m×3.5m，一共6辆编组，总长120m.火源位于列车中部；采用笛卡尔坐标系，x、y、z分别代表隧道的宽度、长度和高度方向，列车沿y方向运行,隧道模型示意图如图3所示.

图3　隧道模型示意图(单位:m)

在列车附近沿隧道纵向每隔50m布置1个测点，沿隧道高度方向布置14个测点.沿隧道宽度方向测点主要布置在列车顶面与隧道顶壁之间、列车侧面与隧道侧壁之间的空间内，其中x=0.312 5m为隧道与列车环形空间的中心线，x=2.125 0m为列车隧道(列车)中心线，如图3(b)所示.

列车运行时间由列车的运行速度决定，计算时间步长为0.001s.采用trim网格，网格量为650万.采用滑移网格技术来模拟列车的运动过程[15]，列车及其周围的网格按照规定方向和速度移动.在隧道围护结构和列车表面上，速度分量均采用无滑移边界条件.隧道及列车壁面均采用钢质材料，粗糙度均取为0.013mm，辐射系数设为0.85.

2.2数值模拟的火灾工况

共模拟30个工况，列于表1中，所有工况均假定产生的烟气全部在隧道中蔓延，而忽略进入到列车中的情况，故也不考虑列车内部的通风模式.列车到达的相对位置如图4所示,列车到达相应位置所需时间如表2所示.

表1　模拟工况

1)HRR为火源热释放速率.

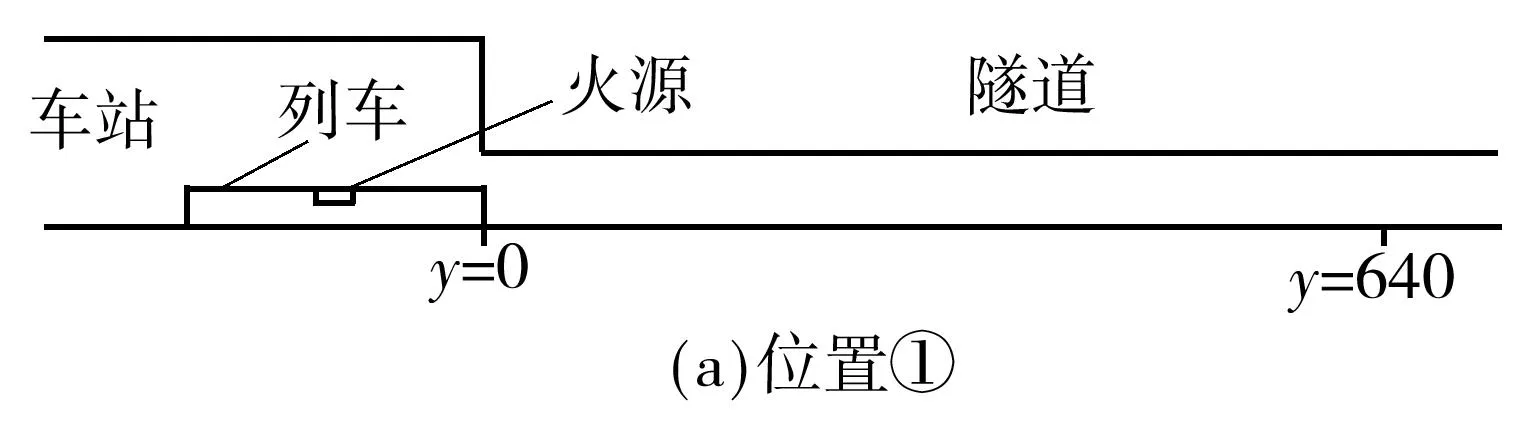
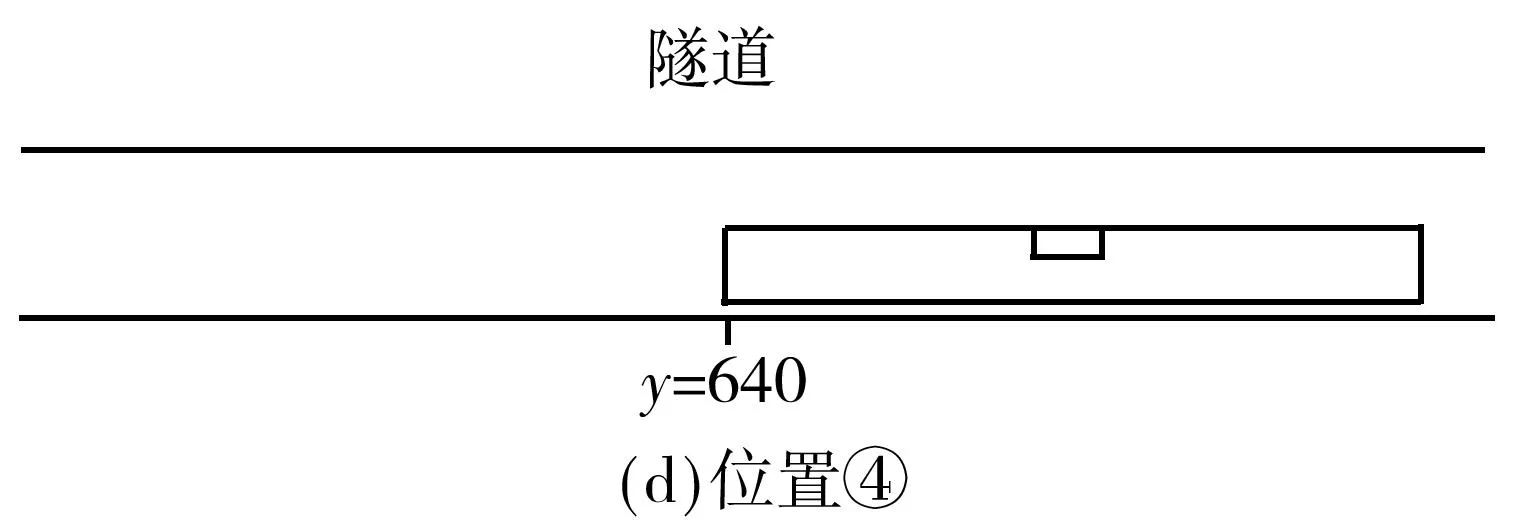
图4　列车到达的相对位置(单位：m)

运行速度/(km·h-1)运行到图4相应位置时所需时间/s位置①位置②位置③位置④200115.20126.00136.8030076.8084.0091.2040057.6063.0068.4050046.0850.4054.7260038.4042.0045.60

3　结果分析

通过数值模拟结果，分析不同火源释放速率下着火列车在隧道内行驶的速度对温度的影响，进而确定列车在隧道中发生火灾时的最合理运行速度.

3.1车速对列车-隧道环形空间烟气分布的影响

3.1.1车顶与隧道环形空间

以隧道宽度中心线x=2.125 0m、隧道长度y=640m及隧道高度z=4.324m为典型位置，分析此处的温度随车速变化的规律.

图5为同一热释放速率、不同车速时的测点温度图.由图可知，列车着火后继续在隧道内行驶时，在同一热释放速率下，列车的行驶速度对列车火灾的火势具有决定性的影响，测点的最高温度值均在列车速度为50km/h时取得最小值，且各个热释放速率下的温度值都小于60 ℃，故此速度可以看成是着火列车在隧道中行驶的最佳速度.列车速度在20～50km/h范围内，随着车速的增大，通过火源的迎风风流带走的热量也增多，即由导热、对流和辐射带走的热量大于由可燃物和氧分子接触面及接触几率增大产生的释热量增量，测点温度值随列车速度的增大而减小.随着迎风风流速度继续增大，即列车运行速度增大到60km/h时，燃烧由燃料控制转变为通风控制，释热量增量大于由导热、对流和辐射带走的热量，同一热释放速率下，测点的温度值上升.

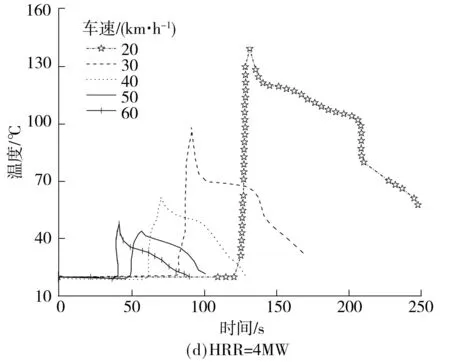
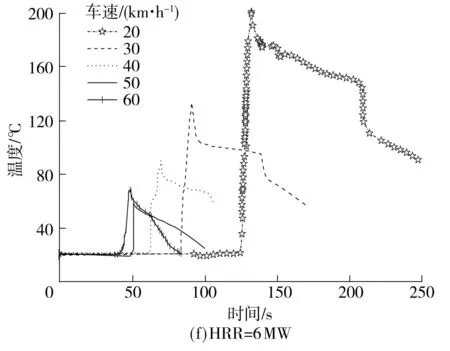
图5同一热释放速率下不同车速时的测点温度图

Fig.5Temperaturesofthemeasuringpointsatthesameheatreleaseratebutdifferenttrainspeeds

3.1.2人眼高度处烟气最高温度随列车速度变化的规律

人眼高度处温度对人的生命安全极其重要，图6反映了人眼高度位置(z=1.500m)的温度随热释放速率和列车速度变化的规律.由图可知，在同一热释放速率下，最高温度值均在列车速度为50km/h时取得最小值，与车顶位置高度的温度变化情况相同.另外，即使在火灾热释放速率达到6MW、列车以不同速度行驶时,人眼高度处的温度也均不超过75 ℃，下游车厢乘客是安全的.下面对人眼处的最大温度随热释放速率和列车运行速度的变化规律进行分析，最大温度值如表3所示.

表3　z=1.500 m处的最大温度

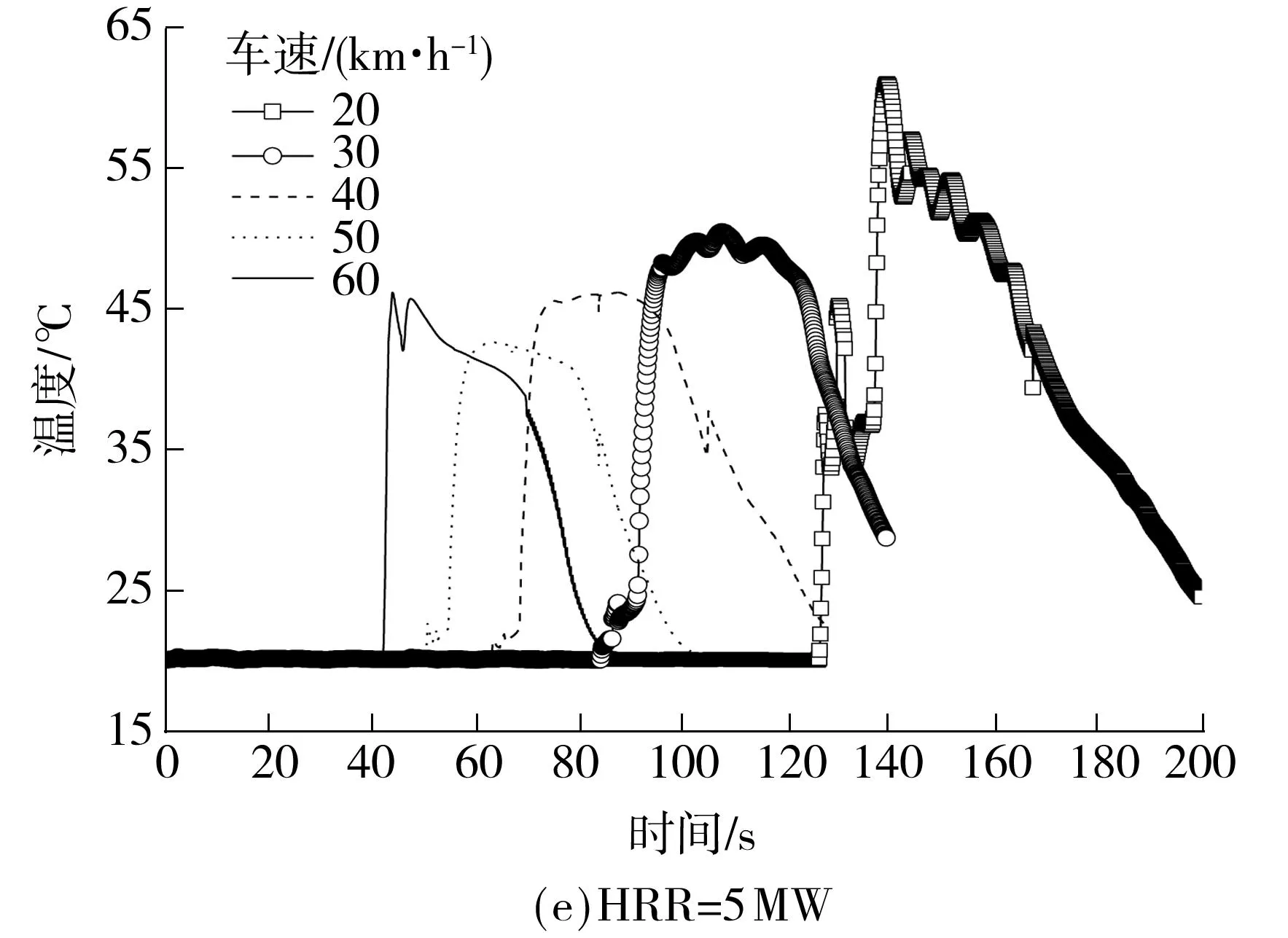
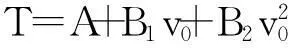
图 7　z=1.500 m处最大温度的拟合曲线

Fig.7Fittingcurvesofthemaximumtemperatureattheheightofz=1.500m

表4z=1.500m处最大温度拟合曲线的系数

Table4Fittingcurvecoefficientsofthemaximumtemperatureattheheightofz=1.500m

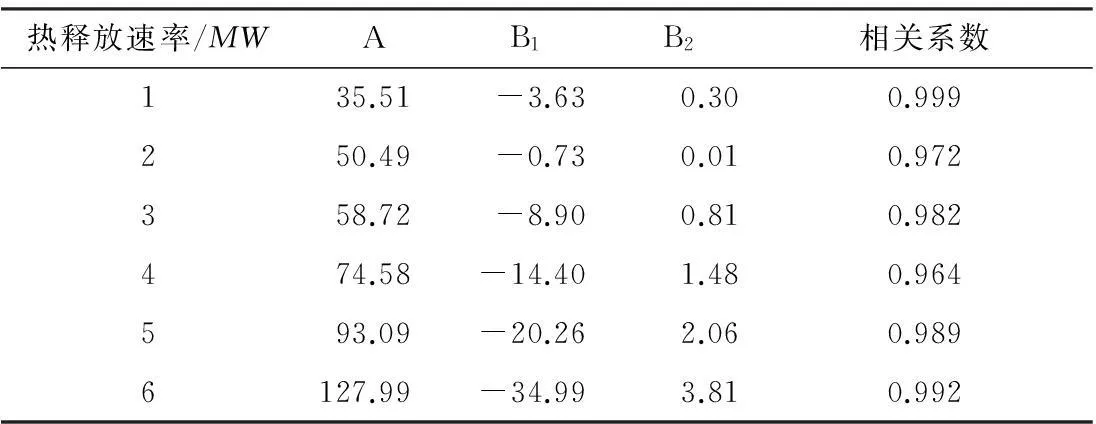
热释放速率/MWAB1B2相关系数135.51-3.630.300.999250.49-0.730.010.972358.72-8.900.810.982474.58-14.401.480.964593.09-20.262.060.9896127.99-34.993.810.992

由图7可知：列车运行速度恒定时，火灾热释放速率越大，人眼高度处的最高温度也越大；热释放速率恒定时，最高温度随着列车行驶速度的增大先减小后增大，呈开口向上的抛物线形状，当列车速度为50km/h时，达到温度的最小值.

3.2典型火灾工况分析

由3.1节可知，不同热释放速率下，列车速度为50km/h时温度最低.因此，以火源热释放速率为5MW、列车着火后以50km/h向前行驶为典型工况，以隧道长度中心y=640m为典型位置，分析近列车车顶进风口的高度z=3.890m处的温度变化情况，隧道沿纵向各测点的温度随时间的变化曲线如图8所示.

图8　沿隧道纵向温度的变化曲线(x=0.312 5 m)

Fig.8Changingcurvesoftemperatureindifferentlocationsalongthetunnel(x=0.312 5m)

由图8可知，沿隧道纵向(列车运行方向)最高温度逐渐上升，即着火列车向前运行时，列车车顶进风口的最高温度是逐渐上升的，且与离开隧道的距离成二次曲线关系.最高温度及其拟合曲线分别如表5和图9所示.由表5可得拟合曲线为T=38.53+0.17y-0.000 013y2.

在列车顶部与隧道环形空间里(x=2.125 0m)，z=3.890m处依然是最高温度所在的高度.为了分析列车顶部的受害潜在危险性，仍然取z=3.890m高度处的测点进行分析.图10给出了x=2.125 0m断面处、z=3.890m的高度位置隧道纵向各个测点的温度变化规律.由图可知,各个点的温度均随着着火列车的运行先增到最大值,之后逐渐减小为一个常数.

图11给出了沿隧道纵向各测点的最高温度.由图可知，在x=2.125 0m的断面上，最高温度有较大的振荡，在y=340m处温度最低，但是也达到了166.45 ℃.列车顶部区域因温度过高可能会被烧毁性破坏.因此，可考虑在列车着火后继续向前运动的同时给隧道通风，以降低环形空间的温度，具体的隧道通风模式是笔者正在研究的课题.

表5　沿隧道纵向测点的最高温度

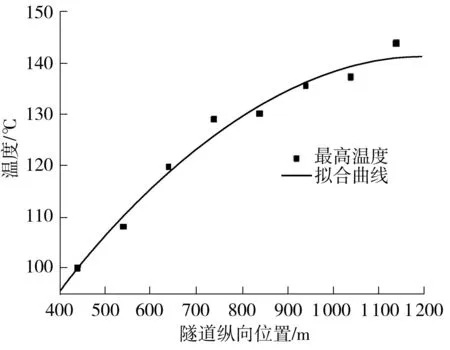
图9　沿隧道纵向测点的最高温度拟合曲线

Fig.9Fittingcurveofthemaximumtemperatureofthemeasu-ringpointsindifferentlocationsalongthetunnel

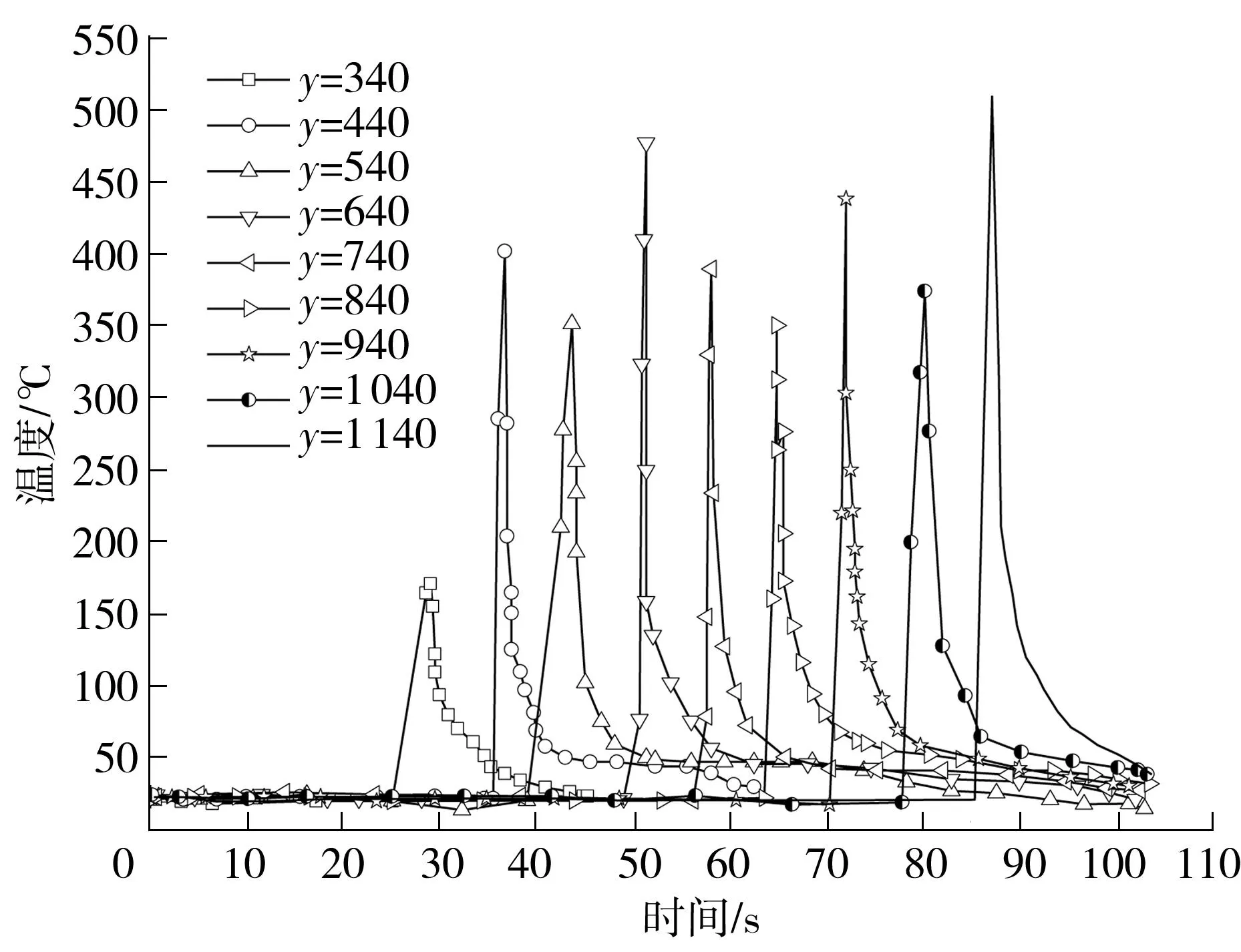
图10　沿隧道纵向温度的变化曲线(x=2.125 0 m)

Fig.10Changingcurvesoftemperatureindifferentlocationsalongthetunnel(x=2.125 0m)

图11　沿隧道纵向测点的最高温度(x=2.125 0 m)

Fig.11Maximumtemperaturesofthemeasuringpointsindiffe-rentlocationsalongthetunnel(x=2.125 0m)

4　结论

(1)隧道列车着火后继续向前行驶时形成迎风风流，此迎风风流有可能使火灾强度增强或减弱，因此，存在一个最佳列车行驶速度，其产生的迎风风流流动速度使火灾燃烧强度达到最小，即令温度达到最低.

(2)相同的热释放速率下，列车以20～50km/h的速度向前行驶时，随着车速的增大，温度随列车速度的增大而降低；当列车运行速度增大到60km/h时，测点温度上升.即在各个热释放速率下，测点温度均在车速为50km/h时取得最小值，此车速为隧道列车着火后继续向前行驶的安全速度；

(3)列车运行速度恒定时，火灾热释放速率越大，人眼高度处的最高温度也越大；热释放速率恒定时，最高温度随着列车行驶速度的增大先降低后升高，呈开口向上的抛物线形状；当列车速度为50km/h时，达到温度的最小值；

(4)随着着火列车的向前运行，近列车车顶进风口高度处的温度有较大的振荡，最低温度为166.45 ℃.可考虑在列车着火后继续向前运动的同时给隧道通风，以降低环形空间的温度，防范烧毁性破坏.

[1]王铭珍．国外地铁如何防火 [J]．山东消防，2003(4)：9- 10.

WANGMing-zhen.Howtopreventfiresinabroad[J].ShandongFire,2003(4)：9- 10.

[2]郗艳红，毛军，樊洪明,等．地铁列车着火后在隧道内行驶的安全速度的实验研究 [J]．华南理工大学学报(自然科学版)，2010，38(3)：25- 30，36.

XIYan-hong,MAOJun,FANHong-ming,etal.Safetyvelocityofon-firetrainmovinginsubwaytunnel[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition)，2010，38(3)：25- 30，36.

[3]CARVDRO,BEARDAN,JOWITTPW.Theinfluenceoftunnelgeometryandventilationontheheatreleaserateoffire[J].FireTechnology,2004,40(1):5- 26.

[4]LIYZ,FANCG,INGASONH.Effectofcrosssectionandventilationonheatreleaseratesintunnelfires[J].TunnellingandUndergroundSpaceTechnology,2016,51:414- 423.

[5]CHOWWK,GAOY,ZHAOJH.Astudyontiltedtunnelfireundernaturalventilation[J].FireSafetyJournal,2016,81:44- 57.

[6]LIYan-feng,BIANJiang,LIJun-mei.Researchonsmokeflowinatunnelfireofsubwaysystem[J].OriginalResearchArticleProcediaEngineering,2014，71:390- 396.

[7]HARISHR,VENKATASUBBAIAHK.Effectsofbuoyancyinducedroofventilationsystemsforsmokeremovalintunnelfires[J].TunnellingandUndergroundSpaceTechnology，2014，42:195- 205.

[8]JAESeongRoh,HONGSunRyou,WONHeePark,etal.CFDsimulationandassessemntoflifesafetyinasubwaytrainfire[J].TunnellingandUndergroundSpaceTechnology,2009，24(4):447- 453.

[9]MENGNa,HULonghua,WULong,etal.Numericalstudyontheoptimizationofsmokeventilationmodeattheconjunctionareabetweentunneltrackandplatforminemergencyofatrainfireatsubwaystation[J].TunnellingandUndergroundSpaceTechnology,2014，40:151- 159.

[10]JIJ,ZHONGW,LIKY,etal.Asimplifiedcalculationmethodonmaximumsmoketemperatureundertheceilinginsubwaystationfires[J].TunnellingandUndergroundSpaceTechnology,2011,26(3):490- 496.

[11]AHMEDKashef,YUANZhongyuan,LEIBo.Ceilingtemperaturedistributionandsmokediffusionintunnelfireswithnaturalventilation[J].FireSafetyJournal,2013，62:249- 255.

[12]WANGCHC,WARGOJD.Experimentalstudyofthermallygeneratedreversestratifiedlayersinafiretunnel[J].CombustFlame,1986,66:171- 180.

[13]徐志胜，周庆，徐彧．运行旅客列车隧道火灾模型实验及数值模拟 [J].铁道学报，2004，26(1)：124- 128.

XUZhi-sheng,ZHOUQing,XUYu.Firemodelexperimentandnumericalsimulationofpassengertrainsrunningintunnels[J].JournaloftheChinaRailwaySociety,2004，26(1)：124- 128.

[14]郗艳红.轨道交通典型火灾的动力学特性研究 [D].北京:北京交通大学土木建筑工程学院，2014.

[15]戚振宕.高速列车明线会车气动特性研究 [D].成都:西南交通大学车辆工程专业，2010.

Foundationitems:SupportedbytheJointFoundationforBasicResearchofHighSpeedRailway(U13342023)

CharacteristicsofSmokeinTunnelwithOn-FireTrainMovinginSubwayTunnel

XI Yan-hongMAO JunBAI GuangHU Jia-wei

(SchoolofCivilEngineeringandArchitecture∥BeijingKeyLaboratoryofTrackEngineering,BeijingJiaotongUniversity,Beijing100044,China)

Ensuringthesafetyoftheon-firetrainmovinginasubwaytunnelisthegoalofthecorrespondingemergencyrescue.Inthispaper,withthehelpofSTAR-CCM+possessingthefunctionofmeshsliding,CFD(ComputationalFluidDynamics)simulationsarecarriedouttoinvestigatetheeffectsoftrainspeedandheatreleaserateonthesmokecharacteristicsinatunnel,andthedistributionofsmoketemperatureaswellastheoptimalspeedoftheon-firetraintravelinginthetunnelareexplored.Theresultsshowthat(1)fortheon-firetrainmovinginasubwaytunnel,thereisanoptimalspeedcorrespondingtothelowesttemperature,namely50km/h;(2)whenthetrainmovesataconstantspeed,thetemperaturepeakatthetypicaleyepointsincreaseswiththeheatreleaserate;(3)ataconstantheatreleaserate,themaximumtemperaturefirstdecreasesandthenincreaseswiththetrainspeed,presentinganupwardparabola;(4)thetemperatureatthetrainroofinletgraduallyincreaseswhentheon-firetrainmovesforwardinthetunnel,andthemaximumtemperatureisofalargeoscillationontheneutralsurface;(5)theminimumtemperature(166.45 ℃)occursat340minthetunnel;and(6)thetrainmightbeburntduetothehightemperatureatthetraintop,sothataventilationmeasureshouldbeadoptedtoreducethetemperatureoftheannulartunnelspacewhenasubwaytrainisonfire.

subwaytunnel;trainfire;smokecharacteristic;numericalsimulation;heatreleaserate;temperature

郗艳红(1980-)，女，博士后，讲师，主要从事火灾安全、高速列车空气动力学与行车安全等的研究.E-mail:yhxi@bjtu.edu.cn

1000- 565X(2016)06- 0129- 08

U231;TU89

10.3969/j.issn.1000-565X.2016.06.020

2015- 05- 15

高速铁路基础研究联合基金资助项目(U13342023)；中国铁路总公司科技研究开发计划课题(2015G001-G)