水下爆炸气泡与浮体结构相互作用的研究
2016-08-04王加夏姜明佐
王加夏 , 宗 智 ,2, 周 力 , 姜明佐
(1.大连理工大学 船舶工程学院,辽宁 大连 116024;2. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024;3. 大连理工大学 控制科学与工程学院,辽宁 大连 116024)
水下爆炸气泡与浮体结构相互作用的研究
王加夏1, 宗智1,2, 周力1, 姜明佐3
(1.大连理工大学 船舶工程学院,辽宁 大连116024;2. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连116024;3. 大连理工大学 控制科学与工程学院,辽宁 大连116024)
基于势流理论,利用三维边界积分法模拟水下爆炸气泡与其附近浮体之间的相互作用,同时考虑到自由液面对气泡特性的影响。该数值计算结果与电火花气泡实验结果吻合良好,验证了该数值方法的有效性;通过爆点与自由液面的距离,爆点与结构的距离,结构的运动响应三个方面来研究近自由面时,气泡、浮体结构和自由液面之间的耦合特征。尤其关注它们对气泡动力特性,结构上的压力载荷以及自由液面升高等方面的影响。
水下爆炸气泡;边界积分法;浮体结构;刚体运动
水下爆炸气泡的研究在军事和工程中具有广泛的应用,比如气泡造成附近结构物的破坏和损伤。当气泡在不同边界演化时,会表现出不同的动力学特性,导致了该问题的复杂性,同时也使得该问题成为研究的热点领域。当气泡靠近自由液面时[1-3],气泡在自由液面和浮力共同作用下,气泡射流的形态,液面的升高等是研究的重点。当气泡靠近固定结构物时[4-7],气泡的形状,气泡载荷作用于结构上的压力等为关注的对象。当气泡靠近运动或复杂结构[8-13]时,气泡与结构的相互耦合等是这方面研究的热点。然而,在实际问题中,这些边界并不是单一存在,比如当爆炸气泡与水面舰船的相互作用耦合时,就需要同时考虑结构、液面和浮力的联合作用。这样就增加了气泡问题研究的多样性和复杂性。目前关于爆炸气泡与其附近浮体结构相互作用的研究较少,其中Klaseboer等[14]在爆点距离液面较远时,利用镜像法计入自由液面效应并计算了气泡与水面舰船的相互作用。但该方法适用于自由液面近似平坦时,当爆点距离较近时,液面的抬升现象明显,该方法就不再适用。在以往计算气泡与自由液面相互作用时,主要研究爆点与液面距离对液面升高的影响,较少考虑到浮体结构的影响。并且,之前文献在研究气泡与结构物相互作用载荷时,主要关注爆点与结构物距离对载荷的影响,较少研究爆点与自由液面的距离对气泡载荷的影响。本文采用三维边界积分法,通过直接在自由液面划分网格的方式计入了自由液面的影响,同时能观察液面形态的变化,数值模拟了考虑自由面与浮体结构附近水下爆炸气泡的运动特征。通过研究爆点与自由液面的距离,爆点与浮体的距离,以及两种不同的结构运动特征,揭示了近自由面时,气泡、结构和自由液面三者之间相互耦合的特征。
1计算模型
在研究水下爆炸气泡阶段时,通常将流体域Ω当成无黏,无旋,不可压缩[15]的理想流体,即控制方程满足Laplace方程
2φ=0
(1)
根据Green 第二定理,控制方程可以写成如下形式
c(P)φ(P)
(2)
式中:P=(x,y,z)是场点,Q=(x′,y′,z′)是源点。c(P)=∫S∂G/∂ndS[16]为从P点观察到的立体角,n为指向流体域外的法向方向,G(P,Q)=1/|Q-P|=1/rPQ为自由空间的格林函数,rPQ=[(XQ-XP)2+(YQ-YP)2+(ZQ-ZP)2]1/2为场点和源点的距离,∂/∂n=n·为边界S上的法向倒数,其中S包括气泡边界Sb,结构边界St和自由液面边界Sf。计算坐标系见图1,其中包含本文重点研究的两个无量纲参量:爆点与自由面的距离γf,爆点与浮体结构的距离γs。

图1 爆炸气泡与漂浮结构相互作用的坐标系和几何图Fig.1 The coordinate system and geometry used to simulate the interaction between the bubble and floating structure
对气泡和自由液面的运动学边界条件为:

(3)
对于结构需要满足不可穿透条件:
(4)
动力学边界条件为:
(5)
式中:P∞=Patm+ρgH为爆点的静水压力,H为爆点的深度。Patm为标准大气压,ρ为流体的密度。对于自由液面P=Patm,对于气泡,压力P包括两部分,饱和蒸汽压Pc和满足多方定律的不可凝结气压,即P=Pc+Pg0(V0/V)λ,其中Pg0和V0是气泡初始的压强和体积,λ是热比率,对于TNT炸药λ=1.25[17]。
对于水下爆炸气泡,初始压强可通过下式计算:
(6)
式中:W为药量;ΔP=P∞-Pc;Rm=3.38×(W/(H+10))1/3是最大气泡半径;V0=4πR03/3,其中R0为初始气泡半径,可以通过Rayleigh-Plesset方程求解[14]:
(7)


(8)
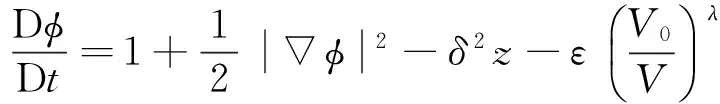
(9)
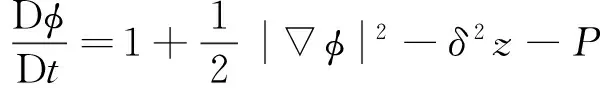
(10)
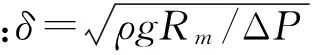
2数值求解
对爆炸气泡与附近浮体的相互作用的数值模拟,首先将边界S划分成三角形网格,这样单元表面上的位置和速度势可由形函数和节点坐标来表示,即
(11)

(12)
式中:N1=ξ;N2=η;N3=1-ξ-η。为了计算三角形单元的积分,需要将整体坐标系的单元转变为局部的二维坐标系,此时的面积积分为:
(13)
式中J为转变过程中生成的雅克比值。利用式(11),式(12)和式(13),经过离散后的式(2)变为:


(14)
式中:M为边界离散的单元数,为了简化,可将式(14) 写成如下形式:


(15)
式中:
(16)
(17)
式(15)可以写成如下的矩阵形式:

(18)
式中:N为离散边界的总单元数。对于系数矩阵H和G的非对角元素可以采用7点高斯积分公式计算[18]。系数矩阵H和G的对角元素出现奇异性,由于G对角元素为弱奇异,可以通过极坐标变换的方式消除奇异性[18]。对于H的对角元素出现强奇异,针对封闭区域比如气泡,可通过4π法则求解[19]即
(19)
对于自由面或者漂浮的结构,需要通过立体角的定义直接进行求解,即线性单元在以该点为中心的单位球面上投影面积,具体可参考文献[20-21]。
在计算过程中,由于网格的大变形易导致数值计算的不稳定性,需要引入光顺算法[22]和弹性网格技术(Elastic Mesh Technique,EMT)[23]。同时为了控制边界速度势的改变量也为了保持计算的稳定性,采用变时间步长的方式,即:
(20)
(21)
Δt=min{Δt1,Δt2}
(22)
式中:Δφ取常数0.02。
3刚体运动
气泡的动力学特性与结构的动态响应是相互作用,相互影响的。结构响应会对气泡的脉动周期,作用于结构上的气泡载荷等产生影响。因此为了准确模拟水下爆炸的气泡对附近结构物的影响,需要采用耦合算法。本文主要考虑在爆炸气泡载荷作用下物体做自由平动和转动的刚体运动时的情况。此时需要引入两个坐标系,一个是物固坐标系xyz,另一个是空间坐标系XYZ。计算模型和坐标系见图2。

图2 刚体运动中两个坐标系的定义Fig.2 The definition of two coordinate systems in rigid body motion
根据经典力学理论[24],六自由度的刚体运动的动量和角动量方程为:
(23)
(24)
其中矩阵[m]=diag(m,m,m)和 [I]=diag(Ix,Iy,Iz)分别为质量和转动惯量矩阵,[u]=[ux,uy,uz]T和 [ω]=[ωx,ωy,ωz]T分别为物固坐标系下的平动和转动速度。[Fr]=[Fx,Fy,Fz] 和 [Mr]=[Mx,My,Mz]为作用在刚体上的力和力矩。
其中力和力矩可以表示为:
Fr=∫SwP·nxyzdS
(25)
Mr=∫SwP·(rxyz×nxyz)dS
(26)
式中:rxyz和nxyz分别为刚体的位置和法向向量,Sw为结构湿表面。
由于计算漂浮结构的刚体运动,首先通过式(3)计算得自由面与结构连接点的位置,然后对该连接点以下的结构上的节点进行重新均匀分布,最后通过插值获得新节点的相关参数的值。
4计算模型的验证
通过数值计算结果与Chahine等[25]的气泡与浮体结构相互作用的电火花实验进行对比,验证本文数值方法的有效性。实验中浮体结构分别为固定不动和刚体运动的垂直圆柱,圆柱的尺寸和实验参数可见文献[25]。图3给出了固定不动垂直圆柱的实验和数值计算结果。此时γf=1.95,γs=0.91即0.91倍的最大气泡半径。当气泡膨胀至最大体积之前,气泡已经靠近结构,此时气泡会在结构附近继续膨胀,使得气泡顶部出现明显的扁平状,在气泡溃灭时,由于溃灭气泡和边界之间的低压区[26],会使得气泡形成长条状,在结构物的Bjerknes吸力和气泡浮力的共同作用下,气泡底部出现向上的射流。图4给出了气泡上下节点的运动轨迹。从图4可知,气泡在膨胀到最大体积后,气泡顶部节点一直贴近结构物底部,底部节点在溃灭时向上射流的作用下,大幅度向上移动。从图3和图4的对比可知,数值模拟的气泡形状以及上下节点的运动轨迹均和实验吻合良好。说明了边界积分法能够准确模拟气泡与固定漂浮结构的相互作用。

图3 固定垂直圆柱的气泡形态的数值与实验对比Fig.3 The experimental and numerical bubble shapes for an explosion beneath a fixed vertical cylinder

图4 气泡上下顶点轨迹的数值与实验结果对比Fig.4 Comparison of numerical and experimental results of position history of top and bottom points for an explosion beneath a fixed vertical cylinder
在实际中,由于结构响应与气泡运动特征是相互耦合的过程,为了准确模拟实际情况,还需要把结构的响应考虑进来。下面主要模拟电火花气泡与刚体运动结构的相互作用,算例中γf=2.25,γs=1.19。图5给出了气泡与刚体垂直圆柱的高速摄影和数值模拟结果。从图中可以看出,在气泡最大体积时,对于刚体运动的圆柱,气泡顶部扁平现象明显减弱,同时气泡与结构物之间的距离明显增大。随后气泡开始收缩,气泡出现“梨”状,最后近一步收缩成“水滴状”。通过图3与图5的对比,能清楚看到结构的运动形式对气泡形态和脉动周期的影响。

图5 刚体运动垂直圆柱的实验和数值形态对比Fig.5 The experimental and numerical bubble shapes for an explosion beneath a movable vertical cylinder
图6和图7分别给出了气泡的上下顶点以及圆柱的重心的数值与实验对比结果。从以上对比可知,数值模拟与实验结果大致吻合。从图7可知,计算重心的位移较实验中偏小,这可能是由于忽略流场黏性以及实验中结构底部形成的小气泡有关。通过上述对比,可以看到三维边界积分法能够较为准确的模拟气泡与不同运动特征的漂浮结构的相互作用。

图6 气泡上下顶点轨迹的数值与实验对比Fig.6 Comparison of numerical and experimental results of position history of top and bottom points

图7 结构物重心轨迹的数值与实验对比Fig.7 Comparison of numerical and experimental results of position history of center of gravity
5算例
本文通过研究爆点与自由液面的距离γf,爆点与结构的距离γs以及结构的运动形式这三个方面来更好的认识水下爆炸气泡与其附近浮体结构的相互作用。计算中气泡离散成642个节点和1 280个三角形单元,方箱被离散成741个节点和1 400个三角形单元,液面被离散为1 600个节点和3 040个三角形单元。在本节算例中,均采用同一结构,结构的无量纲尺寸分别为长度为5.4,宽度1.8,高度2,厚度为0.026 3,方箱的密度为7 800 kg/m3。计算中网格划分可见图8。
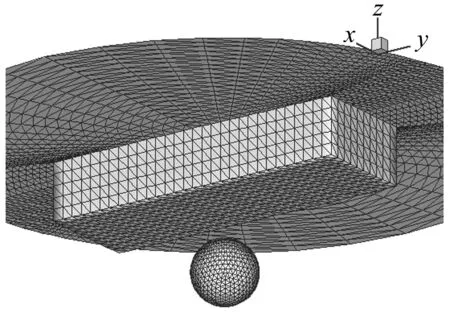
图8 计算的网格划分情况Fig.8 The triangulation mesh utilized in simulation of bubble beneath floating structure
5.1固定γf=1.8时,不同γs的影响
图9给出了近自由面(γf=1.8)时,爆点与浮体底部之间的距离参数γs分别在1.1,1.2,1.3,1.4情况下,爆炸气泡与其附近浮体之间的相互作用的演化过程。气泡参数取值为:药量为59.2 kg, 深度H=8.9 m,Rm=4.94 m,ε=379.8,δ=0.5,R0=0.092 4。图9中云图表示作用在结构上的无量纲压力。当气泡靠近不同边界时,气泡的射流和迁移方向可近似由γδ=0.442[4]近似判定,在算例中,γfδ和γsδ均>0.442,因此在计算中出现向上方向的射流。从γf=1.8,γs=1.1的气泡和附近浮体结构的演化过程可看出,在膨胀阶段(t=0.107 3),气泡保持着球状,此时液面出现了小幅的升高。气泡在t=0.963 9时,体积达到最大,并且在结构物的作用下,气泡顶端出现了扁平状, 此时液面抬升显著。随后,气泡开始收缩,液面的高度随之下降,同时在结构物,液面和浮力的共同作用下,气泡底端形成了向上的射流。在t=2.011 3时,气泡体积收缩至最小值,液面的高度降至最低,并且在结构物底部出现了明显的高压区。
通过第二行气泡体积最大时的对比可知,随着γs的增大,气泡越来越呈现出球形,气泡顶端的扁平状消失,同时液面的高度增大。当气泡靠近结构膨胀时,气泡向结构运动,这是由于结构和气泡之间的低压区造成的。当γs越小,结构对气泡的吸引越大,此时流场中低压区越小,使得液面的抬升也就越小。通过第四行气泡体积最小时的对比可知,随着γs的增大,气泡的第一次脉动周期越小,这主要因为γs越大,气泡在溃灭时,就更能够保持对称状态,在射流穿透气泡时,气泡的体积越小(见图12),因此气泡脉动周期越小。
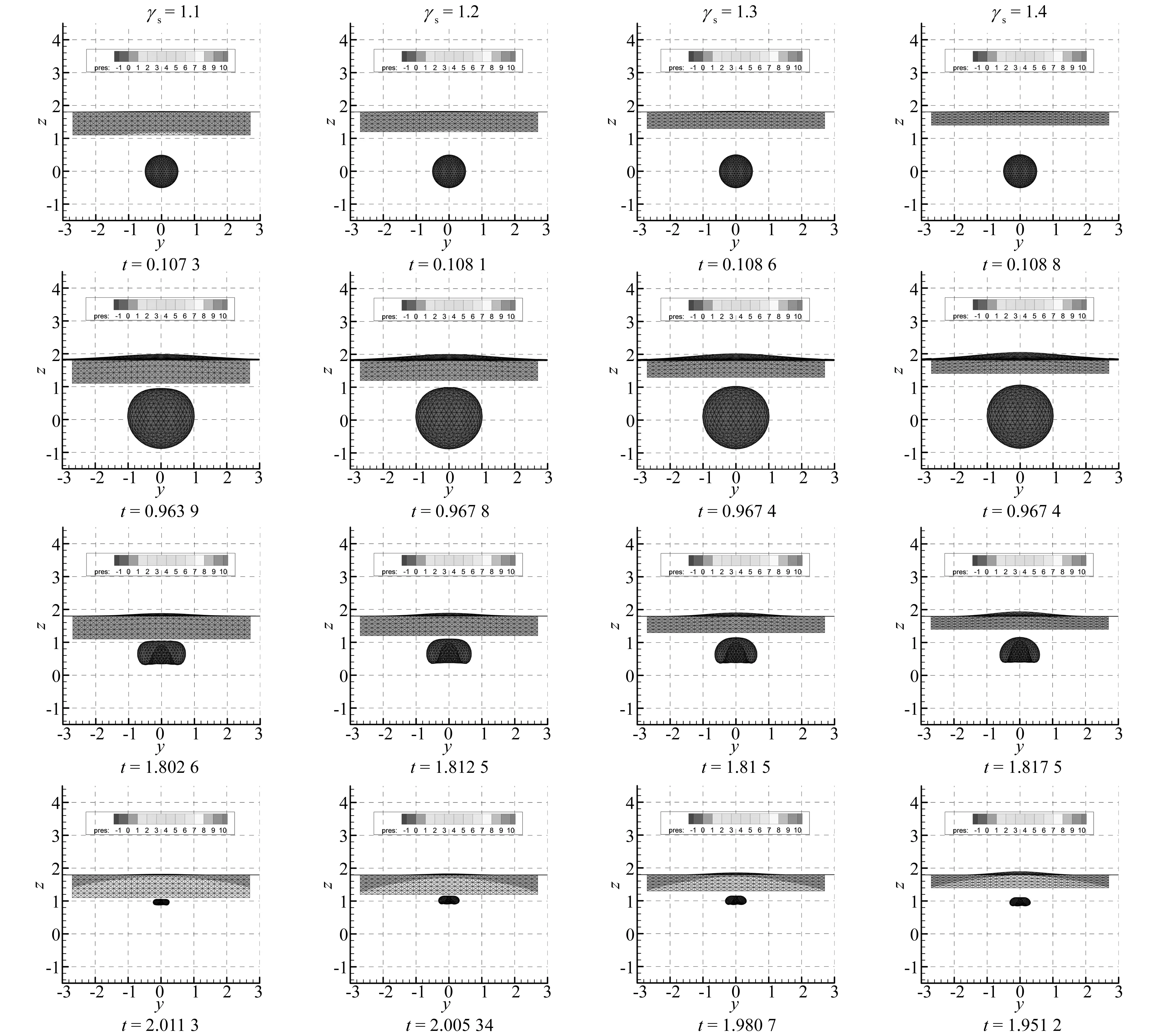
图9 γf =1.8时不同γs下,爆炸气泡与附近浮体结构的演化过程Fig.9 The evolution of bubble near floating structure at different γs when γf =1.8
图10和图11给出了结构底部中心点的压力和结构中部与液面交接点处液面高度的时间历程曲线。从图10可知,在初始时刻高温高压爆炸气团的作用下,在结构物底部中心点处出现一个高压,随着气泡的膨胀,中心点处压力急剧减小,当气泡收缩至最小体积时,在中心点处出现气泡载荷的压力峰值。随着γs的增大,结构物离爆点增大,使得作用在结构中心点处的气泡载荷压力峰值急剧减小。在以往研究爆炸气泡与自由液面相互作用时,主要考虑参数γf的影响,较少考虑浮体结构物的存在对自由液面升高的影响。由图11可知,在初始时刻,由于气泡内部高压远大于周围环境压力,流场中压力升高,使得液面升高。气泡膨胀时,气泡内部压力急剧减小,并低于周围环境压力,就会产生一个吸力,使得液面高度下降。在气泡溃灭至最小体积时,气泡内部压力再次增大,使得气泡在再次膨胀时,液面高度再次上升。在固定γf的情况下,随着γs的增大,结构对气泡的Bjerknes作用减弱,气泡更趋向于球形,液面的抬升增大,体现了结构物对液面高度的影响。
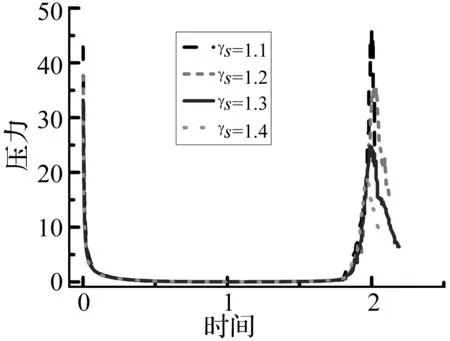
图10 不同γs下结构底部中心点压力曲线Fig.10 The time history of maximum pressure on the bottom of box at different γs

图11 不同γs下,结构中部与液面交接点处液面高度的时间历程Fig.11 The time history of maximum free surface elevation at different γs
图12给出不同γs下气泡体积的时间历程曲线,表1给出不同γs下气泡脉动周期。从图12和表1中可以看出,在气泡膨胀阶段,γs对气泡体积影响不大。在气泡溃灭阶段,随着γs的增大,气泡体积减小的速度增大,即气泡溃灭越快,气泡的脉动周期越小。

表1 不同γs下气泡脉动周期

图12 不同γs下气泡体积的时间历程曲线Fig.12 The time history of bubble volume at different γs
5.2固定γs=1.1时,不同γf的影响
图13给出固定爆点与结构之间的距离γs=1.1时,爆点与液面距离γf=1.8,1.75,1.7,1.6下 (药量分别为59.2 kg, 64.5 kg, 70 kg, 84 kg),气泡最大体积时的图形。由于气泡在膨胀阶段的形态与图9所示差别不大,就不再次赘述,仅给出气泡在最大体积的情况。从图可以看出,气泡顶部均出现扁平现象,说明气泡的形状主要受γs的影响即附近的结构物决定。

表2 不同γf下结构物中心点处的压力峰值
图14和图15分别给出了不同γf下气泡体积和液面高度的时间历程曲线。从图14知,γf对气泡体积影响很小,即此时气泡形状主要受结构物影响,自由液面的作用微小。由图15知,液面高度曲线的趋势同图11,均是随着气泡膨胀,液面升高;气泡收缩时,液面下降,并且液面的高度随着γf的减小而增大。在以往研究气泡作用下,结构物的载荷时,主要关注爆点与结构物的距离参数,对于自由液面的作用研究较少。表2给出了不同γf下,气泡载荷作用在结构物底部中心处的压力峰值。可知随着γf的减小,压力峰值减小,对结构的破坏作用减弱。当γf=1.6增至γf=1.8,气泡载荷压力峰值下降8.7%。主要是由于液面的升高消耗了气泡部分能量。

γf=1.8 t=0.963 9 γf=1.75 t=0.963 4 γf=1.7 t=0.962 9 γf=1.6 t=0.961 7图13 γs =1.1,不同γf情况下,爆炸气泡与附近浮体结构在气泡最大体积时的图形Fig.13 The evolution of bubble near floating structure at different γf when γs =1.1
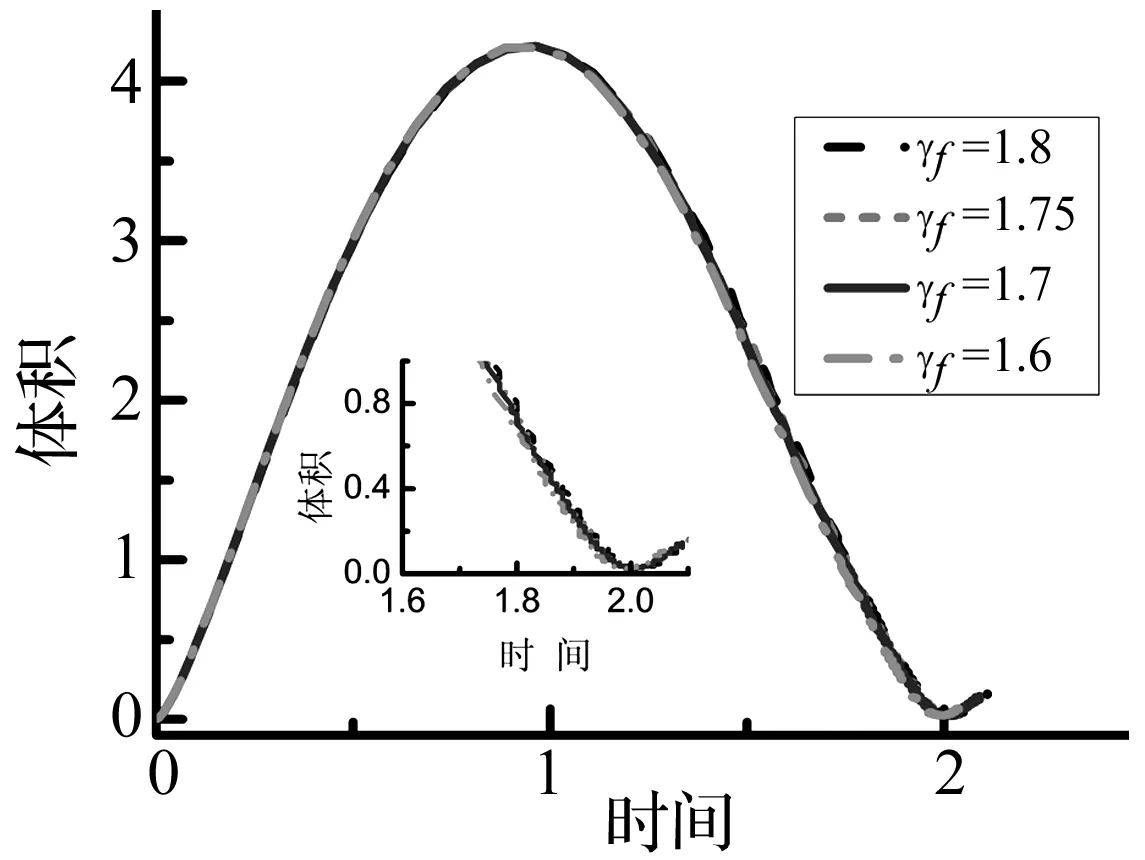
图14 不同γf下气泡体积的时间历程曲线Fig.14 The time history of bubble volume at different γf

图15 不同γf下,结构中部与液面交接点处液面高度的时间历程Fig.15 The time history of maximum free surface elevation at different γf
5.3刚体运动的影响
在上面计算中,结构物被视为固定结构。然而在实际应用中,结构的运动响应会影响气泡的运动特征,而气泡运动的变化也将反过来影响结构上的载荷等其他参数。因此,需要综合考虑结构和气泡的耦合运动才能准确预测结构物上的载荷和气泡运动参数。这里主要研究固定结构和刚体运动结构分别对气泡动力学的影响。此处的计算参数为:药量为100 kg, 深度H=12 m,Rm=5.59 m,ε=334.88,δ=0.5,R0=0.096,γf=2.14,γs=1.14。
图16给出了气泡与固定和运动方箱在气泡体积膨胀至最大和收缩至最小体积时的图形以及结构物底部在气泡最小体积时的压力云图。从图中可知,对于固定方箱,当气泡体积最大和溃灭至最小时,气泡距离结构底部距离均较刚体运动情况时的近,这是由于结构在气泡载荷下运动响应造成的。
从方箱底部的压力云图上可看出,固定方箱底部的高压区域要大于运动方箱的底部区域,说明固定方箱受到爆炸气泡产生的更大区域的载荷。从第一次气

图16爆炸气泡与固定或刚体运动浮体结构的演化过程Fig.16 The evolution of bubble near fixed or rigid movement floating structure
泡脉动周期分析,刚体运动结构的气泡脉动周期小于固定结构的气泡脉动周期,说明结构的运动响应会加速气泡的溃灭。
图17给出了固定和运动结构时,结构中部与液面交接点处液面高度的时间历程曲线,曲线的规律同图11和图15,仅是固定结构的液面高度要明显大于运动结构的液面高度。图18给出了固定和运动方箱的底部中心点处的压力曲线。其中,固定结构的压力为36.48,运动结构压力为27.49,压力峰值减弱了24.6%,主要是由于结构的运动吸收了部分爆炸的能量。图19给出了刚体运动结构的重心的运动曲线,由图可知,在气泡膨胀阶段,在初始高压的作用下结构向上运动,在气泡达到最大体积时,气泡内部压力低于环境压力,会对结构产生向下的吸力,在惯性的作用下,结构会继续向上运动。气泡溃灭时,周围流场向气泡流动,使得结构向下运动,随着气泡的反弹,结构再次向上运动。


图17 不同结构特征下,结构中部与液面交接点处液面高度的时间历程Fig.17Thetimehistoryofmaximumfreesurfaceelevationatdifferentstructuralcharacteristics图18 不同结构特征下结构底部中心点压力曲线Fig.18Thetimehistoryofmaximumpressureonthebottomofboxatdifferentstructuralcharacteristics图19 刚体运动结构重心在气泡载荷下的时间历程曲线Fig.19ThetimehistoryofCGofstructureatbubbleload
6结论
本文采用三维边界积分法模拟了气泡在自由面和浮体附近的运动。并通过计算研究了爆点与自由液面的距离γf,爆点与结构的距离γs,结构的运动特征对气泡,结构和液面的影响,并得出以下结论:
(1) 当γf=1.8固定时,随着γs的增大,作用在结构底部中心点的压力峰值急剧减小,液面高度增大,气泡溃灭时,气泡体积收缩速度加快,因此气泡脉动周期减小,在最大气泡体积时,结构物对气泡的作用减小,使气泡更趋于球形。
(2) 当γs=1.1固定时,随着γf的减小,液面高度增大,结构物底部中心点压力峰值降低,但对气泡体积和脉动周期影响不大,在气泡最大体积时,气泡形态差别不大,说明此时气泡形态主要受参数γs的影响。
(3) 针对不同的结构运动模型,比如结构做刚体运动时,由于结构运动吸收了部分爆炸的能量,使结构底部中心点处压力明显减弱,液面高度减小,气泡脉动周期减小。结构刚体运动的趋势为:在气泡膨胀时,结构向上运动,溃灭阶段,结构向下运动,反弹阶段再次向上运动。
[1] Wang Q X, Yeo K S, Khoo B C,et al.Strong interaction between a buoyancy bubble and a free surface [J]. Theoretical and Computational Fluid Dynamics, 1996, 8(1): 73-88.
[2] Li Zhang-rui, Sun Lei, Zong Zhi, et al. Some dynamical characteristics of a non-spherical bubble in proximity to a free surface [J]. Acta Mechanica, 2012; 223(11): 2331-2355.
[3] Zhang A M, Yao X L, Yu X B. The dynamics of three-dimensional underwater explosion bubble[J]. Journal of Sound and Vibration, 2008, 311(3): 1196-1212.
[4] Blake J R, Taib B B, Doherty G. Transient cavities near boundaries. Part 1. Rigid boundary [J]. Journal of Fluid Mechanics, 1986, 170: 479-497.
[5] Wang Q X. The evolution of a gas bubble near an inclined wall [J]. Theoretical and Computational Fluid Dynamics, 1998, 12(1): 29-51.
[6] Zhang A M, Yao X L, Feng L H. The dynamic behavior of a gas bubble near a wall [J]. Ocean Engineering,2009,36(3): 295-305.
[7] 李健, 林贤坤, 荣吉利,等. 近壁面水下爆炸气泡运动的数值计算研究 [J]. 振动与冲击, 2014, 33(15): 200-205.
LI Jian, LIN Xian-kun, RONG Ji-li, et al.Dynamic behavior of a bubble near a rigid wall in underwater explosion [J]. Journal of Vibration and Shock, 2014, 33(15): 200-205.
[8] Kalumuch K M, Duraiswami R, Chahine G L. Bubble dynamics fluid-structure interaction simulation by coupling fluid BEM and structural FEM codes [J]. Journal of Fluids and Structures, 1995, 9(8): 861-883.
[9] Klaseboer E, Hung K C, Wang C,et al.Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure [J]. Journal of Fluid Mechanics, 2005, 537: 387-413.
[10] Zhang A-man, Yao Xiong-liang. Interaction of underwater explosion bubble with complex elastic-plastic structure[J]. Applied Mathematics and Mechanics, 2008, 29: 89-100.
[11] Li Zhang-rui, Sun Lei, Zong Zhi. Numerical analysis of gas bubbles in close proximity to a movable or deformable body [J]. Archive of Applied Mechanics,2013,83(12):1715-1737.
[12] Gong S W, Khoo B C. Transient response of stiffened composite submersible hull to underwater explosion bubble [J]. Composite Structures, 2015, 122: 229-238.
[13] 牟金磊, 朱锡, 黄晓明,等. 水下爆炸气泡载荷在加筋板塑性变形中的作用 [J]. 振动与冲击, 2010,29(5): 74-77.
MOU Jin-lei, ZHU Xi, HUANG Xiao-ming, et al. Effect of underwater explosion bubble on plastic displacement of stiffened plates [J]. Journal of Vibration and Shock, 2010,29(5): 74-77.
[14] Klaseboer E, Khoo B C, Hung K C. Dynamics of an oscillating bubble near a floating structure [J]. Journal of Fluids and Structures, 2005, 21(4): 395-412.
[15] Blake J R, Gibson D C. Growth and collapse of a vapour cavity near a free surface [J]. Journal of Fluid Mechanics, 1981, 111: 123-140.
[16] 姚熊亮, 张阿漫. 简单 Green 函数法模拟三维水下爆炸气泡运动[J]. 力学学报, 2006, 38(6): 749-759.
YAO Xiong-liang, ZHANG A-man. Simulation of the motion of three-dimensional underwater explosion bubble using simple green function method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006,38(6):749-759.
[17] Cole R H. Underwater explosions [M]. New Jersey: Princeton University Press, Princeton, 1948.
[18] Wilkerson S A. A boundary integral approach to three dimensional underwater explosion bubble dynamics [D]. Maryland: Johns Hopkins University, 1990.
[19] Klaseboer E, Fernandez C R, Khoo B C. A note on true desingularisation of boundary integral methods for three-dimensional potential problems [J]. Engineering Analysis with Boundary Elements, 2009, 33(6): 796-801.
[20] Zhang Y L, Yeo K S, Khoo B C, et al. Three-dimensional computation of bubbles near a free surface [J]. Journal of Computational Physics, 1998, 146(1): 105-123.
[21] Wang Q X. Numerical simulation of violent bubble motion[J]. Physics of Fluids,2004,16(5):1610-1619.
[22] Zhang Y L, Yeo K S, Khoo B C. 3D jet impact and toroidal bubbles [J]. Journal of Computational Physics,2001,166(2): 336-360.
[23] Wang C, Khoo B C, Yeo K S. Elastic mesh technique for 3D BIM simulation with an application to underwater explosion bubble dynamics [J]. Computers & Fluids, 2003,32(9):1195-1212.
[24] Goldstein H. Classic Mechanics [M]. New York: Addison-Wesley,1980.
[25] Chahine G L, Kalumuck K M, Hsiao C T. Simulation of surface piercing body coupled response to underwater bubble dynamics utilizing 3DYNAFS, a three-dimensional BEM code [J]. Computational Mechanics,2003,32(4/5/6):319-326.
[26] Brujan E A, Pearson A, Blake J R. Pulsating, buoyant bubbles close to a rigid boundary and near the null final Kelvin impulse state [J]. International Journal of Multiphase Flow, 2005, 31(3):302-317.
The interaction of underwater explosion bubble dynamics and a floating structure
WANG Jia-xia1, ZONG Zhi1,2, ZHOU Li1, JIANG Ming-zuo3
(1. School of Naval Architecture, Dalian University of Technology, Dalian 116024, China;2. State Key Laboratory of Structural Analysis for Industrial, Dalian University of Technology, Dalian 116024, China;3. School of Control Science and Engineering, Dalian University of Technology, Dalian 116024, China)
The evolution of an underwater explosion bubble beneath a floating structure is numerically simulated using a three-dimensional (3D) boundary integral method (BIM) in an inviscid, incompressible and irrotational flow. The effect of a free surface on bubble dynamics is also considered. The present method is well validated by comparing the numerical simulations with the experimental results. For a free-floating structure, the distance between the bubble and the free surface, the distance between the bubble and the structure and two dynamic responses (fixed and rigidly moving) are separately investigated to research the interaction of the bubble, the floating structure and the free surface. Their influence on bubble dynamics and the pressure on the structure and the free surface are especially concerned.
underwater explosion bubble; boundary integral method; floating structure; rigid body motion
10.13465/j.cnki.jvs.2016.12.007
国家重点基础研究发展规划(973计划)(2013CB036101;2010CB832704);国家自然科学基金创新群体项目(51221961);国家自然科学基金面上项目(51279030;51379033)
2015-04-15修改稿收到日期:2015-06-23
王加夏 男,博士生,1988年生
宗智 男,教授,博士生导师,1964年生
O353
A
