安装误差对变刚度系数的复合行星轮系均载特性的影响分析

朱伟林， 巫世晶， 王晓笋， 周　璐， 张海波， 何　融

(1.武汉大学 动力与机械学院,武汉　430072; 2.中国北方车辆研究所 车辆传动重点实验室,北京　100072)

安装误差对变刚度系数的复合行星轮系均载特性的影响分析

朱伟林1， 巫世晶1， 王晓笋1， 周璐1， 张海波1， 何融2

(1.武汉大学 动力与机械学院,武汉430072; 2.中国北方车辆研究所 车辆传动重点实验室,北京100072)

以复合行星齿轮传动系统为对象，采用集中参数法，建立多自由度平移-扭转耦合非线性动力学模型。该模型在综合考虑轴承支承刚度、时变啮合刚度、齿侧间隙和齿轮安装误差的基础上，研究安装误差位置及其相位角对系统均载特性的影响。研究结果表明：中心构件的安装误差对系统产生均等的周期性影响，行星轮的安装误差会导致行星轮出现持续偏载或者均载现象；中心构件安装误差的相位角对系统均载系数没有影响，而行星轮安装误差的相位角对系统有影响，且沿切向分布时，影响最大。

复合行星轮系;轴承支撑刚度;时变啮合刚度;安装误差;均载特性

与简单行星齿轮传动系统相比，复合行星齿轮传动系统具有多种功率传递流，且结构紧凑、传动比大、承载能力强，被广泛应用于车辆船舶、航空航天、能源开发等领域。然而在实际应用中，由于齿轮安装误差的存在，使得行星齿轮受力不均等，进而导致系统出现偏载、振动和噪声，影响系统的可靠性以及使用寿命。

国内外学者对行星轮系的均载特性进行了相关的理论和实验研究，Hidaka等[1]在20世纪80年代以简单行星轮系为对象，从静力学角度分析了系统传递误差与均载系数的关系。自20世纪90年代开始，Kahraman[2-4]先后在考虑误差和刚度的情况下，分析了行星轮系的动力学均载问题，并对系统的均载特性进行了试验，同时对Ravigneaux式复合轮系进行了模态分析。Singh等[5-6]分别用不同的方法研究了制造误差对行星齿轮静态均载特性的影响。陆俊华等[7]研究了误差对简单轮系动态均载性能的影响。Guo[8]通过解析法和有限元法分析检查了复合轮系的非线性动力学行为，并对各参数灵敏度，稳定性以及齿轮的啮合刚度进行了分析。巫世晶等[9-10]分析了综合误差、齿侧间隙以及啮合刚度对某复合轮系动态特性的影响。叶福民等[11]分析了齿侧间隙对非等模数非等压力角简单行星齿轮系统均载特性的影响。

以上研究内容基本都是针对简单轮系的均载性能分析或者复合轮系的动态性能分析，而复合轮系不同构件的安装误差位置以及相位角对系统均载性能的影响还少有报道。本文基于集中参数理论，建立了拉维娜式复合行星齿轮传动系统的多自由度平移-扭转耦合非线性动力学模型，模型考虑了轴承的支撑刚度、各啮合副的时变啮合刚度、齿侧间隙以及安装误差。研究了系统的均载性能，分析了系统在安装误差作用下的均载特性变化规律，对复合行星齿轮传动系统的分析设计以及优化提供了理论依据，具有指导工程实际的意义。

1系统动力学模型的建立

1.1齿轮动力学模型

复合行星齿轮传动系统结构简图见图1(a)，系统包括太阳轮s，行星架c，内齿圈r1、r2和两种行星轮an、bn，(n=1,2，…，N),N为行星轮组数。该复合行星轮系具有多种功率流传递路线，本文中将内齿圈r1固定，太阳轮s和内齿圈r2分别作为输入输出构件。利用集中参数法对系统进行动力学建模，将一对啮合齿轮等效为弹簧-阻尼系统[12]，考虑所有构件的平移和扭转方向的自由度，其动力学模型见如图1(b)。

图1　系统动力学模型图Fig.1 The dynamic model of the system

图1中：下标s、c、r1、r2、an、bn分别表示系统的十个构件；san、r1an、r2bn、anbn分别为各类啮合副；kj、bj、ej、cj(j=san、r1an、r2bn、anbn)分别为时变啮合刚度、齿侧间隙、啮合误差和啮合阻尼；ki和kit(i=s、c、r1、r2、an、bn)分别为构件的平移支承刚度和扭转支承刚度；θi为构件的扭转角位移，规定逆时针方向为正。系统基本参数见表1。

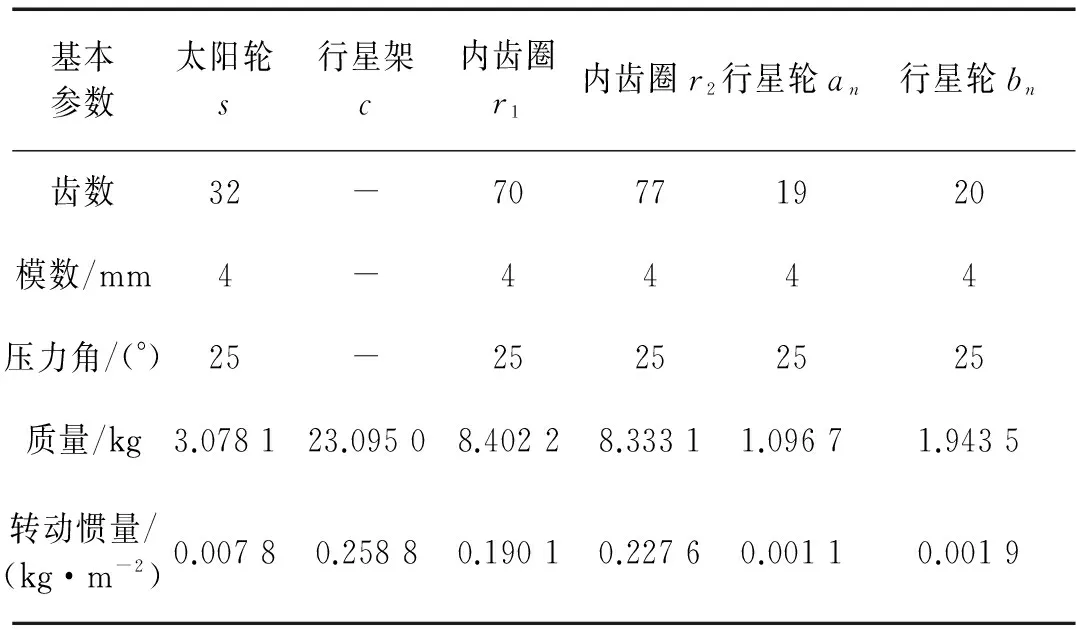
表1　复合行星轮系基本参数

1.2滚动轴承动力学模型

轴承的刚度通常被用来作为衡量齿轮传动系统构件支撑刚度的一个重要指标，本文以深沟球轴承为研究对象，对齿轮支撑刚度的计算模型进行分析。滚动轴承由外圈、内圈、滚动体及保持架组成，其刚度定义为轴承内外套圈产生单位相对弹性位移量所需要的外加负荷。假定轴承内外圈分别与旋转轴和轴承座刚性连接，滚动体之间等距排列且为纯滚动，轴承变形为滚动体与滚道之间的接触变形，则轴承所受径向力的载荷分布图见图2[13]。

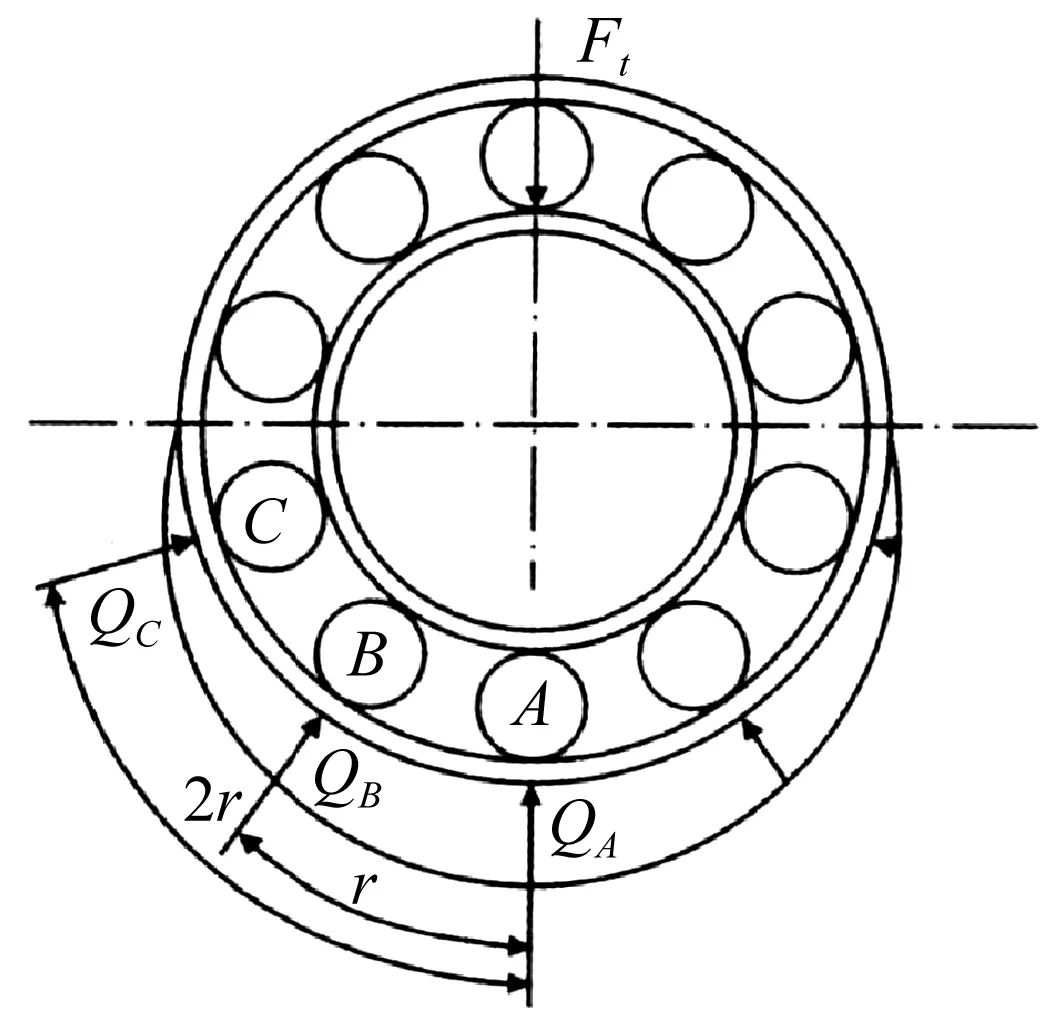
图2　滚动轴承受径向力载荷分布图Fig.2 The radial load distribution of a rolling bearing

由文献[14]可知，根据Stribeck理论计算载荷分布，求得图2中最大承载钢球所受的径向载荷为

(1)

式中：Fr为轴承所受的外部径向载荷，QA、QB、QC为钢球承受的径向载荷，γ=2π/Z为相邻两钢球之间的夹角，Z为钢球的数量。

根据赫兹弹性接触理论求得，径向载荷作用下轴承内外圈的径向趋近量为

(2)

由此可得深沟球轴承的刚度系数为

(3)

根据K(Fr)的表达式可以得知，深沟球轴承的刚度不仅与轴承的基本参数(球数、求径、沟道曲率半径和内外圈沟底半径)有关，还与轴承所受的载荷有关，由于齿轮传动过程中，啮合力是时变波动的，所以，轴承所受的载荷也是随着时间变化的，故对于同一个轴承其刚度随着时间的变化而变化，可以将其等效为时变刚度系数的硬弹簧。以本系统中的深沟球轴承6213和6020为例进行计算，当系统输入扭矩为2 000 N·m，太阳轮输入转速为1 800 r/min，系统中轴承所受径向载荷由偏载大小决定，其所受径向载荷为0～105N时与径向变形的变化关系曲线见图3，由于系统中齿圈所用为非标准轴承，故此处未作计算，参考文献[9]中取1×109N/m。

图3　滚动轴承径向变形与载荷关系图Fig.3 The relationship between radicalload and deformation for the rolling bearing

1.3时变啮合刚度动力学模型

齿轮传动系统中齿轮啮合的重合度通常>1，齿轮在啮合过程中同时参与啮合的轮齿对数则发生单齿和双齿啮合的周期性交替变化，因此齿轮副的啮合刚度也会随时间做周期性的变化。本文基于势能原理求解齿轮啮合刚度[15-17]，将轮齿简化为齿根圆上的变截面悬臂梁，见图4(a)。

图4中各参数详见参考文献[15]，将啮合齿轮的轮齿变形视作沿啮合力F作用方向的弹簧，在啮合力F作用下，储存在啮合齿轮中的弹性势能分别是：赫兹势能Uh，弯曲势能Ub，径向压缩变形能Ua、剪切变形能Us以及齿轮基体的弹性变形势能Uf。这五种势能分别可以表示为:

(4)

式中：Kh、Kb、Ka、Ks，Kf分别为沿啮合方向与轮齿变形相对应的赫兹刚度、弯曲刚度、径向压缩刚度、剪切刚度以及齿轮基体变形刚度。

根据赫兹接触理论以及弹性力学和材料力学中的梁变形理论，可求得各刚度为:

(5)

式中各参数详见参考文献[15]，综合上述轮齿弯曲变形、剪切变形、轴向压缩变形、赫兹接触变形以及轮体变形对应的啮合线上等效刚度，外啮合齿轮副单齿啮合刚度可表示为:

(6)

式中：脚标1和2分别代表齿轮啮合副中参与啮合的两个齿轮。

当一对齿轮的两对轮齿同时参与啮合时，啮合副总的有效啮合刚度可表示为

KE=

(7)

式中：i=1为第一对轮齿啮合，i=2为第二对轮齿啮合。以本文中齿轮系统模型参数计算求得各啮合副相位差为0时，在两个完整周期内的综合时变啮合刚度如图4(b)所示，由计算结果可知，由于一个系统内相啮合的齿轮模数相同，故其不同啮合副周期相等，同时内啮合齿轮副重合度高，其双齿啮合区间大于单齿啮合区间，且平均啮合刚度比外啮合副要大。

图4　时变啮合刚度分析及结果图Fig.4 The figures of the analysis and the result of the time-varying meshing stiffness

1.4安装误差动力学模型

在齿轮传递过程中，误差的存在会使得系统出现偏载、磨损等现象，齿轮的安装误差是齿轮传动误差的重要组成部分，研究安装误差对系统均载性能的影响具有重要的意义。太阳轮s的安装误差模型如图5(a)所示，将安装误差As映射到啮合副san上的等效位移为：

3）虽然环湖地区已经打响了生态旅游的旗号，但是宣传工作不尽人意，调查问卷了解到7%的游客没有接触到政府部门有关生态旅游的宣传。当地居民对生态旅游的理解只停留在口号上，不付诸实践，部分居民表示并未参与宣传中所谓的生态旅游活动。多数人未认识到生态旅游的重要性，环湖地区生态旅游观念未深入人心。在面对当地居民的经济生活发展需求、生态环境保护以及环湖地区旅游发展等矛盾时，兼顾各方利益的治理措施更显匮乏。在处理当地居民原生态生活习俗与游客旅游体验的关系时，目前管理者尚无行之有效的措施。

As-san=Assin(-ωct+αs+γs-ψan)

(8)

式中：αs和ψan分别表示太阳轮的压力角和第n个行星轮a的位置角，ψan=2π(n-1)/3。

同理，其他构件(an、bn、r1、r2)的安装误差映射到相应啮合线上的等效位移为：

(9)

式中：ν1、ν2、ν3为两类行星轮an和bn所构成的几何角度，见图5(b)，γi为安装误差的相位角。

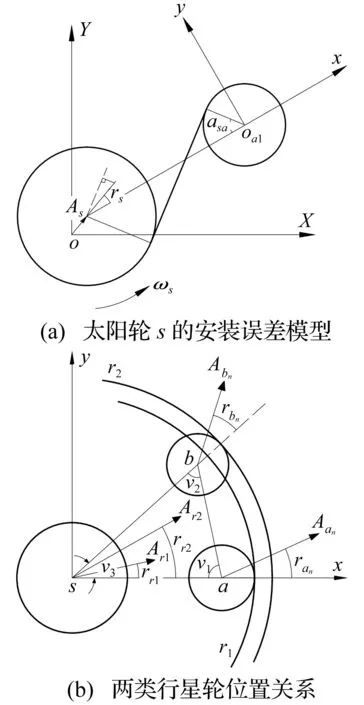
图5　安装误差分析模型Fig.5 The analysis model of the position error

2动力学方程及均载系数

2.1动力学方程

取系统各构件的横向位移xi，纵向位移yi以及扭转位移ui共30个自由度为复合行星轮系的广义坐标。

q={xsysusxcycucxr1yr1ur1

xr2yr2ur2xanyanuanxbnybnubn}T

(10)

则等效在各啮合线上的相对位移为：

(11)

利用第二类拉格朗日方程，将动态支撑刚度以及时变啮合刚度代入方程组，并引入齿侧间隙非线性分段函数，计入系统阻尼力，可以得到系统的平移-扭转动力学方程。

(12)

2.2均载系数定义

行星齿轮传动系统中，用均载系数来衡量与同一个中心轮相啮合的几个行星轮之间的受力情况，其在一个啮合周期内可以描述为：

(13)

式中Fsan、Fr1an、Fr2bn、Fanbn为各啮合副之间的啮合力，该力是随着时间做周期性变化的，故求解出的均载系数同样是时间的周期性变化曲线，为了更方便的描述系统不同行星轮之间载荷的分配情况，取其最大值作为系统中该啮合副的均载系数。则系统在整个运动周期中的均载系数表示为：

(14)

3系统均载特性分析

本文以图1中的复合行星轮系为对象进行建模求解，研究在综合考虑轴承支承刚度，时变啮合刚度和齿侧间隙多种激励因素的情况下，齿轮安装误差的位置以及相位角对系统均载特性的影响。其中，太阳轮输入扭矩为2 000 N·m，大齿圈负载扭矩为4 545.13 N·m，太阳轮输入转速1 800 r/min，齿侧间隙为20 μm，各安装误差幅值均为20 μm，误差相位角为0。

3.1安装误差位置对均载系数的影响

为了研究安装误差位置对系统均载特性的影响，保持其他参数不变，安装误差分布在太阳轮、内齿圈和行星轮的情况下，仅改变安装误差存在的位置，即不同构件存在安装误差时，系统啮合副san的均载系数变化情况见图6，通过计算，除幅值和周期不同外，系统其他啮合副的均载特性曲线变化趋势同图6中趋势一样，限于篇幅原因，其他啮合副均载系数变化情况未画出，系统各啮合副的均载系数值(max)见表2。

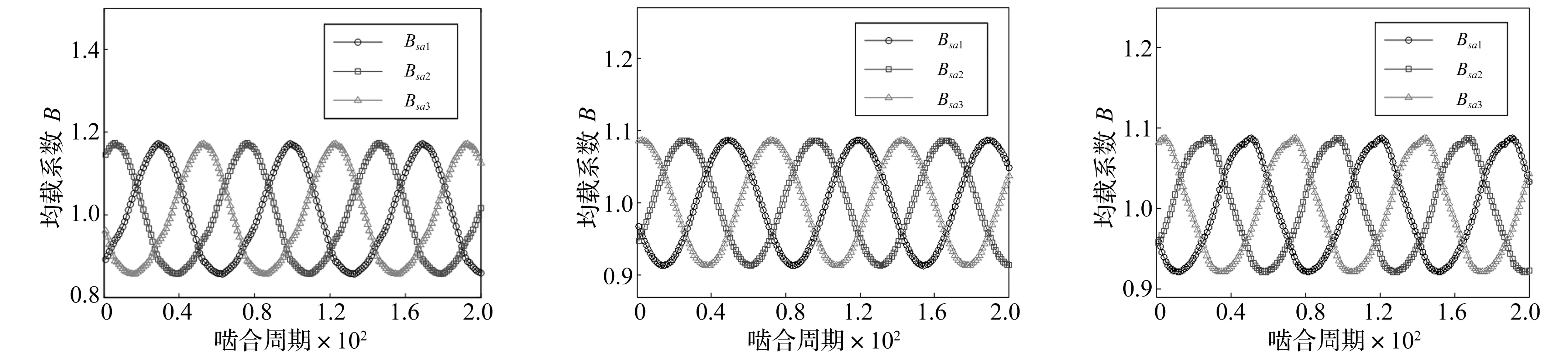
(a) 太阳轮安装误差单独作用(b) 小齿圈安装误差单独作用(c) 大齿圈安装误差单独作用

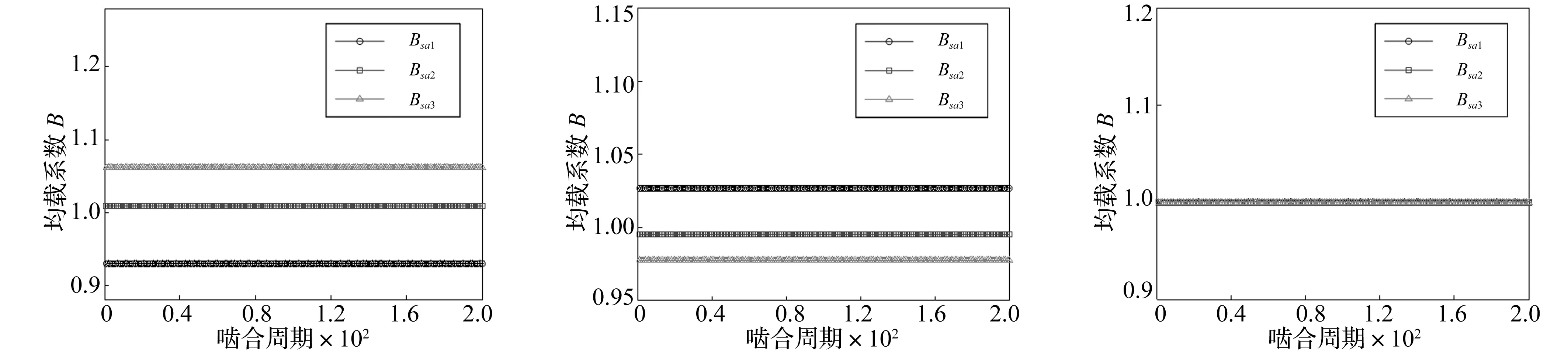
(d) 行星轮b1安装误差单独作用(e) 行星轮a1安装误差单独作用(f) 行星轮a1a2a3安装误差共同作用图6 安装误差对均载系数的影响Fig.6Influenceofpositionerrorsontheloadsharingcharacteristics

通过对比图6(a)～图6(c)可知，当安装误差分布在系统中心构件(太阳轮、内齿圈)时，系统啮合副均载系数呈现周期性变化现象，对比图6(d)～图6(f)可知，当安装误差分布在系统行星轮时，系统啮合副均载系数为定值，出现持续偏载或均载现象。当三个行星轮以相同的安装误差作用时，系统均载系数为1，各行星轮均匀受载。出现此现象的原因是当系统中心构件存在安装误差时，误差激励会随着构件的旋转对不同的行星轮产生周期性影响，而行星轮存在安装误差时，误差激励始终作用在该行星轮存在的啮合副，当三个行星轮均存在同样的安装误差时，则其产生的作用一样，故图6(f)中均载系数为1。同时，通过式(9)安装误差映射到相应啮合线上的等效位移形式可知，中心构件安装误差对等效位移的影响形式中含有ωct时间项，会随着时间对啮合副产生均等的周期性影响，而行星轮安装误差影响形式不随时间变化，为定值，故均载系数也为定值。

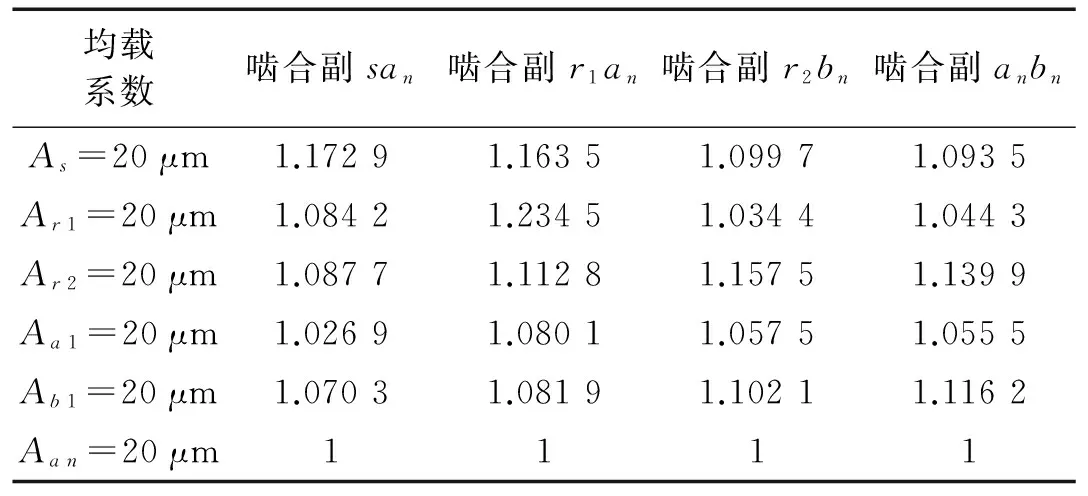
表2　不同构件安装误差下的系统均载系数最大值

表2详细列举了安装误差分布在不同构件时，系统各个啮合副的均载系数值，由表2可知，中心构件存在安装误差时，与该中心构件相关联的啮合副均载系数比其他三个啮合副更大，而行星轮存在安装误差时，系统四个啮合副的均载系数相对较平均，没有出现特别大或者特别小的，这是因为中心构件只与一个啮合副相关联，而行星轮最少与两个啮合副相关联，这是由于当中心构件存在安装误差时，其引起的偏载必须首先经过直接关联的啮合副传递到其他啮合副，故该啮合副偏载更严重，而行星轮则经过几个啮合副同时传递，各啮合副均载系数相对平均，所以在工程应用中，应该首先控制中心构件的安装误差，从而提高系统运行的平稳性。

3.2安装误差相位角对均载系数的影响

为研究安装误差相位角对于系统均载性能的影响作用，同样需保持其他因素不变，仅将安装误差相位角作为控制变量进行分析计算。当中心构件安装误差为20 μm，相位角为0°～180°时，系统均载系数(max)见表3，内齿圈安装误差相位角的变化对系统均载系数的影响同太阳轮一致，故此处仅列出太阳轮安装误差相位角对系统均载系数的影响。行星轮安装误差分别为10 μm、20 μm和30 μm，相位角从0°～180°时，系统均载系数见图7，经过计算两种行星轮安装误差相位角对系统均载性能影响趋势一致，此处仅画出行星轮an误差相位角变化对啮合副san均载性能影响的趋势图。

表3　太阳轮安装误差相位角对均载系数的影响

图7　行星轮安装误差相位角对均载系数的影响Fig.7 Influence of the phase angle of the position error of the planetary gear a1 on the load sharing coefficient

由表3可知,中心构件安装误差的相位角对均载系数没有影响，这是由于中心构件的安装误差会随着其旋转依次作用于各行星轮。故而其相位角的变化，不会引起系统均载系数的改变。由图7可知，行星轮安装误差相位角对系统均载系数有影响，系统均载系数在行星轮安装误差相位角0°～180°内呈中心对称分布，相位角为90°时，即误差沿切向分布时，其均载系数最大，这是由于行星轮的安装误差不会随着其旋转而发生变化，当安装误差切向分布时，误差在啮合线上投影的等效位移最大，故其对系统均载性能产生的影响最大。

4结论

本文采用集中质量法，建立了复合行星齿轮传动系统平移-扭转耦合动力学模型，根据第二类拉格朗日方程推导了系统的微分动力学方程，该模型综合考虑了动态轴承支承刚度，时变啮合刚度、齿侧间隙以及齿轮安装误差，分析了构件的安装误差以及系统负载扭矩对系统均载特性的影响，得到了以下结论：

(1) 轴承支承刚度与轴承的基本参数(球数、求径、沟道曲率半径和内外圈沟底半径)和轴承所受的载荷有关，可以将其等效为变刚度系数的硬弹簧。

(2) 中心构件的安装误差对系统各个啮合副产生均等的周期性影响，行星轮的安装误差会使某个行星轮出现持续的偏载，系统的均载系数为定值，当三个行星轮的安装误差一样时，系统呈现均载现象。

(3) 中心构件安装误差对其直接关联的啮合副影响较大，行星轮安装误差对系统多个啮合副均有影响，各啮合副均载系数相对较平均。

(4) 中心构件的安装误差相位角对系统均载性能没有影响，行星轮安装误差相位角对系统均载系数有影响，且在相位角为90°时，系统均载性能最差。

[1] Hidaka T, Sugimoto N, Ishida T. Effects of errors of elements on load distribution in planetary gears with various load equalizing mechanisms[J]. Transactions of the Japan Society of Mechanical Engineers,1986, 52(480):2200-2206．

[2] Kahraman A. Load sharing characteristics of planetary transmissions[J] .Mechanism and Machine Theory，1994，29(8)：1151-1165．

[3] Kahraman A. Static load sharing characteristics of transmission planetary gear sets：model and experiment[J]. SAE Transactions，1999,108(6)：1954-1963．

[4] Kahraman A. Freetorsional vibration characteristics of compound planetary gear sets[J]. Mechanism and Machine Theory, 2001, 36(8): 953-971．

[5] Singh A．Application of a system level model to study the planetary load sharing behavior[J] ． Journal of Mechanical Design，2005，127：469-476.

[6] Bodas A，Kahraman A．Influence of carrier and gear manufacturing errors on the static load sharing behavior of planetary gear sets[J]．JSME International Journal Series C，2004，47：908-915．

[7] 陆俊华，朱如鹏，靳广虎．行星传动动态均载特性分析[J]．机械工程学报，2009，45(5)：85-90．

LU Jun-hua, ZHU Ru-peng, JIN Guang-hu. Analysis of dynamic load sharing behavior in planetary gearing[J]. Journal of Mechanical Engineering, 2009，45(5)：85-90．

[8] Guo Yi-chao. Analytical study on compound planetary gear dynamics[D]．Columbus：The Ohio State University，2011．

[9] 巫世晶，刘振皓，潜波. 复合行星齿轮传动系统分岔与混沌特性研究[J]. 华中科技大学学报，2012，40(2)：9-13．

WU Shi-jing, LIU Zhen-hao, QIAN Bo. Bifurcation and chaos characteristics research for compound planetary gear train[J]. Journal of Huazhong University of Science and Technology,2012,40(2):9-13．

[10] Zhu W, Wu S, Wang X, et al. Harmonic balance method implementation of nonlinear dynamic characteristics for compound planetary gear sets[J]. Nonlinear Dynamics, 2015,81(3): 1-12．

[11] 叶福民，朱如鹏,靳广虎，等.考虑齿侧间隙的非等模数非等压力角行星齿轮系统的均载特性研究[J].振动与冲击,2015,34(11):206-211．

YE Fu-min, ZHU Ru-peng, JIN Guang-hu,et al. Load sharing characteristics of a planetary gear train system with non-equivalent modulus and pressure angle considering backlashes[J]. Journal of Vibration and Shock, 2015,34(11):206-211．

[12] 张策，机械动力学[M].北京：高等教育出版社，2008．

[13] 冈本纯三.球轴承的设计计算[M].黄志强,译，北京：机械工业出版社，2003.

[14] 万长森.滚动轴承的分析方法[M].北京：机械工业出版社，1987．

[15] Wu S, Zuo M J, Parey A. Simulation of spur gear dynamics and estimation of fault growth [J].Journal of Sound and Vibration,2008, 317(3/4/5):608-624．

[16] 万志国, 訾艳阳, 曹宏瑞, 等. 时变啮合刚度算法修正与齿根裂纹动力学建模[J]. 机械工程学报, 2013, 49(11): 153-160．

WAN Zhi-guo, ZI Yan-yang, CAO Hong-rui,et al. Time-varying mesh stiffness algorithm correction and tooth crack dynamic modeling[J]. Journal of Mechanical Engineering, 2013, 49(11): 153-160．

[17] 冯松, 毛军红, 谢友柏. 齿面磨损对齿轮啮合刚度影响的计算与分析[J]. 机械工程学报, 2015, 51(15): 27-32．

FENG Song, MAO Jun-hong, XIE You-bai. Analysis and calculation of gear mesh stiffness with tooth wear[J]. Journal of Mechanical Engineering, 2015, 51(15): 27-32.

Influence of position errors on the load-sharing characteristics of compound planetary gear sets considering the variable stiffness coefficient

ZHU Wei-lin1， WU Shi-jing1， WANG Xiao-sun1， ZHOU Lu1，ZHANG Hai-bo1， HE Rong2

(1. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China;2. Science and Technology on Vehicle Transmission Laboratory, China North Vehicle Research Institute, Beijing 100072, China)

This paper proposes a nonlinear time-varying transverse-torsional coupled model for a compound planetary gear set based on the theory of the concentrated parameter. The influence of the position errors and the phase angle on the load-sharing characteristics is analyzed by considering the bearing stiffness, the time-varying meshing stiffness and the gear backlashes of the gears. The analysis results show that the position errors of the central member will make equal periodic changes for the system, while the position errors of the planetary gears will make a sustained partial load. Meanwhile, it has no influence on the load-sharing characteristics of the system when the phase angle of the position errors exists on the central members. However, it has some influence when the phase angle of the position errors exists on the planetary gears, and the load-sharing coefficient is the largest when the phase angle is 90 degrees.

compound planetary gear sets; bearing stiffness; time-varying mesh stiffness; position errors; load sharing characteristics

10.13465/j.cnki.jvs.2016.12.012

国家自然科学基金资助项目(51375350)

2015-10-22修改稿收到日期：2015-12-28

朱伟林 男，博士生，1989年生

巫世晶 男，教授，博士生导师，1963年生

TH132

A