板带轧机机电传动系统参激非线性扭振鲁棒控制研究

韩东颖, 时培明, 赵东伟

(1.燕山大学 车辆与能源学院,秦皇岛　066004；2. 燕山大学 电气工程学院,秦皇岛　066004)

板带轧机机电传动系统参激非线性扭振鲁棒控制研究

韩东颖1, 时培明2, 赵东伟2

(1.燕山大学 车辆与能源学院,秦皇岛066004；2. 燕山大学 电气工程学院,秦皇岛066004)

建立了含参激非线性、不确定性、负载转矩的轧机机电传动系统扭振动力学模型，研究了板带轧机电机速度鲁棒跟踪非脆弱控制问题。将板带轧机机电传动系统的非线性按参数不确定性处理，通过H∞理论、Lyapunov稳定性理论和线性矩阵不等式(LMI)方法得到了通过状态反馈使得系统满足二次稳定、抑制外界干扰的充分条件;为了实现给定速度信号跟踪非脆弱控制，设计了前馈补偿器。轧机实例仿真结果验证了方法的有效性，并发现控制器的非脆弱性表现为控制器参数的鲁棒性，即可以通过控制器参数的直接选取达到板带轧机机电传动系统扭振非脆弱控制效果。

轧机；扭振；参激；非线性；鲁棒H∞

轧机传动系统是轧制设备中的关键部分，其作用是将电机产生的驱动力矩传递给轧辊，实现轧制生产，因此电机速度平稳性直接影响传动系统稳定性和产品质量。轧机传动系统模型参数具有不确定性，同时存在轧制扰动影响，轧机机电传动系统时常发生扭振现象[1-4]。轧机扭振控制引起了广泛关注，文献[5]针对轧机传动系统线性模型，基于H∞理论在传统PI控制基础上，从混合灵敏度角度设计了抑制电机速度振荡补偿器，抑制了外界干扰对电机速度、电机转矩、轴力矩的影响，但模型中仅考虑了标称值情形；文献[6]建立了基于模型匹配的轧机机电传动系统模型，通过LMI(Linear Maerix Lnequality)方法有效改善了轧机传动系统的跟踪性能，但未考虑模型的参数不确定性；在直流电机无补偿绕组或补偿绕组不能完全抵消电枢反应引起的非线性情形下，文献[7]考虑了该非线性及参数不确定性，将非线性项视为结构不确定性，在文献[8]基础上，通过求解Riccati不等式得到状态反馈控制器，并设计了前馈补偿器，较好地实现了电机速度跟踪鲁棒控制。轧机传动系统结构具有特殊性，尤其是板带轧机，由于轧制过程中接轴有倾角，将产生参激作用[9]。对这类扭振控制问题，还没有开展相关研究的报道。

本文建立了轧机机电传动系统参激非线性扭振模型，将非线性处理为参数不确定性，基于H∞理论、Lyapunov稳定性理论及LMI方法，研究了轧机机电系统中直流电机速度跟踪非脆弱控制问题，得到了系统非脆弱状态反馈控制器存在的充分条件，并设计了前馈补偿器。取得了较好的跟踪控制效果。实例仿真过程中，发现未考虑控制器摄动时，控制器自身带有一定鲁棒性，通过进一步给出的简化定理和控制器参数灵活选取，可实现含参激非线性板带轧机扭振系统速度跟踪非脆弱控制，通过实例仿真验证了方法的有效性。

1板带轧机机电传动系统含参激非线性扭振模型

板带轧机机电传动系统包含电气传动部分和机械传动部分，当研究轧机传动系统机电耦合作用时，可将传动系统简化为电气系统和机械系统两部分来研究。由于板带轧机主传动系统结构的特殊性，以及板带轧机常常进行调速、存在轧辊磨损、轧件厚度变化等，连接轴与电机和轧辊接触的部分并非水平的，即存在接轴倾角，这个倾角会引起角速度的波动，导致传动系统非线性振动。接轴倾角的变化会引起系统连接轴刚度周期性变化，使得系统的刚度表现为参数激励。

考虑参激非线性板带轧机机电传动系统结构简图见图1。

图1　含参激刚度非线性的轧机机电传动系统扭振模型Fig.1 The electrical drive system of rolling mill torsional vibration model with nonlinear parametric stiffness

图1中，D为直流电机；R为电枢绕组的电阻；U为电机电枢输入电压；L为电枢绕组的电感；J1为电机转动惯量；J2为轧辊转动惯量；ω1为电机转速；ω2为轧辊转速；T为负载转矩。KF为准周期刚度连接轴刚度的非线性形式考虑为准周期刚度[10]具体形式为：KF=K[1+ρcos(vt)+hcos(Ωt)]，其中K为等效刚度；v为与系统固有频率相关的共振频率；Ω为缓变频率；ρ为对应共振频率项的幅值系数；h为对应缓变频率项的幅值系数。

根据广义耗散系统的Lagrange原理建立模型，过程如下：对于电气传动系统部分。选择电荷q为广义坐标，则系统的电动能Vd为：

(1)

系统的电势能Vs为：

Vs=-Uq+kUω1q

(2)

设单位电荷δq流过电枢绕组的耗散能Vh为：

Vh=-Ri·δq

(3)

从而得到电阻产生的广义力矩Fr为：

Fr=-Ri

(4)

将式(1)、式(2)和式(4)代入到如下形式的Lagrange方程中：

(5)

式中：gi和Qi分别为广义坐标和广义外力矩，i=1,2。

综上可得电机侧数学模型为：

(6)

对于机械传动系统部分，选择电机端的转角θ1和轧辊端的转角θ2作为广义坐标，则该部分的动能E为：

(7)

该部分系统的势能V为：

(8)

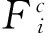
(9)

式中：pj为广义坐标，j=1,2。

本模型不考虑阻尼作用，故有：

(10)

进一步由式(9)和式(10)，得：

(11)

将式(7)、式(8)和式(11)代入式(5)，得：

(12)

又易知：

(13)

联立式(12)和式(13)，同时考虑参激非线性可得：

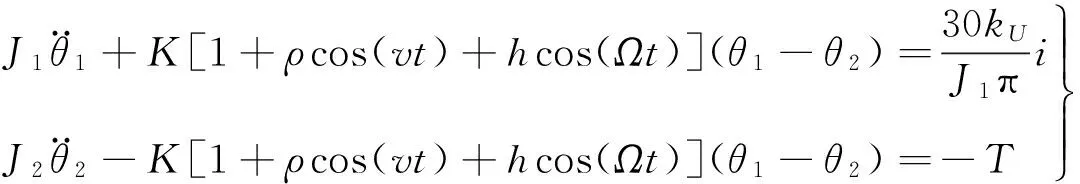
为了考察轧机接轴扭矩T12的振动情况，引入状态变量T12，即令：

T12=K[1+ρcos(vt)+hcos(Ωt)](θ1-θ2)

(15)

选择电流i、电机转速ω1、接轴转矩T12和电机转速ω2为状态变量，可得含参激刚度的板带轧机机电传动系统扭振模型为：

(16)

2参激非线性扭振鲁棒控制器设计

所建含准周期刚度的轧机机电传动系统扭振模型，基于H∞理论研究了传动系统扭振鲁棒控制问题。考虑所建立的含参激刚度的板带轧机机电传动系统扭振模型式(16)。模型中考虑了准周期刚度形式，记：

fk(v,Ω,t)=ρcos(vt)+hcos(Ωt)

(17)

为书写方便，简记fk(v,Ω,t)为fk，则式(17)进一步表示为：

(18)

(19)

将式(19)写成矩阵形式为：

(20)

将式(20)写成由字母简单表示为：

(21)

式中：

视Kfk为刚度K的参数摄动，即ΔC。暂不考虑常数项B1T对系统状态的影响，该影响可由控制输入进行前馈补偿。考虑外界扰动信号w对系统的影响，则系统模型式(21)可以写为：

(22)

式中：假设ΔC=EΣ(t)F。其中，E、F为适宜维数矩阵；Σ(t)为Lebesgue可测未知函数矩阵，且ΣT(t)×Σ(t)≤I，∀t。

对系统进行鲁棒控制的目标之一，是使系统在存在外界干扰时满足如下干扰抑制指标：

‖z‖2≤γ‖w‖2

(23)

式中：γ>0;∀w∈L2;z(t)为评价输出信号;w(t)为干扰输入信号;其属于L2空间。并设评价输出信号的具体形式为：

z(t)=Cx+Du

(24)

式中：系数矩阵C、D满足CTD=0。

联立式(22)和式(24)，得增广受控系统模型如下:

(25)

3参激非线性扭振鲁棒控制器求解

对增广受控系统模型式(25)，引入线性静态状态反馈控制器K，即令：

u=Kx

(26)

则式(25)变为如下闭环形式：

(27)

选定Lyapunov函数为二次型形式，即：

V(x,t)=xT(t)Px(t)

(28)

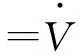
φ=xT(A+BK+ΔC)TPx+xTP(A+BK+ΔC)x+

γ2wTw<0

(29)

将ΔC的具体形式代入上式，有：

(30)

EΣ(t)F+FTΣT(t)ET≤λPEETP+λ-1FTF

(31)

将式(30)和式(31)代入式(29)，使式(29)成为一个充分性不等式：

ATP+PA+KTBTP+PBK+λPEETP+

λ-1FTF+CTC+KTDTDK<0

(32)

式(32)左乘、右乘矩阵P-1，得：

P-1AT+AP-1+P-1KTBT+BKP-1+

λEET+λ-1P-1FTFP-1+P-1CTCP-1+

P-1KTDTDKP-1<0

(33)

注意到P-1=PT，设P-1=X，KP-1=Y，则式(33)变为：

XAT+AX+YTBT+BY+λEET+

λ-1XFTFX+XCTCX+YTDTDY<0

(34)

利用Schur补引理将上式等价转化为如下矩阵不等式：

(35)

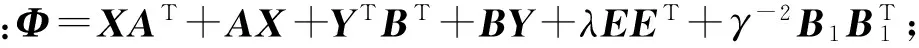
将上述推导过程整理得到如下定理。

定理3.1给定常数γ>0，对于式(25)，存在状态反馈控制器K，使得闭环系统无干扰时二次稳定；零初始条件下，满足干扰抑制指标式(23)的一个充分条件为，存在常数λ>0，正定对称矩阵X和矩阵Y，满足如下矩阵不等式：

(36)

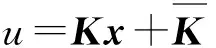
(37)

4实例分析

以某型冷连轧机传动系统相关参数[12]为实例参数：主电机额定功率1 500 kW，额定电压938 V，额定电流1 720 A，额定转速290 r/min，电机转子的转动惯量为J1=1 552 kg·m2，轧辊的转动惯量为J2=1 542 kg·m2，kU=29 N·m/A，R=0.031 4 Ω，L=0.000 3 H，K=5.93×106，T=29 100 N·m，ν=1，Ω=0.01，h=0.04，ρ=0.01。

考虑计算可得式(22)的相关矩阵数值如下：

令λ=10 000，γ=1时，由LMI工具箱中feasp求解器，可求得状态反馈控制器为：

K=

[-0.231 2 -432.705 5 -0.011 0 198.564 4]

(38)

图2为给定速度为27.23 rad/s时电机速度的响应曲线;图3为其横向放大图，可见实际电机速度信号在控制输入的作用下，能快速平稳的跟踪给定速度信号。

图4为在给定电机速度为27.23 rad/s时，连接轴扭矩T12的响应曲线，图5为图4的横向放大图，由图4可知，扭矩是从零开始迅速加大，达到一定值后逐渐减小，直到平缓稳定，仿真结果表明控制效果良好。

图6和图7分别为在给定电机速度为27.23+sin(6.28t) rad/s时，电机速度和连接轴扭矩的响应曲线。由图6可知，电机速度信号在给定信号的第一个波谷到来之前实现了信号的跟踪，响应曲线快速随给定信号波动，实现了动态跟踪；图7为在给定电机速度信号为27.23+sin(6.28t) rad/s时的扭矩响应曲线。

图2 ω=27.23rad/s时的电机速度响应曲线Fig.2Themotorspeedresponsecurveatω=27.23rad/s图3 ω=27.23rad/s时的电机速度响应曲线放大图Fig.3Themotorspeedresponseamplificationcurveatω=27.23rad/s图4 ω=27.23rad/s时的连接轴扭矩响应曲线Fig.4Theconnectingshafttorqueresponsecurveatω=27.23rad/s

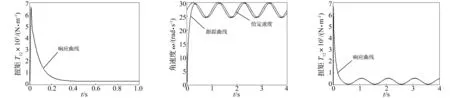
图5 ω=27.23rad/s时的连接轴扭矩响应曲线放大图Fig.5Theconnectingshafttorqueresponseamplificationcurveatω=27.23rad/s图6 给定时变信号下的电机速度响应曲线Fig.6Themotorspeedresponsecurveundertimevaryingsignal图7 给定时变信号下的连接轴扭矩响应曲线Fig.7Theconnectingshafttorqueresponsecurveundertimevaryingsignal

图8和图9为给定速度信号为27.23 rad/s，假设外界干扰信号为幅值是负载转矩1/10的正弦信号，即2 910 sin(6.28t)情形，电机速度和连接轴扭矩响应曲线，曲线波动很小，效果良好。

图10～图13为给定阶跃信号下，电机速度的跟踪曲线图及其放大图和连接轴扭矩的响应曲线图及其放大图，由图可见，实现了电机速度对给定速度信号的快速跟踪，除开始由一次速度波动外，整个过程平稳。连接轴扭矩的波动得到了有效的抑制；图14～图17为给定时变信号和存在扰动信号两种情形下的电机速度跟踪曲线和连接轴扭矩响应曲线。仿真结果表明，在给定控制输入下，实现了动态信号的有效跟踪和连接轴扭振的有效抑制。

图8 扰动信号下的电机速度响应曲线Fig.8Themotorspeedresponsecurveunderdisturbancesignal图9 扰动信号下的连接轴扭矩响应曲线Fig.9Theconnectingshafttorqueresponsecurveunderdisturbancesignal图10 ω=2.723rad/s时的电机速度响应曲线Fig.10Themotorspeedresponsecurveatω=2.723rad/s

图11 ω=2.723rad/s时的电机速度响应曲线放大图Fig.11Themotorspeedresponseamplificationcurveatω=2.723rad/s图12 ω=2.723rad/s时的连接轴扭矩响应曲线Fig.12Theconnectingshafttorqueresponsecurveatω=2.723rad/s图13 ω=2.723rad/s时的连接轴扭矩响应曲线放大图Fig.13Theconnectingshafttorqueresponseamplificationcurveatω=2.723rad/s

图14 动态给定信号下的电机速度响应曲线Fig.14Themotorspeedresponsecurveunderdynamicsignal图15 动态给定信号下的连接轴扭矩响应曲线Fig.15Theconnectingshafttorqueresponsecurveunderdynamicsignal图16 扰动信号下的电机速度响应曲线Fig.16Themotorspeedresponsecurveunderdisturbancesignal

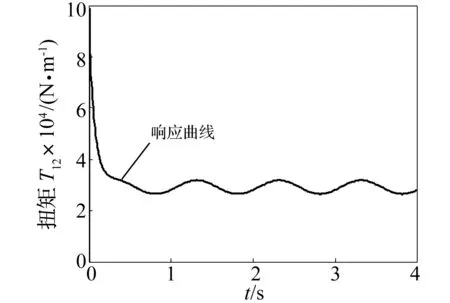
图17　扰动信号下的连接轴扭矩响应曲线Fig.17 The connecting shaft torque response curve under disturbance signal

对于系统模型发生摄动情形，控制效果与标称情形类似。

5结论

针对含参激刚度非线性的板带轧机机电传动系统扭振模型，基于H∞理论和Lyapunov稳定性理论，设计了实现系统鲁棒稳定性和鲁棒性能的状态反馈控制器，同时设计了前馈补偿器，消除了稳态误差。最后通过实例仿真，可知所设计的控制器和补偿器可以通过控制器参数的直接选取，实现板带轧机机电传动系统扭振非脆弱控制，验证了算法的有效性。

[1] 刘浩然, 张业宽, 李晓梅, 等. 轧机非线性传动系统冲击扭振的研究与抑制[J]. 振动与冲击, 2010,29(7):189-193.

LIU Hao-ran, ZHANG Ye-kuan, LI Xiao-mei, et al. Investigation and suppression of impact torsional vibration of a rolling mill’s nonlinear drive system [J]. Journal of Vibration and Shock, 2010, 29(7): 189-193．

[2] Shi Pei-ming, Li Ji-zhao, Jiang Jin-shui, et al. Nonlinear dynamics of torsional vibration for rolling mill’s main drive system under parametric excitation [J]. Journal of Iron and Steel Research International, 2013, 20(1):7 -12．

[3] 侯东晓,刘彬,时培明,等.两自由度轧机非线性扭振系统的振动特性及失稳研究[J].振动与冲击, 2012, 31(3):32-36．

HOU Dong-xiao, LIU Bin, SHI Pei-ming, et al. Vibration characteristics of 2-DOF nonlinear torsional vibration system of rolling mill and its conditions of instability[J]. Journal of Vibration and Shock, 2012, 31(3):32-36．

[4] 时培明, 夏克伟, 刘彬, 等. 含间隙多自由度轧机传动系统非线性扭振动力特性[J]. 机械工程学报,2012,48(17): 57-64．

SHI Pei-ming, XIA Ke-wei, LIU Bin, et al. Research on dynamics behaviors of rolling mill’s nonlinear torsional vibration of multi-degree-of-freedom main drive system with clearance [J]. Journal of Mechanical Engineering，2012，48(17): 57-64．

[5] 张登山, 李华德.H∞扭振抑制控制器在热连轧机组上的应用[J]. 电工技术学报, 2006, 21(1): 92-97．

ZHANG Deng-shan, LI Hua-de.H∞Vibration suppression controller in the hot continues rolling mill machine [J]. Transactions of China Electrotechnical Society,2006,21(1):92-97．

[6] 张瑞成, 童朝南, 李伯群. 基于LMI方法的轧机主传动系统机电振动H∞控制[J]. 北京科技大学学报,2006,28(2):179-184．

ZHANG Rui-cheng, TONG Chao-nan, LI Bo-qun. H∞control based on LMI for electromechanical vibration of a rolling mill main drive system [J]. Journal of University of Science and Technology Beijing, 2006, 28(2): 179-184．

[7] 方一鸣, 王乐, 王益群, 等. 具有电枢反应非线性不确定性的直流电机速度鲁棒跟踪控制[J]. 中国电机工程学报, 2003, 23(5): 136-139．

FANG Yi-ming, WANG Le, WANG Yi-qun, et al. The research of speed robust tracking control on DC motor considering the nonlinear of armature reaction[J]. Proceeding of the CSEE,2003, 23(5): 136-139．

[8] 申铁龙.H∞控制理论及应用 [M]. 北京: 清华大学出版社, 1996．

[9] 闫晓强, 刘丽娜, 曹曦, 等. CSP轧机万向接轴弯扭耦合振动[J]. 北京科技大学学报,2008,10(10):1158-1162．

YAN Xiao-qiang, LIU Li-na, CAO Xi. et al. Coupling of lateral and torsional vibration for the spindle of a CSP mill[J]. Journal of University of Science and Technology Beijing, 2008, 10(10): 1158-1162．

[10] 李纪召. 板带轧机主传动非线性参激扭振系统的稳定性及控制研究[D]. 秦皇岛：燕山大学, 2012．

[11] Xu S, Lam J, Yang C. Quadratic stability and stabilization of uncertain linear discrete-time systems with state delay[J]. Systems & Control Letters, 2001, 43(2): 77-84．

[12] 方一鸣, 路金波, 刘仙,等. 冷连轧机张力系统H∞混合灵敏度鲁棒控制器设计[J]. 系统仿真学报, 2004, 16(8): 1812-1815．

FANG Yi-ming,LU Jin-bo, LIU Xian, et al. Design ofH∞mixed sensitivity robust controller for tension system of tandem cold rolling mill[J]. Journal of System Simulation,2004,16(8):1812-1815．

Study on robust control for parametric excitation nonlinear torsional vibration of a strip-rolling mill’s mechanical and electrical drive system

HAN Dong-ying1, SHI Pei-ming2, ZHAO Dong-wei2

(1. College of Vehicles and Energy, Yanshan University, Qinhuangdao 066004, China;2. College of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China)

While considering parametric excitation nonlinearity, uncertainty and load torque, the nonlinear torsional vibration dynamic model of a mechanical and electrical transmission system in a strip-rolling mill is built. The problem of the strip-rolling mill’s motor-speed robust tracking and non-fragile control of the DC motor is studied. As the nonlinearity of the strip-rolling mill’s mechanical and electrical drive system is translated into parameter uncertainty, the sufficient condition that lets the system attain quadratic stability and outside-disturbance attenuation is obtained using H∞theory, Lyapunov stability theory and the LMI method. In order to achieve the given speed-signal tracking and non-fragile control, a feedforward and compensatory controller is designed. The results of the real strip-rolling mill’s simulation example verify the effectiveness of the proposed method, and the non-fragility of the controller is reflected as the controller’s parameter robustness. This means that the effect of the torsional vibration non-fragile control of the strip-rolling mill’s mechanical and electrical drive system can be fulfilled by choosing the parameters of the controller directly.

rolling mill; torsional vibration; parametric excitation; nonlinear; robustH∞

10.13465/j.cnki.jvs.2016.12.001

国家自然科学基金(51005196)；河北省自然科学基金(E2012203194)

2015-05-12修改稿收到日期：2015-06-19

韩东颖 女，博士，副教授，1978年生

TM341

A