2K-H行星轮系的平移扭转模型建立与非线性动态特性分析

周　璐， 巫世晶， 李　景, 王晓笋， 朱伟林， 李小勇

(武汉大学 动力与机械学院，武汉　430072)

2K-H行星轮系的平移扭转模型建立与非线性动态特性分析

周璐， 巫世晶， 李景, 王晓笋， 朱伟林， 李小勇

(武汉大学 动力与机械学院，武汉430072)

为探讨2K-H行星轮系的非线性动态特性，建立了考虑时变啮合刚度、综合啮合误差和齿侧间隙等强非线性因素的平移-扭转耦合动力学模型，并推导了系统的无量纲化18自由度运动学微分方程组。通过相轨线、Poincare图和时间历程曲线分析了啮合频率、啮合阻尼和齿侧间隙对系统分岔与混沌特性的影响。结果表明：随着啮合频率的增大，系统由激变途径进入混沌状态；增大啮合阻尼可以使系统摆脱混沌运动进入周期运动状态；在高速轻载时，系统的动态响应对间隙非常敏感，而在某些间隙范围内，响应只有幅值的改变，动力学行为不发生变化。

2K-H行星轮系；非线性；平移-扭转耦合；动态特性

与普通定轴齿轮传动相比，行星齿轮传动最显著的优点在于其功率分流特性，其“大传动比，高载荷”的特点使其广泛应用于航空、船舶、重型车辆等机械传动系统领域。轮系的动力学特性能够从原理上反映系统的振动和噪声情况，然而，在轮系实际运行过程中，灾难性事故的发生往往是由系统的异常振动(非工频振动)引起的，因此，有必要采用非线性振动方法来研究齿轮系统的动力学问题。孙智民等[1]提出齿侧间隙的存在会使2K-H行星轮系呈现强的非线性动力学行为，孙涛等[2]建立了传动轮系的弯扭耦合动力学模型，并用谐波平衡法对其进行了求解和动态特性分析。杨绍普等[3]利用谐波平衡法研究了齿轮副的非线性动力学特性，并建立了模型的解的统一形式。Kahraman[4-7]给出了具有间隙和外部激励作用下的非线性系统振动实验结果，并证实了亚谐波共振和混沌现象的存在。李同杰等[8-9]在考虑行星轮系齿侧间隙和误差的基础上，建立了轮系的非线性纯扭转模型，并研究了转速和间隙对系统分岔特性的影响。纯扭转模型是一种仅考虑构件的扭转振动、自由度较少的精简模型，一般用于动态设计场合，而平移扭转模型还考虑了构件沿与轴线垂直的正交平面内的两个平移振动自由度，是一种便于估算系统动态特性的更准确的模型。

目前的研究大都只考虑轮系中各构件的扭转自由度，本文还考虑了构件的水平和垂直振动自由度，以2K-H行星轮系为例，对其建立18自由度的无量纲化平移-扭转动力学微分方程模型，并采用数值方法对系统的动力学分岔与混沌特性随啮合频率、啮合阻尼和齿侧间隙的变化情况进行了分析，为进一步研究系统参数对行星轮系动态特性的影响提供理论基础，对于改善行星传动系统的动力学性能、实现动态设计和故障诊断具有重要的理论研究意义和工程应用价值。

1平移扭转非线性动力学建模

1.1平移扭转耦合动力学模型

本文采用集中参数模型对行星轮系进行描述，其运动简图见图1(a)，s,c,r,p分别为太阳轮、行星架、内齿圈和行星轮，将啮合齿轮对简化为弹簧阻尼系统[10-11]，图1(b)为2K-H平移-扭转耦合动力学模型：其中，OXY为固定坐标系，原点O位于行星架的回转中心，Oxy为随行星架以其理论角速度ωc等速旋转的随动坐标系，其x轴通过第一个行星轮的理论中心。

图1　2K-H行星轮系平移扭转耦合动力学模型Fig.1 Translation-torsion coupling dynamic model for 2K-H planetary gear train

图1(b)中：n为行星轮的个数，n=3;xi,yi(i=s,c,r,p1,p2,p3)表示各构件的平移振动自由度，θi(i=s,c,r,p1,p2,p3)为构件的扭转自由度；ui=rbiθi(i=s,c,r,p1,p2,p3)为构件的扭转线位移，ri,ki,mi,Ii分别表示各构件的分度圆半径、支承刚度、质量和转动惯量，rc=rs+rp,kcp为行星架对行星轮的支承刚度；cj,2bj,kj,ej分别为齿轮副的啮合阻尼、齿侧间隙、时变啮合刚度和综合啮合误差，j=sp1,sp2,sp3,rp1,rp2,rp3。

1.2时变啮合刚度

在轮齿啮合过程中，参与啮合的齿对数会发生周期性的变化，因而齿轮副的啮合刚度也是时变的。若将单个齿简化为一根弹簧，则相啮合的一对轮齿可视为一对弹簧的串联，由于直齿轮的重合度一般为1≤ε≤2，啮合过程是由一对齿啮合和两对齿啮合交替出现的，两对轮齿啮合可视为两对单齿啮合弹簧的并联(见图2)。

图2　啮合齿对的时变啮合刚度曲线Fig.2 Time-varying meshing stiffness curve for meshing teeth

在实际应用中，可用三角函数的形式来表示时变啮合刚度：

kspi=kmspi+kmspiκsin(ωm+φj)

krpi=kmrpi+kmrpiκsin(ωm+φj)

(1)

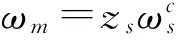
1.3综合啮合误差

在齿轮的加工和装配过程中，不可避免的会产生多种误差，综合啮合误差是行星轮系产生振动的主要内部激励之一[12]，第n路内外齿轮副综合啮合误差erpn和espn分别为：

espn=Espnsin(ωmt+φj)

erpn=Erpnsin(ωmt+φj)

(2)

式中，Erpn和Espn分别为综合啮合误差幅值，其它符号的意义同前。

1.4非线性齿侧间隙

由于润滑的需要以及使用过程中的磨损，啮合轮齿对之间会存在齿侧间隙，使啮合副出现接触-脱离-再接触的反复冲击现象[13]，对系统的均载和动态特性产生较大的影响。

通常用间隙非线性函数f(δ)表示齿侧间隙存在时啮合力与齿轮副沿啮合线上相对啮合位移之间的关系，f(δ)为分段函数，表达式如下：

(3)

式中，bj为半齿侧间隙，δj为啮合副的相对啮合位移。

相对啮合位移是定义在随动坐标系下的，指齿轮由于振动在啮合线上的线位移之和，规定各项位移符号的规则为：假定图1中标明的逆时针方向为各构件的运动方向，若构件的振动使啮合线压缩，则符号为正，反之为负，各啮合副的相对啮合位移为：

δspn=(-(xs-xpn)sin(φspn)+(ys-ypn)cos(φspn)+

δrpn=(-(xr-xpn)sin(φrpn)+(yr-ypn)cos(φrpn)+

(4)

式中:φspn和φrpn分别为太阳轮-行星轮啮合副以及内齿圈-行星轮啮合副的方向角;φspn=φpn-αs，φrpn=φpn

+αr。其中，αs、αr、φpn分别表示太阳轮的压力角、内齿圈的压力角以及行星轮的相位角，φpn=2π(n-1)/3。

2系统运动微分方程建立

取各构件的平移和扭转共18个自由度为行星轮系的广义坐标，即q={xs,ys,θs,xc,yc,θc,xr,yr,θr,xp1,yp1,θp1,xp2,yp2,θp2,xp3,yp3,θp3}T，系统的动势L为：

(5)

代入第二类Lagrange方程

(6)

将弹性力修正为非线性的分段函数形式，并引入阻尼，可以得到无量纲化的线位移形式的2K-H行星轮系平移-扭转耦合运动微分方程组：

(7)

(8)

(9)

(10)

3动力学特性分析

本文针对2K-H行星轮系进行分析，输入扭矩Ts=1 000 N·m，负载扭矩为Tc=3 187.5 N·m，基本参数如表1所示。

表1　2K-H行星轮系基本计算参数

表中，啮合刚度指时变啮合刚度平均值，即kmspi=kmrpi=5×1010N/m，时变啮合刚度系数取κ=0.25，支承刚度以及啮合刚度值均来源于实际应用。

3.1系统随啮合频率Ω的运动特性分析

本文采用maple数值计算软件对式(7)～(10)进行求解，取各啮合副的半齿侧间隙为bspi=brpi=40 μm，误差为Espi=Erpi=20 μm，阻尼为ξ=0.07，以啮合副δsp1为例进行分析，系统随啮合频率Ω的运动分岔图见图3，论文中各分岔图、时间历程曲线、相图和Poincare图均经过无量纲化处理。

图3中，系统的运动状态随啮合频率表现出丰富的分岔特性：当0≤Ω≤1.23，1.53≤Ω<2和Ω≥3.86时，系统处于单周期运动状态；当2≤Ω<2.3和3.08≤Ω<3.86时，系统处于多周期运动状态；当1.24≤Ω≤1.52和2.3≤Ω<3.08时，系统处于混沌状态。

图3　ξ=0.07时系统随啮合频率运动分岔图Fig.3 Movement bifurcation diagram by meshing frequency when ξ is 0.07

(a)Ω=0.6(b)Ω=1.34(c)Ω=3.44

(d)Ω=0.6(e)Ω=1.34(f)Ω=3.44

(g)Ω=0.6(h)Ω=1.34(i)Ω=3.44图4 不同啮合频率下δsp1的相图、Poincare图以及时间历程曲线Fig.4Phasediagram,Poincarediagramandtimehistoryplotofδsp1atdifferentmeshingfrequency

从图4可知,在低啮合频率时，系统为周期运动状态，当Ω=0.6时，其相图、Poincare图以及时间历程曲线如图4(a)、图4(d)、图4(g)所示，Poincare图只有一个孤立点，表明系统呈单周期运动状态；随着啮合频率的增大，系统立即进入混沌状态，当Ω=1.34时，其相图、Poincare图以及时间历程曲线如图4(b)、图4(e)、图4(h)所示,其相图呈高度无序状态，时间历程曲线中δsp1振幅的不规则跳动也显示出系统的混沌运动特征；当啮合频率继续增大时，系统由混沌运动进入双周期运动状态，当啮合频率增大到2.3时，系统又进入混沌状态，随后又从混沌状态转为多周期运动状态(如图4(c)、图4(f)、图4(i)所示，系统为周期2运动状态)，最后回归单周期运动状态。

结合图3和图4可知，当啮合频率较小时，随着Ω的缓慢变化，系统由单周期运动状态突然跃变到混沌运动，此过程呈现出“激变”特征，表明系统是通过“激变”途径进入混沌状态的。由于“激变”途径进入混沌状态一般出现在含间隙系统，因此，本文将齿侧间隙考虑在内正好与之相吻合。

由于实际运行工况较复杂，系统的啮合频率可能发生轻微的变化，当其位于分岔点时，很容易由一种运动状态突跳到另一种状态上，使系统的稳定性降低，因此需要严格控制啮合频率的范围，提高系统的稳定性。

3.2系统随啮合阻尼的运动特性分析

啮合阻尼系数对非线性系统的动态特性有着重大的影响，当啮合频率分别为1.44和2.5时，系统随阻尼系数ξ的运动分岔图分别见图5和图6。

图5　Ω=1.44时系统随阻尼系数运动分岔图Fig.5 Movement bifurcation diagram by damping coefficient when Ω is 1.44

图6　Ω=2.5时系统随阻尼系数运动分岔图Fig.6 Movement bifurcation diagram by damping coefficient when Ω is 2.5

啮合频率Ω为2.5时：当0≤ξ≤0.076时，系统处于混沌状态；当0.076<ξ≤0.134时，系统为周期2运动状态；当ξ>0.134时，系统为稳定的单周期运动状态。ξ为0.064、0.12和0.174时，δsp1的相图和Poincare图见图7。

从图5和图6可知，当阻尼系数较小时，系统为混沌运动状态，随着阻尼系数的增大，系统由复杂运动转化为周期运动。图7中不同阻尼系数下的特性图与图6的分岔图相吻合，混沌意味着系统运动状态的不可预测性和轨道的不重复性，这种跳跃反映出实际运行过程中的冲击和疲劳，因此，从避免系统出现混沌运动的角度来看，适当增加阻尼系数，可以使系统由混沌运动进入周期运动。

(a)ξ=0.07(b)ξ=0.12(c)ξ=0.174

(d)ξ=0.07(e)ξ=0.12(f)ξ=0.174图7 不同阻尼系数下δsp1的相图和Poincare图Fig.7PhasediagramandPoincarediagramofδsp1atdifferentdampingcoefficient

3.3系统随间隙的运动特性分析

齿侧间隙的存在会使轮齿啮合副之间产生冲击，影响传动系统的平稳性[14]，当啮合频率Ω=2.5，ξ=0.07时，系统随齿侧间隙bsp的分岔图如图8所示。

图8　Ω为2.5时系统随齿侧间隙的运动分岔图Fig.8 Movement bifurcation diagram by gear backlash when Ω is 2.5

从图8可知，当啮合频率为2.5，间隙较小时，系统为单周期运动，随着间隙的增大，系统逐渐转变为周期2运动状态，最后变为混沌状态。

当Ω=2.5，bsp为0、20 μm和60 μm时，δsp1的时间历程曲线图、相图以及Poincare图见图9。

图9中，不同间隙情况下，系统的各动态特性图与图8中的分岔图相对应，观察图9(a)、图9(b)、图9(c)，齿侧间隙分别为0、20 μm和60 μm时，轮齿啮合副分别为双边冲击、双边冲击和单边冲击状态，当齿侧间隙不断增大时，齿轮副将保持单边冲击状态不变。

当Ω=1时，不同齿侧间隙下δsp1的时间历程曲线和相图见图10。

(a)bsp=0(b)bsp=20(c)bsp=60

(d)bsp=0(e)bsp=20(f)bsp=60

(g)bsp=0(h)bsp=20(i)bsp=60图9 不同齿侧间隙下δsp1的时间历程曲线、相图以及Poincare图Fig.9Timehistoryplot,phasediagramandPoincarediagramofδsp1atdifferentgearbacklash

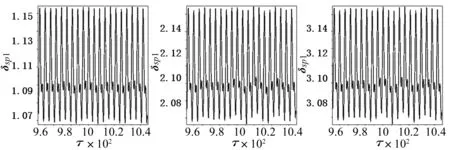
(a)bsp=0(b)bsp=10(c)bsp=20

(d)bsp=0(e)bsp=10(f)bsp=20图10 Ω=1时,不同间隙的时间历程曲线以及相图Fig.10Timehistoryplotandphasediagramofdifferentgearbacklash

从图10可知，当啮合频率Ω=1时，齿侧间隙为0时啮合副为单边冲击状态，随着间隙的增大，齿轮副仍为单边冲击状态，系统的动态特性只有量的改变，没有发生质的影响，表明此种情况下系统的响应对间隙不敏感。

4结论

(1)本文系统介绍了影响2K-H行星轮系动态特性的主要非线性因素，对其建立18自由度的平移-扭转耦合动力学模型，系统在啮合频率、阻尼和齿侧间隙3大敏感参数作用下表现出了丰富的分岔特性。

(2)啮合频率对系统的分岔特性影响非常明显，随着啮合频率的增大，系统通过激变途径由周期运动进入混沌状态，然后转变为多周期运动，最后回归为单周期运动状态；在低阻尼情况下，系统为混沌状态，随着阻尼系数的增大，系统由倍周期运动向周期运动发生转变。

(3)单一因素间隙对系统动态特性的影响难以分析，往往还取决于啮合频率和负载，在高速轻载时，系统的响应对间隙非常敏感；然而在一些特定的范围内，间隙的改变对系统的动态特性只有量的改变，没有发生质的影响。

[1] 孙智民，季林红，沈允文. 2K-H行星齿轮传动非线性动力学[J]. 清华大学学报，2003, 43(5):636-639.

SUN Zhi-min, JI Lin-hong, SHEN Yun-wen. Nonlinear dynamic for 2K-H planetary gear train[J].Journal of Tsinghua University, 2003, 43(5):636-639.

[2] 孙涛，沈允文，孙智民，等. 行星齿轮传动非线性动力学方程求解与动态特性分析[J]. 机械工程学报，2002，38(3):11-15.

SUN Tao, SHEN Yun-wen, SUN Zhi-min, et al.Nonlinear dynamic equation and dynamic characteristics analysis[J]. Journal of Mechanical Engineering, 2002,38(3):11-15.

[3] 杨绍普，申永军，刘献栋. 基于增量谐波平衡法的齿轮系统非线性动力学[J]. 振动与冲击，2005，24(3):40-42.

YANG Shao-pu, SHEN Yong-jun, LIU Xian-dong. Nonlinear dynamics of gear system based on incremental harmonic balance method[J]. Journal of Vibration and Shock,2005,24(3):40-42.

[4] Kahraman A. Load sharing characteristics of planetary transmissions[J]．Mechanism and Machine Theory，1994，29(8):1151-1165.

[5] Kahraman A. Free torsional vibration characteristics of compound planetary gear sets[J]. Mechanism and Machine Theory，2001，36:953-971.

[6] Kahraman A. Non-linear dynamics of a spur gear pair[J]. Journal of Sound and Vibration，1990，142(1):49-75.

[7] Kahraman A. Experiments on nonlinear dynamics behavior of an oscillator with clearance and periodically time-varying parameters[J]. ASME Journal of Applied Mechanics，1997, 64:217-226

[8] 李同杰，朱如鹏，鲍和云，等. 行星齿轮系扭转非线性振动建模与运动分岔特性研究[J]. 机械工程学报，2011，47(21):76-83.

LI Tong-jie, ZHU Ru-peng, BAO He-yun, et al. Modeling of torsional nonlinear vibration and movement bifurcation characteristic research for planetary train.[J]. Journal of Mechanical Engineering,2011,47(21):76-83.

[9] Guo Yi-chao，Parker R G. Purely rotational model and vibration models of compound planetary gears[J]. Mechanism and Machine Theory, 2010, 45(3): 365-377.

[10] 宋轶民，许伟东，张策，等. 2K-H行星传动的修正扭转模型建立与固有特性分析[J]. 机械工程学报，2006，42(5):16-21.

SONG Yi-min, XU Wei-dong, ZHANG Ce, et al.Modified torsional model establishment and inherent characteristic analysis for 2K-H planetary train[J]. Journal of Mechanical Engineering,2006,42(5):16-21.

[11] 巫世晶，刘振皓，潜波，等. 复合行星齿轮传动系统分岔与混沌特性研究[J]. 华中科技大学学报，2012，40(2):9-13.

WU Shi-jing, LIU Zhen-hao, QIAN Bo, et al.Bifurcation and chaos characteristics research for compound planetary gear train[J].Journal of Huazhong University of Science and Technology,2012,40(2):9-13.

[12] 张策. 机械动力学[M]. 北京：高等教育出版社，2014.

[13] 巫世晶，彭则明，王晓笋，等. 啮合误差对复合行星轮系动态均载特性的影响[J]. 机械工程学报，2015(3):29-36.

WU Shi-jing, Peng Ze-ming, WANG Xiao-sun, et al. The influence of meshing error of dynamic load characteristicfor compound planetary gear train[J]. Journal of Mechanical Engineering，2015(3):29-36.

[14] 王晓笋，巫世晶，周旭辉，等. 含侧隙非线性齿轮传动系统的分岔与混沌分析[J]. 振动与冲击，2008，27(1):53-57.

WANG Xiao-sun, WU Shi-jing, ZHOU Xu-hui,et al.With lateral clearance nonlinear bifurcation and chaos analysis of gear transmission system[J]. Journal of Vibration and Shock,2008,27(1):53-57.

Establishment of translational and torsional model and nonlinear dynamic characteristic analysis for 2K-H planetary gear trains

ZHOU Lu, WU Shi-jing, LI Jing, WANG Xiao-sun, ZHU Wei-lin, LI Xiao-yong

(School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)

To study the nonlinear dynamic characteristics of a 2K-H planetary gear train, a translation-torsion coupling dynamic model is established, taking the nonlinear factors like time-varying mesh stiffness, synthetic meshing error and gear backlash into account. The dimensionless kinematic differential equations of 18 degrees of freedom for the system are then derived. The influences of meshing frequency, damping and backlash on the system’s bifurcation and chaos characteristics are analyzed through the phase trajectory, Poincare graph and time history plot. The results show that the system will come into a chaotic state through a catastrophic way with the increase of the meshing frequency. The system can get rid of chaotic movement into a periodic motion state by increasing the damping. The dynamic response of the system is sensitive to backlash at high speeds and with a light load while the response is only a change of amplitude not a dynamic behavior in certain backlash ranges.

2K-H planetary gear train；nonlinear；transverse-torsional coupled；dynamic characteristics

10.13465/j.cnki.jvs.2016.12.011

国家自然科学基金资助项目(51375350);中国北方车辆研究所车辆传动重点实验室资助项目(20144614);多股螺旋弹簧钢丝扭动微动力学特性及磨损机理研究(2015M572193)

2015-04-16修改稿收到日期：2015-07-05

周璐 女，硕士生，1991年生

巫世晶 男，教授，博士生导师，1963年生

TH132

A