滚珠丝杠式惯容器非线性建模与参数辨识*

2016-08-03孙晓强汪少华杨晓峰

振动、测试与诊断 2016年2期

关键词：最小二乘法非线性

孙晓强，　陈　龙，　汪少华,　杨晓峰

(江苏大学汽车与交通工程学院　镇江，212013)

滚珠丝杠式惯容器非线性建模与参数辨识*

孙晓强，陈龙，汪少华,杨晓峰

(江苏大学汽车与交通工程学院镇江，212013)

摘要针对滚珠丝杠式惯容器存在的非线性力学特征，首先，分析了滚珠丝杠式惯容器的工作原理，对惯容器的主要部件进行了非线性力学分析，建立了考虑摩擦、间隙以及丝杠弹性力的惯容器非线性力学模型；然后,在数控液压伺服激振试验台上进行了惯容器的力学性能试验，得到了惯容器在不同惯容系数以及不同激振输入下的力学响应特性；最后,根据试验结果分析了摩擦和间隙对惯容器力学性能的影响，得到了便于参数辨识的惯容器力学模型结构，实现了惯容器输出力仿真与试验结果的分析和对比。结果显示，二者在一个周期内的均方根值误差不超过7%，非线性模型呈现出良好的拟合精度，证明了所述方法的可行性和有效性。

关键词滚珠丝杠式惯容器；非线性；最小二乘法；参数辨识

引言

为了在机械网络中寻找一种能够与电容严格相对应的基本元件，Smith[1]提出了惯容器(Inerter)的概念，并给出其两端点实现形式，从此，电容在与机械元件对应时不再有接地要求。随后，Smith等[2]将惯容器应用于车辆悬架中，通过优化比较多种布置形式的惯容-弹簧-阻尼(interter spring damper，简称ISD)悬架减振性能，对惯容器的隔振潜力进行了分析。2006年，一种包含惯容器的补偿装置在高性能摩托车上得到了应用，成功解决了摩托车在转向过程中的失稳问题[3]。Wang等[4-5]针对含惯容器的列车悬架进行了研究，结果表明惯容器能够有效改善列车在行驶过程中的乘坐舒适性和安全。江苏大学于2007年开展了应用惯容器的研究，证实应用惯容器能够提高车辆悬架系统的隔振性能[6-7]。

然而，上述惯容器的应用研究均是以惯容器线性数学模型为前提，忽略了惯容器实际机械结构中存在的非线性因素。文献[8]指出，间隙和非线性弹性力对惯容器的力学性能有着直接影响。文献[9]同时考虑了摩擦力这一非线性因素，建立惯容器非线性力学模型，研究了惯容器非线性对ISD悬架性能的影响。

在考虑非线性因素的影响下，笔者对滚珠丝杠式惯容器的主要部件进行了力学分析，建立了包含摩擦、间隙以及丝杠弹性力的惯容器非线性力学模型。通过试验分析了摩擦和间隙对惯容器实际力学性能的影响，并对模型中的摩擦和间隙进行了合理的简化，从而得到便于参数辨识的模型结构，基于该结构推导出惯容器输出力与惯容器两端间相对加速度之间的传递函数，并采用最小二乘递推算法对模型参数进行了辨识。仿真与试验结果对比表明，该方法呈现出良好的拟合性能，具有较高的实用价值。

1惯容器非线性模型的建立

1.1滚珠丝杠式惯容器工作原理

滚珠丝杠式惯容器的结构如图1所示，主要由便于两端吊耳焊接的圆筒(左筒和右筒)、丝杠、螺母、轴承、轴承座以及飞轮构成。

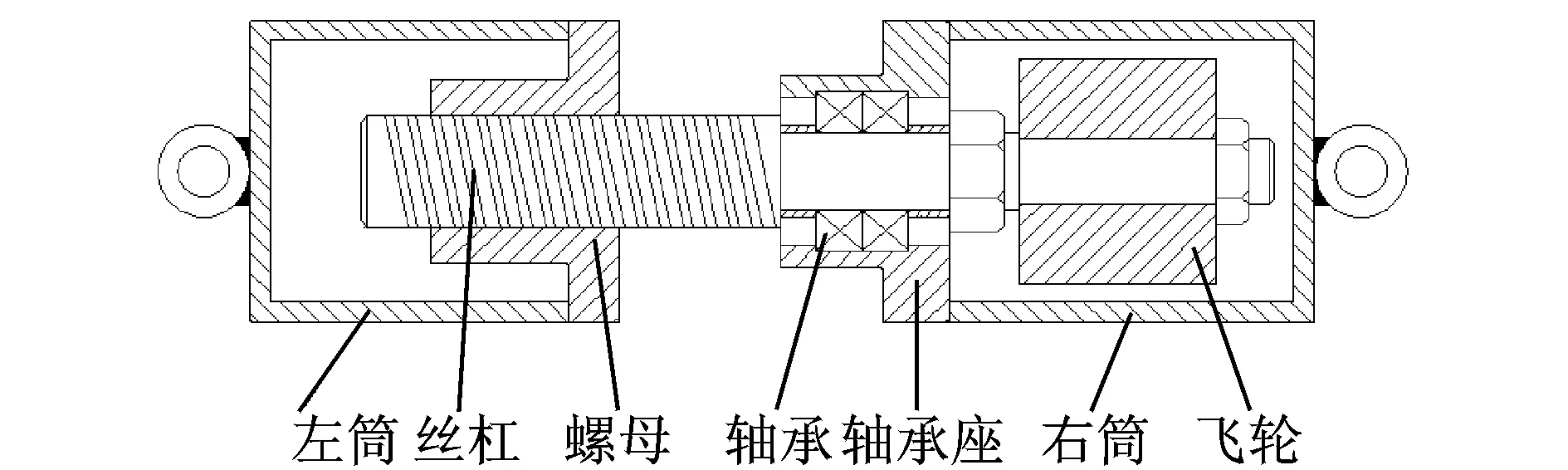
图1　滚珠丝杠式惯容器Fig.1　Ball-screw inerter

当大小相等，方向相反的力沿轴向施加于惯容器两端时，惯容器两端间便会产生相对直线位移，通过滚珠丝杠副将其转化为丝杠的旋转运动，然后通过丝杠带动飞轮旋转，从而实现飞轮转动惯量的放大，即飞轮惯性的封装。

滚珠丝杠式惯容器的理想线性动力学方程如下

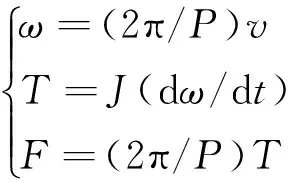
(1)

其中：ω为丝杠旋转角速度；P为滚珠丝杠副的导程；v为惯容器两端间相对速度；T为丝杠上驱动力矩；J为惯容器转动惯量；F为惯容器两端间作用力。

由式(1)可得F的表达式为

(2)

其中：b为惯容系数；a为惯容器两端间相对加速度。

通过式(2)可得惯容系数b的表达式为

(3)

惯容系数为惯容器的惯性参照，单位为kg，因此，惯容器的物理性质与一个同等质量的质量块相似。根据式(3)，惯容器对飞轮旋转过程中产生的惯性质量进行了放大，从而能够以较小的飞轮自重实现上百千克的惯性质量，为惯容器的实际工程应用提供了有利条件。

1.2主要部件的力学分析

惯容器中的非线性因素主要来源于滚珠丝杠副，因此，为建立惯容器非线性模型，考虑对螺母和丝杠进行非线性力学分析(图2)。图2中，F为惯容器两端间作用力；x1为惯容器两端间相对位移；Td为丝杠驱动力矩；x2为螺母与丝杠间力传递中螺母相对于惯容器另一端的位移；x1和x2之间的关系为x1-x2=ε，ε为惯容器中存在的间隙，主要包括丝杠和螺母之间的游隙、轴承的间隙以及两端吊耳中存在的间隙，这里集中以ε表示。

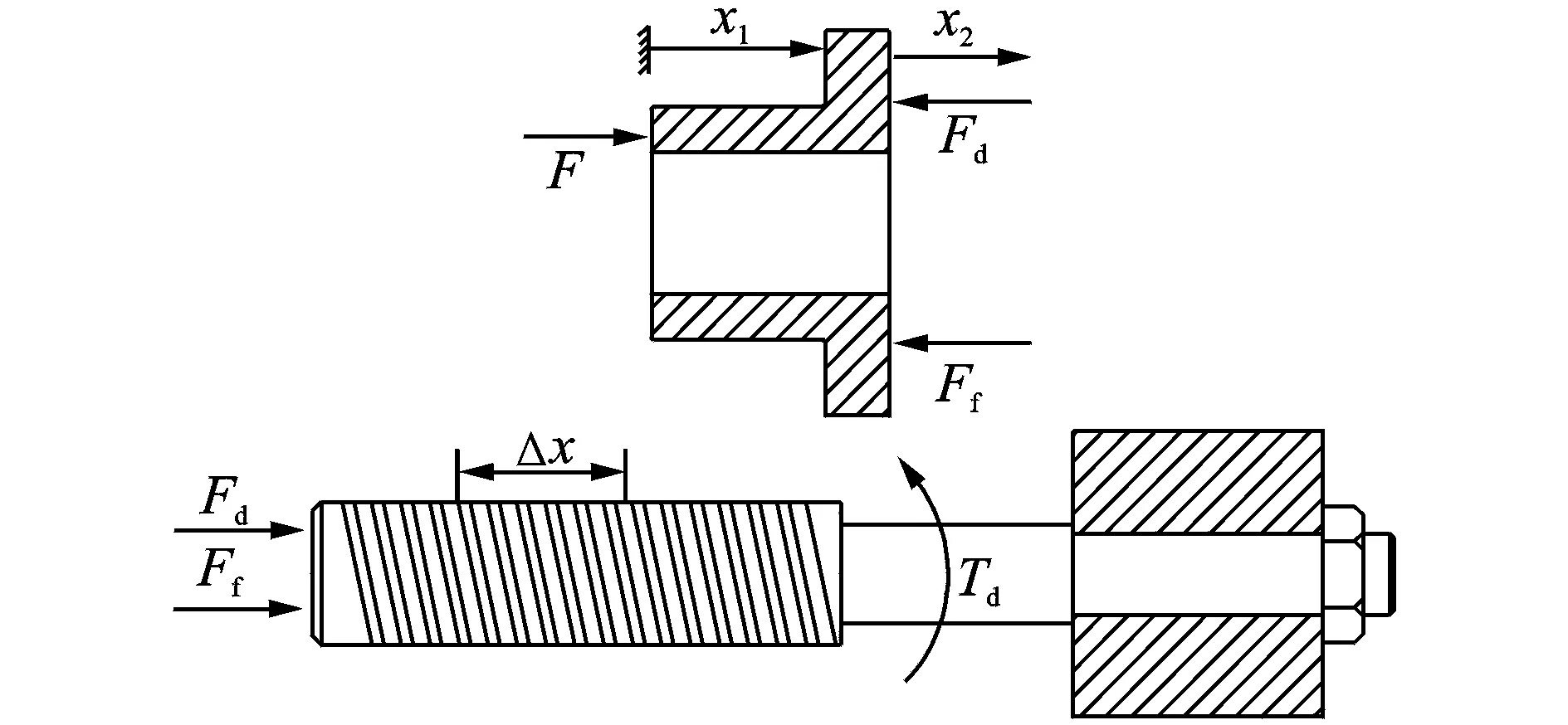
图2　螺母和丝杠的力学分析Fig.2　Mechanics analysis of nut and screw

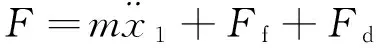
(4)

其中：m为螺母、左筒以及吊耳三者质量的集中表示；Ff为螺母与丝杠之间的摩擦力；Fd为螺母作用在丝杠上的驱动力，是丝杠对螺母的反作用力。

丝杠的轴向刚度和扭转刚度并非为理想中的无穷大，因此，丝杠在承受轴向力以及驱动力矩时会产生弹性形变。丝杠的弹性特性可以用等效刚度ke和等效阻尼ce来表示，丝杠受到的驱动力和摩擦力与其弹性形变Δx之间存在如下关系

(5)

由于丝杠中存在弹性形变，因此，螺母与丝杠间实际相对位移x3可以用式(6)表示，同时丝杠的实际旋转角度θ如式(7)

(6)

(7)

由式(2)得到，丝杠受到的驱动力和摩擦力随丝杠旋转角度θ、螺母与丝杠间相对位移x3的变化关系为

(8)

其中：J为惯容器中所有转动部件的转动惯量之和(包括丝杠本身、丝杠上的紧固螺母以及飞轮等)。

1.3非线性模型

通过上述分析，掌握了非线性因素在滚珠丝杠式惯容器力流传播过程中的影响机理，从而建立了如图3所示的惯容器简化力学模型，进而可以得到惯容器的非线性力学模型，如图4。

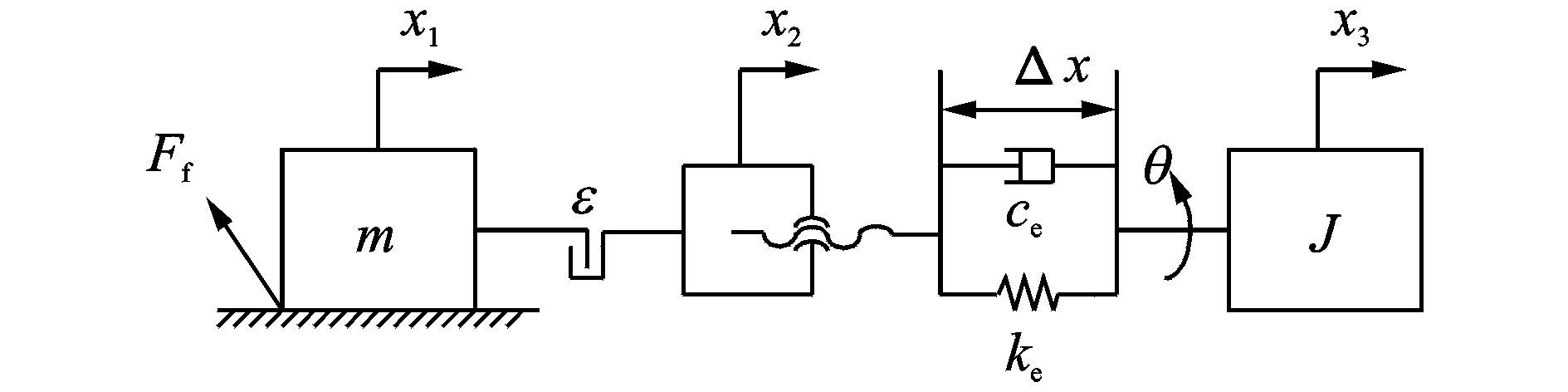
图3　滚珠丝杠式惯容器简化力学模型Fig.3　Simplified mechanics model of ball-screw inerter

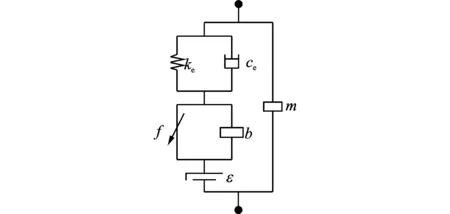
图4　滚珠丝杠式惯容器非线性模型Fig.4　Nonlinear model of ball-screw inerter

2惯容器的试验

为分析非线性因素对滚珠丝杠式惯容器实际力学性能的影响，进行了惯容器的力学性能试验。试验对象为本课题组研制的滚珠丝杠式惯容器，采用两种质量不同的飞轮，通过式(3)进行惯容系数的计算，得到相应的惯容系数分别为130和330 kg。试验设备为美国INSTRON公司生产的8800数控液压伺服激振试验台，该试验台能够支持激振头按照一定的位移要求运动，并实时观测和保存激振头的位移和载荷信号。惯容器上端固定，下端与激振头相连，试验采用正弦输入，为了防止测试力超出激振台的负荷，在高频振动时采用了较小的振幅。测试工况参数如表1所示(括号内为相应频率)。

表1　测试工况参数

通过试验获得了不同测试工况下的惯容器动态响应特性，以b=130 kg为例，当频率分别为0.1和7 Hz时，惯容器的力学响应如图5所示。各测试工况下的试验结果如表2，表中主要对比了不同激振输入下惯容器输出力的平均幅值和理论幅值以及二者之间的误差百分比。

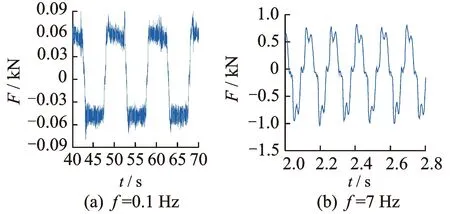
图5　惯容器的力学输出Fig.5　Mechanical outputs of inerter

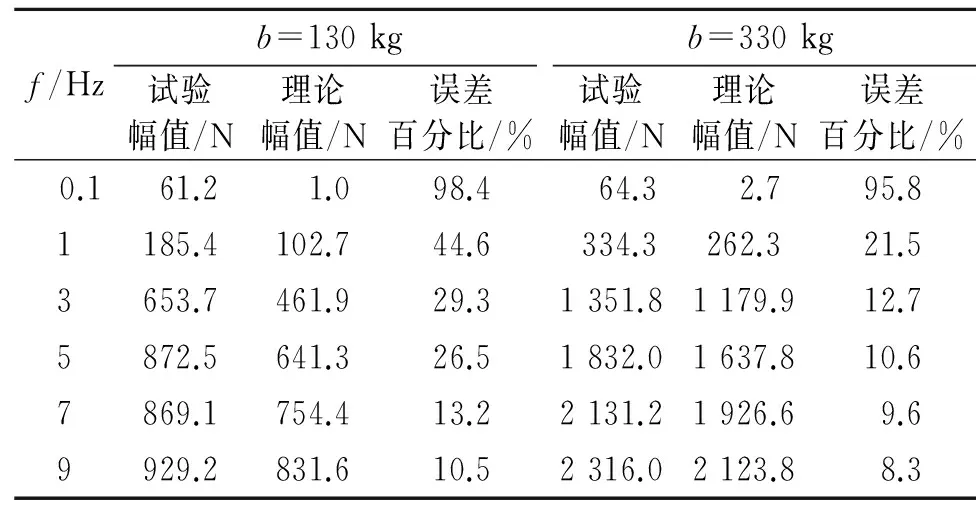
f/Hzb=130kgb=330kg试验幅值/N理论幅值/N误差百分比/%试验幅值/N理论幅值/N误差百分比/% 0.161.2 1.098.4 64.3 2.795.81185.4102.744.6334.3262.321.53653.7461.929.31351.81179.912.75872.5641.326.51832.01637.810.67869.1754.413.22131.21926.69.69929.2831.610.52316.02123.88.3

由上述试验结果发现，在部分频率下，理论值与试验值之间存在较大幅度的误差，这说明非线性因素对惯容器实际力学性能的影响不容忽视。因此，为实现非线性惯容器的力学性能预测，考虑对惯容器非线性力学模型中的相关参数进行辨识。

3模型参数辨识

由于所建惯容器力学模型中包含摩擦和间隙等非线性因素，常规的辨识方法难以对模型参数进行有效辨识，因此，进一步分析摩擦和间隙对惯容器力学性能的影响，并对模型中的摩擦和间隙进行合理的简化，从而得到便于参数辨识的模型结构。

3.1摩擦与间隙的简化

3.1.1摩擦的简化

惯容器中的摩擦主要存在于丝杠和螺母间的接触面上，且摩擦力Ff与丝杠螺母间相对运动速度v之间的关系[10]可用下式表示

(9)

其中：f0为摩擦力的幅值；sgn为符号函数(当v>0时，函数值取1；当v=0时，函数值取0；当v<0时，函数值取-1)。

在低频时，惯容器的惯性力较小，此时摩擦力占据主导地位，因此，在图5(a)中，惯容器的输出力与正弦波相差较大，呈现出方波的特征。图6为惯容系数b=330 kg，频率f=0.1 Hz时，惯容器的力学响应。结合图5和图6可以看出，当惯容系数改变时，摩擦力的幅值基本不变，因此，根据试验结果可以确定摩擦力的幅值f0为60 N，摩擦力的性质为方波，摩擦力的方向与速度方向相反。

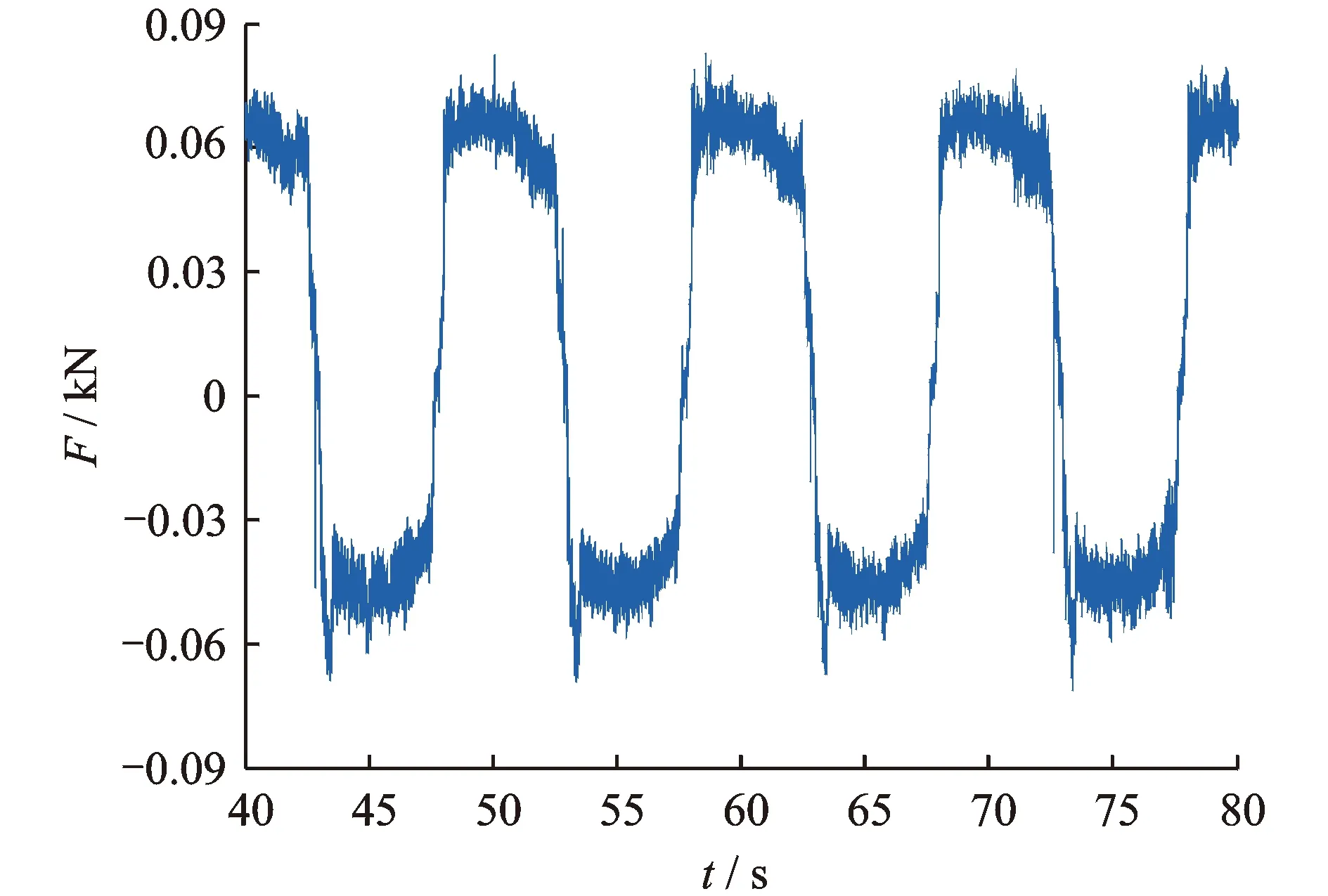
图6　惯容器的力学响应(b=330 kg，f=0.1 Hz)Fig.6　Mechanical responses of inerter (b=330 kg，f=0.1 Hz)

3.1.2间隙的简化

间隙主要会导致惯容器在高速旋转换向时产生迟滞现象，因此，当惯容器的位移方向改变时，间隙的非线性特性就会显现。由图5(b)可以看出，惯容器输出力在零值附近出现了较小幅度的波动，这正是受到了间隙的影响。因为根据惯容器位移输入与加速度输入之间的对应关系，当加速度为零时，惯容器的位移方向恰好出现了突变，因而间隙的影响在此时得以体现。基于间隙对惯容器输出力的影响幅度较小，且在研制惯容器时，对滚珠丝杠副采用了双螺母预紧，使得其中的间隙尽可能减小。因此，为了便于模型参数的辨识，忽略了间隙对惯容器力学性能的影响，即令ε= 0。

3.2惯容器输出力模型

通过对摩擦和间隙进行合理的简化，得到了惯容器输出力的简化模型，如图7所示。

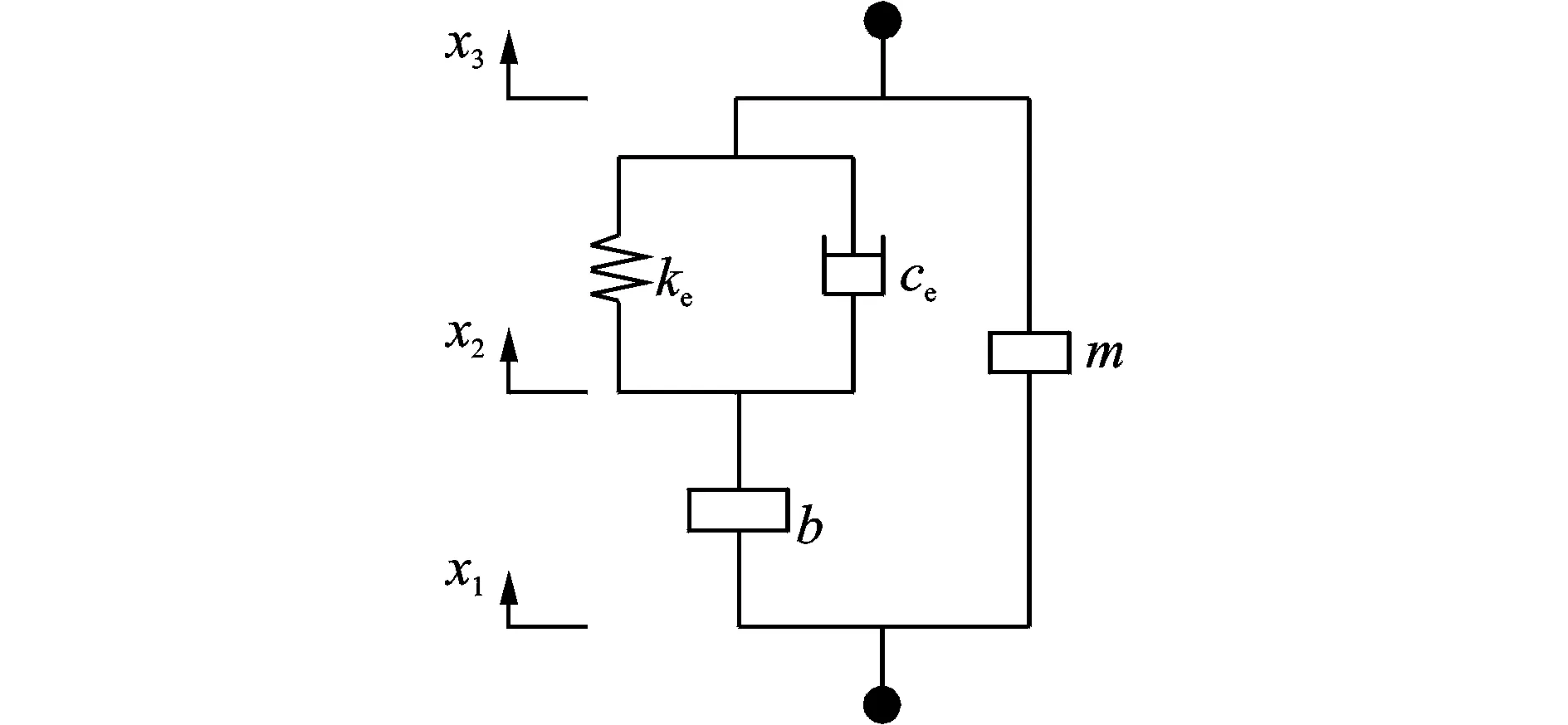
图7　惯容器输出力简化模型Fig.7　Simplified model of inerter output force

根据图7所示的模型，建立惯容器的相关动力学方程如下

(10)

(11)

由于试验时惯容器的上端固定，即x3=0，因此，以上方程可以进一步简化为

(12)

(13)

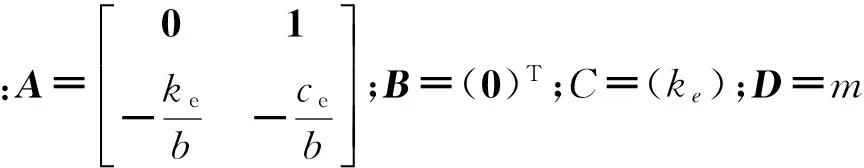
3.3模型参数辨识

通过进行惯容器的力学性能试验，获取了真实测试工况下的系统输入输出数据，在此基础上，进一步采用最小二乘递推算法对惯容器非线性力学模型中的参数进行辨识。具体参数辨识过程如下[11-12]。

1)根据系统状态方程求取系统输入与输出间的传递函数。

对式(13)进行拉普拉斯变换可得

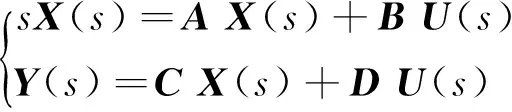
(14)

通过式(14)可得系统的传递函数为

(15)

将矩阵A，B，C，D代入上式，得到系统的传递函数进一步可表示为

(16)

2)采用双线性变换方法对连续传递函数进行离散化。

令

(17)

其中：T为采样周期。

然后将式(17)代入到式(16)中，得到传递函数的离散形式为

(18)

其中：a1，a2，a3，a4，a5，a6为待辨识的参数。

这些参数与惯容器力学模型参数之间存在如下关系

(19)

根据式(18)得到系统相应的差分方程为

a1Y(k)+a2Y(k-1)+a3Y(k-2)=a4U(k)+

a5U(k-1)+a6U(k-2)

(20)

3)根据差分方程推导系统的最小二乘格式。

将待辨识的系数移到等式右端可得

o4U(k-1)+o5U(k-2)

(21)

因此，系统输入输出的最小二乘格式为

(22)

其中:θ为待辨识的参数集合;h为样本集合;e(k)为系统采样误差。

(23)

4)根据试验数据进行模型参数辨识。

取准则函数为

(24)

4惯容器力学模型验证

为验证所建模型的准确性以及辨识方法的有效性，利用试验获取的惯容器输入输出数据对模型参数辨识。鉴于试验台只能保存惯容器的位移输入，这里借助Matlab曲线拟合工具箱Cftool对惯容器的位移输入进行曲线拟合，然后将得到的曲线方程进行差分求导便可获得惯容器的速度和加速度输入。

针对两种不同的惯容系数，分别选取部分测试工况下的试验数据，并采用前述的模型参数辨识方法对相关参数进行辨识，参数辨识结果如表3。根据表3中结果对相应的方程组进行求解，得到惯容器输出力模型的参数值如表4，其中，T为试验台保存数据的采样间隔，取为0.001 s。

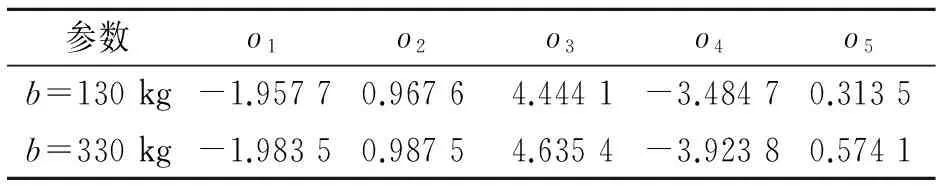
表3　参数辨识结果

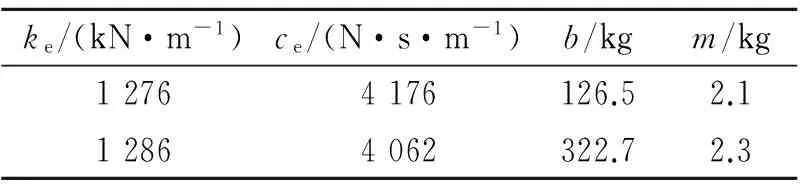
表4　惯容器输出力模型参数

从表4中可以看出，通过辨识得到的惯容系数与实际值十分接近，最大误差仅为2.7%，同时表示螺母、左筒以及吊耳三者质量的m与实际估算值2.5 kg也较为吻合，这间接证明了辨识方法以及辨识结果的准确性。根据表4最终确定丝杠的等效刚度ke为1 280 kN/m，等效阻尼ce为4 100 Ns/m。

将上述参数代入惯容器非线性力学模型中，并将拟合后得到的惯容器两端间相对速度和相对加速度作为惯容器力学模型的输入进行仿真，部分测试工况下的仿真结果与试验结果对比如图8所示。表5对各测试工况下惯容器输出力仿真值与试验值在一个周期内的均方根值及其误差进行了对比。

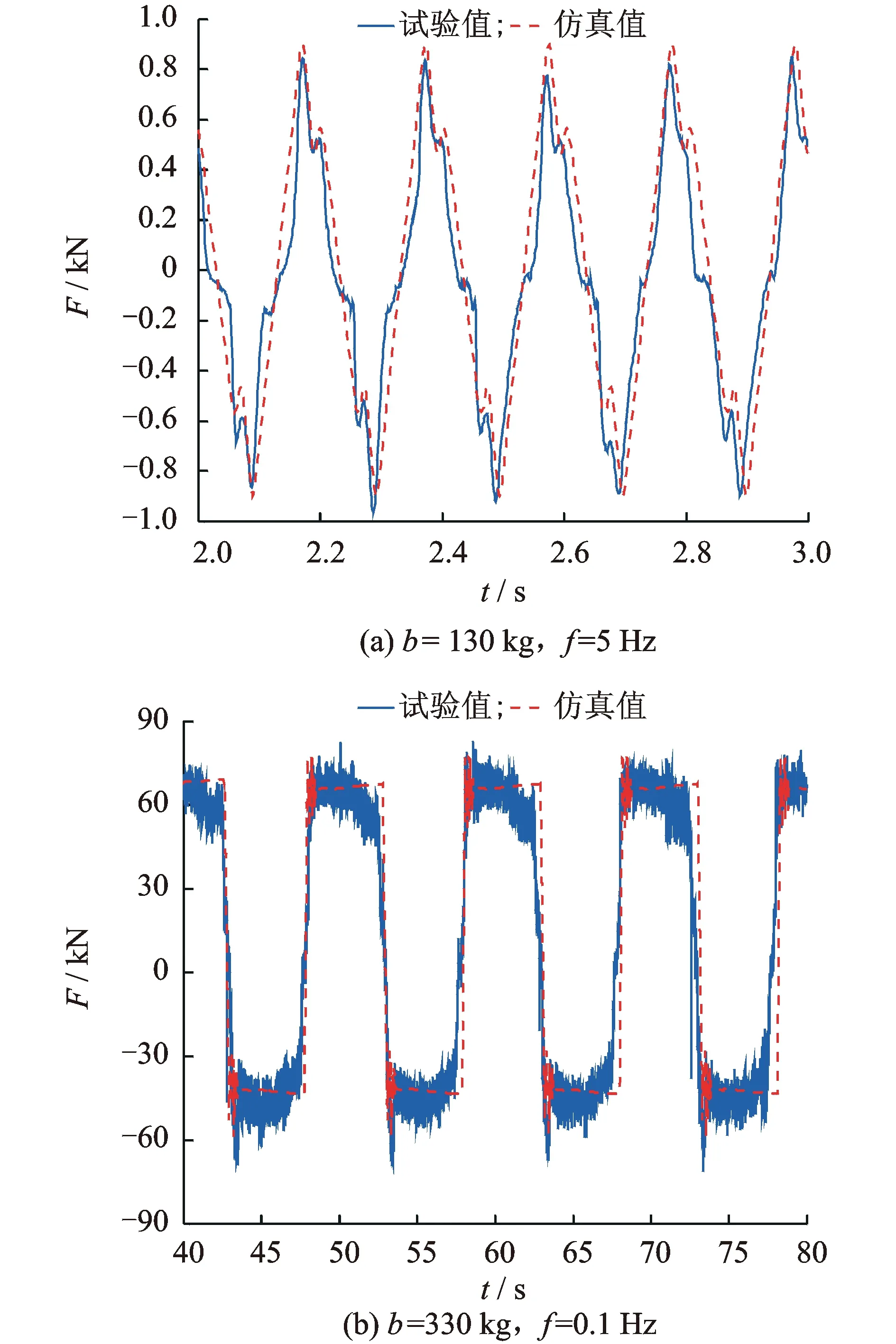
图8　仿真结果与试验结果对比Fig.8　Comparison between simulation results and testing results

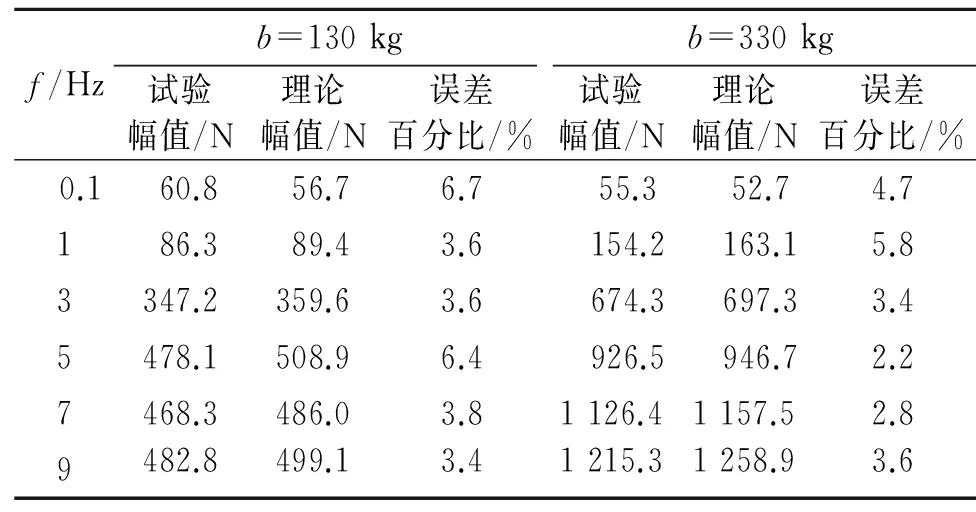
f/Hzb=130kgb=330kg试验幅值/N理论幅值/N误差百分比/%试验幅值/N理论幅值/N误差百分比/% 0.160.856.76.7 55.3 52.74.7186.389.43.6 154.2 163.15.83347.2359.63.6 674.3 697.33.45478.1508.96.4 926.5 946.72.27468.3486.03.81126.41157.52.89482.8499.13.41215.31258.93.6

通过图8及表5可以看出，在不同测试工况下，惯容器输出力的仿真结果与试验结果均吻合良好，同时惯容器输出力在一个周期内的均方根值误差最大不超过7%，平均误差仅为4.2%，模型呈现出良好的拟合精度。模型验证结果表明，通过上述方法得到的惯容器非线性力学模型可以实现惯容器力学性能的有效预测，为进一步分析惯容器非线性对隔振系统性能的影响奠定了良好的基础。

5结束语

笔者建立的包含摩擦、间隙以及丝杠弹性力的惯容器非线性力学模型，能够准确体现出滚珠丝杠式惯容器存在的非线性力学特征。惯容器的力学性能试验结果真实反映了摩擦和间隙对惯容器力学性能的影响，在此基础上，可以对模型中的摩擦和间隙进行合理的简化，从而得到便于参数辨识的模型结构。最小二乘递推算法可以根据试验数据对惯容器力学模型中的参数进行有效辨识，其中，辨识得到的惯容系数与实际值最大误差仅为2.7%，间接验证了该方法的准确性和可靠性。惯容器非线性力学模型的输出力仿真值与试验值在一个周期内的均方根值误差最大不超过7%，平均误差仅为4.2%，说明所建模型以及采用的模型参数辨识方法可以对滚珠丝杠式惯容器非线性力学性能进行有效的预测。

参考文献

[1]Smith M C. Synthesis of mechanical networks: the inerter [J]. IEEE Transactions on Automatic Control，2002，47(10): 1648-1662.

[2]Smith M C，Wang F C. Performance benefits in passive vehicle suspensions employing inerters [J]. Vehicle System Dynamics，2004，42(4)：235-257.

[3]Evangelou S，Limebeer D J N，Sharp R S，et al. Control of motorcycle steering instabilities [J]. IEEE Control Systems Magazine，2006，26(5)：78-88.

[4]Wang Fucheng，Liao Minkai，Liao Bohuai，et al. The performance improvements of train suspension systems with mechanical networks employing inerters [J]. Vehicle System Dynamics，2009，47(7)：805-830.

[5]Jiang J Z，Alejandra Z M，Goodall R M，et al. Passive suspensions incorporating inerters for railway vehicles [J]. Vehicle System Dynamics，2012，50(S)：263-276.

[6]陈龙，张孝良，聂佳梅，等. 基于半车模型的两级串联型ISD悬架性能分析[J]. 机械工程学报，2012，48(6)：102-108.

Chen Long，Zhang Xiaoliang，Nie Jiamei，et al. Performance analysis of two-stage series-connected inerter-spring-damper suspension based on half-car model [J]. Journal of Mechanical Engineering，2012，48(6)：102-108. (in Chinese)

[7]陈龙，杨晓峰，汪若尘，等. 基于二元件ISD结构隔振机理的车辆被动悬架设计与性能研究[J]. 振动与冲击，2013，32(6)：90-95.

Chen Long，Yang Xiaofeng，Wang Ruochen，et al. Design and performance study of vehicle passive suspension based on two-element inerter-spring-damper structure vibration isolation mechanism [J]. Journal of Vibration and Shock， 2013，32(6)：90-95. (in Chinese)

[8]Papageorgiou C，Houghton N E，Smith M C. Experimental testing and analysis of inerter devices [J]. Journal of Dynamic Systems, Measurement, and Control，2009，131(1)：1-11.

[9]Wang Fucheng，Su Weijiun. Impact of inerter nonlinearities on vehicle suspension control [J]. Vehicle System Dynamics，2008，46 (7)：575-595.

[10]Ebrahimi M，Whalley R. Analysis，modeling and simulation of stiffness in machine tool drives [J]. Computer and Industrial Engineering，2000，38(1)：93-105.

[11]唐斌，安西方，何鑫，等. 橡胶钢丝绳复合隔振器动力学建模与参数识别[J]. 振动、测试与诊断，2012，32(5)：746-749.

Tang Bin，An Xifang，He Xin，et al. Dynamic model and parameter identification of rubber and wire-cable composite vibration isolator [J]. Journal of Vibration，Measurement & Diagnosis，2012，32(5)：746-749. (in Chinese)

[12]上官文斌，曾祥坤，刘泰凯，等. 多楔带动态特性及带-轮间摩擦系数的测试分析[J]. 振动、测试与诊断，2013，33(4)：588-596.

Shangguan Wenbin，Zeng Xiangkun，Liu Taikai，et al. Measurement of dynamic properties for serpentine belt and friction coefficient between belt and pulley [J]. Journal of Vibration，Measurement & Diagnosis，2013，33(4)：588-596. (in Chinese)