Hilbert低通滤波器特性分析及改进数值计算方法*

2016-08-03胡异丁任伟新颜健毅

振动、测试与诊断 2016年2期

关键词：截止频率通滤波低通滤波器

胡异丁，　任伟新，　颜健毅，　李　苗

(1.中南大学土木工程学院　长沙，410075) (2.五邑大学信息工程学院　江门，529020) (3.合肥工业大学土木与水利工程学院　合肥，230009)

Hilbert低通滤波器特性分析及改进数值计算方法*

胡异丁1,2，任伟新1,3，颜健毅2，李苗1

(1.中南大学土木工程学院长沙，410075) (2.五邑大学信息工程学院江门，529020) (3.合肥工业大学土木与水利工程学院合肥，230009)

摘要针对基于Hilbert变换的零相位低通滤波器数值计算中，时域离散化带来的频域周期化影响了其低通特性的问题，提出了相应的改进方法。通过证明Hilbert低通滤波器时域解析表达式的频率响应特性，指出离散Hilbert低通滤波器的频响特性混叠了π两侧倒相的频率成分,并根据频响特性图的特征采用两级滤波结构对数值计算方法做出了改进。理论证明了改进后的滤波器能数值实现零相位低通滤波，并通过调幅信号以及调幅-调频信号的仿真算例进行了验证。应变实测信号处理实例表明,改进后滤波器能剔除动应变信号中低频的温度效应成分的影响，适合非平稳信号分析的预处理。

关键词零相位滤波器；解析模式分解； Hilbert低通滤波器；数值计算；非平稳信号处理

引言

在振动信号处理中数字滤波是重要的信号调理手段。数字滤波器在滤波时通常存在相移，其相频特性分为三类：零相位、线性相位和非线性相位[1]。对于平稳信号应用线性相位滤波器信号的相位是不存在失真的，只是有一个延迟。但是振动信号中往往存在非平稳信息，对非平稳信号使用一般滤波器滤波不仅会产生相位失真，还会改变信号的瞬时频率。因此数字信号处理领域引入了零相位数字滤波技术[2-4]。此外，为了避免相位延迟，也可采用信号分解的方式，如经验模态分解或小波分解。文献[5-6]讨论了零相位滤波器在非平稳信号分析中的应用，并将零相位数字滤波器与小波包分解重构和经验模态分解方法的滤波能力进行了比较。

Hilbert变换(Hilbert transform，简称HT)是信号分析与处理中的广泛应用的重要理论工具。最近，Chen等[7]提出了基于Hilbert变换的一种新的信号分解方法——解析模式分解法(analytical mode decomposition，简称AMD)，可从振动时程信号中提取出密集频率的谐波成分，并应用于时变线性和非线性结构系统识别[8]和环境振动结构模态参数识别[9]。Feldman[10]通过改进的Bedrosian公式证明了该分解方法，并对这种方法给出了新的理论解释，认为该算法实际上是一种基于Hilbert变换的低通滤波器，并且具备良好零相位特性，保留了通带内的原始信号的幅度，频率和相位关系，因此适合非平稳信号的滤波。

尽管Feldman给出了滤波器的解析式，但是当采用离散数值计算时，由于时域离散化带来的频域周期化，使得原解析式的计算结果将产生频谱混叠而不能实现低通滤波，因此需要做出改进。

在基于Hilbert变换的零相位低通滤波器的解析证明的基础上，笔者从傅里叶角度证明该滤波器时域解析表达式的频率响应特性；进而发现滤波器解析式的数值计算中存在的问题；在此基础上提出改进的滤波器数值计算方法；采用两个仿真算例比较改进前，后的滤波器特性；最后将其应用到应变实测信号处理的实例中。

1基于Hilbert变换的低通滤波器

Hilbert变换是一种积分变换，信号x(t)的Hilbert变换HT[x(t)][11]定义为

(1)

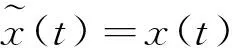
(2)

其中：sgn(Ω)为符号函数；HT(Ω)如图1所示。

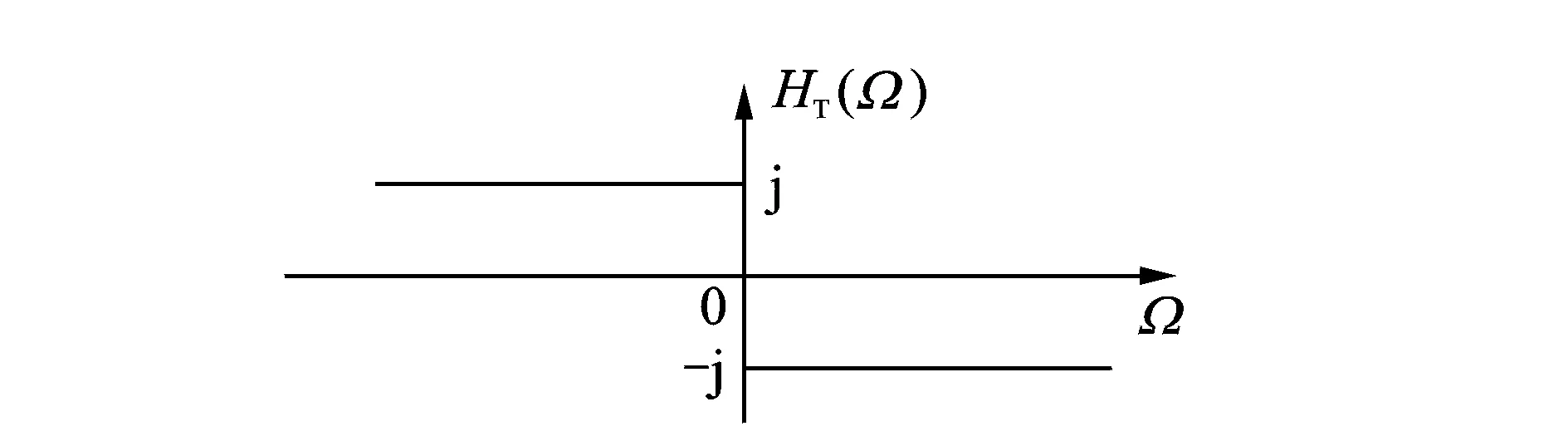
图1　Hilbert变换的频响特性Fig.1　Frequency response characteristic of Hilbert transform

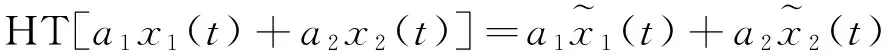
Feldman在Hilbert变换性质及Bedrosian乘积定理[13]的基础上给出了Hilbert低通滤波器的解析证明。

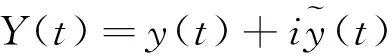
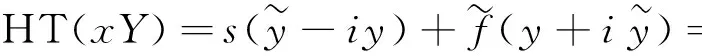
(3)

即可得到

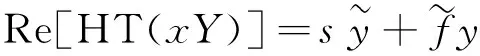
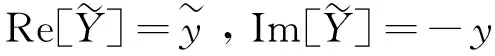
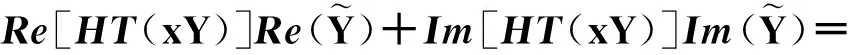
(4)

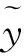
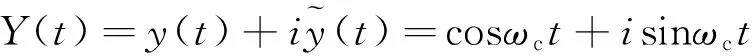
(5)

式(5)表明，任何低于正交函数频率ωc的低频成分s(t)从信号x(t)中被提取出来，因而也可将其理解为基于Hilbert变换的低通滤波器，正交函数的频率ωc也可称为该低通滤波器的截止频率。显然，高于截止频率ωc的高频成分f(t)也可通过f(t)=x(t)-s(t)被分离出来。

2滤波器的频率响应特性证明

考虑输入信号x(t)=s(t)+f(t)，经过式(5)的Hilbert低通滤波器，响应为s(t)，分析该滤波器频率响应特性。

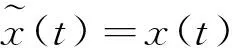
根据傅里叶变换的时域卷积性质和频域卷积性质[14]，求s1(t)的傅里叶变换为

X(Ω)sgn(Ω-ωc)-X(Ω-2ωc)sgn(Ω-ωc)]

其中：X(Ω)为x(t)的傅里叶变换。

同理可求HT[x(t)sinωct]cosωct的傅里叶变换S2(Ω)为

X(Ω)sgn(Ω+ωc)+X(Ω)sgn(Ω-ωc)-

X(Ω-2ωc)sgn(Ω-ωc)]

因此，HT[x(t)cosωct]sinωct-HT[x(t)sinωct]·cosωct的傅里叶变换S(Ω)为

S(Ω)=S1(Ω)-S2(Ω)=

X(Ω)G2ωc(Ω)

(6)

其中

(7)

G2ωc(Ω)为系统频响特性函数，如图2所示。显然，该滤波器相频特性为0，为一零相位理想低通滤波器，截止频率为ωc。

图2　Hilbert低通滤波器频响特性Fig.2　Frequency response characteristic of Hilbert low-pass filter

3数值计算中的问题及改进

3.1数值计算中的混叠和倒相问题

实际工程计算对象往往是数字信号，数据时域的离散化将会带来频域的周期化。因此离散时间信号Hilbert变换器的频响特性为HT(ejω)，这是将图1的HT(Ω)的符号函数周期化，即

(8)

图3　离散Hilbert变换器频响特性Fig.3　Frequency response characteristic of discrete Hilbert transform

离散时间信号Hilbert变换器的频响特性如图3所示，即将图2的符号函数截断且以2π为周期延拓而构成。因此在数值计算中，按照解析式(5)得到的Hilbert低通滤波器频响特性式(7)中的符号函数也将被截断且周期延拓，如图4(a)，(b)所示。假设截止频率ωc<π/2，依据式(7)可得离散时间信号Hilbert低通滤波器的频响特性为G2ωc(ejω)，如图4(c)所示。

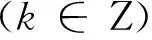
(9)

图4　离散Hilbert低通滤波器频响特性推导过程Fig.4　Derivation process of frequency response characteristic of discrete Hilbert low-pass filter

通过比较图4(c)与图2可知，采用离散时间信号计算Hilbert低通滤波器得到的频率响应,除了保留了ωc以内的低频成分外，还混叠进了π两侧的频率成分，且产生了倒相，因此不再具备低通滤波特性。

例如，设一时长为1s信号x(t)分别由一直流成分和30Hz正弦信号相加，x(t)=2+sin(60πt)，采样率为100Hz。按照式(5)进行数值计算，设截止频率为22Hz，滤波后的成分为s(t)。理论上经过低通滤波后的结果应该仅包含直流成分，而实际计算结果既包含直流成分，又混叠了30Hz信号成分，且产生了倒相，如图5所示。可见大于截止频率22Hz的30Hz正弦信号成分并没有被滤除，而以倒相的形式仍旧存在于滤波后的结果中，计算结果不符合低通特性。

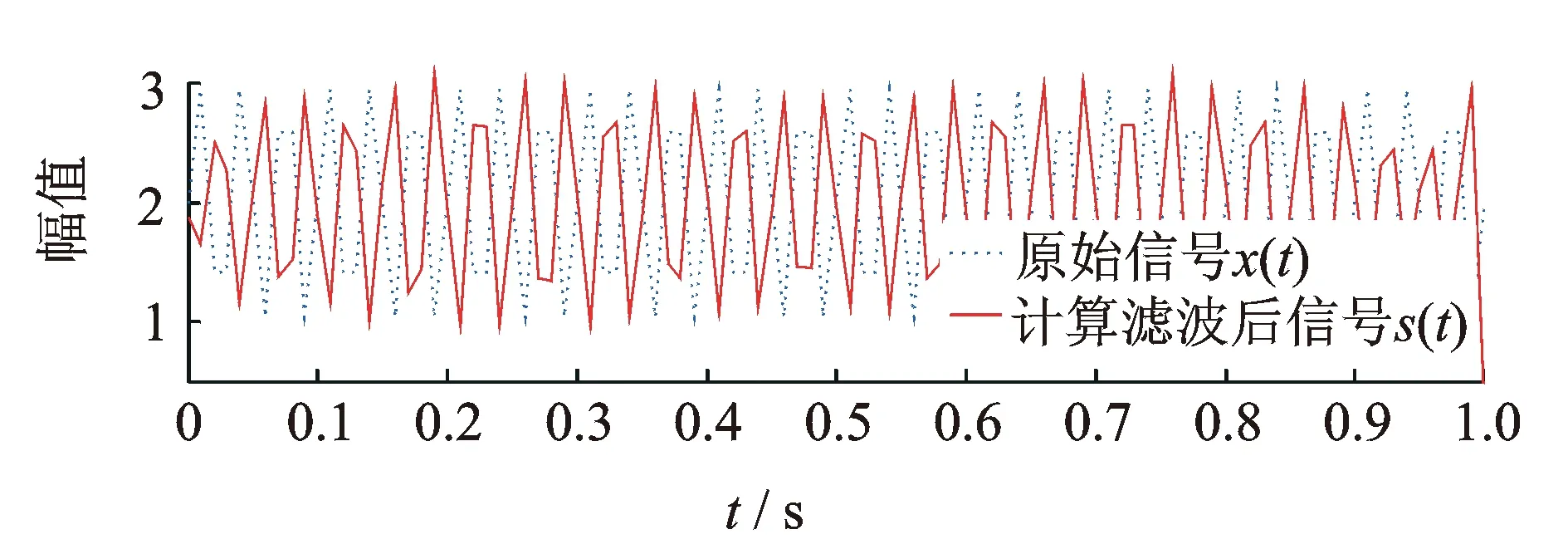
图5　滤波产生倒相示例Fig.5　Example of phase inversion

3.2改进的数值计算方法

(10)

图6　改进的离散Hilbert低通滤波器频响特性Fig.6　Frequency response characteristic of improved discrete Hilbert low-pass filter

综上所述，对一信号x(t)=s(t)+f(t)，其中s(t)为低频成分，f(t)为高频成分，改进的离散Hilbert低通滤波器计算步骤为：

1) 设定合适的滤波器截止频率ωc，将输入信号x(t)除以2，再采用式(5)数值计算得到s′(t)，完成第1级滤波；

2) 将s′(t)做为输入，仍旧设定截止频率为ωc，再经过式(5)数值计算，将计算结果加上s′(t)即得到低频成分信号s(t)，完成第2级滤波。

改进的离散Hilbert低通滤波器结构框图如图7所示，图中虚线框内即式(5)的结构框图。如果数值计算中截止频率ωc>π/2，式(7)中的两个符号函数经周期延拓以后再相减，频响特性仍将发生混叠，不再具备低通特性。因而，实际计算可增大采样频率以保证所需要滤出的低频成分的频率小于π/2。同时，由于工程处理的信号都是有限长度，Hilbert变换数值计算仍旧会产生端点效应[15]。

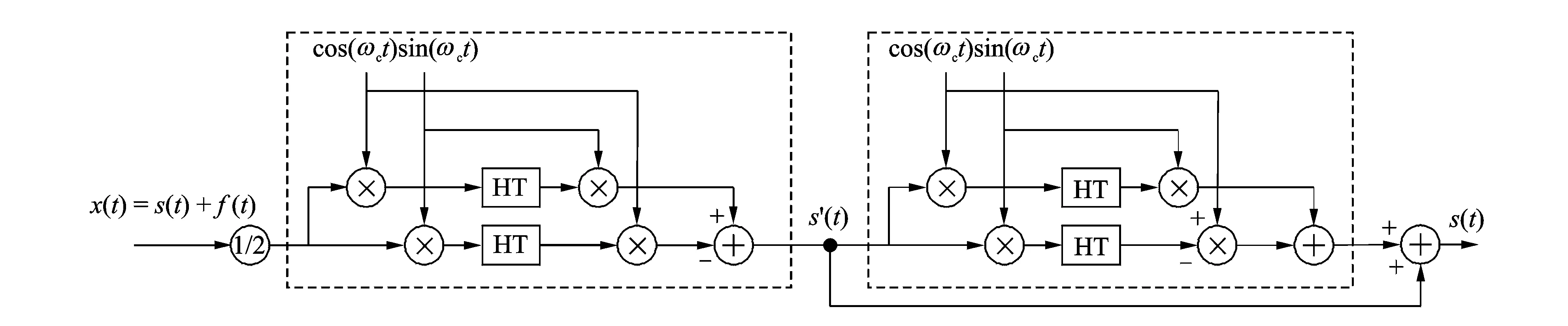
图7　改进的离散Hilbert低通滤波器结构框图Fig.7　Block diagram of improved discrete Hilbert low-pass filter

4仿真算例

4.1算例1

改进前、后的Hilbert滤波器用于处理调幅信号比较。设x(t)为包含两个衰减振荡谐波分量的输入信号，低频分量与高频分量的振荡频率分别为20 Hz和230 Hz，其中低频谐波分量从0.4 s开始，高频谐波分量从0.2 s开始，数值表达式如下

其中：u(t)为阶跃函数。

设置低通截止频率为50 Hz，分别用改进前、后的Hilbert滤波器对输入信号x(t)进行数字滤波。信号x(t)波形如图8(a)所示。信号经数值离散化，采样率为500 Hz。改进前Hilbert滤波器输出的既有20 Hz分量又有倒相以后的230 Hz的分量，没有完成低通滤波任务，结果如图8(b)所示。改进后Hilbert滤波器输出仅有20 Hz分量，结果与原有信号低频成分的幅度、相位一致，正确实现了零相位低通滤波任务，结果如图8(c)所示。需注意改进后滤波器输出信号原信号中,低频20 Hz成分的x1(t)，在信号发生突变的位置(0.4 s处)产生了一定的失真，这是因为突变点的存在类似于将信号在该点截断，引入了新的端点。

图8　算例1的改进前、后滤波结果比较Fig.8　Comparison of results of the filter before and after improvement in the first example

4.2算例2

改进前、后的Hilbert滤波器用于处理调幅-调频信号比较。设x3(t)为1 s内瞬时频率从5 Hz变到200 Hz的线性调频信号；x4(t)=sin(4πt)，为慢变2 Hz正弦信号；输入信号为x(t)=x3(t)·x4(t)。信号经数值离散化，采样频率为400 Hz。

设置Hilbert低通滤波器截止频率为100 Hz，分别用改进前、后的Hilbert滤波器进行数字滤波得到结果分别如图9(a)和(b)所示。从图9(a)中可看到，改进前滤波结果在0.5 s以后仍有输出，即信号大于截止频率100 Hz的成分仍旧存在，因此未能正确实现低通滤波效果。图9(b)中，改进后滤波结果在t<0.5 s内与输入信号幅度相位都一致，而当t>0.5 s信号基本为零，表明滤除大于截止频率100 Hz的成分，正确实现了低通滤波效果，且具备优越的零相位特性，能有效消除滤波环节中对通带内信号造成的相位失真和瞬时频率的改变。因此该滤波方法可广泛应用于桥梁振动，地震波等非平稳信号分析的预处理中。

图9　算例2的改进前、后滤波结果比较Fig.9　Comparison of results of the filter before and after improvement in the second example

5实测信号处理实例

健康监测系统所监测到的动态应变除了交通荷载影响外，还包括有环境(温度等)的影响，因此通常采用温度补偿片贴在与构件相同的材料上进行温度补偿。对于大跨度桥梁结构，特别是悬索桥、斜拉桥等多次超静定结构系统，温度对结构动力特性的影响与桥梁边界约束条件有显著关联，从而对结构的应力状态具有较大的影响[16-17]。而温度补偿片仅剔除了电阻应变片箔丝材料本身的温度应变，补偿后动应变信号仍具有与温度变化相关的波动形式，正是反映的结构温度应力作用，为典型的非平稳信号。

笔者分析的实测动应变信号采自坝陵河悬索桥。根据大桥所在地的天气情况，选择在温度波动较大的季节(4月份)对钢桁架杆件的应变进行测量，应变测试的测点位于桥梁主跨的跨中节段。图10为跨中钢桁梁上游上弦杆测点一天应变测量数据，采集仪器为HBM MGCplus AB22A，数据已做温度补偿，采样率为50 Hz。

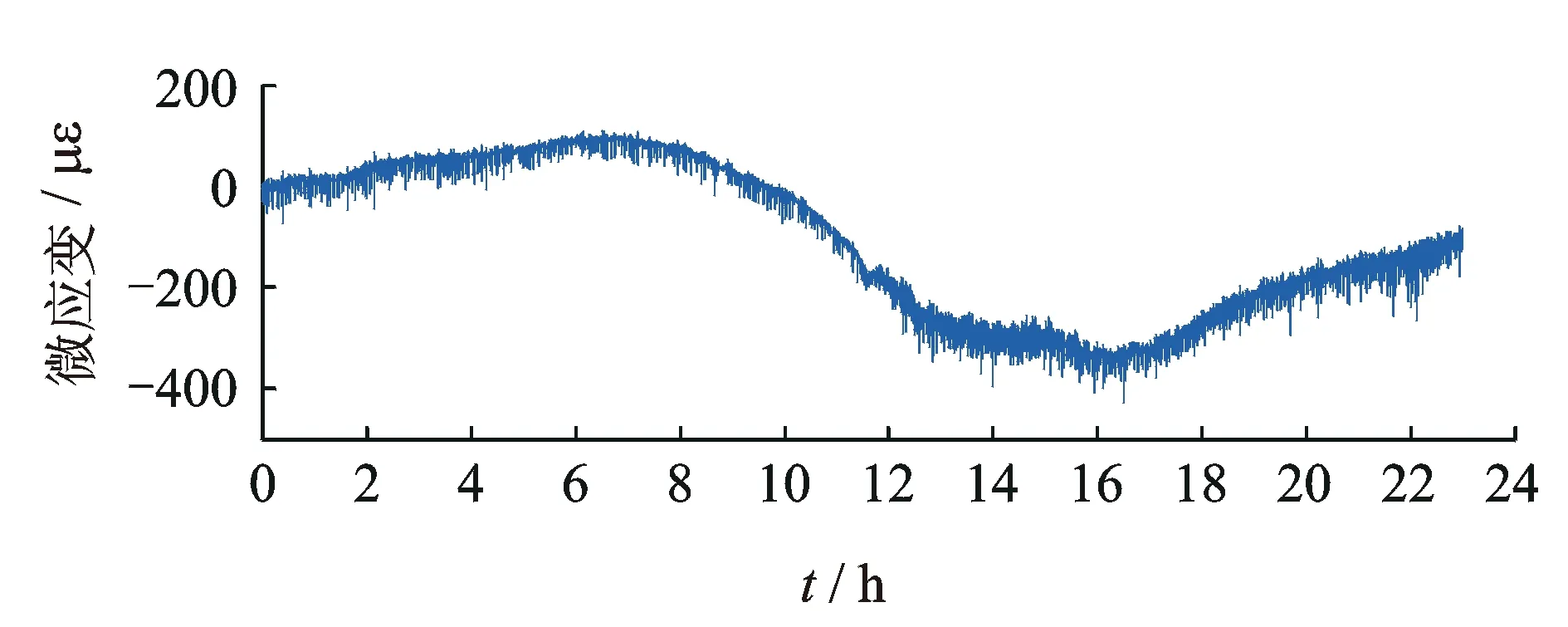
图10　温度补偿后的应变时程Fig.10　Temperature-compensated strain history

图11　Hilbert低通滤波处理后的温度效应成分和动荷载应变时程Fig.11　Temperature effect component and strain history of dynamical load processed with Hilbert low-pass filter

因为处理的数据对象是非平稳数字信号，采用笔者改进的Hilbert低通滤波器处理数据，其零相位特性将不会改变滤波后数据的相位和瞬时频率特征，以保证非平稳信号处理的正确性。由于温度效应变化频率极慢的特征，其低通特性则可以提取温度变化的慢变趋势。设置截止频率为0.005 Hz，滤出的结构动态应变信号中的温度效应成分如图11(a)所示，图中慢变的低频成分反映了结构温度应力所产生的应变时程。剩余的成分主要为动荷载产生的应变时程如图11(b)所示，这对由车辆荷载引起的桥梁结构损伤识别，移动车辆识别等具有重要意义。可见，改进Hilbert低通滤波器能应用于实测非平稳信号的预处理中。

6结束语

将基于Hilbert变换的零相位低通滤波器应用到非平稳信号分析中，并从傅里叶变换角度证明了该滤波器零相位低通频率响应特性。由于数值计算中符号函数频域上的周期延拓，使得Hilbert变换低通滤波器原解析式低通带宽特性在π两侧发生改变，在此基础上提出了两级滤波结构的改进滤波器数值计算方法。两个仿真算例验证改进后的滤波器才能正确完成零相位低通滤波。应变测量数据处理实例表明，该滤波器能剔除动应变信号中低频的温度效应成分的影响，适合非平稳信号分析的预处理。

参考文献

[1]Smith S W. The scientist and engineer′s guide to digital signal processing[M].2nd ed. San Diego: California Technical Publishing, 1999:328.

[2]Gustafsson F. Determining the initial states in forward backward filtering [J].IEEE Transactions on Signal Processing, 1996,44(4): 988-992.

[3]纪跃波,秦树人,汤宝平.零相位数字滤波的方法与实现[J] .振动、测试与诊断, 2000,30(S1):167-172.

Ji Yuebo, Qin Shuren, Tang Baoping. Digital filtering with zero phase error method and implementation[J]. Journal of Vibration， Measurement & Diagnosis, 2000,30(S1): 167-172. (in Chinese)

[4]吴国乔,王兆华.基于全相位的零相位数字滤波器的设计方法[J]. 电子与信息学报，2007,29(3):574-577.

Wu Guoqiao, Wang Zhaohua. Design method of digital filter with zero-phase based on all phase[J]. Journal of Electronics & Information Technology, 2007, 29(3):574-577. (in Chinese)

[5]李之雄,郭瑜,郑华文.零相位滤波器在非平稳信号分析中的应用研究[J].昆明理工大学学报:理工版,2007, 32(5):18-22.

Li Zhixiong, Guo Yu, Zheng Huawen. Study on the application of zero-phase filter to non-stationary signal analysis[J]. Journal of Kunming University of Science and Technology: Science and Technology, 2007, 32(5):18-22. (in Chinese)

[6]常广,鄢素云,王毅.零相位数字滤波器在非平稳信号处理中的应用[J].北京交通大学学报,2011,35(6): 49-56.

Chang Guang, Yan Suyun, Wang Yi. Application of zero-phase digital filter on non-stationary signal processing[J]. Journal of Beijing Jiaotong University, 2011,35(6): 49-56. (in Chinese)

[7]Chen Genda, Wang Zuocai. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components [J]. Mechanical Systems and Signal Processing, 2012, 28: 258-279.

[8]Wang Zuocai, Ren Weixin, Chen Genda. Time-varying linear and nonlinear structural identification with analytical mode decomposition and Hilbert transform[J]. Journal of Structural Engineering, 2013, 139(12): 06013001.

[9]Wang Zuocai, Chen Genda. Analytical mode decomposition with Hilbert transform for modal parameter identification of buildings under ambient vibration[J]. Engineering Structures, 2014, 59:173-184.

[10]Feldman M. A signal decomposition or lowpass filtering with Hilbert transform[J]. Mechanical Systems and Signal Processing, 2011, 25(8): 3205-3208.

[11]胡广书. 数字信号处理-理论、算法与实现[M].2版.北京：清华大学出版社，2003:157.

[12]Feldman M. Hilbert transform in vibration analysis [J]. Mechanical Systems and Signal Processing, 2011, 25(3):735-802.

[13]Bedrosian E. A product theorem for Hilbert transform [J]. Proceedings of the IEEE, 1963, 51: 868-869.

[14]郑君里,应启珩,杨为理. 信号与系统:上册[M].2版. 北京:高等教育出版社, 2000:138-143.

[15]Feldman M. Hilbert transform applications in mechanical vibration [M]. United Kingdom: John Wiley & Sons, 2011:56-58.

[16]许永吉,朱三凡,宗周红．环境温度对桥梁结构动力特性影响的试验研究[J]．地震工程与工程振动，2007, 27(6):119-123.

Xu Yongji, Zhu Sanfan, Zong Zhouhong. Experimental study on effects of environmental temperature on dynamic characteristics of bridge structures[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(6):119-123. (in Chinese)

[17]Ni Yiqing, Hua Xugang, Fan Keqing, et al. Correlating modal properties with temperature using long-term monitoring data and support vector machine technique[J]. Engineering Structures, 2005, 27(12):1762-1773.