装备故障测试方案优化的概率截止算法*

2016-08-03吕建伟谢宗仁

振动、测试与诊断 2016年2期

关键词：武器装备优化方案

吕建伟，　谢宗仁，　狄　鹏

(海军工程大学管理工程系　武汉，430033)

装备故障测试方案优化的概率截止算法*

吕建伟，谢宗仁，狄鹏

(海军工程大学管理工程系武汉，430033)

摘要在装备研制的早期阶段，需要及时将装备的测试性指标和故障测试方案联系起来，并对测试方案进行优化。针对这些要求，首先，对常规故障模式、影响及危害性分析(failure mode effects criticality analysis,简称FMECA)的不足之处，提出了对于FMECA故障模式的输入信息进行改进的设想和实施方法；然后，根据研究需求探讨并确定了故障的检测特性影响指标，分别给出了各特性指标的影响等级、影响值的确定方法；最后，建立了装备故障的检测特性指标综合评估模型，提出了测试方案的优化截止算法，采用典型示例对其进行了计算验证，并对其应用进行了深入探讨。结果表明，该方法能够有效弥补现有设计方式的不足，为在研制早期制订装备测试优化方案提供了理论依据。

关键词武器装备；故障检测特性；研制早期；测试性；优化方案

引言

在装备研制过程中，当人们通过作战需求分析、系统结构分析和类比分析等方式，提出了系统设备的测试性需求指标[1-2]之后，在技术上就应该采取相应的测试性设计措施，来确保各系统设备的设计结果能够达到这些测试性指标，而且应在装备研制早期(例如方案阶段)，在确定装备测试方案的时候，就能够知道所采取的设计措施，能否保证达到规定的测试性指标。从指标要求的角度看，概率型的测试性指标一般很少要求达到100%，一般都在80%～98%之间，这就说明，允许对于某些故障不采取诊断措施(允许漏检)；从装备故障的角度来看，不是每一个故障都“值得”或“能够”采用机内测试(built in test,简称BIT)等手段去诊断(检测+定位+隔离)的。例如：某类故障采用人工方式很容易发现和判别[3]；某类故障发生的概率非常低；某类故障的后果影响较为轻微等。

综上所述，在测试性设计中，人们所采取的设计措施，既要达到规定的测试性指标要求，还要以较低的代价达到要求，在选择测试方案时，还要对装备的故障有所取舍，在研制早期如何做到这一点，是一个很有价值的问题。目前，有的将其称为“诊断方案的制订[4]”，有的将其称为“测试方案的优化[5-6]”，但是均不能完全满足以上要求。例如，有的只能适应装备的详细设计阶段[7-10]，有的对装备故障的取舍没有考虑到其本身的特性[11-12]等。笔者就此问题给出一种基于改进的FMECA的概率截止算法。

1常规的FMECA方法及其分析

FMECA是针对装备所有可能的故障，确定每种故障模式对装备各层次的影响，按故障后果的严酷度及其发生概率确定其危害性。常规的FMECA包括故障模式及影响分析(failure mode effects analysis,简称FMEA)和危害性分析(criticality analysis,简称CA)，见表1所示。

常规FMECA的实施可以划分为如下步骤。

1) 相关的准备工作。包括掌握装备结构和功能的有关资料，收集装备的使用、维修和环境条件等信息；定义装备及其功能和最低工作要求；同时根据需要来确定分析级别，即约定的分析层次。

2) 找出装备的故障模式，分析其原因及影响。

3) 确定装备故障的相关属性。包括确定故障的检测方法，找出可能的补偿措施，用定性或定量的形式确定故障模式危害的严酷程度以及对应的概率等级。按照表1或类似的格式填写FMECA表，并生成危害性矩阵等。

表1　故障模式影响及危害性分析(FMECA)工作表

Tab.1　Failure mode effects and criticality analysis (FMECA) working sheet

初始约定层次___________ 阶段________约定层次_______第____页共___页

代码产品标号或元器件位号功能故障模式故障原因故障影响局部影响高一层次影响最终影响故障检测方法补偿措施严酷度类别概率等级

分析人员__________ 审核_________ 批准_________ 填表日期__________

在实际工作中，如需要进行定量FMECA，则需填写CA表；如果仅进行FMEA，则确定概率等级和生成危害性矩阵工作就不必进行。常规的FMECA是一种适应面很广且在装备研制中广泛使用的工具，但就目前的使用结果而言，存在着形式化等不足之处，同时所能够提供的信息有限，现作具体分析。

2故障模式的输入信息来源和种类

要确定装备的测试方案进而开展测试性设计，FMECA是其中不可缺少的环节。但是在实际工作中，开展FMECA分析是一项看似简单、实则很难做好的工作，不仅需要具备较为丰富的工程经验，还要求掌握装备的工作原理和使用、维修情况，其中最重要的是找出产品的故障模式。以往人们进行FMECA分析时，主要是依赖分析人员自身的努力，借助经验和对装备的工作原理的掌握来完成对应的分析，这样就容易产生很多问题，如系统和设备的层次划分不当、忽视和遗漏某些故障、所提出的故障模式过于粗陋且没有针对性等，导致往往只是形式上完成了这项工作，失去或降低了进行FMECA分析对设计工作的指导意义。

笔者在进行了广泛深入的分析以后认为，在进行装备FMECA分析时，其故障模式的输入形式应从“基于经验和理论知识的分析”转变为“基于同类型装备以往的故障记录的分析”，以此形成FMECA的初始输入，在分析中还必须有效扩展所提供的故障信息，才能够有效地提高分析质量，并使分析结果满足装备测试性设计的需求。

在装备论证阶段，应广泛收集同类装备以往所发生的尽可能多的故障类型以及相关的较为详细的原始信息，从中提取、归纳所需要的导出信息。

首先，完成常规的FMECA分析所需要的信息，如表1中所需的故障模式的严酷度和发生概率等，这些已是常规的工作；其次，为了满足面向故障的装备测试性设计的需要，还需要考虑、评估某个故障在技术上是否易于实现对故障进行诊断，即实现诊断的技术难易程度[3]，以及对应的人工诊断故障的难易程度，这两个指标涉及到对装备进行测试性设计的成本问题。为了提取这些信息并使之量化，需要分析人员、产品设计人员与使用人员共同努力，使原始故障信息中的定性描述变为定量评估结果；在以上工作的基础上，考虑到面向故障的测试性设计的效益问题，还必须考虑对装备各类故障进行修复的时间性指标，例如平均故障修复时间(mean time to repair，简称MTTR)的绝对值大小，以及故障诊断时间在MTTR中的相对占比等因素。

以上各指标分别涉及到FMECA所提供的常规信息、测试性设计的成本和测试性设计，包括了故障模式的5个属性，指标之间相互独立，构成了面向故障的测试性设计所需的完备信息，这里将其通称为故障的检测特性指标，见图1。

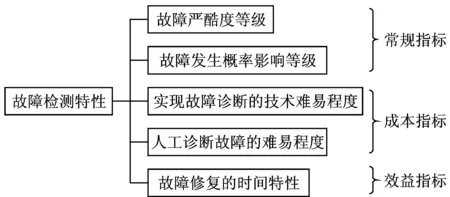
图1　装备故障的检测特性指标Fig.1　Equipment failure test characteristics

与此相对应，在装备的方案阶段，应对系统设备承制方做进一步调研，通过新一轮的FMECA分析，预测新研制装备可能发生的故障，对论证阶段确定的故障模式进行修正，排除其中不大可能出现的故障，加入新预测到的故障，并分析得到新故障的检测特性指标。完成了以上工作，就可以对下面的建模和优化计算提供可靠有效的输入。

3故障的检测特性指标及其影响值

根据以上分析，故障的检测特性指标包括故障严酷度等级、概率影响等级、实现测试的技术难易程度、人工诊断故障的难易程度以及故障修复的时间特性等5类。为便于评估和优化计算，这里将其影响值统一划分为5个影响等级。

1) 故障严酷度等级。故障严酷度一般定义为故障模式所产生后果的严重程度，包括灾难故障、致命故障、临界故障、轻度故障和轻微故障等。与严酷度影响等级“Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ”相对应，严酷度影响值fi1(i为装备故障编号，下同)分别取为“5，4，3，2，1”。具体定义和等级划分如表2所示。

表2　故障严酷度影响等级的定义和划分

Tab.2　Definitions and grades about failure severity

严酷度类别影响等级影响值严酷程度的说明灾难故障Ⅰ5会引起人员死亡或系统损坏的故障致命故障Ⅱ4会引起人员严重伤害,重大经济损失,导致任务失败的系统严重损坏的故障临界故障Ⅲ3会引起人员轻度伤害,一定的经济损失,或导致任务延误或降级的系统严重损坏的故障轻度故障Ⅳ2一种不足以导致人员伤害,经济损失较小,但会导致非计划维修的故障轻微故障Ⅴ1不影响完成规定功能,无需排除或可轻易排除的故障

2) 故障发生概率影响等级。其概率影响等级fi2反映了故障发生概率的大小。这里设故障发生概率影响等级Ⅰ级最高，故障发生概率影响等级越高，相应地对测试性的要求也越高，故障模式发生概率特征及其影响等级如表3所示。

表3　故障发生概率影响等级的定义和划分

Tab.3　Definitions andgrades about failure probability

发生概率特征影响等级影响值发生概率的说明参考概率pi2高概率Ⅰ5经常发生>0.20中等概率Ⅱ4有时发生0.10～0.20不常发生Ⅲ3偶然发生0.01～0.10不大可能发生Ⅳ2很少发生0.001～0.010近乎为零Ⅴ1极少发生<0.001

影响等级和影响值是一种为了便于进行评估计算的表达方式。同时，为了考虑和计算设计措施与测试性指标之间的定量关系，表中最后一列采用GJB1391-2006中的范围，给出了相应等级的参考概率pi2(i为故障编号)，在收集数据时，最好能收集齐全所需信息，以便从统计数据中计算得到该指标，否则也可采用经过广泛核实的估计数值。

3) 实现故障诊断的技术难易程度[3]。其技术难易程度fi3是指在技术上达到预定的故障诊断目标(例如设置检测点或电路)的难度。确定该指标一般要综合考虑故障部位、装备的性质和诊断技术的最新发展等因素。

实现故障诊断的技术难易程度影响等级Ⅰ级为最高，该指标等级越高，相应地对测试性的要求也就越高，实现故障诊断的技术难易程度的5个影响等级见表4。

表4　实现故障诊断的技术难易程度影响等级定义和划分

Tab.4Definitions andgrades about technical difficulty degree of failure diagnosis

实现故障诊断难易程度影响等级影响值实现故障诊断的技术难易程度的定义很容易Ⅰ5很容易实现测试性设计容易Ⅱ4较容易实现测试性设计一般Ⅲ3一般能实现测试性设计较难Ⅳ2较难实现测试性设计很难Ⅴ1很难实现测试性设计

4) 人工诊断故障的难易程度。这里指的是采用人工的形式，通过使用人员的感官意识到或发现故障，并较易进行故障定位、隔离的难易程度。其程度影响等级Ⅰ级为最高，人工诊断故障的难易程度等级越高，相应地对测试性设计的要求也越高，难易程度fi4的5个影响等级见表5。

表5　人工诊断故障的难易程度影响等级的定义和划分

Tab.5Definitions andgrades about difficulty degree of failure diagnosis by manual acting

人工诊断故障的难易程度影响等级影响值人工诊断故障的难易程度的定义很难Ⅰ5很难进行人工故障诊断较难Ⅱ4较难进行人工故障诊断一般Ⅲ3一般能实现人工诊断容易Ⅳ2容易能实现人工诊断很容易Ⅴ1很容易实现人工诊断

5) 故障修复的时间特性。在GJB451A-2005中，故障平均修复时间定义为产品维修性的一种基本参数，它是一种设计参数。从故障诊断和装备修复的角度来看，可以将故障修复的时间特性归结为两个方面：a.故障平均修复时间(MTTR)的绝对值大小;b.故障诊断(检测、隔离)时间在MTTR中所占的百分比[3]。因此，MTTR越长，故障检测、隔离时间在MTTR中所占的百分比越大，则平均故障修复时间对测试性要求的影响也就越大，相应地进行测试性设计的效益也就越高。为与前面的指标评估值统一起见，综合MTTR大小和故障诊断时间所占百分比这两个方面的特性，将故障修复的时间特性fi5指标仍分为5个影响等级，见表6。

表6　故障修复的时间特性影响等级的定义和划分

Tab.6Definitions andgrades about time characteristics of failure repair

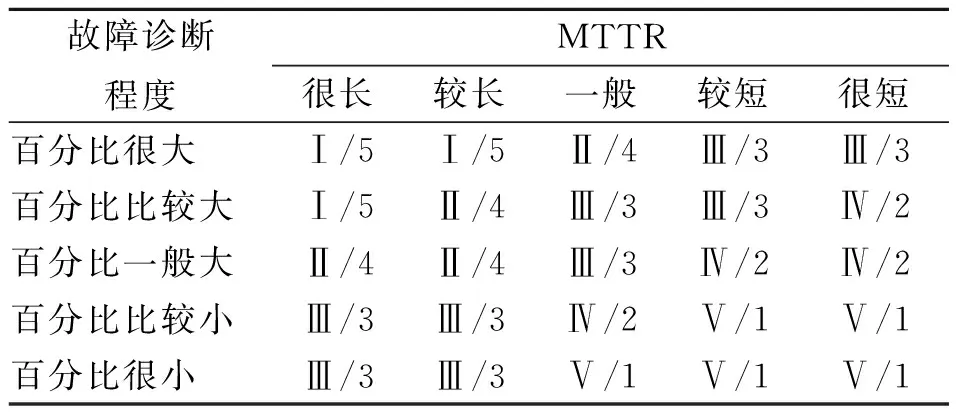
故障诊断程度MTTR很长较长一般较短很短百分比很大Ⅰ/5Ⅰ/5Ⅱ/4Ⅲ/3Ⅲ/3百分比比较大Ⅰ/5Ⅱ/4Ⅲ/3Ⅲ/3Ⅳ/2百分比一般大Ⅱ/4Ⅱ/4Ⅲ/3Ⅳ/2Ⅳ/2百分比比较小Ⅲ/3Ⅲ/3Ⅳ/2Ⅴ/1Ⅴ/1百分比很小Ⅲ/3Ⅲ/3Ⅴ/1Ⅴ/1Ⅴ/1

在表6中，与“Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ”相对应的影响值取值分别为“5，4，3，2，1”。

4装备故障的检测特性综合评估和测试性设计的优化算法

这里以故障检测率PD为例给出优化算法。以X={x1,x2,…,xn}表示装备的故障特性模式集，其中n为故障模式的数量，则有xi=(fi1,fi2,fi3,fi4,fi5)。以F(xi)表示故障模式的检测特性综合指标，将其定义为

(1)

根据所收集的导出信息按照表2～6进行评估，可得到各故障模式i(i=1, 2, …,n)的单项特性影响值fij(j=1,…,5)，同时根据相关信息得到每个故障模式发生的参考概率pi2。

(2)

则表明应以标号m为截止点，标号≤m以前的所有故障模式都必须采用测试性设计措施而实现故障诊断。

由于式(1)综合考虑了故障模式的严酷度、发生概率、实现测试的技术难易程度、人工诊断故障的难易程度以及故障修复的时间特性，用这种方法选出的待检测故障，是综合考虑了以上因素而要求进行测试性设计的，这就可以确保“能够、值得而且必须”检测的故障能够入选，其特性一般包括：故障后果较为严重-故障发生较为频繁-检测的技术难度不大-人工检测困难-故障的时间特性使得技术检测的效益较高；而具有相反特征的故障，在式(2)成立的前提条件下则会被舍弃。

5优化计算示例和结果分析

表7某系统故障模式信息与评估结果

Tab.7The information and evaluation sheet to a system’s failure modes

故障序号fi1fi2fi3fi4fi5F(xi)pi2pm15453412000.1730.1732434447680.0900.2633343434320.1820.4454435233600.0900.5355342533600.1600.6956425322400.0080.7037532321800.0700.7738533221800.0800.8539233331620.0700.92310233421440.0600.98311324231440.0080.9911232422960.0091.000

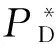
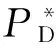
6结束语

在装备测试性设计工作中，当人们通过作战需求分析、系统结构分析和类比分析等方式，提出了系统设备的测试性需求指标之后，下一步的重要工作就是确定装备的故障诊断方案。对于在装备研制早期(包括论证和方案阶段)所确定的故障诊断方案有很多方面的要求，包括能够满足规定的指标要求，能够明确设计措施和所规定指标的一一对应关系，允许忽略和放弃一部分故障(不采取设计措施)并以较低的代价实现故障诊断方案等，笔者所提出的优化算法能够较好地解决以上问题。和常规方法相比，该算法思路清晰，针对性较强，计算简洁明了，有效弥补了现有方法的不足。同时，如果原始数据较为可靠，采用这种算法可以精确计算截止累计概率，能够确保设计结果以较低的成本达到规定的测试性指标，从而可以有效指导装备研制早期的测试性优化方案的制订。

参考文献

[1]张延生, 黄考利, 陈建辉. 复杂装备测试性指标确定方法研究[J].军械工程学院学报, 2010, 22(6): 7-10.

Zhang Yansheng, Huang Kaoli, Chen Jianhui. Research on determining TFOMs of complex equipment [J]. Journal of Ordnance Engineering College, 2010, 22(6): 7-10. (in Chinese)

[2]Su Yongding, Qiu Jing. Modeling of testability requirement based generalized stochastic petri nets[J].Journal of China Ordnance, 2009,5(1): 60-64.

[3]陈春良, 王森.典型装甲车辆测试性要求确定及验证研究[R].北京: 装甲兵工程学院, 2008.

[4]石君友.测试性设计分析与验证[M].北京：国防工业出版社, 2011: 94-97.

[5]陈希祥, 邱静, 刘冠军.测试不确定条件下基于贝叶斯网络的装备测试优化选择技术[J].中国机械工程, 2011, 22(4): 379-384.

Chen Xixiang, Qiu Jing, Liu Guanjun. Optimal test selection of materiel based on bayesian network under test uncertainty[J].China Mechanical Engineering, 2011, 22(4): 379-384. (in Chinese)

[6]黄鑫, 连光耀, 常天庆, 等.基于技术成熟度和二进制粒子群优化算法的装备测试优化方法研究[J].兵工学报, 2011, 32(9): 1171-1176.

Huang Xin, Lian Guangyao, Chang Tianqing, et al. Study on optimization method based on technology readiness assessment and binary particle swarm optimization for equipment test design[J].Acta Armamentarii,2011, 32(9): 1171-1176. (in Chinese)

[7]Francesca G, Antonio V, Enrico N, et al. Modelling and solving optimal placement problems in wireless sensor networks[J]. Applied Mathematical Modeling, 2011, 35(1): 230-241.

[8]Edward M, Kevin M, Jonathan N. Optimized sensor placement for damage parameter estimation[J]. Structural Health Monitoring, 2013, 12(3): 197-206.

[9]吴定海, 张培林, 任国全, 等.发动机异常检测多目标优化方法[J].振动、测试与诊断, 2013, 33(2): 214-218.

Wu Dinghai, Zhang Peilin, Ren Guoquan, et al. Multi-objective optimization of diesel engine abnormal detection[J].Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 214-218. (in Chinese)

[10]朱喜华, 李颖晖, 侯世芳, 等. 考虑传感器故障检测能力的PHM系统传感器优化配置方法[J]. 宇航学报, 2013, 34(9): 1253-1258.

Zhu Xihua, Li Yinghui, Hou Shifang, et al. Sensor optimization placement method for PHM system taking the fault detectability of the sensor into account[J]. Journal of Astronautics, 2013, 34(9): 1253-1258. (in Chinese)

[11]Liu Ying, Ma Hailiang, Zhou Fangjun. Optimization of test points at circuit board based on network topology structure[J]. Advances in Intelligent and Soft Computing, 2012, 169(2): 507-511.

[12]Sen Deng, Bo Jing, Zhou Yang. Test point selection strategy under unreliable test based on heuristic particle swarm optimization algorithm[C]∥Proceedings of IEEE 2012 Prognostics and System Health Management Conference. Beijing，China:IEEE Reliability Society，2012:1-6.